DeepSeek-R1技术剖析：没有强化学习基础也能看懂的PPO & GRPO

©PaperWeekly 原创 · 作者 | 张逸骅

单位 | 密歇根州立大学博士生

研究方向 | 可信人工智能

开篇

在强化学习（RL）中，如果我们只知道“做对了能拿多少分”，那往往还不够，因为单纯追求高分可能带来种种副作用，比如过度搜索、模型不稳定、甚至“走捷径”而偏离合理范围。

为了解决这些问题，人们在 RL 中设计了许多机制——Critic（价值函数）、Clip 操作、Reference Model、以及最近流行的 GRPO（Group Relative Policy Optimization）等。

为了把这些概念讲得更生动，我们不妨打个比方：把 RL 模型的训练过程想象成小学里的考试场景。我们（被训练的模型）就像努力考高分的学生，发奖品的人则像 Critic 或者其他调控机制。接下来就让我们循序渐进地看看，为什么只靠最终成绩是不够的，为什么需要一步步引入 Critic、Clip、Reference Model，最后又是如何引出 GRPO 的思路。

只有Reward时的朴素做法：为什么会有问题

假设我和我弟弟都在小学同一个班上课。老师改卷后给出一个“绝对分数”，我的成绩一般 80 分以上，弟弟成绩大概 30 分左右。然后我们把这个分数直接拿去找爸爸要零花钱——也就是用“分数本身”作为奖励（Reward）。谁考得分数高，零花钱就多。

一开始听上去没毛病，但结果就有两个问题：

• 不公平：如果弟弟从 30 分进步到 60 分，付出了非常大的努力，却依然比不过我平时随便考个 80+。他得不到有效激励。
• 不稳定：我为了冲刺高分，可能会采取极端学习策略（比如疯狂刷题、考前通宵），偶尔考到 95 分，偶尔只有 60 分，成绩大起大落，导致奖励信号也忽上忽下。

这样一来，只拿绝对分数当作 Reward，奖励信号波动很大，弟弟也会觉得不公平，久而久之，就没动力进步了。

数学对应

在强化学习里，如果我们只用：

也就是“把最终 Reward 直接拿来做优化目标”，就容易出现高方差、激励不充分等问题。换言之，Actor 得不到一个和自身水平相称的参考线（baseline），进而影响学习效率。

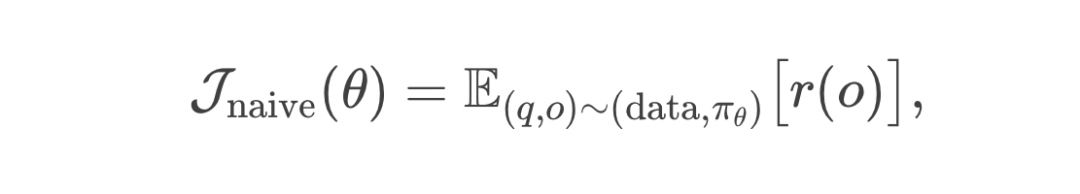
引入 Critic：用“预期分数线”来改善奖励机制

针对上面的问题，爸爸很快意识到：“不能光看绝对分，而要看看每个人在自己水平线之上进步多少才是关键。”

于是爸爸决定：

• 给我定一个“预期分数线” 80 分；给弟弟定一个“预期分数线” 40 分。考试时，只要超出自己那条线，就能得到更多零花钱；如果没有超出，那么零花钱就可能很少或者没有。

这样一来，弟弟如果努力从 30 分考到 60 分，超出自己预期分数线 20 分，就能得到可观的奖赏。我如果还是 80 多分，增幅不明显，那就算分数比弟弟高，但并不一定多拿太多钱。这样就鼓励了每个人以自己的水平为起点去进步，而不是一味比谁绝对分高。

当然，爸爸也很忙，不是说一旦定了分数线就一劳永逸——他得根据我们的学习状况来不断“自我调节”，因为如果弟弟水平已经到 60 分了，再给他设 40 分的线就不合理了。反之，我要是一直考 85 分没什么波动，也可能需要微调我的分数线。所以，爸爸也需要不断学习，只不过他需要学习的是我和弟弟的学习进度。

数学对应

在 RL 中，我们称这个“分数线”为价值函数 ，它的作用是当参考线（baseline）。于是我们的训练目标从“只用 Reward” 进化成“用 Advantage 来衡量进步”：

对某个状态 下的动作 ，如果实际 Reward 超过了 Critic 的预期，就说明这个动作比期望好；如果低于预期，就说明这个动作没达标。在最简单的情形下，我们的优化目标就变成：

有了这个“分数线”去做差，我们能降低训练过程中的方差；也让高于预期的动作拿到更大的梯度，低于预期的动作被抑制。

加入 Clip 与 min 操作：防止更新过度

有了“分数线”以后，效果确实好了很多。但新的问题出现了：

• 如果某一次考试我突然爆发，进了高分段，比如 95 或 100 分，爸爸会给我极高奖励，导致我在下一次考试前可能“走火入魔”，去尝试各种极端学习方法，成绩忽高忽低，奖励也随之剧烈波动。

为此，爸爸觉得要适度控制我更新学习策略的“步幅”——一次性冲太高也不一定要给我成倍加零花钱。给得太多，会让我产生极端探索心态；给得太少又会抑制热情。总之需要一个平衡。

数学对应

在 PPO（Proximal Policy Optimization）中，这个“平衡”靠“Clip” 操作来完成。我们常见的 PPO 核心目标函数里，有这样一段：

其中

表示新策略与旧策略在这个动作上的概率比值。如果这个比值离 1 太远，就会被 在 区间内，从而限制一次更新幅度别过大。

用故事的话讲，就是：

• 我考到 100 分，可以多拿奖励，但爸爸会有个“封顶”的约束；下一次还要观察一下再做决定，这样保持学习的平稳性，防止出现一条极端的“歪路子”。

Reference Model：防止作弊、极端策略

即便如此，如果我为了追求高分，不惜采取非常规手段——比如考试作弊、威胁老师改卷之类，那不就轻松拿下满分了吗？这显然是违反原则的。而且如果在语言模型场景，可能出现生成有害言论、编造事实等“走歪”的行为。

于是爸爸又提出一个附加约束：

• “无论如何，你不能偏离最初正常学习的方法太多。否则即使你考了高分，我也判你不合格，零花钱也不给。”

这就好比我们在学期开始（也就是监督微调后）的“合规”状态那里画了一条“参照线”，新的行为不能和这个初始策略差太远，否则就要受到惩罚。

数学对应

在 PPO 里，这体现为对 Reference Model（初始策略）的 KL 惩罚，具体可加到 Loss 中，比如：

这样，Actor 不会为了短期 Reward 而脱离原本合理的策略范畴，保证策略在演化过程中不至于“作弊”或偏得太离谱。

GRPO：用“多次模拟成绩平均值”代替价值函数

有一天，爸爸说：“我没空天天衡量你的学习水平了，不想再手动给你画分数线。那你干脆先把试卷做 5 份模拟题，取这 5 次的平均分，这个平均分就是你的预期分数。

真正考试时，如果你比这个平均分高，就说明你表现超出你自己的期望，我就给奖励；不够的话，说明你的表现没到平均线。” 如此一来，弟弟、我，甚至更多同学都可以用“自己多次模拟考试”的均值来做分数线，不需要依赖一个外部（爸爸）不断微调的“价值网络”。

前面几个环节，我们已经看到了 PPO 的思路：Actor + Critic + Clip + KL 惩罚。但在实际应用尤其是大型语言模型（LLM）上，Critic（价值函数）通常需要跟 Actor 同等大小的网络去估计，否则很难评估到位，成本很高，而且有些场景（比如只在回答末尾才有一个整体 Reward）并不太适合训练出精细的价值函数。

这时候就出现了 Group Relative Policy Optimization（GRPO）。它的要点是：

• 不用“学习”一个单独的价值网络当 Critic；
• 而是对同一道题目、同一个状态，先用旧策略采样多条输出，然后把这些输出的平均 Reward 当作 baseline；
• 超过平均值就相当于“正向 Advantage”，低于平均值就是“负向 Advantage”。

在 GRPO 里，除了这一步，还保留了 PPO 中的 Clip 和对 Reference Model 的 KL 正则，这些都可以保障更新的稳定性和合规性。

数学对应

DeepSeekMath 的技术报告里给出了 GRPO 的目标函数（省略部分符号细节）：

其中

就是用同一问题的多条输出做平均，得到一个“相对评分”，再做标准化后作为 Advantage。这便实现了无需单独价值函数也能得到一个动态的“分数线”，让训练更加简单、节约算力。

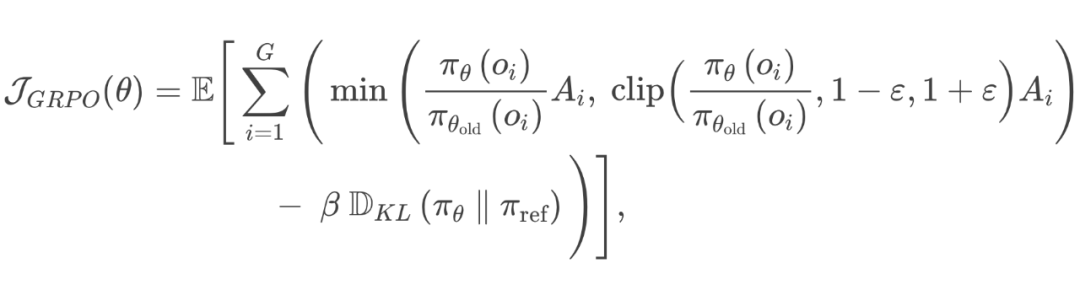
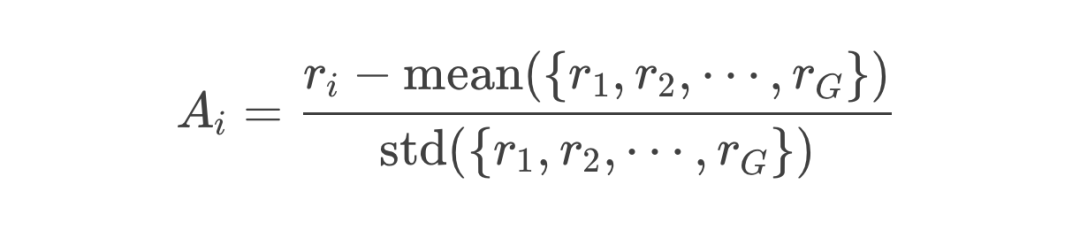
小学每周都考试：多步时序下的新挑战

在前文，我们把一次考试拿到的分数当作 Reward，用 Critic（价值函数）做“分数线”。这解决了“只看绝对成绩”带来的高方差和不公平问题，并且通过 PPO/GRPO 的各种机制（Clip、Reference Model 等）控制策略更新的幅度与合规性。

然而，在真实的学校生活中，考试往往不止一次。想象这样一个情境：

每周一早上，老师都会给我们一张小测验卷子，分值从 0-100 不等；

周一下午爸爸会根据我的测验结果和预期分数线，给我相应的零花钱或惩罚；

周二到周日是我学习、调整策略的时间。比如我要不要去参加补习班？要不要和同学一起自习？还是干脆放飞自我，躺平娱乐？

到了下周一早上，又是一场新测验，继续给分并影响零花钱。如此往复，每周一次考试，一次接着一次地进行。

在这个循环过程中，我的每一次学习计划决策（Action）都会累积影响下一周的测验分数。最终，我希望在这整个学期里总体拿到更多的分数、更多零花钱。这就和前面“只考一次试”有明显的区别了：我们不是只在一场考试后就结束训练，而是持续对每周的表现做评估和更新。

7.1 单步 vs. 多步：新的困惑

• 以前，爸爸只需要在“一次考试”后，评估我的表现是否超出预期，就可以立刻给零花钱，或者在下次测试前稍微修正一下我的分数线（Critic）。
• 现在，每周都有考试，但我下一周的表现，往往也受“这周考完之后做了哪些学习动作”影响。比如这周我选择“熬夜狂刷题”，可能下周突然身体疲惫、精力有限，反而成绩下滑；反之，如果这周我适度学习，下周可能能稳定发挥。

• 更复杂的是，我是不是要做一个长期的规划？可能我前两周稍微放松，第三周再发力冲刺，结果对期末大考更有帮助…… 在强化学习术语里，这已经是一种多步时序决策问题。我们需要照顾到一段时间内的累积表现，而非单一考试。

回到 RL 公式上也类似：如果每周我们都拿到一个奖励 ，并且我们每一周的动作（学习计划）都会影响后续几周的成绩，那么如何去估计某个动作是否好？显然不能只看“本周的考试结果 – 分数线”这么简单，有时需要考虑到后面几周的连锁效应。

7.2 策略 在比喻里的角色

在强化学习的术语中，“策略” 指的是决策规则：给定某个状态 ，我们以多大概率或依据什么方式，去选择一个具体动作 。

• 在小学考试隐喻中，可以想象“策略”就是我的总体学习方法或“选课思路”，它会根据我当前的状态（比如疲惫程度、最近分数波动、是否遇到难点等），来决定本周要不要补习、要不要放空休息、或者做别的准备。

• 动作  就是这周具体采取的学习计划。而策略 则是那个“生成动作”的整体函数或分布。策略越好，就越能在各周做出恰当决策，从而累积更高的长期分数（Reward）。

每次执行了动作 并观测到结果后，我们会更新对策略 的信心，慢慢让它朝着“高分、高 Reward” 方向演化，也就是策略更新的过程。

为了多步时序：TD 残差与 GAE 再登场

随着每周考试的频繁进行，想要在“多次考试累积”下获得高分，就需要更好地“估计本周动作的长期影响”。在强化学习的语言里，这意味着我们不能只在一周的表面 Reward 和预期价值之间做对比，还要兼顾后续周次的回报。

8.1 什么是TD（Temporal Difference）残差？

在强化学习里，我们把每一周看作一个时间步 。我的当前状态（State）可能包括：

• 我当前的学习水平、疲劳程度、对下一次考试范围的掌握度；
• 我上一场考试的得分；

• 甚至我当前的心情（如果要更真实的话……）。

然后，我做出的动作（Action）可以是：“去参加某辅导班”、“自主复习”、“放空休息”等等。当这一周结束时，我会收到一个奖励 （比如下一周的考试成绩或与之相对应的零花钱），并且进入下一周的状态 （新的水平、疲劳度等）。

TD 残差（Temporal Difference Error）就是对“本周价值估计”和“下周实际得到奖励+下周价值估计”之间的差异做一个衡量。形式如下：

这里 是折扣因子，用来表示远期的奖励要衰减一些。

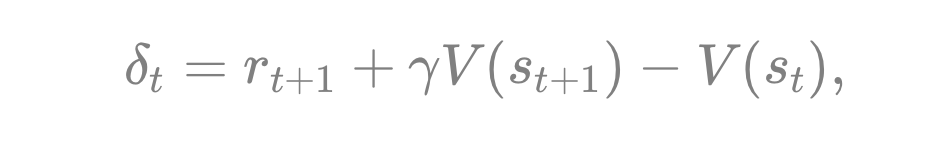
• 小学考试的比喻里，可以理解为：“我原本觉得本周（状态 ）能至少考到 80 分，结果实际只有 75 分，下周又觉得能稳 78 分，所以和最初的期望值一比，发现差了几分。” 它直观反映：“我原先以为本周能拿多少分，加上下周的未来潜力；和实际看到的成绩与未来估计相比，相差多少？”

• 如果 为正，说明“比预期更好”；如果为负，说明“还得多加努力”。

这就是单步的 TD 残差。它能使爸爸（Critic）不断修正对我“当前状态价值” 的估计。

8.2 什么是 GAE？为什么需要它？

问题：如果我们只用单步的 TD 残差，就相当于“每次只看一周后的考试成绩 + 对下一周的估计”，这样做数据更新非常快，方差也可能较小；但有时候会忽略更远期的后果。比如，我本周过度学习，下周的分数也许没崩，但大后周就会累得不行。反之，如果我们用“把所有后续考试的总成绩都算进来”那种蒙特卡洛方法，则要等到很多周过去之后才能总结，这期间的噪声/运气都可能让估计出现超高方差。

GAE（Generalized Advantage Estimation）就像一个“在单步 TD 与全局蒙特卡洛之间”找折衷的办法——用参数 来控制“我们想考察多少步以后的反馈”。它的形式常见于：

其中

就是每个周次上的 TD 残差； 让较远的反馈在估计里比重逐渐减小。

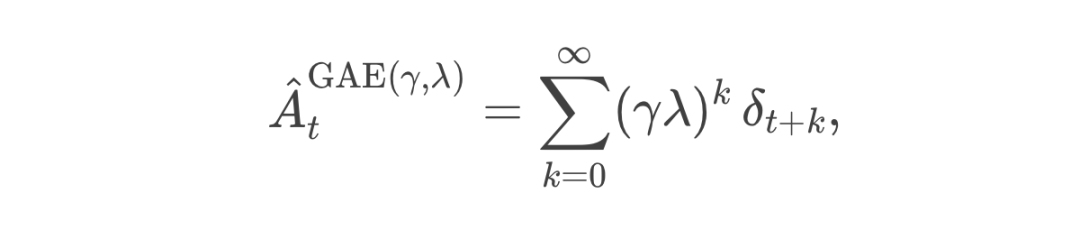
• 当 时，就退化成单步 TD；

• 当 趋向 1 时，就越来越接近全蒙特卡洛估计（当然在实际实现上会有截断）。

比喻拆解

• ：表示“本周 + 下周价值”的偏差；
• ：表示“下周 + 下下周价值”的偏差；
• ……
• 最终，GAE 把这些多周的差值按衰减系数累加起来，就得到一个对“本周这次决策的 Advantage” 更稳定、更综合的评估。

8.3 GAE 在比喻中的具体意义

1. 我（学生）每周都能收到一个基于“上一周考试成绩-预期线”得到的激励，但这个激励也要考虑更远期的趋势——是不是会造成后面几周的成绩起伏？
2. 爸爸想综合地评估：这周的学习动作，对下周及之后几周的影响都可以稍微看一下，但“越远的影响”越需要衰减地去衡量，不至于把噪声无限放大。

3. 这也就解释了为什么只用单步信息会对后几周可能出现的“大跳水”或者“大爆发”视而不见；而全局蒙特卡洛会在多周累积回报上花费太长时间才得到一个结论，还容易出现高方差。

新设定下的价值函数与动作价值函数

跟前面一节的“单次考试”设定相比，现在我们每周一次考试，就自然形成了多步决策。于是我们的状态价值函数和动作价值函数需要重新定义。

1. 状态价值函数

在＂第 周＂时，我的综合水平，疲劳度，最近分数等信息构成了状态 。如果未来所有周都按照当前策略 来学习／休息／补习，那么我能预期拿到多高的累积成绩？

表示：如果从这一周起，按照当前策略 去选择每周的学习动作，一直到学期结束，我能期望拿到多少“累计零花钱”或者“累计加权分数”？

就好像爸爸对“你在本周的整体水平”能在接下来若干周获得多少好成绩的一种预估。

公式：

2. 动作价值函数

如果我在第 周选了 这个具体动作（比如“参加昂贵补习班”），之后各周都继续用 ，我能预期在剩下这些周内获得多少累积成绩？

表示：如果我在周 这样选了动作 ，并且之后所有周都按照策略 来学习，那整个后续我能拿到多少累计分数或收益？

比如说，如果这周我“调整心态，适度复习”，导致分数比较稳，下周也不至于累崩，后面总体回报可能更高。

公式：

3. 优势函数

这代表：你在状态 下选这个动作 ，比起“平均水平”到底好多少？

如果 大于 0，说明这次决策可以在后续几周里带来超过平均的收益；如果小于 0，则说明不如同等水平下的普通复习计划好。

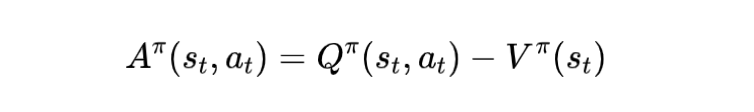
我们到底在用什么 Loss 训练什么？

在 PPO、A3C、GRPO 等常见的策略梯度方法里，背后通常有两部分模型需要训练：

Actor（策略网络）：输出每个状态下我选择各个动作的概率，或直接输出一个最优动作。

Critic（价值网络）：输出状态价值 （或动作价值），作为基准分数线，让我们更稳定地评估动作好坏。

这两者的更新往往通过一个损失函数（Loss）来联合优化。举个典型例子：

• Critic Loss：最常见的是最小均方误差（MSE），让 Critic 的估计 尽量接近我们根据实际反馈（Reward）得到的目标回报。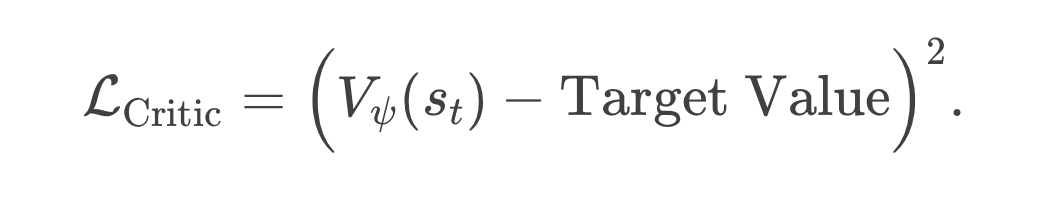
  
  在多周考试里，Target Value 可能是“一步 TD 目标” 或者是更长的回报估计（如 GAE 里累加起来的一部分）。
• Actor Loss：我们会把优势函数  或其某种近似，乘上 来做梯度上升（或等价的负号做下降）。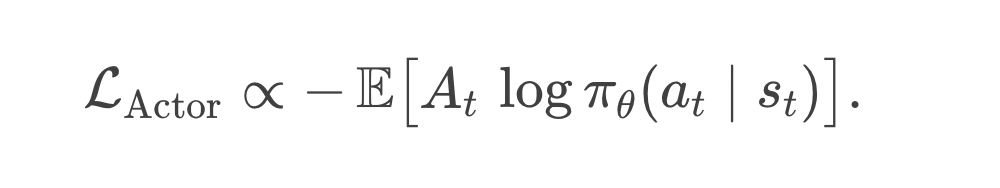
  
  当一个动作在当前状态下的 Advantage 越大（超过分数线越多），就会推动策略朝该动作概率增大的方向更新；反之则相反。

在 PPO/GRPO 里，我们讲过你还会看到 Clip、KL 惩罚等额外项加到 Loss 中，以控制更新幅度别太大、或别偏离初始策略太多。

宏观上来看：

• Actor 就是“我大脑里的决策机制”，不断学着如何选动作。

• Critic 就像“我的内在预期模型”或“家长给的预期分数线”，不断修正对当前学习状态的评估。

• 最终的 Loss 把这两个部分的误差结合在一起，让二者相辅相成地共同进步。

偏差与方差：在“多周考试”的比喻如何体现

在多步时序下，为什么会出现偏差和方差的问题？可以通过几种估计方法对比来看。

1. 全蒙特卡洛：
• 做法：等到好几周的考试都考完、算完所有分数加起来，再回来更新“当初第 周决策的好坏”。
• 好处：长期真实的回报都算进去了，不怎么“偏”。

• 坏处：如果有些考试运气成分高，或者弟弟突然生病，这些偶发因素都会让最终分数波动很大，从而在训练时出现超高的估计方差。

2. 单步 TD：

• 做法：只看“这一周得到的分数 + 对下周的估计”来衡量“本周动作”的好坏。

• 好处：不会因为长远噪声而把评估搞得极不稳定，方差相对较小。

• 坏处：可能忽略后面几周真正的重要影响，估计会产生偏差。

3. GAE：
• 做法：综合若干周（由 参数决定），既能考虑到一些后面几周的效果，又不会把非常远期的噪声全部吸收进来。
• 好处：在“减少偏差”与“压低方差”间折衷，训练更高效、稳定。
• 坏处：需要额外的实现/公式来把多步 TD 残差累加、需要选择合适的 超参数。

用比喻的话讲：

• 偏差意味着：我们判断某周的决策好坏时，可能过于只看眼前（那就会导致长期效果判断出错）。
• 方差意味着：如果我们判断某周决策好坏时，要把今后所有几周都完全算进去，那在这个漫长过程中，“弟弟突然生病”、“试卷难度随机波动”、“我临时遭遇某些突发事件”等都会影响分数，导致我对本周决策的评估极其不稳定。就像猜不准天气一样，太多干扰因素使估计忽上忽下。

GAE 则相当于给“未来几周成绩的影响”打一个权重衰减，每远一步就稍微降低影响力，既不盲目忽略未来，也不会把所有远期噪声一股脑都背上。

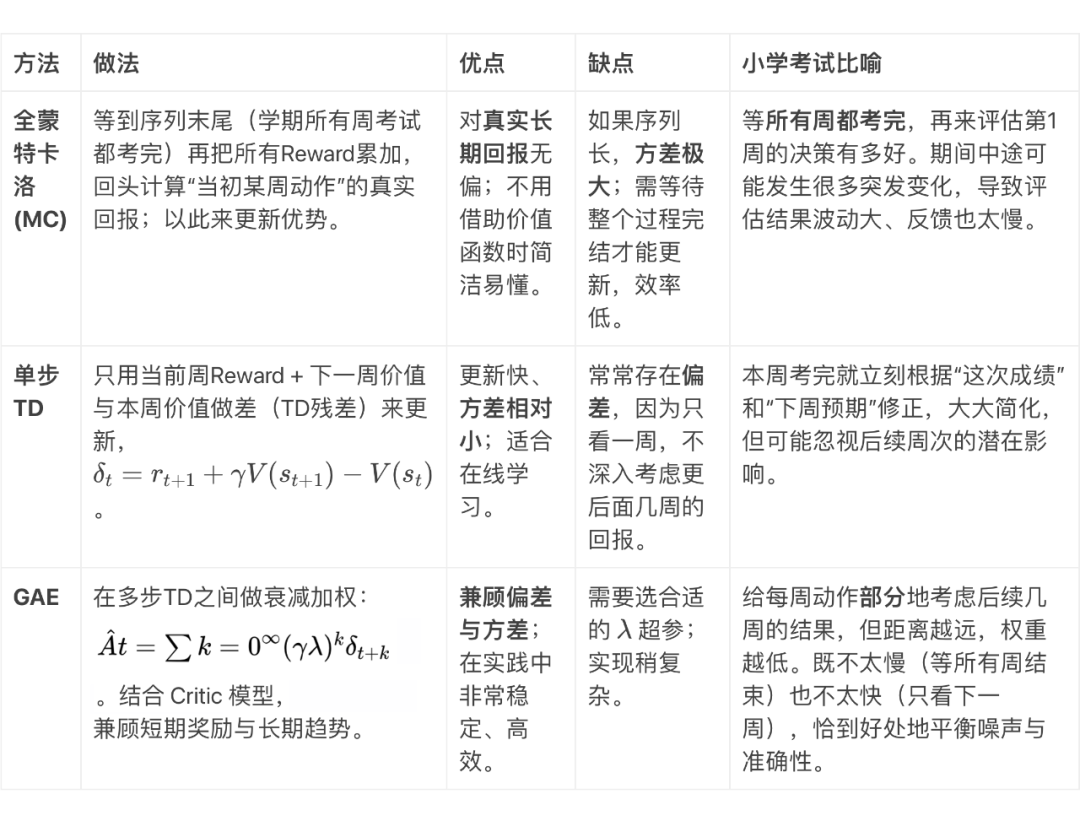
对比三种 Advantage 估计方法

下面给出一个简洁对照表，来梳理全蒙特卡洛、单步 TD、以及 GAE 在多步时序场景下估计优势的差异。虽然你的博客以前没明确提过“全 MC”，但它在 RL 里是一个常见思路，和你“只考一次试”场景更贴近，所以这里做一下简单介绍，以便理解为什么 GAE 是折衷方案。

结语：回顾与展望

通过这个小学考试的比喻，我们逐步从只看绝对分数的朴素思路，演化到 PPO 的完整机制（Critic、Advantage、Clip、Reference Model），再到 GRPO 的创新思路（用一组输出的平均得分当基线，省去价值函数的繁琐）。以下几点值得再次强调：

• Critic 的意义：它为每个状态或阶段提供“合理预期”，大幅降低了训练方差；
• Clip & min 机制：约束策略更新幅度，避免一次考试“爆发”带来的巨幅震荡；
• Reference Model：限制“作弊”或极端行为，让策略不要过度偏离最初合规范围；
• GRPO 的优点：在大型语言模型中，省掉了价值网络，减少内存和计算负担，还与“对比式 Reward Model”天然契合。

就像爸爸改用“让孩子自己多次模拟，然后以平均分当预期线”的思路一样，GRPO 让我们不用再额外维护一个庞大的 Critic，也能获得类似的相对奖励信号。从结果看，这既保持了 PPO 原有的稳定性和合规性，又让训练更直接和高效。

在把“小学考试”扩展到“每周一考”的多步时序情境下，我们发现：

1. 需要用 TD 残差（Temporal Difference）来衡量“实际回报”和“之前对价值的估计”之差；
2. 为了更好地估计 Advantage，既不想只用单步 TD，也不想全靠蒙特卡洛，“GAE（Generalized Advantage Estimation）”应运而生；
3. 它通过对多步 TD 残差进行衰减累加，提供了一个兼顾偏差与方差的折衷方案；
4. 状态价值函数 与动作价值函数 的定义也要放到时序多步的语境下去；在每周进行一次学习决策、每周获得一个奖励，形成了更丰富也更复杂的训练过程。

在实践中，PPO、A3C 等主流策略梯度算法里都经常把 GAE 作为核心组件，用来让 Advantage 的估计更平稳；在大模型微调或语言生成任务里，如果也把每次回答过程拆分成多阶段反馈，就同样可以使用类似 GAE 的思路来平衡“短期 vs. 长期”的奖励评估，得到较好的训练效果。

希望这篇文章能帮助读者更自然地理解 PPO 与 GRPO 的原理，也能在实践中有所启发。如果你对过程监督（Process Supervision）或迭代式强化学习（Iterative RL）等更高级的技巧感兴趣，也欢迎持续关注我的博客。

（文：PaperWeekly）