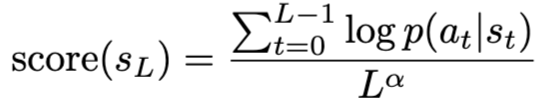AIxiv专栏是机器之心发布学术、技术内容的栏目。过去数年,机器之心AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com
自动形式化数学定理证明,是人工智能在数学推理领域的重要应用方向。此类任务需要将数学命题和证明步骤转化为计算机可验证的代码,这不仅能确保推理过程的绝对严谨性,还能构建可复用的数学知识库,为科学研究提供坚实基础。
早在上世纪中叶,戴维斯、明斯基等不少逻辑学家、数学家、人工智能先驱便已在探索相关问题,其中,也不乏王浩、吴文俊等华人身影。
近些年在 LLM 能力加持下,自动定理证明系统更多依赖于复杂的蒙特卡洛树搜索 (MCTS) 或价值函数 (Value Function) 来指导搜索过程。
然而,这些方法引入了额外计算成本,并增加系统复杂度,使模型在大规模推理任务中的可扩展性受限。
字节跳动豆包大模型团队推出的 BFS-Prover 挑战了这一传统范式。
作为一种更简单、更轻量但极具竞争力的自动定理证明系统,它引入了三项关键技术:1)专家迭代 (Expert Iteration) 与自适应性数据过滤,2)直接偏好优化 (DPO) 结合 Lean4 编译器反馈,3)BFS 中的长度归一化。
从结果看,BFS-Prover 在形式化数学测试集 MiniF2F 上实现了 72.95% 的准确率,创造了新的领域记录。
该结果也首次证明:在合理的优化策略下,简单的 BFS 方法能够超越蒙特卡洛树搜索(MCTS)和价值函数(Value Function)等主流的复杂搜索算法。
目前,论文成果已对外公开,模型也最新开源,期待与相关研究者做更进一步交流。
-
BFS-Prover: Scalable Best-First Tree Search for LLM-based Automatic Theorem Proving
-
https://arxiv.org/abs/2502.03438
-
HuggingFace:https://huggingface.co/bytedance-research/BFS-Prover
Part1:主流方法蒙特卡洛树搜索和价值函数真的必要么?
在形式化数学证明领域,将抽象的数学概念转化为能够用计算机验证的严格形式,是一项极具挑战性的任务。
该过程要求每一步推理都符合严格的形式逻辑规则,且每个步骤都必须经过 Lean 证明助手验证。
在自动形式化定理证明过程中,计算机面临的核心挑战是 —— 在庞大且高度结构化的证明空间中,找出有效路径。这一难点与传统搜索问题有本质区别,具体表现如下:
-
搜索空间庞大:每一步推理可能有数十甚至上百种可能的策略选择;
-
动态变化的策略空间:不同于棋类游戏的固定规则,数学定理证明中,每个状态下可应用的策略集合不断变化,且规模庞大且无明确界限;
-
反馈稀疏与延迟:直到完成证明前,系统很难获得有效的中间反馈;
-
开放式推理过程:缺乏明确的终止条件,证明尝试可能无限延续;
现有自动定理证明系统如 DeepSeek-Prover-V1.5、InternLM2.5-StepProver 和 HunyuanProver,主要依赖复杂的蒙特卡洛树搜索(MCTS)和价值函数(Value Function)解决上述问题。
这些类 AlphaZero 算法框架在游戏中表现出色,尤其在围棋领域大放异彩,推动了强化学习概念破圈。但在自动定理证明领域,由于状态空间极其复杂以及缺乏明确的过程奖励信号,上述主流方法效果并不理想。此外,复杂的搜索算法还带来了计算成本高、系统复杂度增加等问题。
Part2:化繁为简,用机器证明数学定理可以更简单
人类遇到问题,往往优先采用最可能解决的方法。最优先树搜索(Best-First Tree Search,即 BFS)与之类似。
这是一种在 “树” 或 “图” 中搜索节点的算法。核心思想是根据某种启发式函数,评估每个节点优先级,按优先级访问节点,常用于解决约束满足问题和组合优化问题,特别是在需要快速找到近似最优解的情况下。
此前不少研究者认为,简单的 BFS 算法缺乏有效的探索机制,尤其是对深度路径的探索,难以胜任大规模定理证明任务,但豆包大模型团队的研究者发现了其中的突破口,并提出了 BFS-Prover 系统。
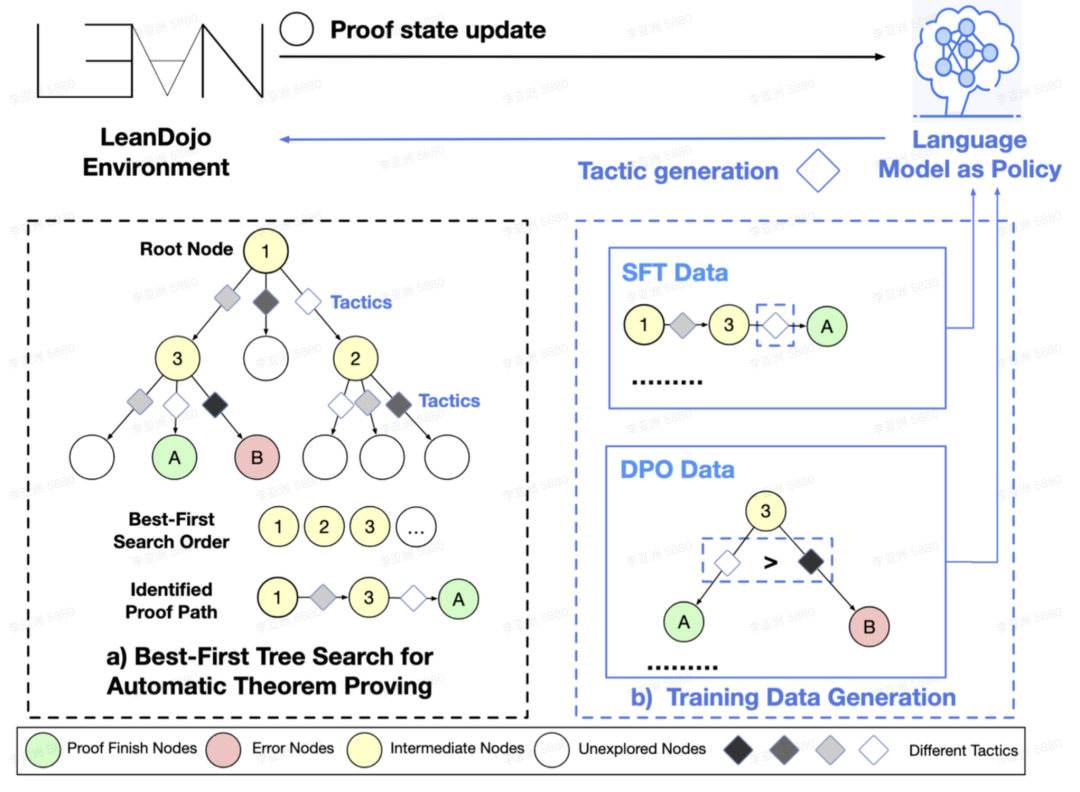
下图展示了 BFS-Prover 系统的整体架构和工作流程。
右侧展示了训练数据生成过程,包括用于监督微调的 SFT 数据 (成功证明路径上的状态 – 策略对) 和用于直接偏好优化的 DPO 数据 (从同一状态出发的正确策略与错误策略的对比)。
左侧展示了 BFS 机制,通过 LeanDojo 环境与 Lean4 交互,从根节点开始,按照优先级顺序 (1→2→3…) 探索证明路径,直到找到证明完成节点 (绿色 A 点)。
整个系统形成闭环:LLM 生成策略 → LeanDojo 执行 → 获取反馈 → 生成训练数据→优化 LLM → 再次生成策略,实现了持续改进的专家迭代机制。
团队认为,BFS-Prover 系统不仅证明了经过优化的 BFS 方法性能方面可以超越复杂的 MCTS 和价值函数,并且能保持架构的简洁性和计算效率。其技术特征如下:
BFS-Prover 采用专家迭代框架,通过多轮迭代不断增强 LLM 能力。在每轮迭代中,系统会先使用确定性的束搜索 (Beam Search) 方法过滤掉容易解决的定理,将这些 “简单问题” 从训练数据中剔除,再着手解决 “复杂问题”。
这一数据过滤机制颇具创新性,确保了训练数据逐渐向更具挑战性的定理证明任务倾斜,使 LLM 能够学习更多元化的证明策略。
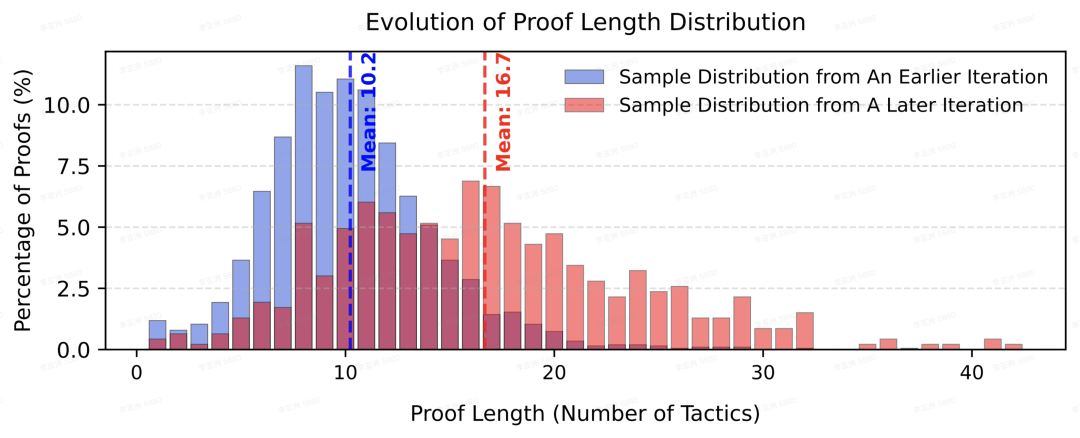
如下图实验数据显示,随迭代进行,系统能够发现证明的平均长度变长,覆盖面变广,证明了这一方法的有效性。
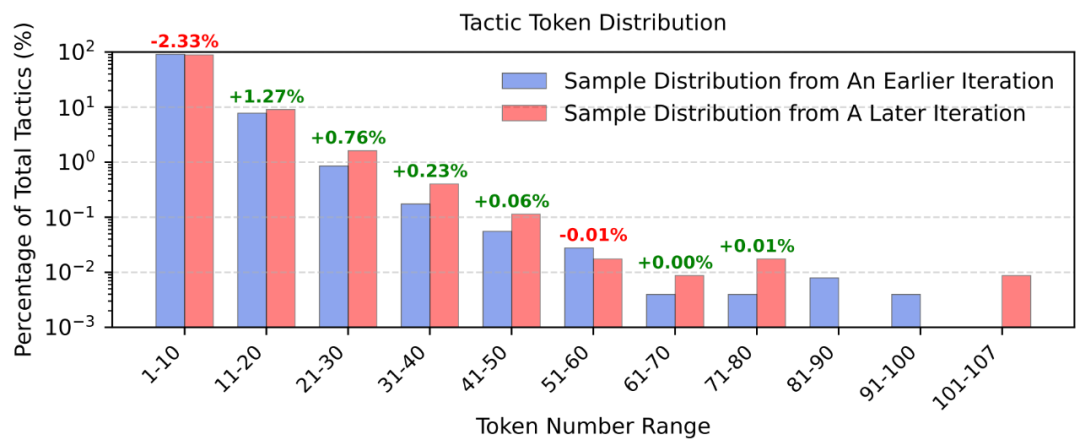
如下图所示,经过多轮迭代,模型生成的策略长度分布发生了显著变化:非常短的策略(1-10 个 token)比例下降,而中等长度策略(11-50 个 token)比例则有所增加。
这种分布变化表明,LLM “深度思考能力” 在加强,避免了常见的强化学习导致的分布坍缩问题,并逐渐掌握了更复杂、更信息丰富的证明策略。
同时,模型生成简洁策略的能力并未摒弃。这种多样策略生成能力的保持对于有效定理证明至关重要,因为不同的证明状态,需要不同复杂度的策略,涵盖从简单的项重写到复杂的代数操作。
在证明搜索过程中,当 LLM 生成的某些策略导致 Lean4 编译器错误,系统将这些无效策略与成功策略配对,形成负反馈信号。
BFS-Prover 创新性地依靠这些数据,基于直接偏好优化 (DPO) 技术优化策略 LLM。此种方法显著提高了模型识别有效策略的能力,优化了策略分布,提高 BFS 的采样效率。
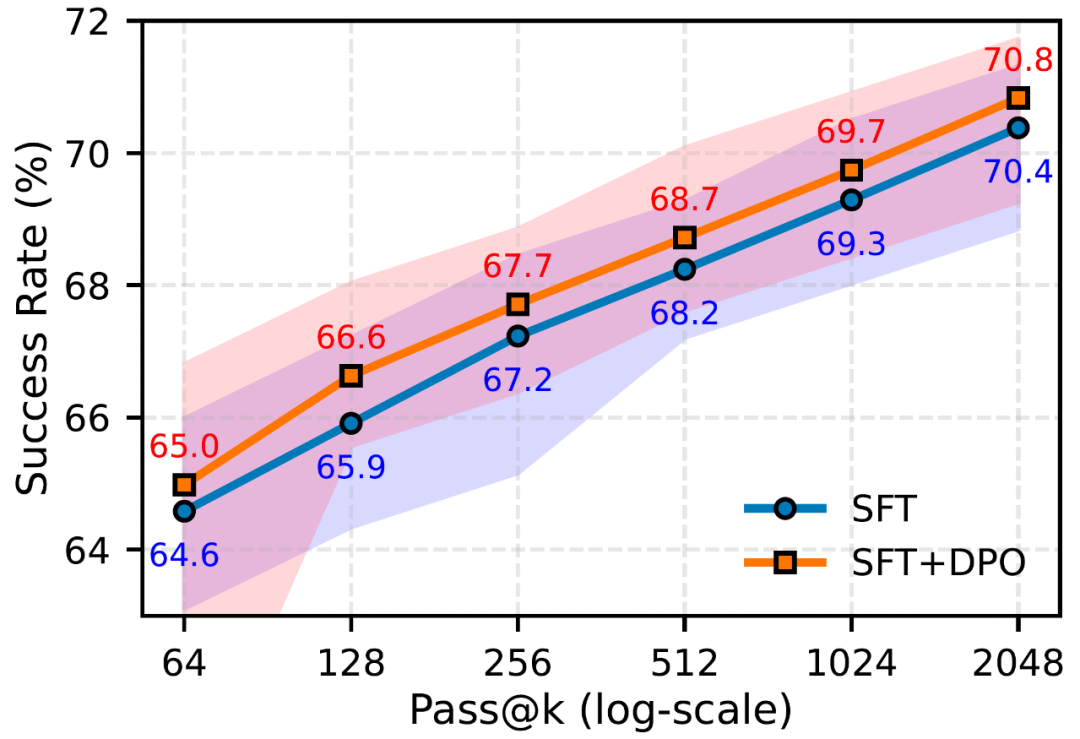
如下图实验结果,在各种计算量级下,经过 DPO 优化的模型均取得了性能提升,证明了负面信号在定理证明中的重要价值。
为解决 BFS 对深度推理路径的天然打压问题,BFS-Prover 系统引入了可调节的长度归一化评分函数:
其中,L 表示路径长度,α 是可调节的长度归一化参数。通过适当调整 α 值,系统可以平衡对高概率路径的利用与对深层路径的探索,使 BFS 能够更有效地探索长链证明。
Part3:BFS-Prover 取得 MiniF2F 新 SOTA
团队在 MiniF2F 测试集上,对 BFS-Prover 进行了全面评估。该测试集是形式化数学领域公认的基准测试集,包含高难度的竞赛级数学问题,被广泛用于衡量自动定理证明系统的能力。
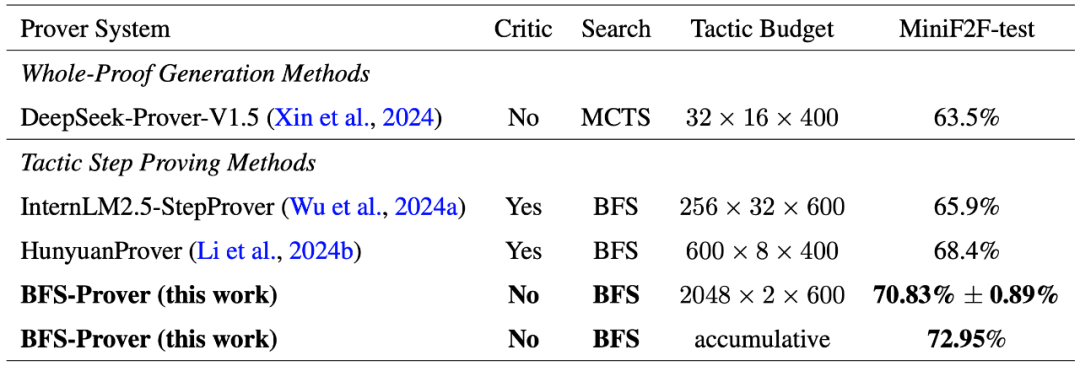
在与领先的定理证明系统的对比中,BFS-Prover 展现出显著优势。
在固定策略生成的计算量下 (2048×2×600 次推理调用),BFS-Prover 实现了 70.83% 的准确率,超过所有现有系统,包括使用价值函数的 InternLM2.5-StepProver (65.9%) 、HunyuanProver (68.4%),以及基于 MCTS 的 DeepSeek-Prover-V1.5 (63.5%)。
在累积评估中,BFS-Prover 进一步将准确率提升至 72.95%,成为了形式化定理证明领域的 SOTA。
这一结果不仅证明了 BFS 方法的潜力,更展示了通过精心设计可以使简单算法超越复杂方法。
值得一提的是,BFS-Prover 成功证明了 MiniF2F-test 中的多个 IMO 问题,包括 imo_1959_p1,imo_1960_p2, imo_1962_p2, imo_1964_p2 和 imo_1983_p6。
这些证明展示了系统在处理复杂数学推理方面的强大能力,涵盖数论、不等式和几何关系等。
比如,对于 imo_1983_p6 不等式问题,BFS-Prover 能够生成简洁而优雅的形式化证明:
团队认为,BFS-Prover 的成功,暗含了自动定理证明领域的一项重要启示:简洁的算法结合精心设计的优化策略,同样有助于 AI4Math 边界拓展。
随着大语言模型能力的不断提升,BFS-Prover 开创的简洁高效路线有望进一步推动自动形式化定理证明领域发展,为数学研究提供更强大的自动化工具支持。
展望未来,团队计划进一步提升 BFS 方法在处理更复杂数学问题上的能力,特别是针对本科和研究生级别的数学定理。同时,团队也将基于推理模型和其他前沿路线,持续挖掘模型潜力。
团队期望,通过持续优化数据和训练策略,让相关工具为数学研究提供强大辅助,加速数学发现过程,最终实现人机协作解决前沿数学挑战的愿景。
(文:机器之心)