【CUDA编程】关于矩阵乘加操作的四个指令(ldmatrix、mma、stmatrix、movmatrix)详解
写在前面:在 GPU Tensor Core 的编程实践中,笔者此前通过矩阵乘法优化的案例分析,已初步探讨过基于 CUDA 官方 WMMA API 的基础实践。这类高层抽象接口虽能快速实现加速,但若要释放 Tensor Core 的极致性能,则需深入硬件指令层级展开优化。CUTLASS 库的 cute 组件正展现了这一设计理念——其矩阵拷贝(copy)和矩阵乘加(mma)等核心操作均直接基于 PTX 汇编指令构建,通过底层指令级的灵活编排实现更高性能。本文将聚焦矩阵乘加运算的四个核心指令(ldmatrix、mma、stmatrix、movmatrix),解析其运作机制与优化策略,同时结合 cute 库的封装实现进行对照阐释。
1 矩阵乘加操作
废话少说,矩阵乘加操作是指具有如下形式的计算任务:
其中 是四个矩阵,和被称为累加矩阵,并且和有可能是同一个矩阵。针对这类矩阵乘加操作,PTX 提供了两种计算指令:wmma 指令和 mma 指令。除了 PTX 指令以外,在mma.h头文件的nvcuda 命名空间中还提供了一套 WMMA API,不过我们本文的重点在于 PTX mma 指令,对于这两块内容不做介绍。
类似于 wmma 指令, mma 指令也需要所有线程在 warp 中集体执行计算,但是在调用 mma 操作之前,需要在 warp 的不同线程之间显式分配矩阵元素。也就是说,从 CUDA 编程的角度来说,mma 指令是一个 warp 级的集体操作,不允许有分支发散,否则可能造成未定义的行为,同时在使用 mma 指令之前,开发人员必须要清楚每个线程的寄存器中具体存的是几个矩阵的哪几个位置的元素。
mma 指令仅支持有限形状、有限数据类型的 矩阵,具体可以参考 PTX 文档,这里不再详细列出。在矩阵乘加操作中我们通常用(有时也用小写)三个数字来表示矩阵形状,即是一个矩阵,B 是一个矩阵,而和是矩阵。本文中我们以m16n8k16且数据类型f16f16f16f16 为例对 mma 这套指令进行研究,主要有数据加载指令 ldmatrix、矩阵乘加指令 mma 以及数据存储指令 stmatrix,这几个指令本质上都是为 mma 服务的,所以简单起见,先从 mma 指令开始介绍。
2 mma 指令
以形状为 m16n8k16 的半精度矩阵乘法为例,mma 指令语法如下:
mma.sync.aligned.m16n8k16.row.col.dtype.f16.f16.ctype d, a, b, c;先来逐步看一下指令的限定符和参数:
-
• mma表示这个指令执行的是一个矩阵乘加操作。 -
• .sync表示这个指令自带一个屏障的效果,范围是 warp,即执行线程会等待 warp 内所有的线程执行指令结束再往下执行。 -
• .aligned表示 warp 中的所有线程必须执行相同的 mma 指令。不允许 warp 内分支发散,否则行为是未定义的。 -
• .m16n8k16表示参与矩阵的形状,即A矩阵的形状为[16, 16],B矩阵的形状为[16, 8],C矩阵的形状为[16, 8]。 -
• .row和.col表示A和B矩阵的内存排序,即A矩阵是行主序,B矩阵是列主序。要注意的是,在mma.sync.aligned.m16n8k16场景下仅支持.row.col这种入参。 -
• .dtype是矩阵D的数据类型,支持.f64、.f32、.f16三种。 -
• .f16.f16表示A矩阵和B矩阵的数据类型均为f16。 -
• .ctype是矩阵C的数据类型,支持.f64、.f32、.f16三种。 -
• d, a, b, c分别指的是 4 个参与矩阵的寄存器,即输入输出参数。
前面介绍过,mma 指令的是一个 warp 级的集体操作,通过一个 warp 内的所有线程共同完成形状为 m16n8k16 的半精度矩阵乘法,矩阵的元素存储在每个线程的寄存器中。也就是说,要完成指定的矩阵乘法,就要在执行 mma 指令前将矩阵拆分,将矩阵中的元素分配给 warp 内每一个线程的特定寄存器。下面我们来分别看一下 warp 内的线程持有的矩阵元素。
2.1 矩阵 A 的布局
由于是矩阵元素的类型是 f16,占 2 个字节,而线程内每个寄存器占有 4 个字节,所以每个寄存器会包含 2 个 f16 元素。矩阵 A 的形状为 [16, 16] 共 256 个元素,而 warp 内共有 32 个线程,所以每个线程将持有矩阵 A 的 8 个元素,占用 4 个寄存器,不同线程持有的矩阵元素布局如下:

从图上看,一个 [16, 16] 矩阵被分为 4 个 [8, 8] 子矩阵,A 矩阵中子矩阵的排布是列主序的,子矩阵内部是行主序的。具体来说我们以下面这个元素值与索引值对应的 [16, 16] 矩阵为例。
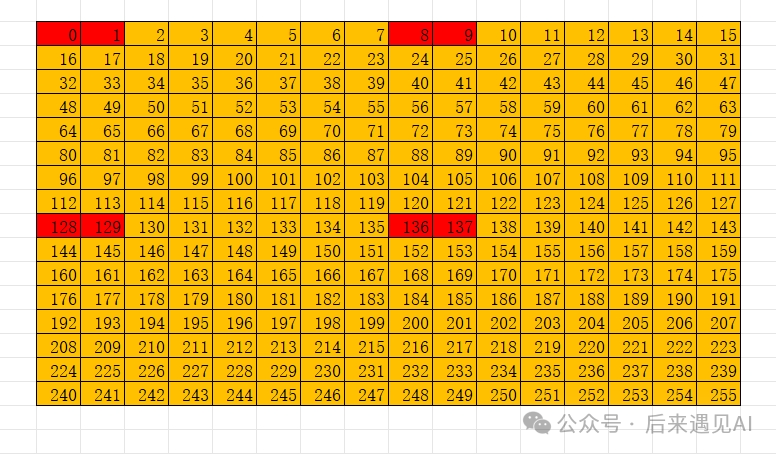
线程 0 的 4 个寄存器中分别存储矩阵 A 的 0 1、128 129、8 9、136 137 共 8 个元素,同理线程 1 的 4 个寄存器分别存储 2 3、130 131、10 11、138 139 共 8 个元素,以此类推。
换个角度,如果我们希望参与 mma 指令计算的 A 矩阵长上面这个样子,我们要提前想办法将每个线程的 4 个寄存器中的元素按上图填充,填充的方式有多种,正好 mma 这套指令对应的有一个 ldmatrix 指令专门用来做这个事,这个后面再讲。
2.2 矩阵 B 的布局
矩阵 B 的形状为 [16, 8] 共 128 个元素,而 warp 内共有 32 个线程,所以每个线程将持有矩阵 B 的 4 个元素,占用 2 个寄存器,不同线程持有的矩阵元素布局如下:
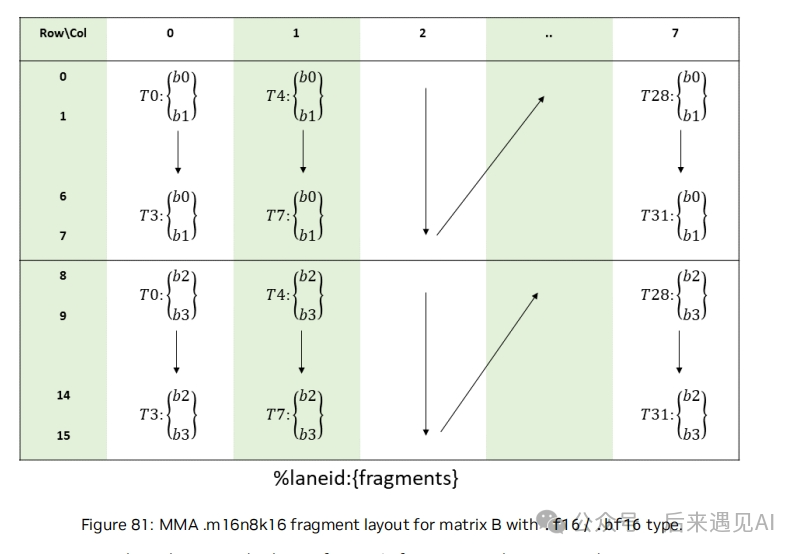
从图上看,一个 [16, 8] 矩阵被分为 2 个 [8, 8] 子矩阵,B 矩阵中子矩阵的排布是列主序的,子矩阵内部是列主序的,这点跟 A 矩阵有所不同,这是因为 mma.sync.aligned.m16n8k16.row.col 指令中指定了 B 矩阵必须是列主序。具体来说我们以下面这个元素值与索引值对应的 [16, 8] 矩阵为例。
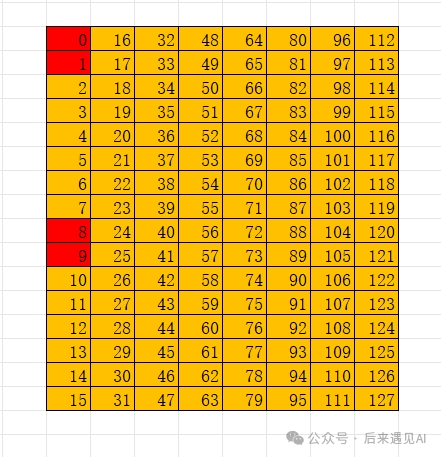
线程 0 的 2 个寄存器中分别存储矩阵 B 的 0 1、8 9 共 4 个元素,同理线程 1 的 4 个寄存器分别存储 2 3、10 11 共 4 个元素,以此类推。
换个角度,如果我们希望参与 mma 指令计算的 B 矩阵长上面这个样子,我们要提前想办法将每个线程的 2个寄存器中的元素按上图填充。
2.3 矩阵 C 和 D 的布局
矩阵 C 和 D 的形状为 [16, 8] 共 128 个元素,而 warp 内共有 32 个线程,所以每个线程将持有矩阵 C 和 D 的 4 个元素,占用 2 个寄存器,不同线程持有的矩阵元素布局如下:
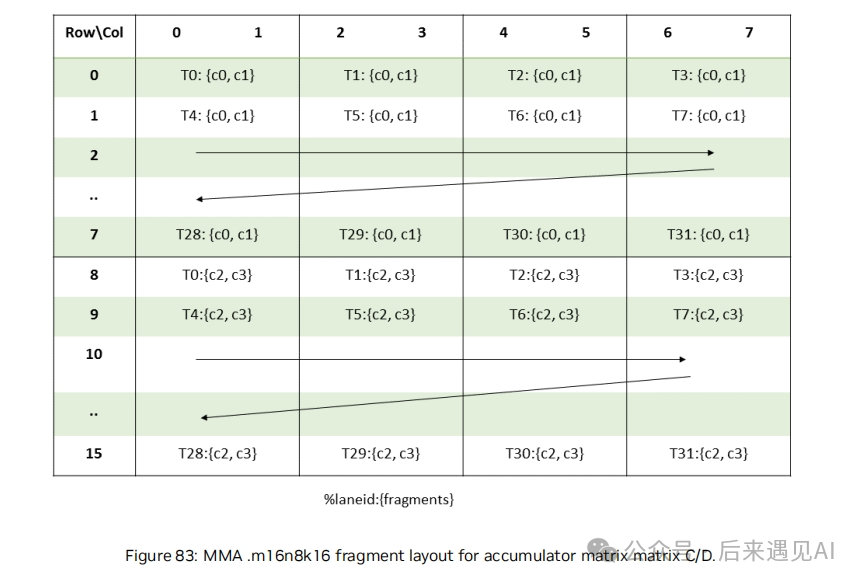
从图上看,一个 [16, 8] 矩阵被分为 2 个 [8, 8] 子矩阵, C 和 D 矩阵中子矩阵的排布是列主序的,子矩阵内部是行主序的。
2.4 对应于 cute 库中的 mma 抽象概念
对应于上述 mma 指令,cute 库也有相应的 mma 抽象概念,通常被封装为 mma Operation,以本文讨论的 mma 指令 mma.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16 为例,其对应于结构体 SM80_16x8x16_F16F16F16F16_TN,我们不妨来看一下源码:
struct SM80_16x8x16_F16F16F16F16_TN
{
...
CUTE_HOST_DEVICE static void
fma(uint32_t & d0, uint32_t & d1,
uint32_t const& a0, uint32_t const& a1, uint32_t const& a2, uint32_t const& a3,
uint32_t const& b0, uint32_t const& b1,
uint32_t const& c0, uint32_t const& c1)
{
#if defined(CUTE_ARCH_MMA_SM80_ENABLED)
asm volatile(
"mma.sync.aligned.m16n8k16.row.col.f16.f16.f16.f16 "
"{%0, %1},"
"{%2, %3, %4, %5},"
"{%6, %7},"
"{%8, %9};\n"
: "=r"(d0), "=r"(d1)
: "r"(a0), "r"(a1), "r"(a2), "r"(a3),
"r"(b0), "r"(b1),
"r"(c0), "r"(c1));
#else
CUTE_INVALID_CONTROL_PATH("Attempting to use SM80_16x8x16_F16F16F16F16_TN without CUTE_ARCH_MMA_SM80_ENABLED");
#endif
}
};从源码可以看出,其 fma 方法直接就是封装了一个 mma 的 ptx 指令,同时我们也不妨 print 一下 cute 里面的 mma atom 对象进行比对,代码如下:
TiledMMA mmaC = make_tiled_mma(MMA_Atom<SM80_16x8x16_F16F16F16F16_TN>{},
Layout<Shape<_1, _1>>{});
print_latex(mmaC);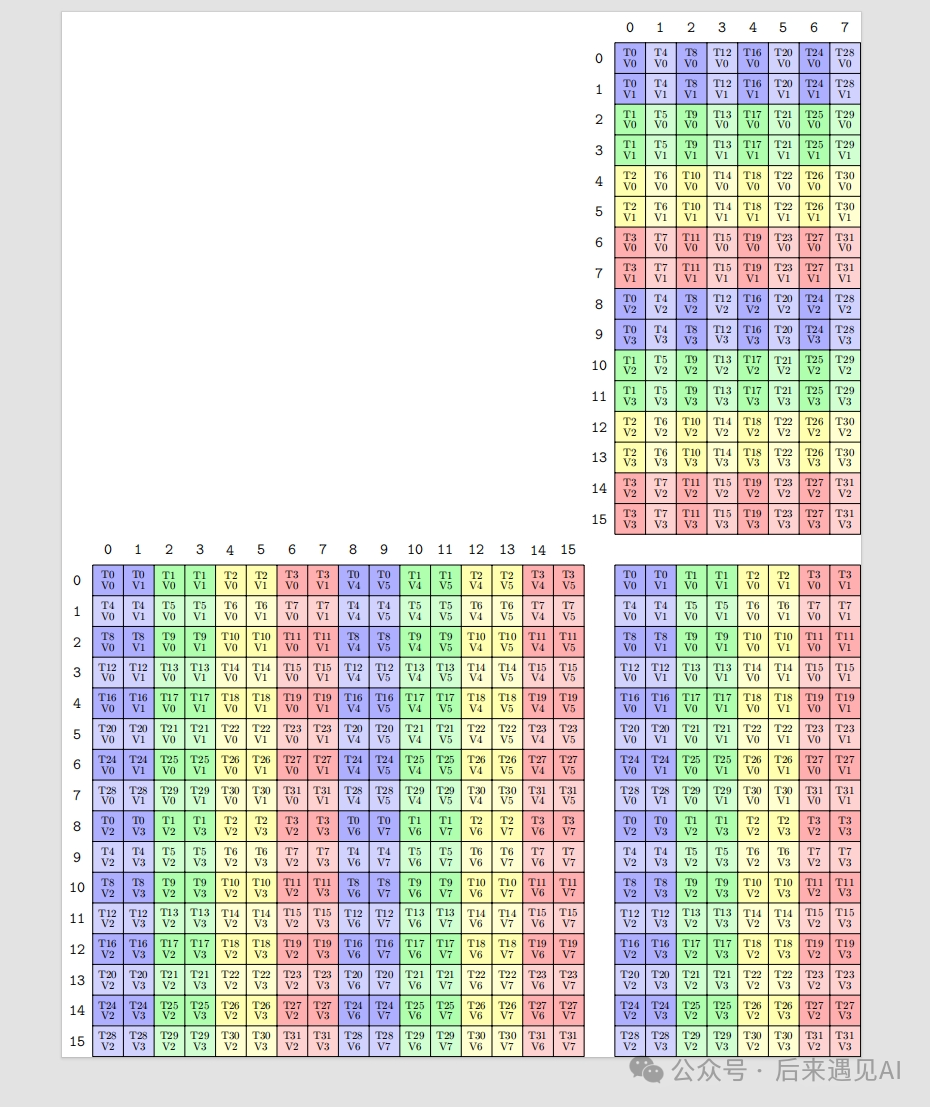
从生成的 mmaC layout 可以看出线程持有几个参与矩阵的元素布局与前面介绍的完全一致。
3 ldmatrix 指令
从前面 mma 指令指定的线程持有的矩阵元素排布可以看出,每个线程持有的元素在原矩阵中并不连续,比如对于矩阵 A 而言,线程 0 持有 0 1、128 129、8 9、136 137 共 8 个元素,因此如果手动填充寄存器,则需要大量的索引计算,因此 PTX 提供了 ldmatrix 指令用来加载数据并分配到每个线程的寄存器中,该指令从 shared memory 中加载一个或多个矩阵到寄存器,通常与 mma 指令配套使用。
熟悉 WMMA API 的读者都知道,在 WMMA API 中也有一个加载函数,即 wmma::load_matrix_sync,可以一次性将一整个矩阵加载到寄存器中,这是官方提供的一个高度封装的 API,使用起来非常方便,但灵活性不足,通常会产生 shared memory 的 bank conflict。与之对应的 ldmatrix 指令则更加底层且灵活,可以结合 swizzle 机制避免 bank conflict,ldmatrix 指令语法如下:
ldmatrix.sync.aligned.shape.num{.trans}{.ss}.type r, [p];
ldmatrix.sync.aligned.m8n16.num{.ss}.dst_fmt.src_fmt r, [p];
ldmatrix.sync.aligned.m16n16.num.trans{.ss}.dst_fmt.src_fmt r, [p];
.shape = {.m8n8, .m16n16};
.num = {.x1, .x2, .x4};
.ss = {.shared{::cta}};
.type = {.b16, .b8};
.dst_fmt = { .b8x16 };
.src_fmt = { .b6x16_p32, .b4x16_p64 };ldmatrix 指令的限定符和参数解释如下:
-
• ldmatrix.sync.aligned表示这是一个加载矩阵的指令,自带一个屏障的效果,范围是 warp,即执行线程会等待 warp 内所有的线程执行指令结束再往下执行。warp 中的所有线程必须执行相同的 ldmatrix 指令,不允许 warp 内分支发散,否则行为是未定义的。 -
• .shape限定符指定了正在加载的矩阵的维度,m8n8表示一次加载一个[8, 8]矩阵。 -
• .num表示总共需要加载多少个形状为.shape的矩阵,以m8n8为例,则.x1表示加载矩阵维度为[8, 8],.x2表示最终加载矩阵的维度为[16, 8],.x4表示最终加载矩阵的维度为[16, 16]。 -
• .trans是一个可选参数,表示是否需要将矩阵转置。 -
• .shared{::cta}是针对线程块集群和分布式共享内存的场景,本文不做讨论。 -
• .type指定了矩阵的数据类型。.dst_fmt和.src_fmt分别指定了目标矩阵和源矩阵的元素类型。 -
• r是目标寄存器。 -
• p是 shared memory 空间中的地址,如果没有指定.shared{::cta}则使用通用寻址。
由于本文讨论的是一个形状为 m16n8k16 的半精度矩阵乘法,所以对矩阵 A 应使用 ldmatrix.sync.aligned.m8n8.x4 指令,而对矩阵 B 应使用 ldmatrix.sync.aligned.m8n8.x2 指令,.type 均为 b16,下面我们来解释一下 ldmatrix 的执行逻辑。
首先 ldmatrix 是一个 warp 级别的数据加载指令,并且是按行进行加载,比如以 m8n8.x1为例(即一个[8, 8]矩阵),被分为 8 行加载,这 8 个行可以不连续,也就是说这个[8, 8]矩阵的主维度可以不是 8(比如是从一个[16, 16]矩阵中截取的一个子矩阵),那么就产生了 8 个共享内存空间的地址对应每行的首地址,这 8 个源地址需要依次赋给线程 0-7 的源地址p参数。注意,这并不意味着 warp 内的其他 16 个线程可以不执行这个指令,其他线程一样执行指令并给 p 赋值,只是赋的值不会被使用而已。而对于m8n8.x2和m8n8.x4的场景,每行的首地址需要分别赋给线程 0-15 和线程 0-31 的源地址p 参数,如下图所示:

还是以 m8n8.x1 为例,虽然只有前 8 个线程中的源地址 p 参数被赋了有效值,但其他线程也会参与此次矩阵加载,一行 8 个 half 元素被连续的 4 个线程加载,每个线程加载 2 个元素,对应一个寄存器。也就是说,首地址赋给线程 0 的这一行元素,被加载到了线程 0-3 的寄存器中,首地址赋给线程 1 的一行元素,被加载到了线程 4-7 的寄存器中,依次类推。
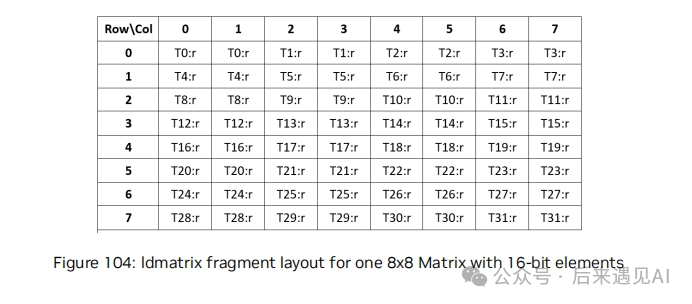
而对于 m8n8.x2 和 m8n8.x4 场景,不过就是重复加载几次 m8n8 矩阵,并将元素依次加载到 warp 内线程的后续寄存器罢了。
3.1 加载矩阵 A
不难发现,上面的线程寄存器中持有的元素在原矩阵中的位置正好与 mma 指令的矩阵 A (非转置)对应起来。讲到这里,对于矩阵 A[16, 16] 的加载方式,我们可以通过如下代码实现,假设矩阵 A 是行主序排布:
#define LDMATRIX_X4(R0, R1, R2, R3, addr) asm volatile("ldmatrix.sync.aligned.x4.m8n8.shared.b16 {%0, %1, %2, %3}, [%4];\n" : "=r"(R0), "=r"(R1), "=r"(R2), "=r"(R3) : "l"(__cvta_generic_to_shared(addr)))
LDMATRIX_X4(RA[0], RA[1], RA[2], RA[3], s_a + (lane_id % 16) * 16 + (lane_id / 16) * 8);在计算地址的时候,要注意一点,A 矩阵中子矩阵的排布是列主序的,这也是为了迎合 mma 指令对矩阵 A 的要求。
3.2 加载矩阵 B
在加载矩阵 B 的时候与矩阵 A 有所不同,首先是矩阵 B 的形状为 [16, 8],所以应该使用 m8n8.x2 指令,其次 mma 指令要求矩阵 B 是列主序的,此时就需要考虑矩阵 B 的原始内存排序,即在 shared memory 中的内存布局,我们分别来讨论一下行主序和列主序这两种情况。
首先来说一下列主序的情况,即矩阵 B 的内存布局为 (16, 8):(1, 16)(这是 cute 中的写法),此时矩阵 B 的元素和索引(索引值也是元素值)如图所示,加载时在 ldmatrix 指令中也无需转置,代码如下:

#define LDMATRIX_X2(R0, R1, addr) asm volatile("ldmatrix.sync.aligned.x2.m8n8.shared.b16 {%0, %1}, [%2];\n" : "=r"(R0), "=r"(R1) : "l"(__cvta_generic_to_shared(addr)))
LDMATRIX_X2(RB[0], RB[1], s_b + (lane_id % 8) * 16 + ((lane_id / 8) % 2) * 8);将上半部分矩阵的每个列的首地址赋给前 8 个线程的源地址 p 参数,下半部分矩阵的每个列的首地址赋给线程 8-15 的源地址 p 参数。
再来说一下矩阵 B 为行主序的情况,即矩阵 B 内存布局为 (16, 8):(8, 1),此时矩阵 B 的元素索引如图所示:
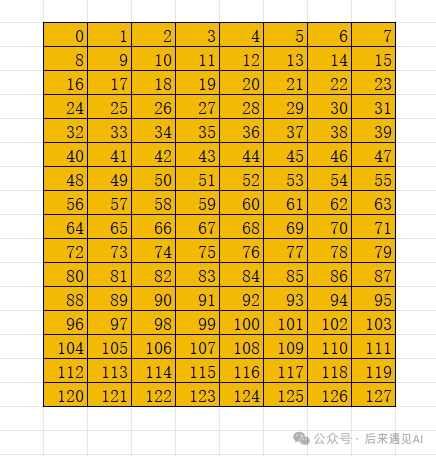
可以发现,此时元素值与索引值不再对应,如果还采用上述的代码加载,那么线程 0 将持有 0 16 8 24 共 4 个元素,这显然与我们的期望是不符的,所以需要用到 ldmatrix 的转置参数 .trans,代码如下:
#define LDMATRIX_X2_T(R0, R1, addr) asm volatile("ldmatrix.sync.aligned.x2.trans.m8n8.shared.b16 {%0, %1}, [%2];\n" : "=r"(R0), "=r"(R1) : "l"(__cvta_generic_to_shared(addr)))
LDMATRIX_X2_T(RB[0], RB[1], s_b + (lane_id % 16) * 16);从代码中可以看出,源地址的传参参考矩阵 A 用行主序的方式计算索引即可,加载的时候指令会根据 .trans 参数自行完成 warp 内线程寄存器数据的交换,交换完成后矩阵 B 就持有 0 1、8 9 共 4 个元素,这正是我们所期望的。
3.3 对应于 cute 库中的 copy 抽象
同样地,cute 库也有相应的 copy抽象概念,通常被封装为 copy Operation,以本文讨论的 ldmatrix 指令 ldmatrix.sync.aligned.x4.m8n8.shared.b16 为例,其对应于结构体 SM75_U32x4_LDSM_N,我们不妨来看一下源码:
struct SM75_U32x4_LDSM_N
{
...
CUTE_HOST_DEVICE static void
copy(uint128_t const& smem_src,
uint32_t& dst0, uint32_t& dst1, uint32_t& dst2, uint32_t& dst3)
{
#if defined(CUTE_ARCH_LDSM_SM75_ACTIVATED)
uint32_t smem_int_ptr = cast_smem_ptr_to_uint(&smem_src);
asm volatile ("ldmatrix.sync.aligned.x4.m8n8.shared.b16 {%0, %1, %2, %3}, [%4];\n"
: "=r"(dst0), "=r"(dst1), "=r"(dst2), "=r"(dst3)
: "r"(smem_int_ptr));
#else
CUTE_INVALID_CONTROL_PATH("Trying to use ldmatrix without CUTE_ARCH_LDSM_SM75_ACTIVATED.");
#endif
}
};从源码可以看出,其 copy 方法直接就是封装了一个 ldmatrix 的 ptx 指令,同时我们也不妨 print 一下 cute 里面的 copy atom 对象进行比对,代码如下:
void ldmatrixLayout() {
TiledMMA mmaC = make_tiled_mma(MMA_Atom<SM80_16x8x16_F16F16F16F16_TN>{},
Layout<Shape<_1, _1>>{});
Copy_Atom<SM75_U32x4_LDSM_N, cute::half_t> s2r_atom_A;
TiledCopy s2r_copy_a = make_tiled_copy_A(s2r_atom_A, mmaC);
print_latex(s2r_copy_a);
}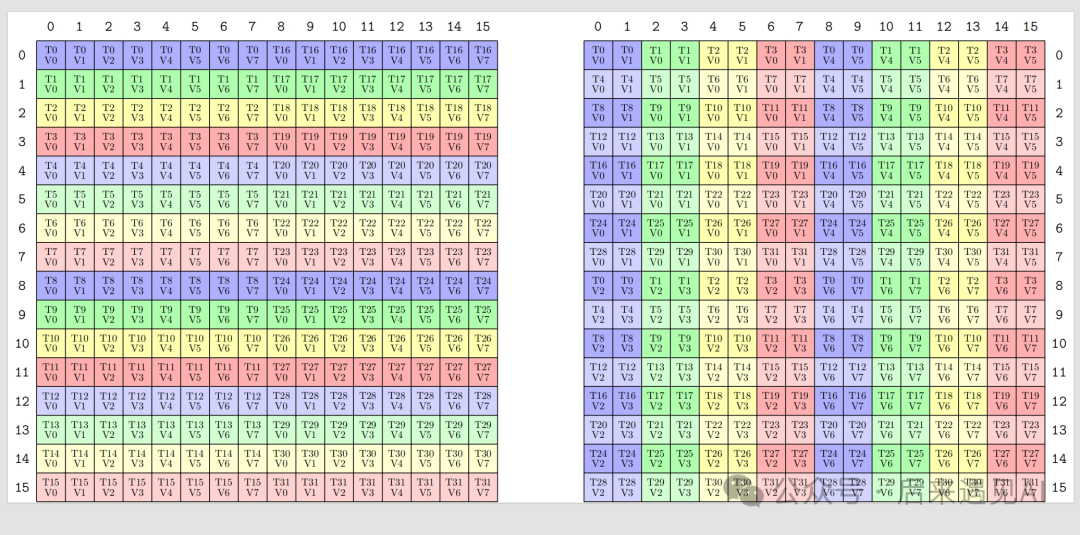
上图中左边是源矩阵,右边是目标矩阵,可以看出其加载过程以及寄存器中持有的元素布局与上面介绍的矩阵 A 完全一致。
类似地,cute 中的结构体 SM75_U32x2_LDSM_N 封装的指令源码如下:
struct SM75_U32x2_LDSM_N
{
...
CUTE_HOST_DEVICE static void
copy(uint128_t const& smem_src,
uint32_t& dst0, uint32_t& dst1)
{
#if defined(CUTE_ARCH_LDSM_SM75_ACTIVATED)
uint32_t smem_int_ptr = cast_smem_ptr_to_uint(&smem_src);
asm volatile ("ldmatrix.sync.aligned.x2.m8n8.shared.b16 {%0, %1}, [%2];\n"
: "=r"(dst0), "=r"(dst1)
: "r"(smem_int_ptr));
#else
CUTE_INVALID_CONTROL_PATH("Trying to use ldmatrix without CUTE_ARCH_LDSM_SM75_ACTIVATED.");
#endif
}
};从 copy 方法可以看出,其对应的指令为 ldmatrix.sync.aligned.x2.m8n8.shared.b16,同样地,我们将其 copy atom 对象对应的 layout 打印出来看一下:
void ldmatrixLayout() {
TiledMMA mmaC = make_tiled_mma(MMA_Atom<SM80_16x8x16_F16F16F16F16_TN>{},
Layout<Shape<_1, _1>>{});
Copy_Atom<SM75_U32x2_LDSM_N, cute::half_t> s2r_atom_B;
TiledCopy s2r_copy_b = make_tiled_copy_B(s2r_atom_B, mmaC);
print_latex(s2r_copy_b);
}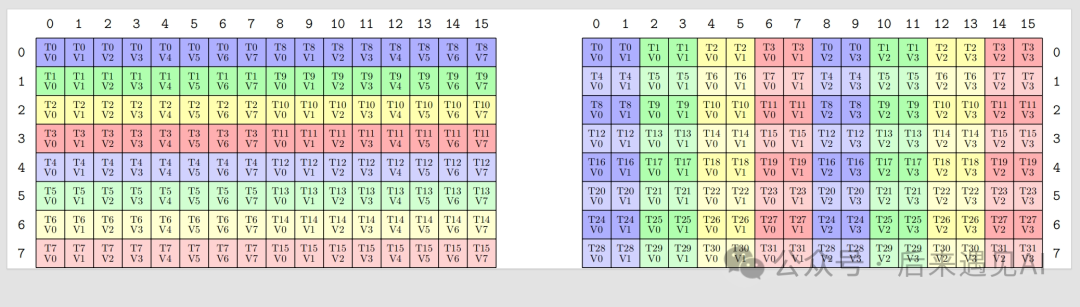
可以发现,上图中的源矩阵和目的矩阵都是一个 [8, 16] 矩阵,与矩阵 B 的形状 [16, 8] 不符,这主要是因为在 cute 中这里对 B 矩阵是按 [n, k] 形状显示的,无伤大雅,其实相当于 [16, 8] 列主序矩阵的一个转置,转置过来看之后寄存器中的元素也与上面介绍的矩阵 B 布局一致。
类似地,cute 中的结构体 SM75_U16x4_LDSM_T 封装的指令源码如下:
struct SM75_U16x4_LDSM_T
{
...
CUTE_HOST_DEVICE static void
copy(uint128_t const& smem_src,
uint32_t& dst0, uint32_t& dst1)
{
#if defined(CUTE_ARCH_LDSM_SM75_ACTIVATED)
uint32_t smem_int_ptr = cast_smem_ptr_to_uint(&smem_src);
asm volatile ("ldmatrix.sync.aligned.x2.trans.m8n8.shared.b16 {%0, %1}, [%2];\n"
: "=r"(dst0), "=r"(dst1)
: "r"(smem_int_ptr));
#else
CUTE_INVALID_CONTROL_PATH("Trying to use ldmatrix without CUTE_ARCH_LDSM_SM75_ACTIVATED.");
#endif
}
};从 copy 方法可以看出,其对应的指令为 ldmatrix.sync.aligned.x2.trans.m8n8.shared.b16,同样地,我们将其 copy atom 对象对应的 layout 打印出来看一下:
void ldmatrixLayout() {
TiledMMA mmaC = make_tiled_mma(MMA_Atom<SM80_16x8x16_F16F16F16F16_TN>{},
Layout<Shape<_1, _1>>{});
Copy_Atom<SM75_U16x4_LDSM_T, cute::half_t> s2r_atom_B;
TiledCopy s2r_copy_b = make_tiled_copy_B(s2r_atom_B, mmaC);
print_latex(s2r_copy_b);
}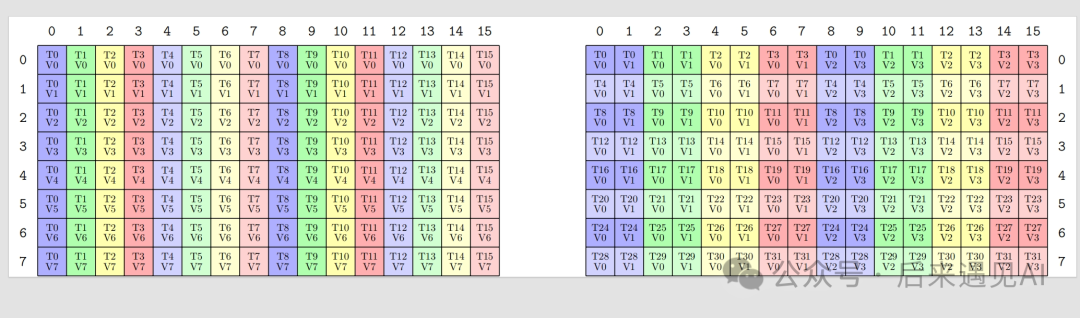
可以发现,上图中的源矩阵和目的矩阵都是一个 [8, 16] 矩阵,与矩阵 B 的形状 [16, 8] 不符,这主要是因为在 cute 中这里对 B 矩阵是按 [n, k] 形状显示的,其实相当于 [16, 8] 行主序矩阵的一个转置,转置过来看之后寄存器中的元素也与上面介绍的矩阵 B 布局一致。
4 stmatrix 指令
上一节介绍了 mma 计算前的加载指令 ldmatrix,主要用于从 shared memroy 加载 A 和 B 矩阵到寄存器用于 mma 计算,本节介绍计算完成后的存储指令 stmatrix,主要用于计算完成后将矩阵 C 或 D 从寄存器存储到 shared memory,下面先来看一下指令语法:
stmatrix.sync.aligned.shape.num{.trans}{.ss}.type [p], r;
.shape = {.m8n8, .m16n8};
.num = {.x1, .x2, .x4};
.ss = {.shared{::cta}};
.type = {.b16, .b8};stmatrix 指令的限定符和参数解释如下:
-
• stmatrix.sync.aligned表示这是一个存储矩阵的指令,自带一个屏障的效果,范围是 warp,即执行线程会等待 warp 内所有的线程执行指令结束再往下执行。warp 中的所有线程必须执行相同的 stmatrix 指令,不允许 warp 内分支发散,否则行为是未定义的。 -
• .shape限定符指定了正在写入的矩阵的维度,m8n8表示一次加载一个[8, 8]矩阵。 -
• .num表示总共需要写入多少个形状为.shape的矩阵,以m8n8为例,则.x1表示加载矩阵维度为[8, 8],.x2表示最终加载矩阵的维度为[16, 8],.x4表示最终加载矩阵的维度为[16, 16]。 -
• .trans是一个可选参数,表示是否需要将矩阵转置。 -
• .shared{::cta}是针对线程块集群和分布式共享内存的场景,本文不做讨论。 -
• .type指定了矩阵的数据类型。 -
• r是寄存器。 -
• p是 shared memory 空间中的目标地址,如果没有指定.shared{::cta}则使用通用寻址。
同样地,我们还是以一个形状为 m16n8k16 的半精度矩阵乘法为例来解释一下 stmatrix 的执行逻辑。
首先 stmatrix 是一个 warp 级别的数据加载指令,并且是按行进行写入 shared memory,比如以 m8n8.x1为例(即一个[8, 8]矩阵),被分为 8 行写入,这 8 个行可以不连续,也就是说这个[8, 8]矩阵的主维度可以不是 8(比如写入一个[16, 16]矩阵中的一个子矩阵),那么就需要 8 个共享内存空间的地址对应每行的首地址,这 8 个目标地址需要依次赋给线程 0-7 的目标地址p参数。注意,这并不意味着 warp 内的其他 16 个线程可以不执行这个指令,其他线程一样执行指令并给 p 赋值,只是赋的值不会被使用而已。而对于m8n8.x2和m8n8.x4的场景,每行的首地址需要分别赋给线程 0-15 和线程 0-31 的目标地址p 参数,如下图所示:

可以看出,stmatrix 指令和 ldmatrix 指令的用法几乎一致,二者是一个相反的过程,但是要注意的是 ldmatrix 指令从 sm_75 开始就被支持,而 stmatrix 指令需要在 sm_90 以上的架构才能使用。
还是以 m8n8.x1 为例,虽然只有前 8 个线程中的目标地址 p 参数被赋了有效值,但其他线程中的寄存器也会参与此次写入,一行 8 个 half 元素被连续的 4 个线程写入,每个线程写入 2 个元素,对应一个寄存器。也就是说,首地址赋给线程 0 的这一行元素,从线程 0-3 的寄存器中被写入到 shared memory,首地址赋给线程 1 的一行元素,从线程 4-7 的寄存器中被写入到 shared memory,依次类推。

而对于 m8n8.x2 和 m8n8.x4 场景,不过就是重复写入几次 m8n8 矩阵,并将元素依次从 warp 内线程的后续寄存器写入 shared memory 罢了。
4.1 写入矩阵 C 或 D
不难发现,上面的线程寄存器中持有的元素在原矩阵中的位置正好与 mma 指令的矩阵 C 和 D (非转置)对应起来。因此,对于矩阵 C[16, 8] 的加载方式,我们可以通过如下代码实现,假设矩阵 C 在 shared memory 中是行主序排布:
#define STMATRIX_X2(addr, R0, R1) asm volatile("stmatrix.sync.aligned.x2.m8n8.shared.b16 [%0], {%1, %2};\n" : : "l"(__cvta_generic_to_shared(addr)), "r"(R0), "r"(R1))
STMATRIX_X2(s_c + lane_id / 4, RC[0], RC[1]);在计算地址的时候,要注意一点,C 矩阵中子矩阵的排布是列主序的,这也是为了适配 mma 指令对矩阵 C 的要求,由于笔者手头暂无 Hopp 架构的 GPU,就不验证了。
5 movmatrix 指令
movmatrix 指令是从 sm_75 开始引入的 PTX 指令,主要用于 warp 内矩阵转置操作,通过 warp 内寄存器数据交换实现。指令语法如下:
movmatrix.sync.aligned.shape.trans.type d, a;
.shape = {.m8n8};
.type = {.b16};movmatrix 指令的限定符和参数解释如下:
-
• movmatrix.sync.aligned表示这是一个矩阵相关的数据移动指令,自带一个屏障的效果,范围是 warp,即执行线程会等待 warp 内所有的线程执行指令结束再往下执行。warp 中的所有线程必须执行相同的 movmatrix 指令,不允许 warp 内分支发散,否则行为是未定义的。 -
• .shape限定符指定了正在写入的矩阵的维度,m8n8表示一次加载一个[8, 8]矩阵。 -
• .trans表示该指令是要做矩阵转置。 -
• .type指定了矩阵的数据类型。 -
• d是目标寄存器。 -
• a是源寄存器。
前面说过,在计算 mma 之前,warp 内各个线程均持有了待计算矩阵的几个元素,存储在线程对应的寄存器中,假设目前各个线程持有的矩阵元素存储在寄存器 RA 中,组成的矩阵如下所示:

从上图可以看出,其实这个元素布局跟正常未转置的矩阵 A 一样,使用 movmatrix 指令可以将上面的元素布局变更为下图所示。

movmatrix 指令比较简单,因为目前仅支持 m8n8 且一次只支持转置一个矩阵,数据类型也仅支持 b16,其作用比较单一就是矩阵转置,通常用于在计算 mma 之前将对应的矩阵做转置以适配 mma 指令参数的需要,具体用法如下:
#define MOVMATRIX(D0, A0) asm volatile("movmatrix.sync.aligned.m8n8.trans.b16 %0, %1;\n" : "=r"(D0) : "r"(A0))
uint32_t RA;
uint32_t RB;
...
MOVMATRIX(RB, RA);movmatrix 指令除了在 mma 中使用以外,也可以用于矩阵转置任务,给矩阵转置工作提供了一个新的思路,笔者下面提供了一个简单的示例,以供参考。
#include <cstdint>
#include <cfloat>
#include <assert.h>
#include <cuda_runtime.h>
#define LDST128BITS(value) (reinterpret_cast<float4 *>(&(value))[0])
#define LDST32BITS(value) (reinterpret_cast<half2 *>(&(value))[0])
#define LDMATRIX(R0, addr) asm volatile("ldmatrix.sync.aligned.x1.m8n8.shared.b16 {%0}, [%1];\n" : "=r"(R0) : "l"(__cvta_generic_to_shared(addr)))
#define MOVMATRIX(D0, A0) asm volatile("movmatrix.sync.aligned.m8n8.trans.b16 %0, %1;\n" : "=r"(D0) : "r"(A0))
__host__ __device__ __inline__ int div_ceil(int a, int b) {
return (a + b - 1) / b;
}
__global__ void mov_kernel(half* A, half* B, const uint32_t M, const uint32_t K) {
constuint32_t warp_id = threadIdx.x >> 5;
constuint32_t warp_col = warp_id % 2;
constuint32_t warp_row = warp_id / 2;
constuint32_t lane_id = threadIdx.x & 0x1f;
// 源矩阵 warp 级偏移量
constuint32_t src_offset = (blockIdx.y * 16 + warp_row * 8) * K + (blockIdx.x * 16 + warp_col * 8);
// 目标矩阵 warp 级偏移量
constuint32_t dst_offset = (blockIdx.y * 16 + warp_row * 8) + (blockIdx.x * 16 + warp_col * 8) * M;
constuint32_t smem_warp_offset = warp_row * 8 * 16 + warp_col * 8;
__shared__ half s_a[16 * 16];
__shared__ half s_b[16 * 16];
// 8 个线程每个线程 load 一行
if (lane_id < 8) {
LDST128BITS(s_a[smem_warp_offset + lane_id * 16]) = LDST128BITS(A[src_offset + lane_id * K]);
}
__syncthreads();
uint32_t RA;
uint32_t RB;
LDMATRIX(RA, s_a + smem_warp_offset + (lane_id % 8) * 16);
MOVMATRIX(RB, RA);
int store_smem_b_row = warp_row * 8 + lane_id / 4;
int store_smem_b_col = warp_col * 8 + (lane_id % 4) * 2;
LDST32BITS(s_b[store_smem_b_row * 16 + store_smem_b_col]) = LDST32BITS(RB);
__syncthreads();
// 8 个线程每个线程 load 一行
if (lane_id < 8) {
LDST128BITS(B[dst_offset + lane_id * M]) = LDST128BITS(s_b[smem_warp_offset + lane_id * 16]);
}
}
void transpose_naive(half* A, half* B, const uint32_t M, const uint32_t K) {
assert(M % 16 == 0 && K % 16 == 0);
dim3 block(128);
dim3 grid(div_ceil(K, 16), div_ceil(M, 16));
mov_kernel << <grid, block >> > (A, B, M, K);
}上面的代码是一个 warp 角度的代码,从 A 中读取当前 warp 分片的 m8n8 矩阵到 s_a 然后使用 lamatrix 指令读取到寄存器 RA,再使用 movmatrix 指令转置后存储到寄存器 RB,将 RB 写回到 s_b 再写回到 B 矩阵。
6 小结
本文将聚焦矩阵乘加运算的四个核心指令(ldmatrix、mma、stmatrix、movmatrix),解析其运作机制与优化策略,同时结合 cute 库的封装实现进行对照阐释。
-
• ldmatrix 指令用于将矩阵从 shared memory 加载到寄存器 -
• mma 指令用于矩阵乘加操作 -
• stmatrix 指令用于将矩阵从寄存器写回 shared memory,与 ldmatrix 正好相反 -
• movmatrix 指令用于 warp 内寄存器中矩阵转置
(文:极市干货)