CUTLASS CuTe GEMM细节分析（二）——TiledCopy与cp.async

Prologue

在上一篇文章(https://zhuanlan.zhihu.com/p/702818267)中，我们分析了从Shared Memory向Registers拷贝矩阵的ldmatrix指令。

流水线技术是一种能够掩盖访存延迟，提升硬件资源利用率的优化技术。基于CuTe的GEMM将SM80的cp.async指令进行封装并扩展成TiledCopy，实现了Global Memory到Shared Memory的异步拷贝，在执行异步拷贝的同时，利用TensorCore完成MMA计算，最终实现了数据加载->计算的流水线。

本文尝试从另外一个角度——访存合并——深入理解TiledCopy，希望这些内容能够对大家的Kernel性能调优工作有所帮助。

TiledCopy参数的理解

我们先从一个非常简单的TiledCopy入手：

    using g2r_copy_op = UniversalCopy<T>;    using g2r_copy_traits = Copy_Traits<g2r_copy_op>;    using g2r_copy_atom = Copy_Atom<g2r_copy_traits, T>;    using G2RCopy = decltype(make_tiled_copy(g2r_copy_atom{},                        Layout<Shape<_16, _8>, Stride<_8, _1>>{},                        Layout<Shape<_1, _4>>{}));    print(G2RCopy{})

将模板参数T指定为half_t类型，并利用CuTe的print函数打印这个TiledCopy的实例，得到如下结果：

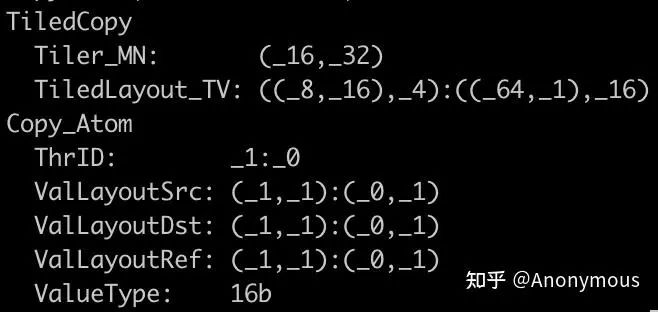
我们重点分析输出中的Tiler_MN和TiledLayout_TV这两个参数的意义，以及它们与make_tiled_copy函数参数的关系。

Tiler_MN

Tiler_MN代表TiledCopy执行一次copy时，操作的Src/Dst Tensor的Shape，也就是说，Src/Dst Tensor的Shape是Tiler_MN即可，TiledCopy并不会对Stride做强制的要求。

在真实的GEMM计算任务中，存储于Global Memory的输入矩阵可能是Row-Major的，也可能是Column-Major的。我们的TiledCopy进行一次copy操作时，通常仅仅是拷贝大的输入矩阵中的一个小分块，只要这个小分块的Shape与TiledCopy中的Tiler_MN一致，就可以使用这个TiledCopy一次性完成这个小分块的拷贝动作，而不需要关心这个小分块的Stride是多少。通常，这些小分块的Layout在不同场景下可能会差异巨大。例如，对于一个4096 x 4096的矩阵，以Row-Major存储时，位于其中间的一个(16, 64)的分块的步长是(4096, 1)，而不是(64, 1)，如果是以Column-Major存储，则这个分块的步长是(1, 4096)，而不是(1, 16)。我们甚至可能会遇到更复杂的复合Layout，但这并不影响TiledCopy完成它的功能，因为它仅需分块的Shape与其Tiler_MN一致即可。

可以看到，构造TiledCopy并不依赖于它将要操作的Src/Dst Tensor的信息。换句话说，TiledCopy的构造与Src/Dst Tensor的Layout解耦。这是一种模块化的实现，对于软件的可扩展性具有积极的作用。

那么Tiled_MN所表达的Shape又是如何构造的呢？

Tiled_MN的构造严格依赖于CuTe的Layout代数理论，在本文中，我并不打算直接基于Layout代数介绍Tiled_MN的构造，因为这有失于本文的主旨——以相对通俗的方式理解TiledCopy，关于Layout代数，读者可以参考CuTe的官方教程(https://github.com/NVIDIA/cutlass/blob/main/media/docs/cute/02_layout_algebra.md)。

Tiled_MN的构造依赖于make_tiled_copy函数中ThrLayout参数和ValLayout参数。ThrLayout表示我们如何从执行单元的层面对Copy_Atom进行扩展，而ValLayout则表示每个执行单元所拷贝的Tensor分块的Shape。

还是以上文代码为例进行说明，Copy_Atom所表达的“原子能力”为：一个执行单元（CUDA Thread）能够完成一个1个元素的拷贝。首先，我们定义执行单元所拷贝的Tensor分块为(1, 4)，即ValLayout。接下来，我们将执行单元扩展为16×8个（ThrLayout的Shape），即(1×16, 4×8)–>(16, 32)，最终得到TiledCopy一次拷贝能够操作的Shape。

细心的同学可能会发现，ThrLayout并未使用默认的Stride，而是指定了一个Stride<_8, _1>。这个Stride所表达含义就是当前线程块中的线程与16×8个执行单元的对应关系，这个值也会影响TiledLayout_TV。那么具体是如何影响的呢？

TiledLayout_TV

首先，我们以一种相对通俗的方式解释Stride<_8, _1>是如何控制线程的分布的。

Layout<Shape<_16, _8>, Stride<_8, _1>>代表16×8个执行单元是以行主序的形式排布的，也就是说，Thread ID在行方向上连续递增，在列方向上以8为步长递增，如图所示：

图2展示了前16个Thread负责的数据分块，其中，每一个线程负责拷贝Tiler_MN一行上连续的4个元素（由(1, 4)简化而来）。

基于此，我们便可以最终确定TileCopy执行copy时，每一个Thread所负责的具体Tensor分块在哪。但与此同时，也引出了两个问题：

本节我们先来分析第二个问题。

TiledLayout_TV是一个复合的Layout，Layout本质上是一个映射，它能够将一个由整数构成的坐标转换为一个标量offset。TiledLayout_TV所表达的含义为：给定一个Thread的ID，以及这个Thread所负责的Tensor分块中某个元素的坐标，返回这个元素在Tiled_MN中的坐标。

等等，Layout输出不是一个标量offset吗？为什么返回的是一个坐标？在CuTe Layout官方文档(https://github.com/NVIDIA/cutlass/blob/main/media/docs/cute/01_layout.md)中给出了说明，对于一个标量，我们可以根据Shape各个维度的大小，将一个标量值转换为一个坐标。例如，对于Shape(3, 3)，给定一个值5，它可以转换为坐标(2, 1)。

我们结合一个具体的例子来说明TiledLayout_TV的作用。假设，TiledLayout_TV为上文中的((8, 16), 4):((64, 1), 16)，我们想知道ID为9的Thread，它拷贝的Tensor分块中，坐标为(0, 2)的元素，对应Tiler_MN中的坐标是多少？

因此，对于Thread 9这个线程来说，它拷贝的Tensor分块中坐标为(0, 2)的元素位于Tiler_MN的(1, 6)位置处。事实上，Thread 9负责Tiler_MN上(1, 4:8)这个分块。

可以看到Layout不仅可以表达复杂的Tensor元素分布，它甚至可以将多个定义域整合在一起，用于表达某种更复杂的映射关系。CuTe的核心即为Layout及其代数理论，但在真实场景中我们可能并不需要过多的关心Layout代数的细节，因此不建议大家花费过多时间在研究Layout相关理论上。若读者对深层的Layout代数理论感兴趣，可以参考CUTLASS CuTe官方的系列教程(https://github.com/NVIDIA/cutlass/tree/main/media/docs/cute)。

访存的连续性

根据上文的内容，我们现在明确了两件事：

因此，我们需要注意访存连续性的问题，仍然是以上文的代码为例，TiledCopy拷贝Shape为(16, 32)的Tensor分块，其中每8个连续的Thread负责拷贝一行中32个元素，每个Thread拷贝4个元素。

通常情况下，拷贝的Tensor分块都是一个更大的Tensor的子块，假定我们的Tensor是一个二维矩阵，大小为4096 x 4096，Layout为Row-Major。那么每个(16, 32)的Tensor分块的Stride为(4096, 1)，此时，可以观察到，对于一共128个线程来说，每8个线程访问连续的32个元素，每个线程访问连续的4个元素，此时可以使用向量化SASS指令进行访问，如下所示（表格中的值代表地址offset）：

(_16,_32):(_4096,_1)          0       1       2       3       4       5       6       7       8       9      10      11      12     +-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+ 0  |     0 |     1 |     2 |     3 |     4 |     5 |     6 |     7 |     8 |     9 |    10 |    11 | ......    +-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+ 1  |  4096 |  4097 |  4098 |  4099 |  4100 |  4101 |  4102 |  4103 |  4104 |  4105 |  4106 |  4107 | ......    +-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+ 2  |  8192 |  8193 |  8194 |  8195 |  8196 |  8197 |  8198 |  8199 |  8200 |  8201 |  8202 |  8203 | ......    +-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+ 3  | 12288 | 12289 | 12290 | 12291 | 12292 | 12293 | 12294 | 12295 | 12296 | 12297 | 12298 | 12299 | ......    +-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+-------+ 4  | ......    +------- 5  | ......

如果矩阵是以Column-Major的形式存储的（Stride为(1, 4096)），那么情况就会变差：

(_16,_32):(_1,_4096)           0        1        2        3        4        5        6        7        8    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 0  |      0 |   4096 |   8192 |  12288 |  16384 |  20480 |  24576 |  28672 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 1  |      1 |   4097 |   8193 |  12289 |  16385 |  20481 |  24577 |  28673 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 2  |      2 |   4098 |   8194 |  12290 |  16386 |  20482 |  24578 |  28674 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 3  |      3 |   4099 |   8195 |  12291 |  16387 |  20483 |  24579 |  28675 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 4  |      4 |   4100 |   8196 |  12292 |  16388 |  20484 |  24580 |  28676 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 5  |      5 |   4101 |   8197 |  12293 |  16389 |  20485 |  24581 |  28677 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 6  |      6 |   4102 |   8198 |  12294 |  16390 |  20486 |  24582 |  28678 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 7  |      7 |   4103 |   8199 |  12295 |  16391 |  20487 |  24583 |  28679 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 8  |      8 |   4104 |   8200 |  12296 |  16392 |  20488 |  24584 |  28680 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+ 9  |      9 |   4105 |   8201 |  12297 |  16393 |  20489 |  24585 |  28681 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+10  |     10 |   4106 |   8202 |  12298 |  16394 |  20490 |  24586 |  28682 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+11  |     11 |   4107 |   8203 |  12299 |  16395 |  20491 |  24587 |  28683 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+12  |     12 |   4108 |   8204 |  12300 |  16396 |  20492 |  24588 |  28684 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+13  |     13 |   4109 |   8205 |  12301 |  16397 |  20493 |  24589 |  28685 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+14  |     14 |   4110 |   8206 |  12302 |  16398 |  20494 |  24590 |  28686 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+15  |     15 |   4111 |   8207 |  12303 |  16399 |  20495 |  24591 |  28687 |  ......    +--------+--------+--------+--------+--------+--------+--------+--------+--------+

此时，每一个线程内负责拷贝的4个元素在地址上就是不连续的，并且，相邻的8个线程访问的地址也不再连续。这种模式下，在一个warp内，仅存在一种连续性——间隔为8的线程访问相邻的元素，例如，线程0，8，16，24分别访问offset为0，1，2，3的元素。

对于这种Column-Major的情况，我们最好使用上文提供的TiledCopy的“转置形式”：

    using g2r_copy_op = UniversalCopy<T>;    using g2r_copy_traits = Copy_Traits<g2r_copy_op>;    using g2r_copy_atom = Copy_Atom<g2r_copy_traits, T>;    using G2RCopy = decltype(make_tiled_copy(g2r_copy_atom{},                        Layout<Shape<_8, _16>, Stride<_1, _8>>{},                        Layout<Shape<_4, _1>>{}));

关于这种TiledCopy的访存连续性分析，读者可自行完成。

cp.async

在reed大佬的介绍GEMM流水线(https://zhuanlan.zhihu.com/p/665082713)的文章中，已经详细的介绍了cp.async指令的用法，本文不再赘述。本文将会描述如何基于cp.async构造TiledCopy。

我们将会结合以下示例说明如何基于cp.async构造TiledCopy：

    using g2s_copy_op = SM80_CP_ASYNC_CACHEGLOBAL<cute::uint128_t>;    using g2s_copy_traits = Copy_Traits<g2s_copy_op>;    using g2s_copy_atom = Copy_Atom<g2s_copy_traits, half_t>;    using G2SCopyA = decltype(make_tiled_copy(g2s_copy_atom{},                        make_layout(make_shape(Int<16>{}, Int<8>{}),                                    make_stride(Int<8>{}, Int<1>{})),                        make_layout(make_shape(Int<1>{}, Int<8>{}))));  // Copy Tile: (16, 64)

ValLayout的选择

定义Copy_Atom时，我们指定了拷贝的元素类型为half_t，由于我们使用向量化的cp.async指令执行拷贝，且向量的大小为128bit，即8个half_t类型的元素，那么此时Copy_Atom表达的原子能力就不再是一个Thread只能拷贝1个元素，而是一个Thread能够拷贝8个元素。

因此，当我们调用make_tiled_copy时，定义的ValLayout的size必须是8的整数倍，比如，(1, 8)，(2, 4)，(1, 16)都是合法的ValLayout，代表在真实的拷贝场景中，一个Thread通过一次或多次Copy_Atom的“原子能力”完成拷贝。

Src/Dst Tensor Layout的限制

虽然TiledCopy的构造并不依赖于Src/Dst Tensor的Layout，但向量化的cp.async指令拷贝的是地址连续的16Byte（128bit）的向量，这就对Src/Dst Tensor的Layout做出了一些限制。

在上文的例子中，每个Thread拷贝Shape为(1, 8)的Tensor分块，对应到Src/Dst Tensor时，每个(1, 8)的Tensor分块中的元素必须是连续的，也就是说，Shape为8的这个维度，对应的Stride必须是1，否则就会报错，因此，对于这个TiledCopy，我们通常使用它拷贝Row-Major的矩阵分块，因为这个(16, 64)的分块进一步拆分为多个(1, 8)的子块时，在行方向上都是连续的。如果我们使用这个TiledCopy去拷贝Column-Major的矩阵分块，在编译时就会报错：Copy_Traits: src failed to vectorize into registers. Layout is incompatible with this CopyOp.

对于Column-Major的分块，可以使用上述示例的“转置版”：

    using g2s_copy_op = SM80_CP_ASYNC_CACHEGLOBAL<cute::uint128_t>;    using g2s_copy_traits = Copy_Traits<g2s_copy_op>;    using g2s_copy_atom = Copy_Atom<g2s_copy_traits, half_t>;    using G2SCopyA = decltype(make_tiled_copy(g2s_copy_atom{},                        make_layout(make_shape(Int<16>{}, Int<8>{}),                                    make_stride(Int<1>{}, Int<16>{})),                        make_layout(make_shape(Int<8>{}, Int<1>{}))));  // Copy Tile: (128, 8)

访存连续性简析

对于上述代码示例，我们可以分析出，128个线程中每8个连续的线程访问连续的64个half_t元素，每个线程通过一个128bit的向量指令访问连续的8个元素。8个线程共访问连续的128Byte的数据，正好对应于GPU的Cache Line大小。我们从一个warp的角度来看，一个warp以一个整体执行cp.async时，恰好能访问4个Cache Line，4个Cache Line的数据没有任何的冗余，这种访存模式能够有效的利用HBM/L2带宽。

但如果我们换成这种TiledCopy：

  using g2s_copy_op = SM80_CP_ASYNC_CACHEGLOBAL<cute::uint128_t>;  using g2s_copy_traits = Copy_Traits<g2s_copy_op>;  using g2s_copy_atom = Copy_Atom<g2s_copy_traits, half_t>;  using G2SCopyA =      decltype(make_tiled_copy(g2s_copy_atom{},                               make_layout(make_shape(Int<32>{}, Int<4>{}),                                           make_stride(Int<4>{}, Int<1>{})),                               make_layout(make_shape(Int<1>{}, Int<8>{}))));

这种情况下，128个线程中每4个连续的线程访问32个half_t元素，大小为64Byte，只有半个Cache Line的大小。由于从L2到L1/Shared Memory数据传输粒度为Cache Line，那么这种情况就会浪费一半的L2缓存带宽，有可能会造成性能问题。

Epilogue

本文从参数意义和访存连续性这两个角度深入的分析了TiledCopy。目前，我们已经了解了Global -> Shared以及Shared -> Register的copy抽象，Shared Memory作为中转Storage，其Layout抽象对于这两个过程都具有重要的意义，我们将会在后续的文章中进一步分析Swizzle抽象及其参数设置。