太长不看版

LLM 后训练量化过程的一个有效改进方案。

在大语言模型的量化技术中，后训练量化 (Post-Training Quantization, PTQ) 因其在压缩效率高，成本效益明显而研究很多。现有的 LLM 后训练量化方法限制了优化的范围，以缩放预量化权值和后量化权值之间的转换。这种约束导致量化后出现重大错误，尤其是在低比特量化配置中。

本文提出在 PTQ (AffineQuant) 中使用等价仿射变换 (Affine Transformation) 进行直接优化。这种方法扩展了优化范围，显著减少了量化误差。此外，通过使用相应的逆矩阵，可以确保 PTQ 的预量化输出和后量化输出之间的等价性，从而保持其效率和泛化能力。

为了确保优化过程中变换的可逆性，本文进一步引入了一种渐进掩码的优化方法。该方法最初侧重于优化对角元素并逐渐扩展到其他元素。这种方法与 Levy-Desplanques 定理一致，理论上确保了变换的可逆性。因此，在不同的数据集上，不同 LLM 显而易见地取得了性能改进。值得注意的是，当使用非常低比特进行量化时，改进最为明显，使其能够在边缘设备上部署大模型。

实验结果上，作者在 W4A4 量化的 LLaMA2-7B 模型上获得了 15.76 (OmniQuant 中 18.02) 的 C4 困惑度，而无需开销。在 Zero-Shot 任务上，AffineQuant 在 LLaMA-30B 使用 W4A4 量化时，平均达到了 58.61% 的精度 (OmniQuant 中 56.63)，为 LLM 的 PTQ 提供了新的 sota 基准。

本文目录

1 AffineQuant：LLM 的仿射变换量化
(来自厦门大学纪荣嵘团队，ByteDance)
1 AffineQuant 论文解读
1.1 AffineQuant 研究背景
1.2 AffineQuant：为权重和激活进行仿射变换
1.3 渐进式掩码
1.4 AffineQuant 的效率
1.5 实验设置
1.6 实验结果

1 AffineQuant：LLM 的仿射变换量化

论文名称：AffineQuant: Affine Transformation Quantization for Large Language Models (ICLR 2024)

论文地址：

http://arxiv.org/pdf/2403.12544

代码链接：

http://github.com/bytedance/AffineQuant

1.1 AffineQuant 研究背景

大型语言模型 (LLM) 由于其令人印象深刻的性能而受到越来越多的关注。然而，emergent logical reasoning 能力仅存在于一定大小阈值以上的模型中。因此，LLM 的训练和推理效率需要仔细考虑。具体来说，LLM 在移动和边缘设备上进行推理有很多潜在价值。量化被认为是模型压缩方法中最有前途的方法之一。特别是，它将 weight 和 activation 映射到低比特表示，有效地减少了模型的显存使用。此外，优化低比特操作符的编译显著提高了它们的效率，加速模型推理。

同时，由于训练 LLM 需要大量计算资源和高质量数据，通过模型微调实现量化具有挑战性。因此，研究界越来越强调无训练算法，称为后训练量化 (PTQ)。PTQ 允许以很少的校准数据进行有效优化。但是这种方法也会导致显著的性能下降，尤其是在小模型或低比特的场景中。

很多 PTQ 方法采用等价变换。如图 1 所示，AWQ[1]通过优化统计数据来增强尺度计算，并引入预量化和后量化特征图之间的均方误差损失作为 LLM 中第一次的优化指标。Omniquant[2]引入了可学习的 scale 和 shift 参数来增强优化。在更高的维度中，等效量化的概念也受到关注。RPTQ[3]通过对 activation 的列进行排序来实现每个集群的 activation 量化。重新排序可以通过将 scale 从向量转换为矩阵形式来在数学上表示，其中每一行和列对应于单个尺度值。这种转换以等效的方式有效地重新排列 activation 的列和 weight 的行。

总之，等效量化的演变从手动设计到梯度优化，从低维到高维，以及从单尺度合并到多个操作的组合。等效量化在2个主要方面具有优势：1) 保证预量化输出和后量化输出之间的一致性，进而通过优化等价变换参数可以有效地缓解量化噪声。这与后训练量化的概念一致，其中等价变换充当噪声改进的媒介。2) 不同类型的等价变换相互正交。直观地说，引入每种新型等价变换扩展了参数优化空间，从而提高了性能。

因此，本文提出了一种等效仿射变换的算法。具体来说，将仿射变换矩阵左乘到线性层中的权重，并将逆矩阵与激活右乘。在均方误差损失的指导下，优化仿射变换矩阵。与其他算法相比，损失始终较低。此外，作者在优化过程中探讨了矩阵的可逆性。Levy-Desplanques 定理表明严格对角支配矩阵 (Strictly Diagonally Dominant Matrix) 是可逆的。为了确保仿射变换矩阵严格对角支配，作者采用对角初始化和渐进掩码的方法。这样一来，高维矩阵的优化就可以使用校准集，通过渐进优化的过程得到。在推理效率方面，本文方法在矩阵合并后与其他方法一致。

1.2 AffineQuant：为权重和激活进行仿射变换

定义伪量化函数如下：

其中 分别是量化步长，零点和比特数。 是舍入运算。如图 1 所示，AffineQuant 给权重矩阵 左乘一个仿射变换矩阵 ，以更好地将权重分布与量化函数 对齐。扩展优化空间使转换后的权重中的量化误差更小，从而降低困惑度。同时，将仿射变换矩阵 的逆与激活值 右乘，以保持激活和权重之间的矩阵乘法输出不变性。对于单个线性层，AffineQuant 优化问题如下：

AffineQuant 结合了 AWQ 和 SmoothQuant 的本质，其中矩阵 的主对角元素由 weight 和 activation 的统计量计算得到。如果是专门更新 的对角元素，那就与 OmniQuant 对齐了。RPTQ 中使用的重新排序矩阵是仿射变换矩阵 的子集，当 的每一行和列仅出现1—次时。总之，AffineQuant 包含以前的各种量化算法，扩大了权重分布 的优化可能性。

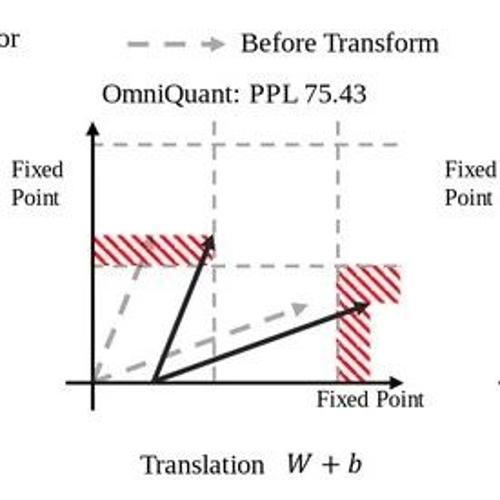
在图 1 中，设权重矩阵 有 2 个输出通道和输入通道。缩放因子，平移因子和仿射变换矩阵分别表示为 。作者根据输出通道将权重矩阵划分为 2 个向量 。缩放变换 均匀地缩放 的每个元素。平移变换 沿不同轴移动 。仿射变换 允许对 进行任意重定位。然而，缩放和平移变换限制了它们将 中的维度映射到相邻 fixed point 的能力。相比之下，仿射变换保证了向量中所有维度收敛到 fixed point。换句话说，仿射变换将 weight 的分布与式 2 中量化函数 引入的噪声对齐，降低量化误差。值得注意的是，将仿射变换矩阵归一化为 ，其中矩阵 的每一行的范数为1，将 转换为标准旋转矩阵。旋转矩阵 在保留权重的大小的同时旋转权重的输出通道。比例因子 在旋转向量上执行缩放。因此，仿射变换矩阵 结合了缩放和旋转等效变换，并且与平移变换正交。

困惑度 (ppl) 与交叉熵 (CE) 损失呈指数关系，与量化前后输出激活均方误差正相关。因此，可以通过优化量化前后的均方误差来实现优化困惑度：

在大语言模型量化中，AffineQuant 的优化目标如下：

其中 是第 个 Transformer Block。 分别是等价变换后的 activation，weight 和 bias。将仿射变换和平移变换结合起来，并使用 Transformer Block 输出的均方误差作为优化目标。

图 2 说明了 LLAMA7B 和 OPT-1.3B 最后一个 Transformer Block 的均方误差损失优化。值得注意的是，与 OmniQuant 相比，AffineQuant 的初始损失较低，因为仿射变换矩阵的优越性能。此外，与 OmniQuant 相比，AffineQuant 在最后一个 Block 中表现出更快的损失收敛和更优越的整体优化性能。这些结果表明了可逆矩阵优化的巨大潜力。

1.3 渐进式掩码

在优化过程中，需要对仿射变换矩阵求逆。但是，式 4 的目标函数中不包括任何约束，以确保矩阵保持满秩。因此，如何在优化过程中保持矩阵可逆。首先，作者定义了一个严格的对角支配矩阵，如下所示：

定义 1 [严格对角支配矩阵 (Strictly Diagonally Dominant Matrix)] 如果每个对角元素的绝对值大于相应行中剩余元素的绝对值之和，则认为矩阵 A 严格对角支配。具体来说，

Levy-Desplanques 定理[4]确定所有严格对角支配矩阵 (Strictly Diagonally Dominant Matrix) 都是可逆的。

作者先对仿射变换矩阵只初始化其对角元素，其余置为 0，确保它最初严格对角支配。虽然在优化器中使用二阶动量和较低的学习率可以帮助满足 Levy-Desplanques 定理的要求，但随着模型大小的增加，大型仿射变换矩阵的优化仍然面临不稳定的挑战。

为了确保仿射变换矩阵在优化过程中保持严格对角支配，作者提出引入了一种渐进式掩码的方法，如图 3 所示。在每个优化块开始时，作者冻结除主对角线上的元素之外的所有元素。随着优化的进行，逐步解冻主对角线附近的元素。最终，所有矩阵元素都变成可学习的。这种冻结机制，称为 Gradual Mask (GM)，定义如下：

\beginequation} GM_{ij}= \left{ \begin{array}{ll} 1 & i=j, \ \alpha & 0<i-j| \leq \frac{et}\times hidden~size, \ 0 & otherwise, \ \end{array} \right. \end{equation} \tag{6}\begin{equation} GM_{ij}= \left{ \begin{array}{ll} 1 & i=j, \ \alpha & 0<i-j| \leq \frac{e{t}\times hidden~size, \ 0 & otherwise, \ \end{array} \right. \end{equation} \tag{6}

其中， 是掩码矩阵的第 行，第 列元素。 是目标 epoch。 是当前 Epoch。hidden size 是仿射变换矩阵的维度。 是 stability factor。在注意力模块中，作者在每个注意力头中应用 GM 。GM 是一种学习率调节器，通过与矩阵 的元素点积来实现。具体来说， 矩阵对优化过程的影响可以分为两个方面。在这里，作者展示了合并 后矩阵 的优化过程：

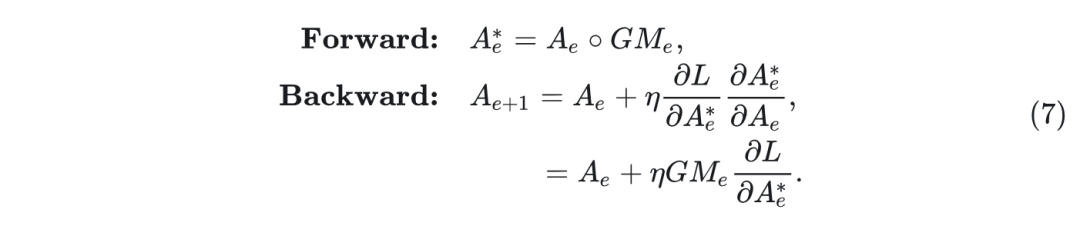
其中， 是 Hadamard 积。 和 分别是 Epoch 中的矩阵 和 Gradual Mask（GM）矩阵。 是矩阵 的学习率。 是优化损失。当 stability factor 小于 1 时，GM 矩阵在前向传播过程中有效地减小了矩阵 中非主对角元素的大小。这确保了 在优化过程中稳定存在逆矩阵。

就像 Levy－Desplanques 定理要求的那样。在反向传播中，GM 影响学习率 ，从而抑制矩阵 中非主对角元素的更新速率。因此，GM 对 的影响确保矩阵 保持严格对角支配，满足 Levy－ Desplanques 定理。值得注意的是，当 接近 0 时，优化过程稳定收敛并等效于 OmniQuant。AffineQuant 中的渐进式掩码确保了仿射变换矩阵的严格对角支配的属性。

1.4 AffineQuant 的效率

优化效率

PyTorch 的线性代数库提供了 float 和 double 的矩阵求逆计算。因此，在整个优化过程中，作者将模型的精度保持为 float 或 double。此外，由于计算机的数值精度限制，矩阵逆的近似计算可能包含错误。

推理效率

作者将仿射变换矩阵与其他层集成在一起。随后，对网络执行半精度推理。对于所有线性层，将仿射变换矩阵与 weight 和 bias 参数合并。此外，对于 LayerNorm 之后的仿射矩阵，只优化对角元素，然后进行 weight 和 activation 的量化。这样是为了将仿射矩阵与 LayerNorm 的权重和方差合并。因此，AffineQuant 可以在推理中不引入任何额外开销。

1.5 实验设置

在 AffineQuant 中，稳定性因子 随着模型大小的增加，量化位数的减小，组大小的增加，而减小。对于 OPT－6．7B 和较小的模型，设置 。随着模型大小的增加，对权重量化为 3－bit 或更多的配置使用 。对于其他配置，从集合 中选择 。然后，排除了 MLP 模块中两个线性层之间的仿射变换。这是因为在较大的尺寸中优化大变换矩阵很有挑战性。此外，激活函数的存在使得矩阵的等效变换无效。

1.6 实验结果

如图 4 和图 5 所示，AffineQuant 在各种量化配置的所有模型的取得了一致的性能改进，表明 AffineQuant 不依赖于特定的量化配置。值得注意的是，AffineQuant 所取得的改进特别是在低比特量化或更小的模型尺寸的情况下。具体来说，在 OPT-125M 模型的 w3a16g128 配置中，AffineQuant 实现了 5.10 的困惑度降低，大大超过了OmniQuant 的性能。此外，在 w4a4 量化配置下，AffineQuant 在 C4 和 WikiText2 数据集的 LLaMA2-7B 模型上实现了 2.26 和 1.57 的困惑度降低。这些结果强调了在更有挑战性量化任务中扩展等价变换的优化空间的重要性。

在图 6 中，作者调整了式 6 中的稳定性因子 。 接近于 0 时，仿射变换理论上收敛到尺度变换。可以观察到，随着 的降低，OPT－125M 和 LLaMA－7B 的模型性能收敛到 OmniQuant。然而，在 LLAMA－7B 的情况下，较大的稳定性因子并不能保证变换矩阵的严格对角支配，导致训练崩溃。因此，有必要在保证 Levy－Desplanques 定理有效性的同时增加 。

参考

1. Awq: Activation-aware weight quantization for llm compression and acceleration
2. OmniQuant: Omnidirectionally Calibrated Quantization for Large Language Models
3. RPTQ: Reorder-based Post-training Quantization for Large Language Models
4. An extension of the Levy-Desplanque theorem and some stability conditions for matrices with uncertain entries