ICLR’25｜MambaQuant：首个Mamba系列模型量化方案，精度近乎无损还适用于标准LLM！

宣传一下我们被人工智能顶会ICLR-2025录用的文章，MambaQuant：

• https://arxiv.org/abs/2501.13484
• 后摩智能、哈尔滨工业大学、南京大学、东南大学

值得一提的是，该工作对transformer-based LLM模型的量化也有很大提升，例如在Llama2 7B模型上超过了Quarot，是个很通用的方法！

Abstract

Mamba是一种高效的序列模型，可与Transformer相媲美，在各类任务中展现出作为基础架构的巨大潜力。量化技术常用于神经网络，以减小模型大小并降低计算延迟。然而，将量化应用于Mamba的研究尚少，现有的量化方法虽然在CNN和Transformer模型中效果显著，但对Mamba模型却不太适用（例如，即使在W8A8配置下，QuaRot在Vim-T模型上的准确率仍下降了21%）。我们率先对这一问题展开探索，并识别出几个关键挑战。首先，在门投影、输出投影和矩阵乘法中存在大量异常值。其次，Mamba独特的并行扫描操作进一步放大了这些异常值，导致数据分布不均衡且呈现长尾现象。第三，即使应用了Hadamard变换，权重和激活值在通道间的方差仍然不一致。为此，我们提出了MambaQuant，这是一种训练后量化（PTQ）框架，包含：1）基于Karhunen-Loève变换（KLT）的增强旋转，使旋转矩阵能适应不同的通道分布；2）平滑融合旋转，用于均衡通道方差，并可将额外参数合并到模型权重中。实验表明，MambaQuant能够将权重和激活值量化为8位，且基于Mamba的视觉和语言任务的准确率损失均小于1%。据我们所知，MambaQuant是首个针对Mamba系列模型的综合性PTQ设计，为其进一步的应用发展奠定了基础。

Introduction

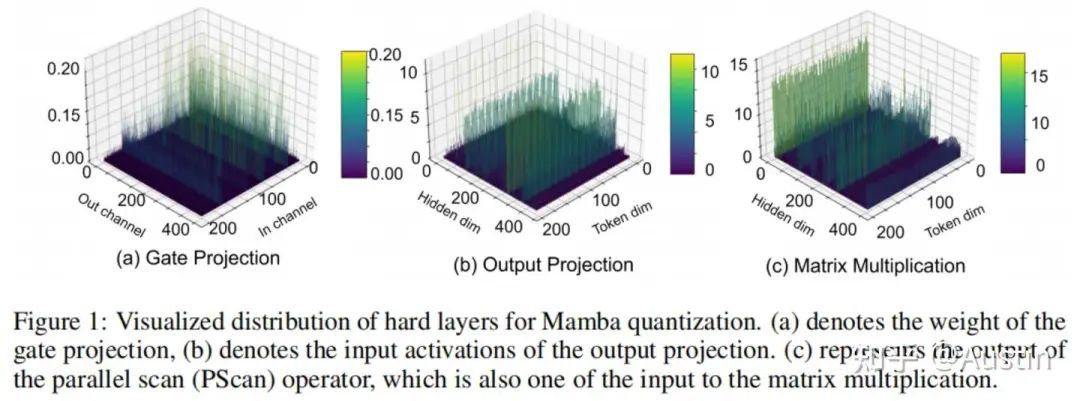
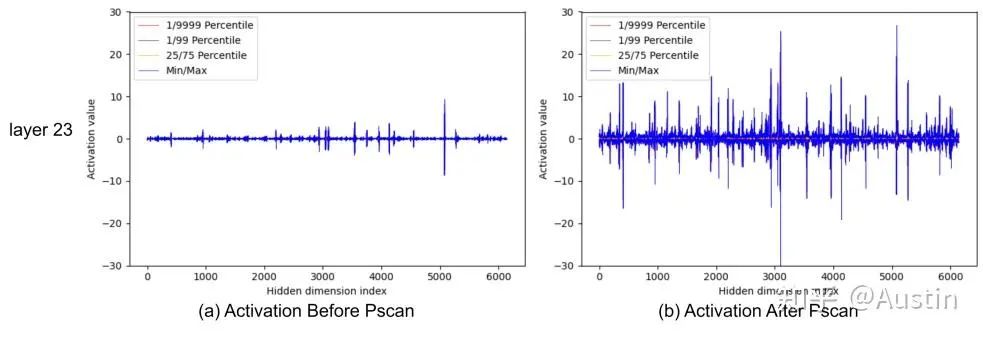
为了建立一套针对Mamba模型的综合量化方法，我们首先研究其中涉及的潜在限制和挑战：❶Mamba模型的权重和激活值中都存在显著的异常值。我们观察到，线性层的权重中存在异常值，尤其是在用于语言任务的 Mamba-LLM 的门投影层（图1a）中。我们还发现，线性层的某些输入在通道维度上表现出显著的方差。这种情况在用于视觉任务的 Vim 的输出投影层（图1b）中尤为明显。❷并行扫描（PScan）进一步放大了激活值的异常值。为了在每个时间戳获得隐藏状态，PScan算子（Smith等人，2022）会对一个固定的参数矩阵不断进行自乘运算。在这种情况下，值较高的通道会被放大，而值相对较低的通道则会被削弱。这种通道间明显的数值差异会直接扩展到激活值上（例如，如图1（c）所示的矩阵乘法的输入变量，以及图2所示）。

最近，基于 Hadamard 的方法因其能够使最大值均匀化以及具有等价变换特性，在 Transformer-based LLMs (T-LLMs) 的量化中取得了显著成功。例如，使用 QuaRot 将 LLAMA2-70B 量化为 4 位时，能保持 99% 的零样本性能。然而，将这种方法直接应用于 Mamba 模型会导致准确率大幅下降（例如，即使在 8 位量化的情况下，在 Vim上平均准确率仍然下降超过 12%）。为了解决上述问题，我们发表了MambaQuant这篇文章，（据我们所知）这是首个在Mamba系列模型上实现了高准确率W8A8/W4A8量化的工作，主要贡献包括：

1. 在离线模式下，我们提出基于 Karhunen – Loève 变换（KLT）的增强旋转。此技术将 Hadamard 矩阵与 KLT 矩阵相乘，使旋转矩阵能够适应不同的通道分布。
2. 在在线模式下，我们引入平滑融合旋转。这种方法在 Hadamard 变换之前进行平滑处理。额外的平滑参数被灵活地整合到 Mamba 模块的权重中，以避免额外的内存空间和推理步骤成本。

因此，量化数据的最大值和方差在通道维度上都得到了充分对齐，方法效果如图3所示

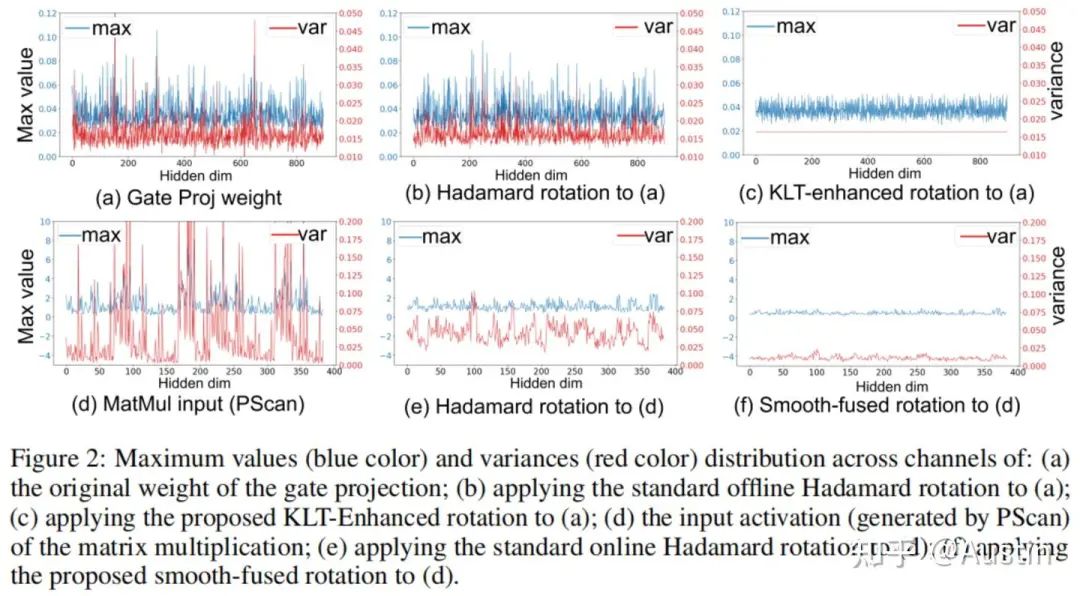
实验表明，MambaQuant 能够高效地将权重和激活值量化为8位，且在基于Mamba的视觉和语言任务上，准确率损失均小于1%。

Method

对Hadamard旋转效果不佳的分析

我们发现，该方法无法对齐量化变量的通道方差，从而忽略了不同通道之间的分布一致性。详细来说，给定一个中心化的数据矩阵（矩阵的列均值为零）X（权重或激活值），其维度为(n, m)，以及维度为(m, m)的Hadamard变换矩阵H，变换后的矩阵XH的协方差矩阵可以表示为：

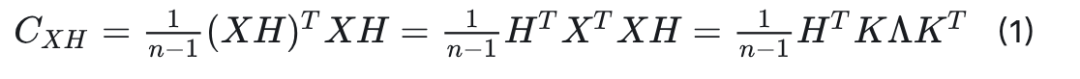
协方差矩阵的第l个对角元素可以表示为：

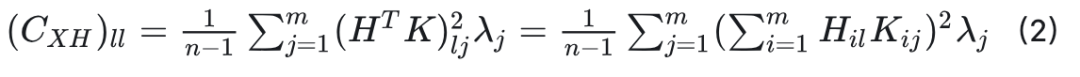
对于给定的 值，公式（2）表示第 个通道的方差。由于向量 随 变化，在大多数情况下无法证明通道方差在数值上接近。 此外，考虑到 H 是一个固定矩阵，而 和 都取决于输入，在所有情况下，Hadamard变换都不可能统一调整通道方差。Hadamard变换的这一特性不可避免地为每个通道形成了不同的分布，从而导致次优的量化效果。

KLT增强旋转

为了克服上述限制，我们引入了KLT来均衡通道方差。KLT识别数据中的主成分，并将数据投影到这些成分上，通过关注方差最大的方向来保留每个通道的最关键信息。在实际应用中，Mamba权重和激活值的均值通常接近于零，满足KLT的适用条件。具体而言，我们对由校准数据得到的中心化矩阵X的协方差矩阵进行特征值分解来应用KLT：

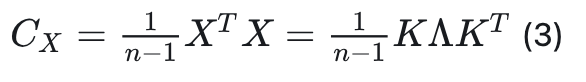
接下来，如公式(4)所示，通过将KLT应用于Hadamard矩阵H，可以得到KLT增强旋转矩阵

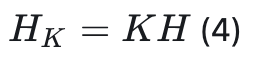
在公式(4)基础上，公式(1)可因此转化为公式(5)：

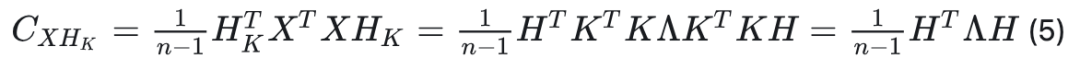
而公式(2)可变为公式(6)：

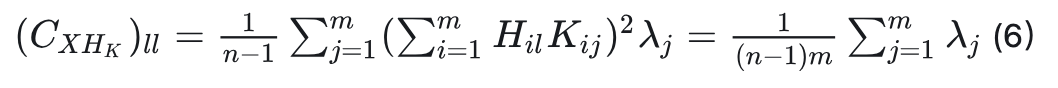
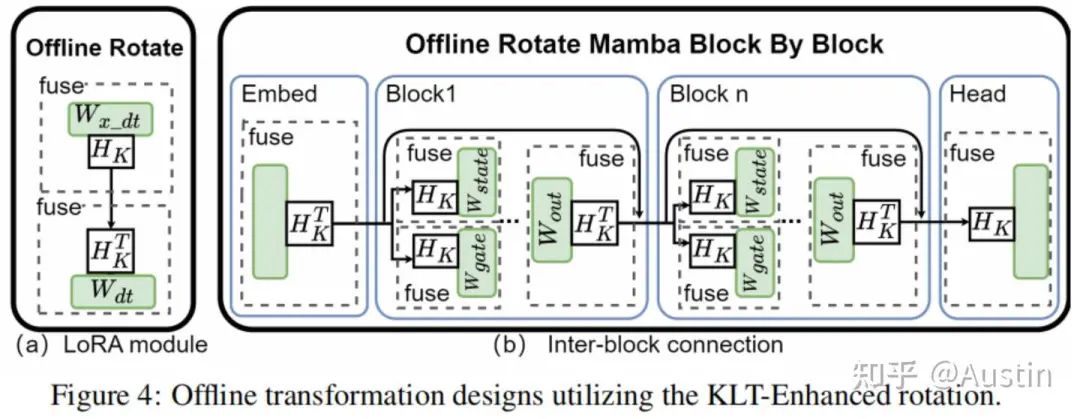
这样，每个通道的方差变得相同，使得量化变得容易得多。这种变换具有双重目的：它不仅均衡了不同通道之间的方差，还体现了KLT矩阵与Hadamard矩阵的独特属性，后者能够平衡最大值。在实践中，KLT是离线执行的，以避免额外的计算成本。为了将这种KLT增强的旋转矩阵应用于Mamba结构，我们修改了QuaRot中的离线变换。如图5所示，我们将此策略应用于LoRA模块和层间连接（其中输出投影、门投影和状态投影被变换）。

Smooth对齐旋转

为了在在线旋转中实现通道方差对齐，我们在执行在线Hadamard旋转之前引入了平滑(smooth)技术。采用这种方法的动机是通过一个平滑向量来使通道方差均匀化。通常，平滑因子可以被吸收到量化层的相邻层中例如SmoothQuant, OmniQuant。这种操作有效地避免了因引入额外参数而产生的额外内存分配和计算开销需求。然而，这种方法在Mamba模块中并不完全适用，这是由于非逐元素的SiLU操作以及PScan的复杂循环结构。为此，我们分别针对输出投影和矩阵乘法提出了两种不同的设计。

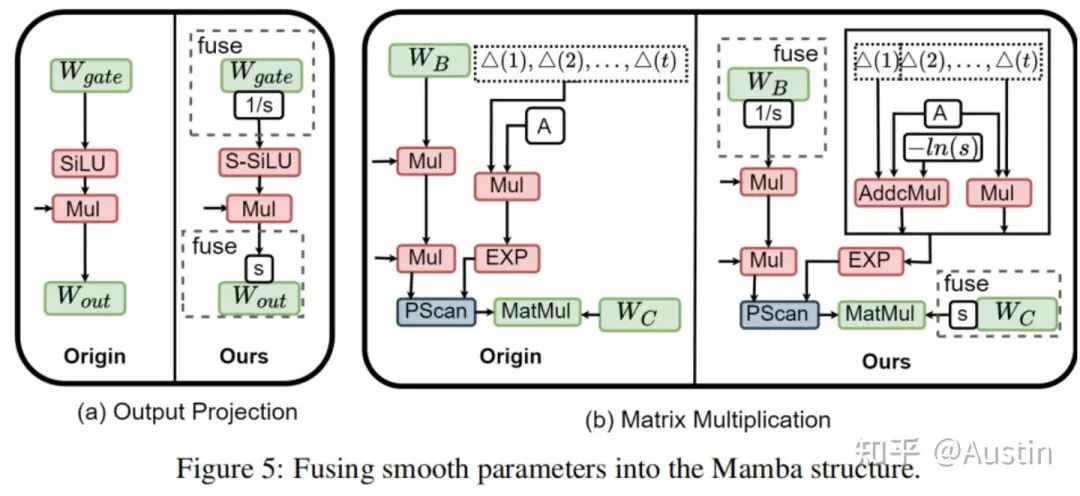
对于输出投影层： 我们提出S – SiLU，改进了传统的SiLU激活函数，以满足平滑融合量化的需求：

如图6(a)所示，S – SiLU函数在门投影上的应用可以表示为如下公式：

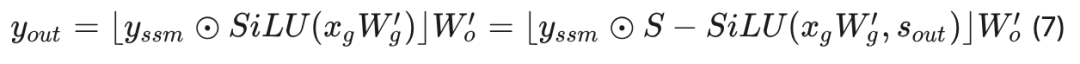
对于矩阵乘法层：如图6(b)所示，平滑参数s可以被自然的吸收到权重B和权重C中，然而A矩阵会在推理时执行多次的自乘运算，因此我们引入了计算友好的addcmul算子，仅对第一个时间步的A矩阵的运算做s参数的吸收融合，如公式(8)所示：

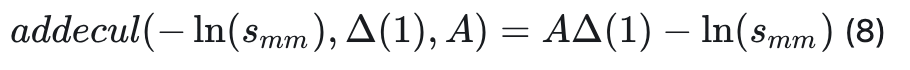
经过平滑处理后，输出投影和矩阵乘法的激活值的通道方差变得相对均匀。随后，我们针对Mamba结构修改并应用了在线Hadamard旋转，如图7所示。Hadamard矩阵H被动态地应用于输出投影和矩阵乘法的输入激活值，而转置后的H^T可以被吸收到相应的权重中。

Experiments

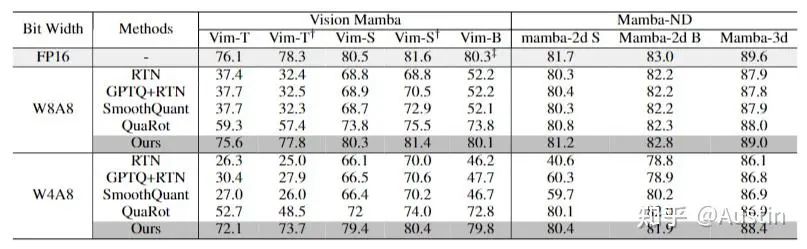
实验结果表明，MambaQuant 在 Mamba 系列模型上都取得了惊人的效果，表现超过Quarot，并远超其他的量化方案。例如其W8A8的精度在多种视觉语言的评估任务上都表现出小于1%的精度损失，其W4A8的量化也是实现了SOTA的效果。

值得一提的是，我们的通道方差对齐方法对精度有很明显的提升，该提升的可视化效果也十分显著。

这项工作首次在Mamba模型上实现了高精度量化，为Mamba模型的高效部署和推理开辟了新的途径，尤其是边缘设备上。同时该工作对transformer-based LLM模型的量化也有很大提升，值得进一步探索！

算法：社招、校招、实习生招聘

联系方式和地点

dawei.yang@houmo.ai 13813371526（微信同号）

️ 北京/南京/上海

研究方向（Mentor提供论文指导）

• 大模型及多模态算法研究（LLM、MLLM、VLLM等）
• 模型加速优化研究（PTQ、QAT、混合精度量化、模型压缩等）
• 软硬件协同设计（AI模型加速、算子硬件化、指令集开发等）

开发方向（Mentor提供工程指导）

• AI工具链开发（模型解析、图优化等）
• AI算子设计和开发（如投影变换、超越函数、LayerNorm、Grid-sample等）
• 模型部署优化（性能优化、Benchmark验证等）

部分研究成果

• Pushing the Limits of BFP on Narrow Precision LLM Inference. AAAI-2025
• MambaQuant: QUANTIZING THE MAMBA FAMILY WITH VARIANCE ALIGNED ROTATION METHODS. ICLR-2025
• OSTQuant: REFINING LARGE LANGUAGE MODEL QUANTIZATION WITH ORTHOGONAL AND SCALING TRANSFORMATIONS FOR BETTER DISTRIBUTION FITTING. ICLR-2025
• A 22nm 64kb Lightning-like Hybrid Computing-in-Memory Macro with Compressor-based Adder-tree and Analog-storage Quantizer for Transformer and CNNs. ISSCC 2024
• MIM4DD: Mutual Information Maximization for Dataset Distillation, NeuIPS 2023.
• RPTQ: Reorder-based Post-training Quantization for Large Language Models. arXiv preprint 2023.
• Post-training Quantization on Diffusion Models. CVPR 2023
• PD-Quant: Post-Training Quantization based on Prediction Difference Metric. CVPR 2023.
• Latency-aware Spatial-wise Dynamic Networks, NeurIPS 2022.
• Flatfish: a Reinforcement Learning Approach for Application-Aware Address Mapping. IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems (TCAD), 2022.
• PTQ4ViT: Post-Training Quantization Framework for Vision Transformers. European Conference on Computer Vision (ECCV), 2022.
• 3DPEE: 3D Point Positional Encoding for Multi-Camera 3D Object Detection Transformers. ICCV 2023.
• Stabilized activation scale estimation for precise Post-Training Quantization. Neurocomputing 2023.