
结论写在前面(太长不看版)

论文标题:
HiAR-ICL: High-level Automated Reasoning Paradigm in In-Context Learning via MCTS
https://arxiv.org/pdf/2411.18478
https://jinyangwu.github.io/hiar-icl/
https://huggingface.co/papers/2411.18478

引言
为了克服这些限制,论文提出了 HiAR-ICL,一种结合蒙特卡洛树搜索(MCTS)的高级自动推理方法。HiAR-ICL 将关注点从具体示例转向抽象的思维模式,扩展了上下文学习的内涵,推动了推理能力的进一步发展。

研究动机

受到这些研究的启发,论文采用了 MCTS 结构来探索更全面的推理路径,同时将已知的认知模式引入到 ICL 中,极大地减少了搜索空间的计算复杂度,同时保持了高效的推理性能。因此,论文提出的 HiAR-ICL 方法,充分平衡了推理效率和准确性。

HiAR-ICL方法概述

▲ 图2:方法图
此外,文章还设计了一个认知复杂度框架,能够动态匹配问题与适当的思维卡片。具体包含以下四步:
Step 1: Define Atom Reasoning Actions(原子推理动作的定义)
这些动作的设计旨在模拟人类的高阶认知行为,使得模型能够更有效地进行问题分解、逻辑推理和自我修正。
Step 2: Construct Thought Cards via MCTS(通过MCTS构建思维卡片)
通过这种方式,HiAR-ICL 能够在没有外部监督的情况下,自适应地生成和优化推理路径,提高了模型的泛化能力和推理效率。
Step 3: Select Reasoning Patterns(推理模式选择)
HiAR-ICL 引入了一个认知复杂度框架,包括子问题数量、问题条件复杂度和语义相似度三个指标。基于这个框架,HiAR-ICL 能够动态匹配问题与适当的思维卡片,选择最适合目标问题认知复杂度的思维卡片作为推理模板。
Step 4: Solve and Verify(推理和验证)
实际上,上述推理过程也可以看作是高度优化的树搜索。通过引入先验信息–即推理模式,模型能够迅速定位树搜索结构中每一层的节点,迅速向下找到较优路径。因此,HiAR-ICL 在保证潜在答案空间基本不变的情况下,极大压缩了探索时间,提升了计算效率,实现了性能和效率的双重保证。

实验结果分析
HiAR-ICL 的实验结果分析显示了该方法在多个复杂推理基准上的有效性和优越性能。以下是实验结果的几个关键点:
4.1 性能提升
HiAR-ICL 在多个推理基准上取得了显著的性能提升,显著超过了现有 CoT 等方法,且针对小模型的提升效果明显。例如,Llama3-8B-Instruct 在 MATH 基准上的准确率从 17.8%(few-shot CoT)提高到使用 HiAR-ICL 的 43.2%,Qwen2-7B-Instruct 从 52.9% 提高到 63.8%,Yi-1.5-6B-Chat 从 40.5% 提高到 54.0%。

4.2 与顶尖闭源LLMs的比较
HiAR-ICL 赋能的 LLMs 在性能上与拥有数千亿参数的顶尖闭源模型相媲美,甚至在某些情况下超过了这些闭源模型。特别是 Qwen2.5-7B-Instruct 模型,在 MATH 基准测试中的表现超过了 GPT-4o。
![]() ▲ 表2:HiAR-ICL和闭源模型的对比
▲ 表2:HiAR-ICL和闭源模型的对比
4.3 与树搜索方法的比较
与其他树基推理方法相比,HiAR-ICL 在 GSM8K 和 MATH 数据集上展现出了优越的性能和显著的泛化能力。
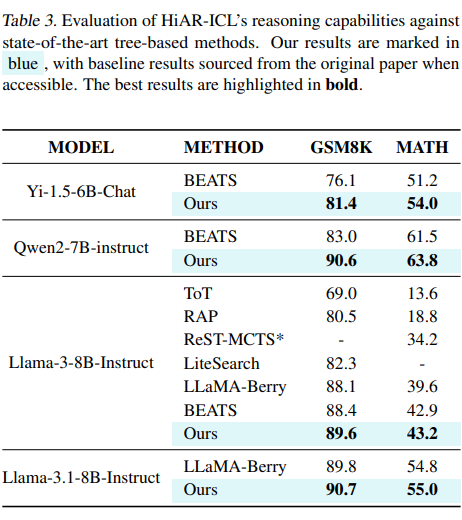 ▲ 表3 HiAR-ICL和最新树搜索方法对比
▲ 表3 HiAR-ICL和最新树搜索方法对比
4.4 计算效率
作者还和目前的 SOTA 方法 rStar 进行了对比,发现整体性能保证的同时,极大降低了时间复杂度。

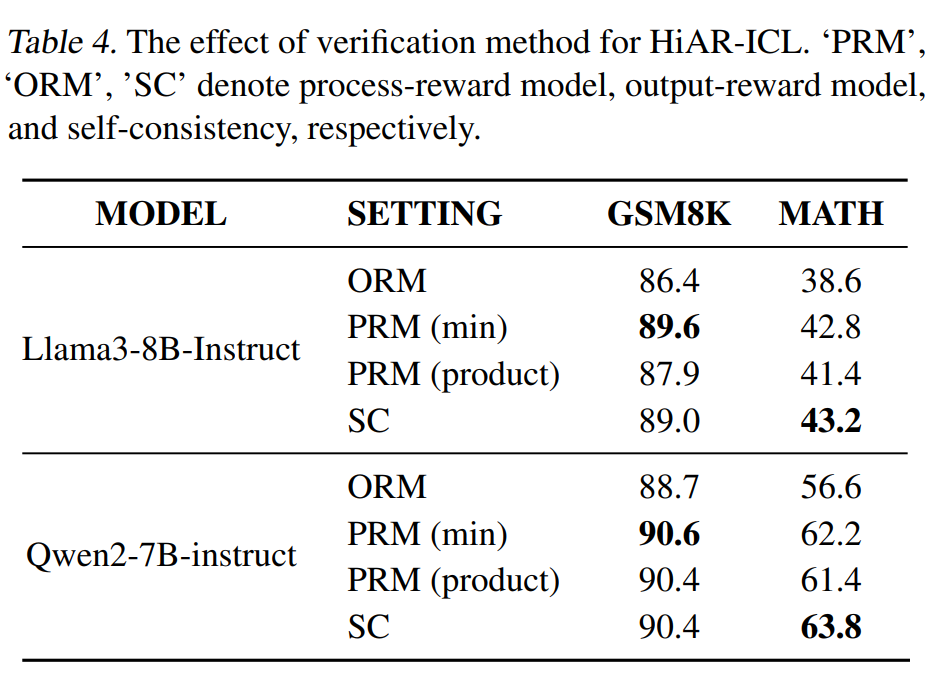
4.5 不同验证方法的效果
在验证部分,HiAR-ICL 采用了过程奖励模型(PRM)、输出奖励模型(ORM)和自我一致性(SC)三种方法。实验结果显示,即使是简单的一致性基础方法也能有效地选择最精确的推理链,展现出强大的性能。这也展示了这个方法的有效性,可能通过更加精细设计的验证方法,能够实现更好的性能。

总结
(文:PaperWeekly)
