
极市导读
关于强化学习中PPO算法的全面解读,从基础概念到算法细节,旨在帮助读者深入理解PPO的理论基础和实现机制。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
在去年的这个时候,我以deepspeed-chat的代码为例,解读了rlhf运作的流程。当时写这篇文章的目的,主要是想让读者在没有强化学习知识的情况下,能从直觉上快速理解这份代码,以便上手训练和修改。
由于这篇文章侧重“直觉”上的解读,因此有很多描述不严谨的地方。所以去年我就想接着敲一篇比较严谨的介绍强化学习理论的文章(策略梯度->actor-critic -> PPO),但是由于敲公式真得太累了,所以一直delay到今天。
所以今天这篇文章就来做这件事,我的主要参考资料是Sutton的这本强化学习导论(http://incompleteideas.net/book/the-book-2nd.html)。在现有的很多教材中,一般会按照这本导论的介绍方式,从MDP(马尔可夫决策过程)和价值函数定义介绍起,然后按照value-based,polciy-based,actor-critic的顺序介绍。但是由于本文的重点是actor-critic,所以我在写文章时,按照自己的思考方式重新做了整理:
-
我们会先介绍policy-based下的优化目标。 -
然后再介绍价值函数的相关定义。 -
引入actor-critic,讨论在policy-based的优化目标中,对“价值”相关的部分如何做优化。 -
基于actor-critic的知识介绍PPO。
为什么在网络上已经有无数强化学习理论知识教程的前提下,我还要再写一篇这样类型的文章呢?主要是因为:
-
作为一个非RL方向出身的人,我对RL的理论知识其实一直停留在“它长得是什么样”,而不是“它为什么长这样”
-
当我想去探究“它为什么长这样”的时候,我发现最大的难点在各类资料对RL公式符号定义的太混乱,或者写的太简略了。举例来说:
-
我们在RL会看到大量 这样求期望的形式, 但是很多公式会把E的下标省略掉, 使人搞不清楚它究竟是从哪里采样,而这点非常重要。 -
在RL的公式中, 混合着随机变量和确定性变量, 对于随机变量我们常讨论的是它的期望。可是在有些资料中, 经常给出诸如 这样的形式, 且不带符号说明。乍一看你很难想到, 它究竟代表某一次采样中的即时奖励, 还是代表多次采样的即时奖励的期望? 诸如此类 -
最后,只有当我把所有的过程按自己的思路想一遍,推一遍后,我才发现原来之前自己还有这么多理解不深刻的地方。写这篇文章的过程,也是在问自己为什么的过程。
【全文目录如下】
一、策略
二、奖励
三、运动轨迹和状态转移
四、Policy-based下的强化学习优化目标
五、策略的梯度
5.1基本推导
5.2总结
六、价值函数
6.1 总述:衡量价值的不同方式
6.2 回报
6.3 状态价值函数
6.4 动作价值函数
6.5 状态价值函数和动作价值函数的关系
6.6 优势函数和TD error
七、Actor-Critic
7.1 Actor优化目标
7.2 Critic优化目标
7.3 Actor和Critic之间的关系
八、PPO
8.1 朴素Actor-Critic存在的问题
8.2 重要性采样
8.3 GAE:平衡优势函数的方差与偏差
8.4 PPO前身:TRPO
8.5 PPO做法1: PPO-Clip
8.6 PPO做法2: PPO-Penalty
8.7 PPO中的critic loss
一、策略(policy)
策略分成两种:确定性策略和随机性策略。我们用表示策略的参数。
1.1 确定性策略
智能体在看到状态 的情况下, 确定地执行
1.2 随机性策略
智能体在看到状态 的情况下, 其可能执行的动作服从概率分布 。也就是此时智能体是以一定概率执行某个动作 。
在我们接下来的介绍中,都假设智能体采用的是随机性策略。
二、奖励(Reward)
奖励由当前状态、已经执行的行动和下一步的状态共同决定。
2.1 单步奖励
-
奖励和策略 无关 -
用于评估当前动作的好坏,指导智能体的动作选择。
2.2 T步累积奖励
T步累积奖励等于一条运动轨迹/一个回合/一个rollout后的单步奖励的累加.
2.3 折扣奖励
这里 。
三、运动轨迹(trajectory)和状态转移
智能体和环境做一系列/一回合交互后得到的state、action和reward的序列,所以运动轨迹也被称为episodes或者rollouts, 这里我们假设智能体和环境交互了 次:
-
是初始时智能体所处的状态, 它只和环境有关。我们假设一个环境中的状态服从分布 , 则有 . -
当智能体在某个 下采取某个动作 时, 它转移到某个状态 可以是确定的, 也可以是随机的: -
确定的状态转移: ,表示的含义是当智能体在某个 下采取某个动作 时,环境的状态一定会转移到 -
随机的状态转移:
在我们接下来的介绍中,都假设环境采用的是随机状态转移。
四、Policy-based强化学习优化目标
抽象来说,强化学习的优化过程可以总结为:
-
价值评估:给定一个策略 , 如何准确评估当前策略的价值 ? -
策略迭代:给定一个当前策略的价值评估 , 如何据此优化策略 ?
整个优化过程由以上两点交替进行, 最终收玫, 得到我们想要的最优策略 和能准确评估它的价值函数

此时, 你肯定会想, 这是否意味着强化学习过程中一定存在 和 两个实体呢? 例如, 这是否意味我们一定要训练两个神经网络,分别表示策略和价值评估?答案是否定的:
-
你可以只有一个价值实体 , 因为它的输入和状态与动作相关(这里我们不区分 V 和 Q , 留到后文细说)。这意味着只要我们知道状态空间 和动作空间 就可以作用到这两个空间上帮助我们衡量哪个状态/动作的价值最大,进而隐式地承担起制定策略的角色,我们也管这种方法叫value-based。 -
你可以只有一个策略实体 , 在对策略的价值评估中, 我们可以让策略和环境交互多次, 采样足够多的轨迹数据,用这些数据去对策略的价值做评估,然后再据此决定策略的迭代方向,我们也管这种方法叫 policy-based。 -
你可以同时有价值实体 和策略实体 , 然后按照上面说的过程进行迭代, 我们也管这种方法叫 actorcritic, 其中actor表示策略, critic表示价值。这是我们本文讨论的重点。
接下来,我们就直接来看policy-based下的强化学习优化目标:
我们来详细解读这个目标:
-
:表示一条轨迹序列。 -
:智能体所采取的策略,下标 表示和策略相关的参数。 -
:表示这条轨迹序列的累积奖励。 -
:在使用策略 的情况下, 产出某条轨迹的概率 -
: 我们知道, 当前这条轨迹序列是在使用策略 的情况下采样出来的, 所以 隐藏的完整含义为:
-
-
基于策略的强化学习的总目标是,找到一个策略 ,使得它产出的轨迹的【回报期望】尽量高。 报期望表示为 。 -
为什么这里我们讨论的是【回报期望】,而不是某一个具体的回报值?这是因为策略和状态转移具有随机性,也就是对于一个固定的策略,你让它和环境交互若干次,它每次获得的轨迹序列也是不一样的,所以是个随机变量,因此我们讨论的是它的期望。从更通俗的角度来讲,你评价一个策略是否好,肯定不会只对它采样一次轨迹,你肯定需要在足够多次采样的基础上再来评估这个策略。
五、策略的梯度上升
5.1 基本推导
现在我们知道强化学习的总优化目标是:

我们据此来计算梯度:

其中,第2行~第3行是因为:

我们对一项再进行展开推导。我们知道策略和状态转移都是随机的,同时我们设一条轨迹有个timestep,则我们有:
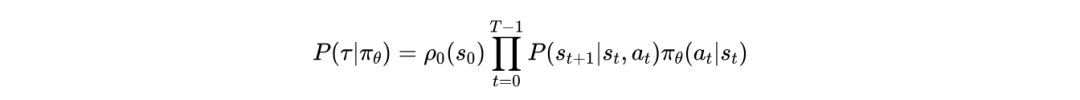
据此我们继续推出:

被约去的两项是因为这里我们是在对策略求梯度,而这两项和环境相关,不和策略相关。
综上,最终策略的梯度表达式为:
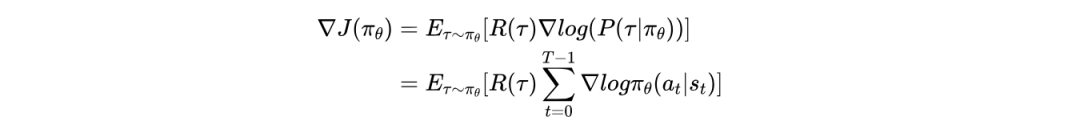
5.2 总结
在基于策略的强化学习中,我们期望max以下优化目标:
基于这个优化目标,策略的梯度为:
这个梯度表达式有一个简单的直观理解: 当 越高时,动作 贡献的梯度应该越多,这是因为此时我们认为 是一个好动作,因此我们应该提升 ,即提升在 下执行 的概率。反之亦然。
在实践中,我们可以通过采样足够多的轨迹来估计这个期望。 假设采样 N 条轨迹, N 足够大,每条轨迹涵盖 步, 则上述优化目标可以再次被写成:

对应的梯度可以被写成:

六、价值函数(Value Function)
通过上面的推导,我们知道在强化学习中,策略的梯度可以表示成

这里 表示一整条轨迹的累积奖励或者累积折扣奖励。
当你端详这个公式时, 你可能会有这样的疑问: 是整条轨迹的奖励, 但是 却是针对单步的。我用整条轨迹的回报去评估单步的价值,然后决定要提升/降低对应 的概率,是不是不太合理呢?例如:
-
一条轨迹最终的回报很高,并不能代表这条轨迹中的每一个动作都是好的。 -
但我们又不能完全忽视轨迹的最终回报,因为我们的最终目标是让这个回合的结果是最优的。 -
综上,在衡量单步价值时,我们最好能在【单步回报】和【轨迹整体回报】间找到一种平衡方式。
有了以上这些直觉, 你开始考虑用一个更一般的符号 来表示各种可行的价值函数, 你用 替换掉了上面的 , 这下策略的梯度就变成:
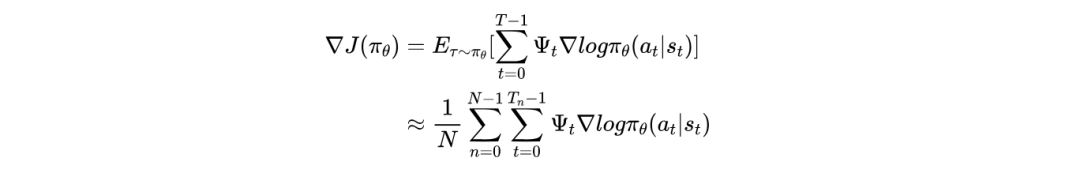
6.1 总述:衡量价值的不同方式
总结来说可能有如下的实现方式:

我们来做逐一讲解。
(1)整条轨迹累积奖励/累积折扣奖励
这就是我们前文一直沿用的方法,即:
你可以通俗理解成 (省略了折扣因子)
(2)t时刻后的累积奖励/累积折扣奖励
由于MDP的假设,t时刻前发生的事情和t时刻没有关系,t时刻后发生的事情才会受到t时刻的影响,所以我们可以令:
(3)引入基线
我们沿着(2)继续看, 假设在单次采样生成的估计中, t 时刻后的累积奖励为 , 如果这个值很高,那一定证明在某个 下采取某个 一定好吗?答案是否定的,因为这里的”高”是一个绝对概念,而我们更想知道的是一个相对概念:这个动作究竟比别的动作好多少?同时,由于采样具有随机性,有些动作只是没被采样到, 并不代表它们不好。所以这里我们引入一个基线(baseline)的方法来做调控:
这里基线的实现方式也可以有多种,比如当我们采样了一堆轨迹,我们可以找到这些轨迹中状态为 的数据, 求这些数据在(2)下的奖励并做平均(也就是求了个期望)当作基线。
(4)动作价值函数
(5)优势函数
(6)状态价值的TD error
以上三点间具有某种联系,我们这就来详细展开讲解它们。我们先关注这三者,然后再来关注TD error。
我们沿着(4)~(6)继续来讨论的可行形式,一种符合直觉的处理方法是:
-
智能体来到了某个状态 下, 它的动作空间是 。智能体的策略 本质上是一种概率分布。它按 的概率决定要sample出哪个 。 -
而在”采样->训练->更新策略参数”的这个循环过程中,智能体要做的事情就是,如果在某个状态 下,某个动作 带来的回报”大”,那么智能体就应该提升 这个概率,也就是智能体据此不断调整 的分布。 -
那么怎么衡量在某个 下,执行某个 带来的回报是否”大”? 我们可以去计算【执行 带来的回报 – 执行其它动作的回报】,这个差值可以告诉我们 比别的动作要好多少。
那么什么叫【执行 带来的回报】和【执行其它动作带来的回报】?
-
假设你在玩马里奥游戏,你来到了画面的某一帧(某个 ) -
你在这一帧下有3个选择:顶金币,踩乌龟,跳过乌龟。你现在想知道执行“顶金币”的动作比别的动作好多少。 -
你先执行了”顶金币”的动作(即现在你采取了某个确定的 pair), 在束。在每一回合中, 你都记录下从(这一帧,顶金币)出发,一直到回合结束的累积奖励。你将这若干轮回合的奖励求平均,就计算出从 (这一帧, 顶金币) 出发后的累积奖励期望, 我们记其为 。 -
现在你重新回到这一帧(你回到了一个确定的 上),对于”顶金币”,”踩乌龟”,”跳过乌龟”这三个动作,你按照当前的策略 从这三者中采样动作(注意,我们没有排除掉”顶金币”),并继续玩这个游戏直到回合结束,你记录下从 出发一直到回合结束的累积回报。重复上面这个过程若干次,然后你将这若干轮回合的奖励求平均, 就计算出从(这一帧)出发后的累积奖励期望, 我们记其为 。 -
你会发现不管是Q还是V,下标都有一个,这是因为它们和你当前采取的策略是相关的 -
从直觉上, 我们取 这个差值, 就可以衡量在某个状态 下, 执行某个动作 , 要比其它的动作好多少了。这个差值, 我们可以理解为”优势”(advantage),这个优势更合理地帮助我们衡量了单步的奖励, 所以我们可以用它替换掉上面的 。 -
当优势越大时,说明一个动作比其它动作更好,所以这时候我们要提升这个动作的概率。
通过上面的例子,我们已经引出一些关于价值函数的基本概念了:
-
:状态价值函数 -
:动作价值函数 -
:优势
所以接下来,我们就从理论的角度,详细展开介绍它们。
6.2 回报
在前面的例子中, 我们说过, 当我们从 某一帧, 顶金币 出发后, 我们玩游戏一直到回合结束,然后我们执行 , 作为这个回合的累积奖励。
但其实,我们计算这个累积奖励的目的是衡量从 某一帧, 顶金币)这一【单步】出发后带来的未来收益。而对于这一个【单步】来说,一般离它越近的timestep受到它的影响越大,离它越远的timestep受到它的影响越小。在这个直觉的启发下, 我们采用【累积折扣奖励】来定义单步(也就是某个t时刻)的回报:
在接下来的讲解中,提到某一个回合中【单步】的奖励,我们说的都是【累积折扣奖励】
6.3 状态价值函数(State-Value Function)
状态价值函数的原子定义如下:
我们先来解释相关的符号:
-
首先, 状态价值函数一定是和策略相关的。相同的状态 下(例如”同一帧游戏画面”),不同的策略 产生的结果也不一样(例如不同的人玩这个游戏)。所以我们带上了下标 。 -
其次, 不是随机变量, 而是一个确定值。这是因为此时我们衡量的就是从某个确定的状态 出发带来的累积奖励期望。 -
但是, 却是一个随机变量, 这是因为因为我们的策略 和环境转移 都是随机的。所以尽管每次智能体都从 出发,但采样到的轨迹却不一样。所以这里我们谈的是 的期望。
上面是状态价值函数最原子的定义,我们把这个定义展开,以便更好理解 是如何计算的(这里我直接对我笔记截图了,因为latex公式显示不出来):

上面这个展开细节帮助我们从理论上理解上面举的例子:从马里奥游戏的某一帧 出发,如何求这一帧的累积回报期望,也就是求这一帧下所有动作的累积回报期望。我们从第 4 行推导开始讲起:
-
第4~第5行,即如何从 推到 ,可以参见蘑菇书EasyRL的2.2.2的第1节 https://datawhalechina.github.io/easy-rl/#/chapter2/chapter2
-
第5~第6行讲述我们如何对期望E中的结果做展开。我们以 为例:
-
仅从这个表达式上看,它表示从某个状态 出发,在执行策略 的情况下, 的期望。我们前面说过,由于策略和状态转移具有随机性,因此 也是个随机变量。所以这里我们讨论的是【期望】而不是某个 值。 -
理解了这一点, 就不难理解第 6 行的关于策略和状态转移的两个求和展开项。你可以把这些求和项理解成从状态 出发, 做了无数次采样后的结果。 -
同时, 就是我们在之前定义的奖励函数, 它由三个入参决定。在我们把 展开成两个求和项后, 都是确定的值而不是随机变量了,所以这里 也是一个确定的值, 从 出发某次采样过程中得到的确定值 。 -
第6行后的推导过程都比较好理解,这里不再解释。
我们在学习 rl 的过程中, 会看到很多材料把上述公式写成 或者 之类的形式, 由于对缺少必要的下标, 这些简略的形式具有歧义性, 使人混淆。所以这边我们干脆多费一点力, 把所有的符号都展示出来, 更方便大家深入理解 的含义。这就是这里大费周章写出上述推导过程的意义。
6.4 动作价值函数(Action-Value Function)
同样,我们先来看动作价值函数的原子定义:
我们来解释相关符号:
-
首先,动作价值函数也是和策略相关的。从之前的例子我们知道,动作价值函数衡量的是从某个确定的出发后,例如从(马里奥游戏某一帧,顶金币)出发,一直到回合结束为止的累积奖励期望。在策略不一样的情况下(例如玩游戏的人不一样),即使大家都从某个确定的,最后的累积奖励期望也是不一样的。所以动作价值函数一定是对某个而言的。 -
其余要注意的地方和一致,这里不再赘述。

6.5 动作价值函数和状态价值函数的互相转换
我们来简单回顾下上面的内容。
状态价值函数的原子定义为:
动作价值函数的原子定义为:
展开状态价值函数的原子定义,我们得到:
展开动作价值函数的原子定义,我们得到:
根据这两者的原子定义展开式,我们得到两者的关系为:

关于V和Q,我们可能在脑海里一直有“V是Q的期望”这样一个模糊的印象,但是却很难做具象化的解读。希望这里通过上面马里奥游戏的例子 + 具体的推导过程,能帮助大家更深入了解V和Q的关系。
6.6 优势函数和TD error
在马里奥游戏的例子中, 我们曾经对优势做过简单的定义: 我们取 这个差值, 就可以衡量在某个状态 下, 执行某个动作 , 要比其它的动作好多少了, 这个差值就是优势。
我们展开来讲优势函数,在前面的推导中我们已知:
而对于,我们可以把它重新改写成:
之所以这样改写, 是因为 只依赖于这个确定的 , 而与 无关。
基于这两个式子,我们可以写成优势函数的表达式:

大家发现了吗:
-
假设这里的 等于那个客观世界存在的状态价值函数的真值, 那么TD_error就是优势函数的无偏估计。这意味着在期望的意义下,使用TD_error近似优势函数不会引起系统性的偏差。 -
假设这里的 不等于那个客观世界存在的状态价值函数的真值, 那么TD_error对于优势函数则是有偏的。 这意味着由于 的不准确,我们无法用 去近似那个真实的优势函数,因为我们将引入系统性偏差。(读到这里,你可能已经开始联想到在actor-critic算法下,用于估计 的 critic网络在没有收玫之前都是偏离真值的,这就意味着此时我们用TD-error去近似优势是有偏的,所以这时我们就要请GAE出场了, 这是后话, 我们放在后文细说)
七、Actor-Critic
我们先来回顾之前定义的policy-based下的策略梯度:

其中,衡量单步价值的可以有如下几种设计方案:

基于之前的分析,我们现在选择第6种(TD error)作为 ,它衡量在某个时刻 t 选择某个动作 a 会比选择其它的动作要好多少。 需要注意的是, 本质上当 等于客观存在的真值 时, 6 是 5 的无偏估计。
在actor-critic方法下,我们用神经网络 来表示策略(actor),神经网络 来表示价值(critic),所以这里我们进一步把 写成 。注意,这可能不是一个好写法,因为 V 一定是针对某个 而言的,anyway我们需要把这点记在心中, 在后文的表示中可能会出现 和 交替使用的场景, 他们都表示一个东西, 只是笔者写烸了可能忘记从一而终了…
接下来我们来看actor loss和critic loss的具体表达式。
7.1 Actor优化目标
现在我们可以把actor优化目标写成如下形式:

但是有时,一个回个中的timesteps可能非常多,我们无法等到回合结束再进行训练。既然我们已经使用了TD error来估计单步的优势,我们其实可以按照单步的方法进行更新(即你的batch_size是N,其中的每条数据都是一个单步数据),即actor优化目标可以写成:
在接下来的表示中,我们都将采用这种形式。对应的策略梯度前面写过很多遍了,这里就不写出来了。
7.2 Critic优化目标
同理,在单步更新下,我们可以把critic优化目标写成:
对应的critic梯度这里也略去。
7.3 Actor和Critic之间的关系
关于7.1节中,actor这个优化目标的改写我们已经很熟悉了,但对于7.2中的actor loss你可能还是满腹疑惑,例如:
-
看样子,actor loss是在让优势趋于0,但是如此一来,每个动作的好坏不就都差不多了?那你怎么能选出那个最好的动作呢?
为了解答这个问题,我们先回想第四节中提到的“价值评估->策略迭代”这样一个循环的过程:
-
价值评估: 给定一个策略 , 如何准确评估当前策略的价值 ? -
策略迭代: 给定一个当前策略的价值评估 , 如何据此优化策略

我们结合actor-critic的框架把这个循环的优化过程展开来讲:
-
我们从”策略迭代步骤开始”, 假设我们有一个策略 , 且同时有一个能准确评估它的价值的 。基于这个 , 我们计算某个 状态下动作 的优势 , 如果这个优势比较高, 那么我们就应该提升 这个概率。我们按照这个方式去改变策略的分布, 最终会得到一个新策略 。
-
那么, 什么时候这个 就是我们要找的最优策略 ? 我们假设当策略走到 时, 有一个客观存在的最优的动作 。那么如果当前这个策略走到 时,产出 的概率已经是1或者是最大的,那么就证明策略已经没有提升的空间了,当前的策略已到最优(注意,这里我们始终假设 是能准确估计一个策略的价值的)。
-
那么如果策略产出 的概率已经是1或者最大时, 优势会发生什么变化? 从6.5节中的推导里我们知道 ,由此不难得知,此时 会非常接近或者等于 ,也就是此时我们有 。
-
翻译成人话来说,就是当优势趋于 0 的时候,不是说所有的动作都区分不出好坏了。而是此时策略已经趋于最优,他本来产出最优的 的概率就是最大的。而不是像它还没优化好之前那样,还以相当的概率产出别的 们,所以我们要在这些 们之间去比较优势。
-
现在我们回答”价值评估”步骤上来:此时我们做完了策略迭代,使得 ,那么之前用于衡量 的 已经不适用了,我们需要找到一个 来正确衡量 。而当策略从 改进到 后,这个 等式右侧的分布也有所调整,所以我们应该让等式左侧去拟合等式的右侧, 这样才能得出一个可以正确评估 的
-
我们把以上内容换成比较好理解,但可能不太精确的人话:当我们推动critic loss(优势)趋于0时:
-
对于actor来说,是推动它找到某个状态下最佳的动作,逐步向****拟合 -
对critic来说,是推动它准确衡量当前策略的价值,逐步向****拟合
八、PPO
8.1 朴素Actor-Critic的问题
在理解critic loss为何如此设计的前提下,critic的梯度就比较好理解了,这里我们不做过多解释。我们把目光再次放回actor的梯度上来:

再次注意, 这里我们写成 的形式其实是不完整的, 它只是用来刻画 是 critic 网络的参数, 我们还必须铭记 衡量的是某个策略 的价值, 当这个策略发生迭代而变动时, 也会变动。
观察这个梯度表达式,我们会发现如下问题:
问题1:每次执行这个梯度更新时,我们都需要对进行若干次回合采样。我们知道智能体和环境交互的时间成本(fwd)比较高,也就是整个训练过程会比较慢
问题2: 我们在前面说过, 实际训练的过程中, 用 critic网络拟合出来 并不一定是能准确衡量 的那个价值函数, 所以这里我们用TD error去估计优势其实是有偏的。 为了降低这种偏差, 我们需要对 进行改造,改造的方法之一就是GAE。
接下来我们就详细来看如何解决这两个问题。
8.2 重要性采样
在朴素的方法中,我们使用和环境交互若干次,得到一批回合数据,然后我们用这个回合数据计算出来的奖励值去更新。我们管这个过程叫on-policy(产出数据的策略和用这批数据做更新的策略是同一个)
而现在,为了降低采样成本,我们想做下面这件事:
-
假设某次更新完毕后, 我们得到策略 -
我们用 和环境交互, 得到一批回合数据。 -
我们将把这一批回合数据重复使用 次: 即我们先把这批数据喂给 ,更新得到 ;我们再把这批数据喂给 , 更新得到 ;以此类推,做 k 次更新后,我们得到 。我们管这个过程叫off-policy(产出数据的策略和用这批数据做更新的策略不是同一个)。 -
在这k次更新后, 我们令 。重复上面的过程, 直到达到设定的停止条件为止。
我们从更理论的角度来看待这个off-policy的过程:
-
假设有两个分布 -
最开始我想从 中进行多次采样, 然后求函数 的期望。例如我想从 中进行采样, 然后求累积奖励的期望,这个期望我们表示成 -
但是现在, 因为某些原因, 我们无法从 中直接采样, 只能从另一个分布 中进行采样了, 那么此时我们要怎么表示 ? -
为了解决这个问题,我们做如下变换:

也就是说,当我们从不同于 的分布 上采样 x 时,从数学上我们确实有办法改写 , 简单来说就是加上一个权重 , 我们管上述的转换过程叫【重要性采样】。
虽然数学上是有办法改写了,但是实际操作中,我们可能遇到p(x)和q(x)分布差异较大的问题。这里我直接引用李宏毅老师的课堂ppt来说明这一点:

-
我们假设 的真值是负数。 -
由于p(x)和q(x)差异较大。在某次采样中,我们从q(x)里进行采样,大概率会采集到图中绿色曲线的高处,此时f(x)是正的。也就是说,在单次采样中,我们大概率会得到一个正的f(x)。 -
所以,只有经过尽可能多次的采样,让某次能命中q(x)这个绿色曲线的低处。这时p(x)/q(x)较大,也就赋予这个好不容易采样到的负的f(x)非常大的权重,这才足以抵消之前正f(x)的影响。 -
综上所述,当p(x)和q(x)差异较大时,我们需要通过足够多的采样来抵消这种差异对期望的最终影响。我们先记住这一点,在后面我们再来说这一点对我们策略的影响。
知道了重要性采样的过程,现在我们又可以根据它重写我们的优化目标了。
重要性采样前,策略的梯度是:
重要性采样后,策略的梯度是:
我们根据重要性采样构造了这个新的策略梯度,那么对应的新的actor优化目标就可以从这个策略梯度中反推出来:
特别注意 , 它意味着我们这一波的训练数据是由old策略采集来的。
但是到这步为止, 我们还要在心里铭记一个问题, 如何解决 和 分布差异过大的情况。我们先来看对优势函数的改进方法,然后再回来讲这个问题的解决办法。
8.3 GAE:平衡优势函数的方差和偏差
再回顾下6.6节的内容:在假设 能正确评估策略 的价值的前提下,我们用TD_error作为优势函数的无偏估计:

但是, 在训练过程中, 这个 往往无法完全正确评估出策略 的价值, 所以上述这种估计是有偏的, 也即如果我们使用TD error去近似优势函数, 就会引发系统性偏差。这样讲可能比较抽象, 我们来看具象化地解释下。
(1)方差与偏差

-
低方差,低偏差: E(射击点) = 靶心,且射击点密集分布在靶心周围。此时我们随机选一个射击点就能很好代表靶心 -
高方差,低偏差: E(射击点) = 靶心,但射击点们离靶心的平均距离较远。此时随机一个射击点不能很好代表靶心,但我们却可以从足够多的射击点中估算靶心坐标 -
高/低方差,高偏差: E(射击点)!=靶心,无论你做多少次射击,你都估计不准靶心的位置。
对于优势函数我们有 , 我们可以把 当作是蓝色的靶心, 而红色的点就是我们针对某个 做多次采样, 得到的一个个 。
-
当 能准确估计策略 的价值时, 至少是属于左侧”低偏差”这种情况。 而对于方差它则是由这里的两个随机变量 决定的,之所以说它们是随机变量,是因为在采取某个状态对 的情况下, 会转移到哪个 是确定的, 带来的奖励 也是不确定的。 -
当 不能准确估计策略 的价值时, 属于右侧”高偏差”这种情况。即红点的分布已经偏离,无论你采样再多次,你也无法估算真正的优势函数。
为了解决因为 估计不准而引发的”高偏差”问题, 直观上我们可以尽量少信任 的策略, 即对于 , 我们可以把 做递归地展开, 得到:
其中, 都是我们某次采样得到的即时奖励数据。如果 不准, 那么我就信任我的实际采样结果, 这样至少不会让我对优势函数的估计出现偏差。
但采取这种做法又会引发一个新问题: 我们知道 它们都是随机变量, 相比之前只用 , 现在的做法带来的随机性更大了(相当于在每一个timestep都引入了随机性,随机性逐步累加)。也就是如果之前的方差是 , 那么现在的方差则变成更大的 。最终, 你把 从上图的右侧纠正了上图的【高方差、低偏差】的位置。这意味着此时虽然偏差降低了,但你需要采样足够多的数据才能准确估计出优势函数,这样加重了实际训练中的采样负担。
那要怎么办呢?
(2)GAE
(排不动latex的版了,这边开始我就放我的笔记截图了😢😢)

8.4 PPO前身:TRPO

8.5 PPO做法1:PPO-Clip

8.6 PPO做法2:PPO-Penalty

8.7 PPO中的critic loss
在PPO的原始论文中,其实并没有对critic和actor拆分成两个网络以后的critic loss形式做详细介绍,所以这部分的解读我直接以deepspeed-chat的rlhf实现为例,将以下critic loss的实现。
我们知道,PPO的更新步骤是
# 对于每一个batch的数据
for i in steps:
# 先收集经验值
exps = generate_experience(prompts, actor, critic, reward, ref)
# 一个batch的经验值将被用于计算ppo_epochs次loss,更新ppo_epochs次模型
# 这也意味着,当你计算一次新loss时,你用的是更新后的模型
for j in ppo_epochs:
actor_loss = cal_actor_loss(exps, actor)
critic_loss = cal_critic_loss(exps, critic)
actor.backward(actor_loss)
actor.step()
critc.backward(critic_loss)
critic.step()


(文:极市干货)
