

在工业界实际的搜广推系统中,一个模型通常需要兼顾多个目标。例如,在通用搜索场景中,需要兼顾 CTR、相关性、商业化效率等目标;在电商推荐中,需要同时兼顾成交效率、丰富性等目标。
在实践中,我们发现,绝大多数目标之间或多或少都存在目标冲突的问题,多个目标之间往往不能兼得。例如,在电商推荐系统中,如果希望最大化成交效率,通常在丰富性上会有较大的损失。一个更常见的例子是广告收入和自然流量效率之间的矛盾,两者的此消彼长几乎存在于所有广告系统中。
常见的解决方案是一个多目标学习策略(Multi-task Learning, MTL),即在损失函数中,同时加入多个目标的 loss,并使用 loss 的权重来调整不同目标对模型带来的影响。然而,权重调整是一个费心费力的工作,经常会出现“面多了加水,水多了加面”这样的重复劳动。
此外,多目标学习中,没有考虑到目标之间的优先级,如果存在一个高优先级、牢不可破的目标,那么加入的次优先级的目标几乎一定会破坏高优先级目标的学习。这样一来,就无法保证高优先级目标的不可破坏性。
举一个简单的例子,我们希望同时兼顾系统的相关性和广告收入。我们的目标是在用户体验(即相关性)不受影响的情况下,尽可能最大化广告收入。基于权重调整的方法就会尝试不同的广告收入对应的权重。
然而,这种权重的调整是极其困难的,通常会出现权重过大就影响了相关性、权重过小就不能最大化广告收入这一尴尬境地。并且,如果目标增多至三个、四个,这种权重调整的方法就会变得无比困难。

论文标题:
No More Tuning: Prioritized Multi-Task Learning with Lagrangian Differential Multiplier Methods
https://arxiv.org/abs/2412.12092

建模:高优先级目标的强约束

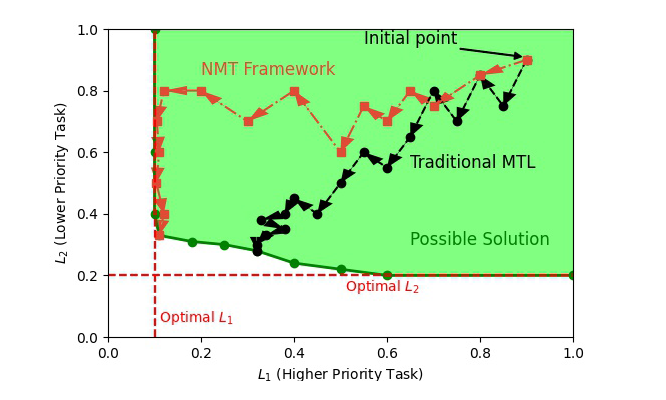
得到了上述问题,我们就需要在神经网络的框架下来求解这个带约束的优化问题。于是,我们把带优先目标的多目标优化建模成了两个阶段:
阶段 1 只需要使用标准的优化流程(如梯度下降)即可解决。但对于阶段 2,基于梯度的方法无法直接优化带约束的优化任务。在 2.2 中我们将重点讨论如何在目前基于梯度的优化框架下,优化带约束的最优化任务。

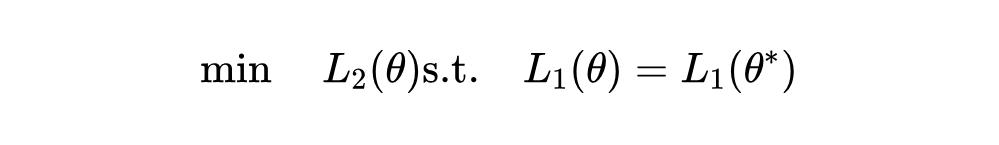
解决带约束的优化问题,基本的思路就是把带约束的优化问题转化为无约束的优化问题。不难想到,我们可以用拉格朗日乘子法来解决这个问题。
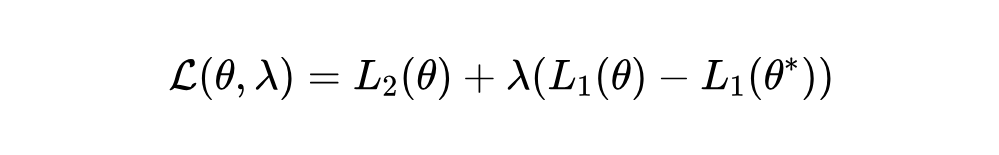
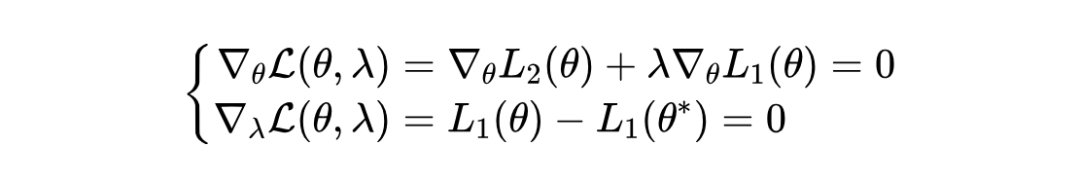
我们在论文中对这部分内容作了详细的理论分析,有兴趣的同学请参阅论文《No More Tuning: Prioritized Multi-Task Learning with Lagrangian Differential Multiplier Methods》的 Theoretical Analysis 一节。本文将不再对理论部分做深入探讨。
重缩放技巧
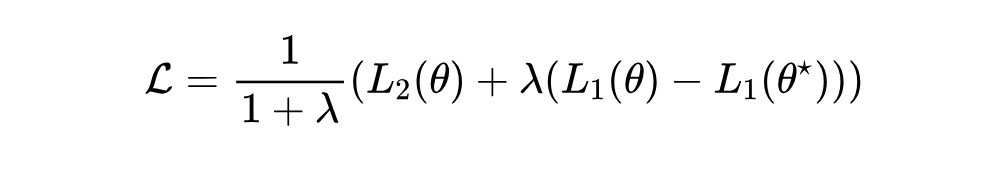

基于上述讨论,我们总结了 NMT 的总体流程。NMT 分为两个主要阶段:
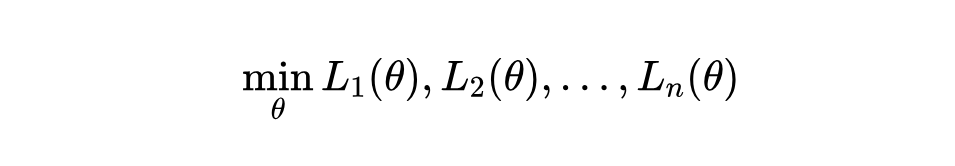
优化步骤如下:
4.针对后续任务继续该过程。
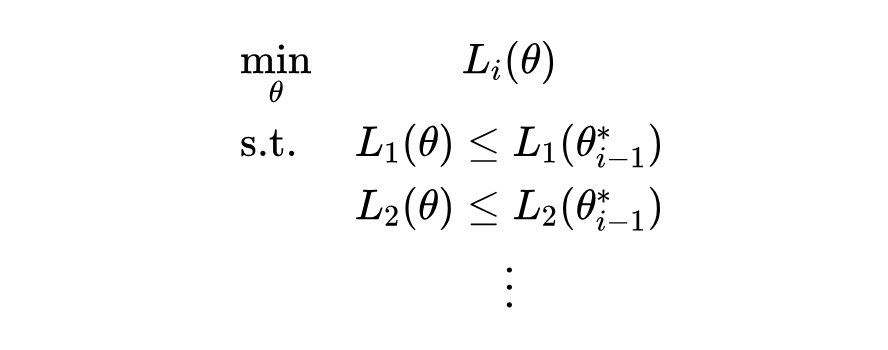
输入:
-
:模型参数的学习率 -
:拉格朗日乘子的学习率 -
:任务 的目标函数 () -
:拉格朗日乘子的初始值
-
使用 初始化 ,使用 初始化 ,其中 。 -
重复以下步骤直到收敛:
-
计算任务 的聚合损失: 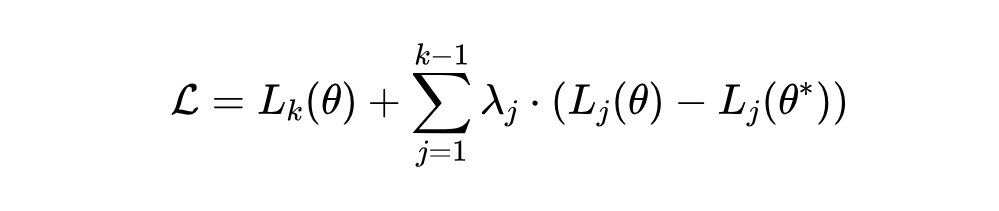
-
使用梯度下降更新 : -
使用梯度上升更新每个 : -
用优化后的 更新 。

Appendix: 代码实现
# clip for stability
diff = tf.clip_by_value(primary_loss - optimal_primary_loss, clip_value_min=-1, clip_value_max=1)
# update lambda
# lagrange_lr is a hyper-parameter
lagrange_mul = tf.assign(lagrange_mul, tf.clip_by_value(tf.assign_add(lagrange_mul, training_config.lagrange_lr * diff),
clip_value_min=0,
clip_value_max=training_config.lagrange_clip))
lagrange_loss = self.lagrange_mul * (primary_loss - optimal_primary_loss)
# use re-scaling method
final_loss = (secondary_loss + lagrange_loss) * (1 / (1 + self.lagrange_mul))
# clip for stability
diff = tf.clip_by_value(primary_loss - optimal_primary_loss, clip_value_min=-1, clip_value_max=1)
# update lambda
# lagrange_lr is a hyper-parameter
lagrange_mul = tf.assign(lagrange_mul, tf.clip_by_value(tf.assign_add(lagrange_mul, training_config.lagrange_lr * diff),
clip_value_min=0,
clip_value_max=training_config.lagrange_clip))
lagrange_loss = self.lagrange_mul * (primary_loss - optimal_primary_loss)
# use re-scaling method
final_loss = (secondary_loss + lagrange_loss) * (1 / (1 + self.lagrange_mul))
(文:PaperWeekly)
