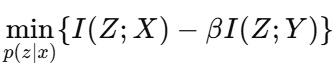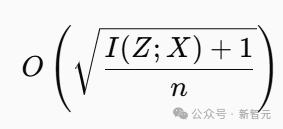【新智元导读】一家总部位于美国加州的初创公司Tilde,正在构建解释器模型,解读模型的推理过程,并通过引导采样动态调整生成策略,提升大语言模型的推理能力和生成精度。相比直接优化提示的提示工程,这一方法展现出更灵活高效的潜力,有望重塑AI交互方式。
可解释性是人工智能领域中的一个核心挑战,也是一个备受关注的问题。随着AI模型(尤其是深度学习模型)的规模和复杂性不断增长,模型内部的计算过程变得越来越难以理解。
但一直以来,模型的可解释性好像不如模型的性能那般受重视,往往不是新产品发布的宣传重点。
而最近,一个总部位于美国加州的AI初创Tilde宣布成立,专为模型可解释性而生。
他们正在构建解释器模型和控制技术,以解锁模型的深层推理和指令能力,从而实现新一代的人机交互。
当今AI的交互依赖于黑箱提示,这种方式本质上有损信息。试想在没有源代码的情况下优化一个软件系统——不仅低效,而且极度受限。
Tilde希望通过应用可解释性超越这些限制:他们正在构建解决方案,使人们能够直观地看见模型的内部工作机制,以直接引导模型行为并提升性能,超越传统的后训练方法或微调方法的潜能。
目前,基于已有的开源大语言模型、文生视频模型,他们的解释器模型已经实现了大语言模型的推理能力改进,并在文本生成视频模型中实现了更精细的生成控制。
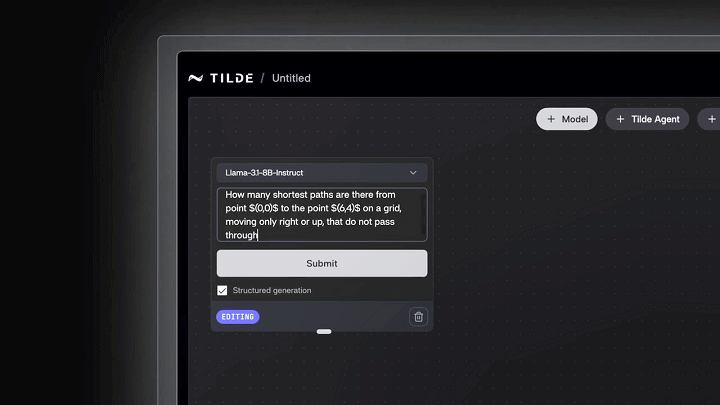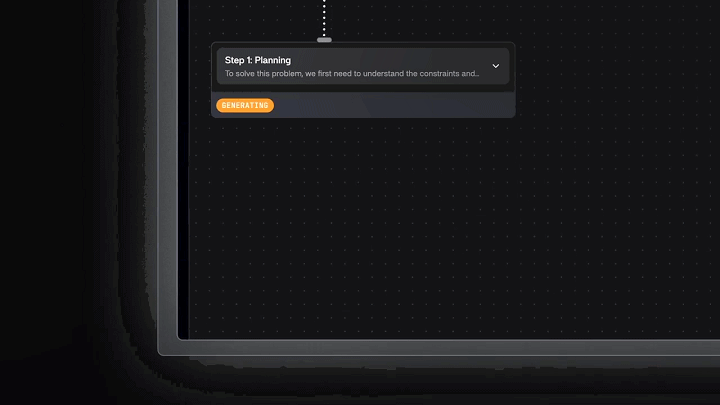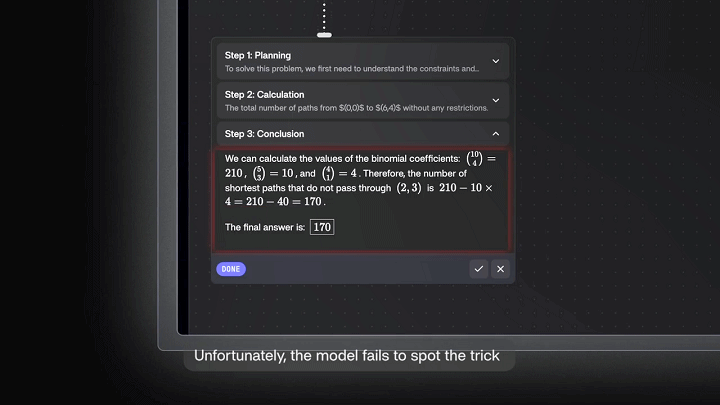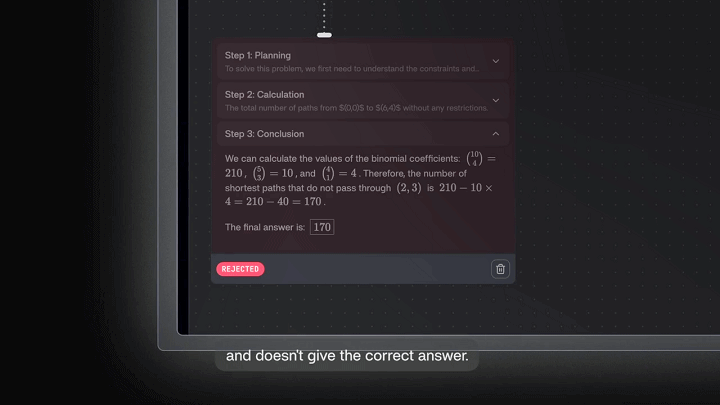
关于大语言模型推理能力的优化,视频中提到了一个案例,让Llama 3.1 8B尝试解答一个可以通过巧妙数学技巧解决的脑筋急转弯:
从点(0,0)到点(6,4)的网格上,若只能向右或向上移动,有多少条最短路径不经过点(2,3)?
问题输入后,Llama 3.1 8B输出了一个错误的答案。
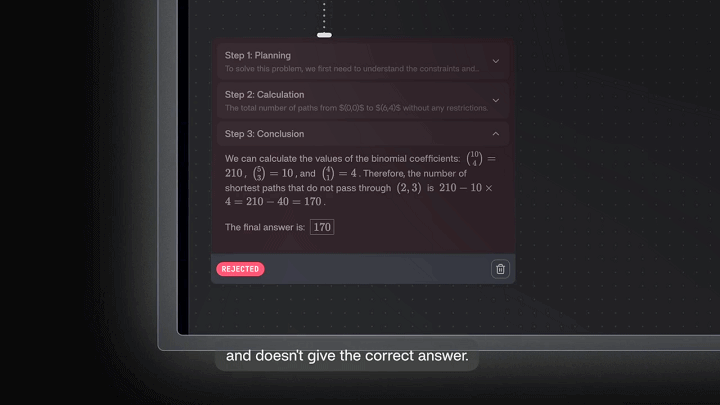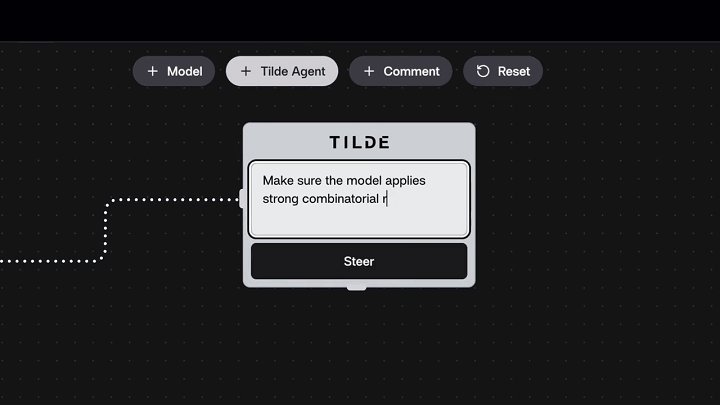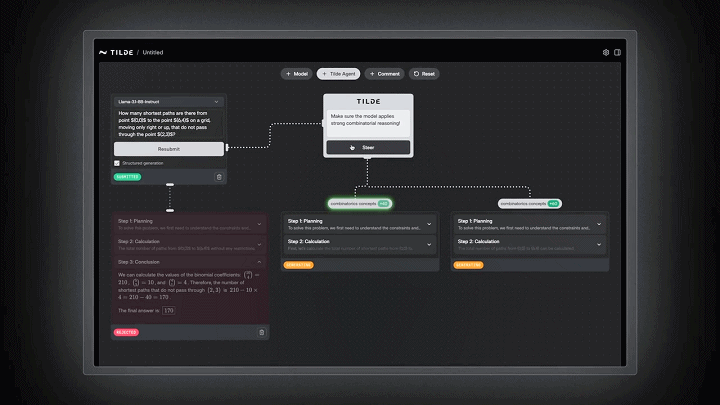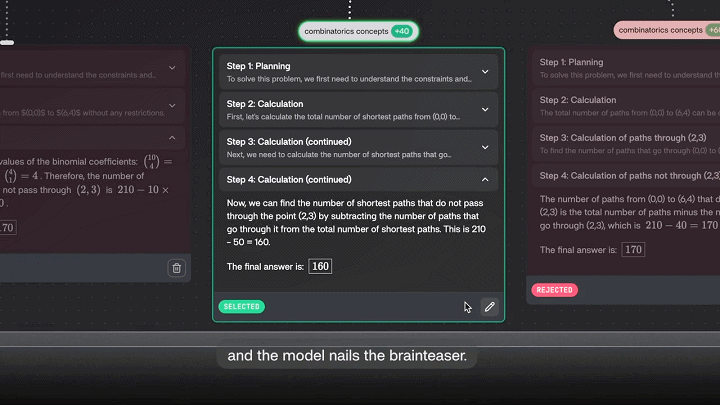
接着,案例演示引入了Tilde的干预,补充了指令:「确保模型应用强大的组合推理!」
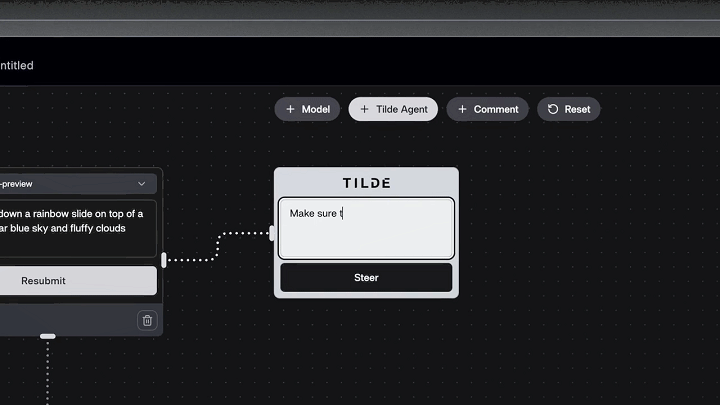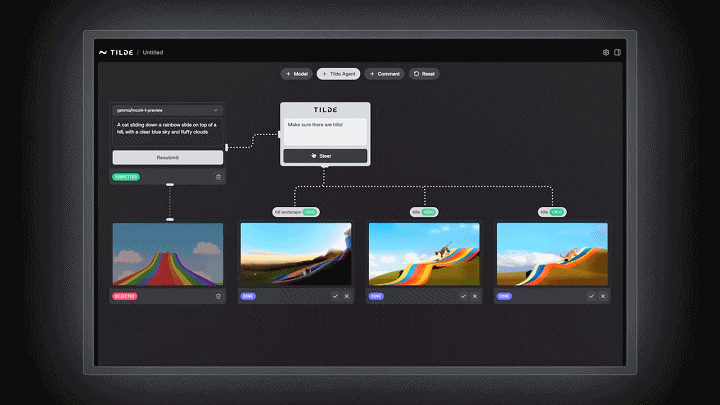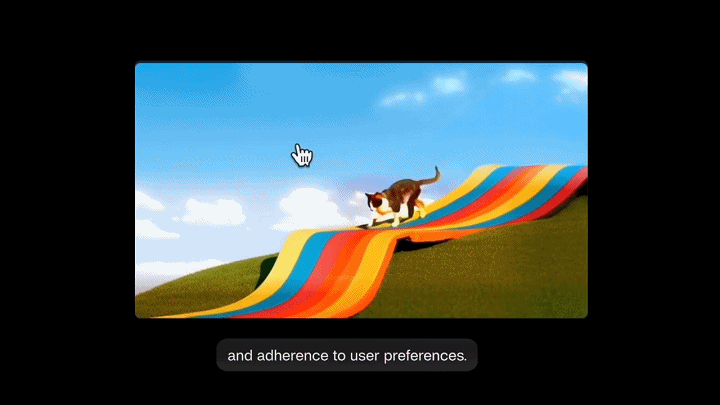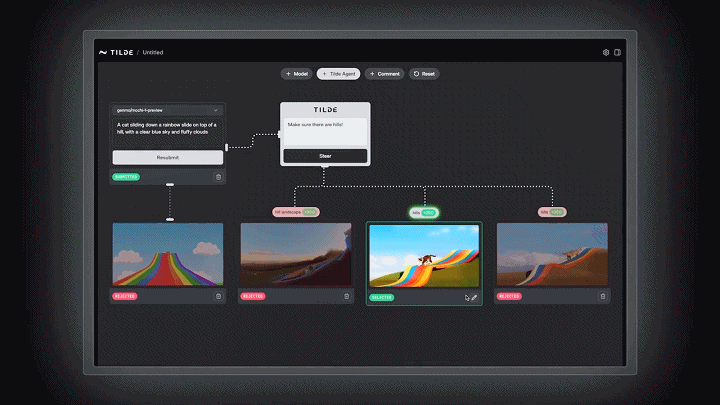
而至于文本生成视频模型更精细的生成控制,视频给到的案例中,向Genmo的mochi 1输入了指令:
一只猫从山顶的彩虹滑梯上滑下来,天上有湛蓝的天空和蓬松的云朵。
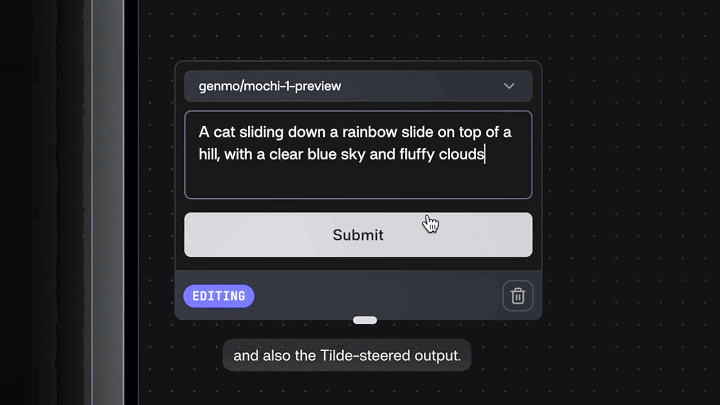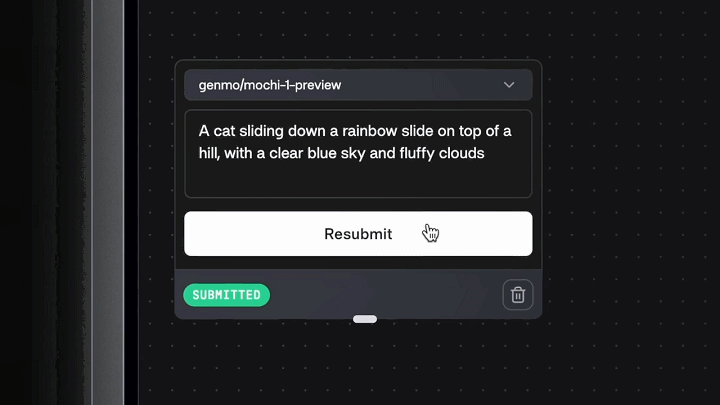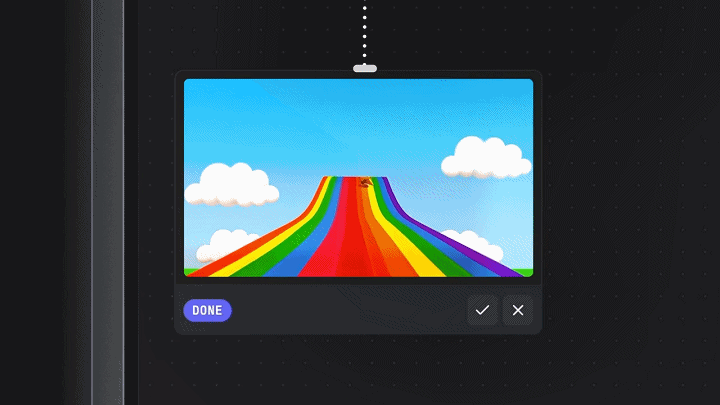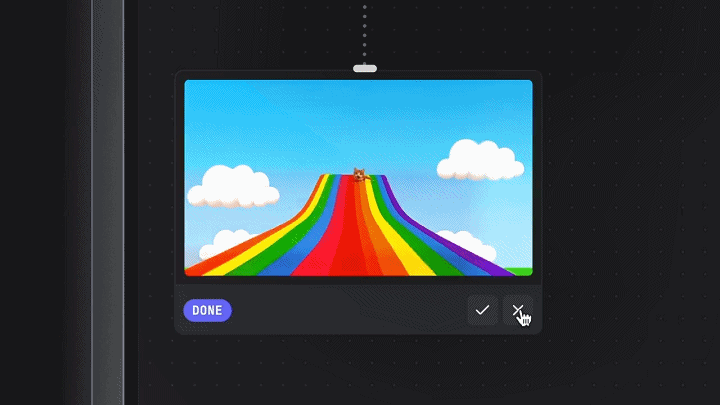
接着,案例演示引入了Tilde的干预,补充了指令:「确保有山!」
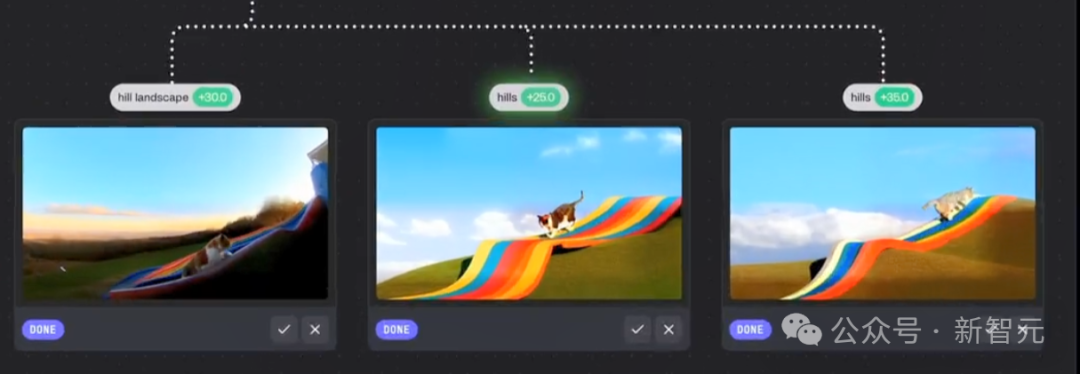
我们可以注意到加入Tilde干预后的准确性和遵循用户偏好的提升。可以看到三个优化后的图像中:第一张更注重于山间风景的加强;第二、三张的区别不太大,第三张的坡形相对更明显一些。
网友讨论
看到这里,有网友不禁提问:这和提示工程有什么区别?
谷歌DeepMind高级研究科学家Neel Nanda就提到:「关于组合数学问题的例子,如果你在提示的末尾添加『请使用强大的组合推理』(please use strong combinatorial reasoning),会发生什么?」
前OpenAI研究员Neil Chowdhury回复道:「我在Llama-3.1 8B-Instruct(默认的Hugging Face采样参数)上尝试了这个方法,它解决了问题——不过当然,我希望能看到更深入的分析 🙂 」
Neel Nanda还艾特了Tilde的X账号,表示很想看到他们的工具和提示工程(prompt modification)基准方法进行合理的比较。
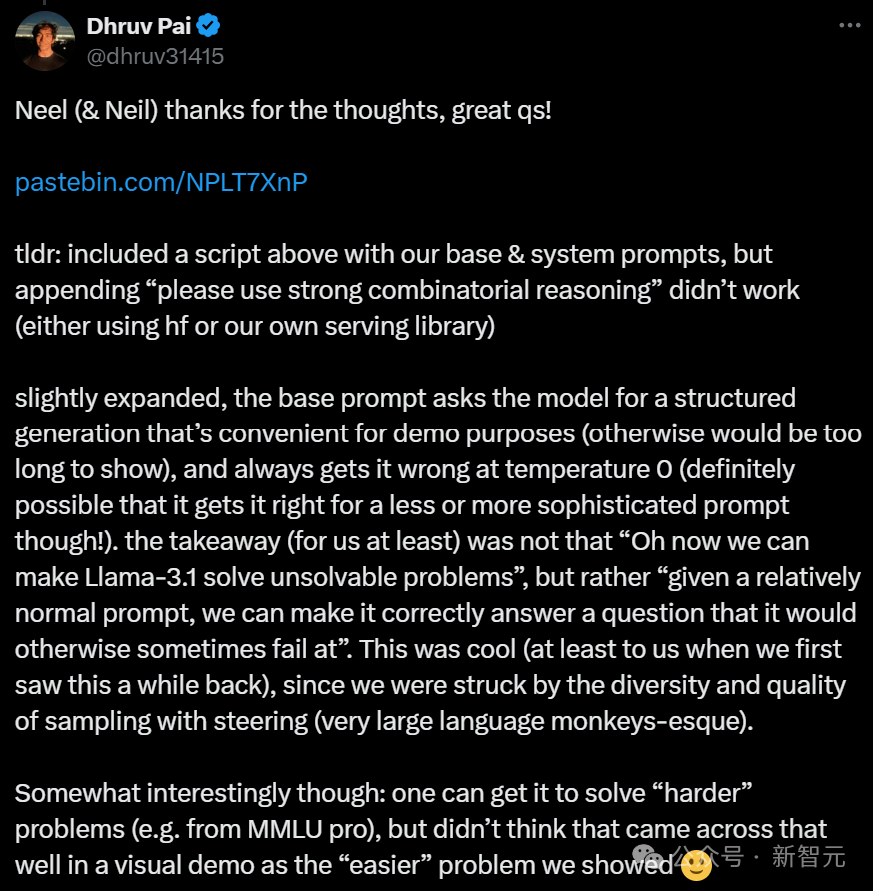
Tilde的创始人之一Dhruv Pai对此进行了回复——
Neel(以及Neil),谢谢你们的想法,提出了好问题!
简而言之:上面包含一个脚本,展示了我们使用的基础和系统提示,但在末尾添加「请使用强大的组合推理」并没有奏效(无论是使用Hugging Face还是我们自己的服务库)。
稍微展开说明一下:基础提示要求模型生成一个便于演示的结构化输出(否则生成内容会太长),而且在温度为0的情况下总是出错(也可能对更复杂或更简单的提示能成功,但未测试)。
我们的结论并不是「哦,现在我们可以让Llama-3.1解决无法解决的问题」,而是「在一个相对普通的提示下,我们可以让它正确回答一些本来可能会失败的问题」。
这对我们来说很有趣,因为我们第一次看到时,被这种引导采样(Steering Sampling)的多样性和质量(有点类似于非常智能的大型语言模型)惊艳到了。
有趣的一点:虽然引导可以让它解决更难的问题(例如MMLU专业问题集的题目),但我们认为在演示中这种「更难的问题」没有「我们展示的更简单的问题」表现得那么直观。🙂
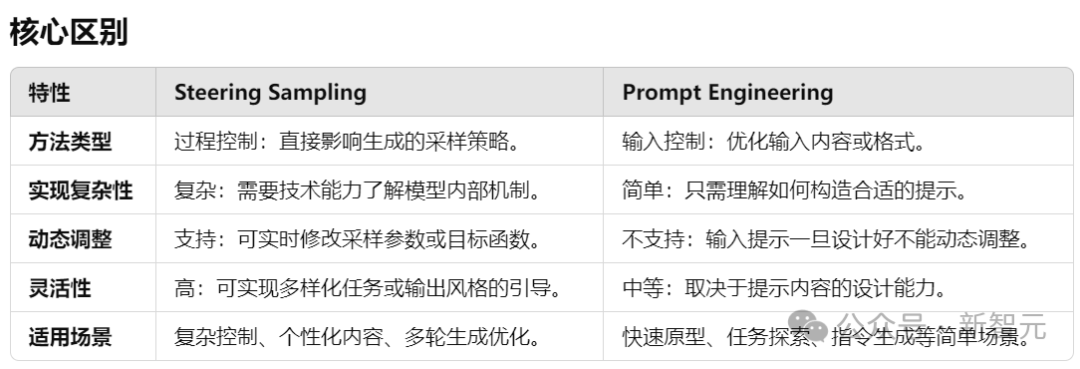
引导采样 VS 提示工程
引导采样(Steering Sampling)和提示工程(Prompt Engineering)是两种不同的方法,用于控制LLM的输出方向。它们的目标都是生成符合需求的结果,但所关注的技术和实现方式有所不同。
引导采样通过调整模型内部的采样策略或生成过程,在模型生成的过程中动态引导输出的方向,而不是直接改变输入的提示。
而提示工程通过优化或设计输入提示(prompt)的内容或结构,来引导模型按照预期方式生成输出。
不过,目前在Tilde的官网中并没有找到视频案例中展示的产品界面,只找到了一个已经上线的产品「Stargazer」,主要围绕大语言模型的可解释性而生,可用于探索开源Llama模型内部。
体验地址:https://stars.tilderesearch.com/
Stargazer基于Llama 3.1 8B设计。
向模型提问时,它的回答会被拆分成多个token(文本块)。
之后,点击回答中的任意token,就能查看该token的stars(相关概念)和constellations(概念群组)。这些是模型思维的快照。
Stargazer还对stars按照稀有程度进行了分类:Common(稀有程度0-35%)、Rare(稀有程度35-45%)、Ultra(稀有程度45-60%)、Legendary(稀有程度60-100%)。
以下是分别用中英文向Stargazer提问「什么是语言模型/What is a language model」时,它给到的答案和分词结果。
Tilde还发表了一篇内容关于稀疏自编码器中的速率-失真问题的博客,并表示不久将会发布开源的项目。
博客中详细探讨了稀疏自动编码器(SAE)、Top-k激活函数和信息瓶颈框架,它们都涉及如何更高效地组织和控制模型的内部机制。这些理论都被积极融入到Tilde训练的解释性模型中。
博客地址:https://www.tilderesearch.com/blog/rate-distortion-saes
稀疏自动编码器
稀疏自动编码器是一个令人兴奋的研究领域,它不仅有助于我们理解深度学习中的特征表示,还为开发更高效且更可解释的模型提供了方向。
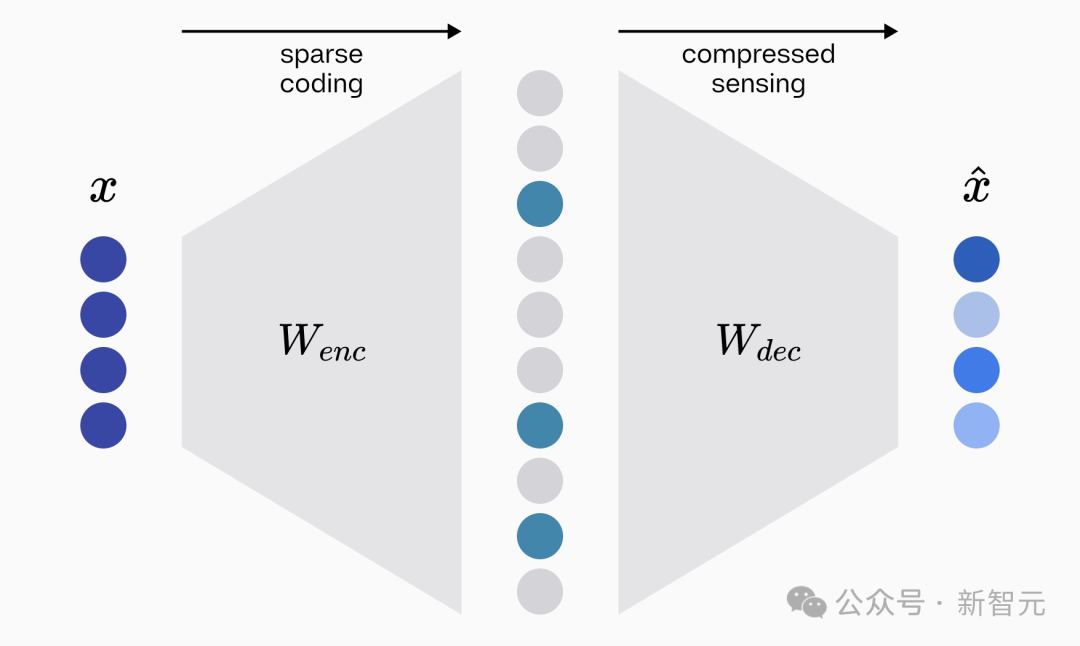
从可解释性角度退一步来看,构建一个有效的稀疏自动编码器(SAE)需要解决两个基本问题:创建高效表示数据的稀疏编码,以及从这些编码中准确重建原始数据。
第一个任务由自动编码器的编码器矩阵完成,将输入数据(如图像或文本)转换为一种高效且稀疏的表示形式;第二个任务由解码器矩阵完成,需从编码后的稀疏表示中重建原始输入,验证编码器选择的信息是否足够全面。稀疏编码可以看作模型如何「理解」输入的快照。
编码器和解码器两者共同作用,既提升了模型的效率,又为分析其内部工作机制提供了透明窗口,是实现可解释性的重要基础。
从根本上说,构建一个有效的稀疏自动编码器需要解决的两个基本问题分别属于稀疏编码(sparse coding)理论和压缩感知(compressed sensing)领域。
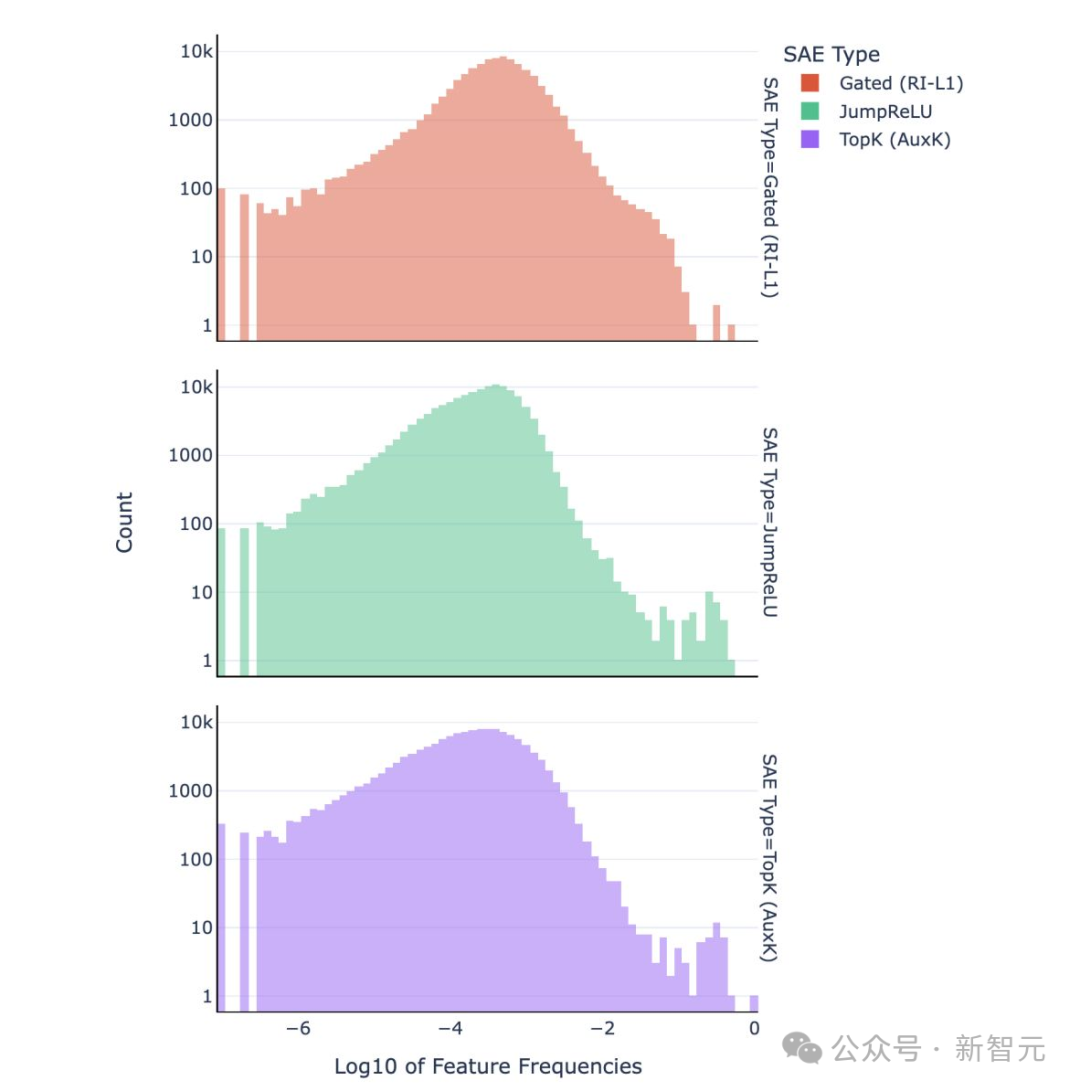
稀疏编码理论还关注「负载均衡」。它强调稀疏编码中激活应在不同特征或神经元之间均匀分布。某些研究,如Top-k和JumpReLU架构,发现了严重的特征频率失衡问题:某些特征的高频触发会导致字典难以解释。通过负载均衡正则化可以减轻这一问题,并改善字典的可解释性。
Tilde目前正在积极研究基于这些理论的新型架构。
通过IB框架理解Top-k方法
最后,博客从信息瓶颈(Information Bottleneck, IB)理论的角度审视Top-k方法。
在训练稀疏自动编码器时,激活函数的选择对字典的稀疏性和学习动态有着重要影响。
传统上,可以使用ReLU激活函数配合ℓ1正则化,将字典学习视为一个多约束问题:网络需要同时平衡重建误差和稀疏性惩罚。在这种方法中,稀疏性是自适应的——输入越复杂,潜在激活越多,反之亦然。
Top-k方法消除了这种复杂性,直接固定所有输入的稀疏性水平。它不再需要在稀疏性损失和重建误差之间权衡,而是只优化重建误差。
Top-k激活函数在稀疏自动编码器中的高效性可以通过信息瓶颈框架来理解。该框架平衡了信息保留与压缩:
1. 希望最小化输入X与表示Z的互信息I(Z;X),减少冗余;
2. 同时最大化Z与目标Y的互信息I(Z;Y),保留对重建有用的信息。
通过固定输入中活动神经元的数量,Top-k方法直接对I(Z;X)施加上限,从而限制了信息流动,并自然优先选择最具信息量的特征进行重建。与传统方法平衡稀疏性惩罚和重建的方式不同,Top-k的硬约束简化了这一动态,仅在设定的稀疏性水平内优化重建精度。
Top-k方法内置了瓶颈效应:通过减少I(Z;X) ,可能提高泛化能力,因为它限制了信息流动。这与泛化理论中的发现一致,该理论将模型复杂性与泛化误差联系起来:
实际上,Top-k方法强制实施了一种率失真约束,驱使网络优先考虑稳定性和信号保留,而非噪声。Tilde研究团队在实验中发现,与自适应稀疏方法相比,Top-k方法能够产生更平滑的学习动态和更强的抗噪性。
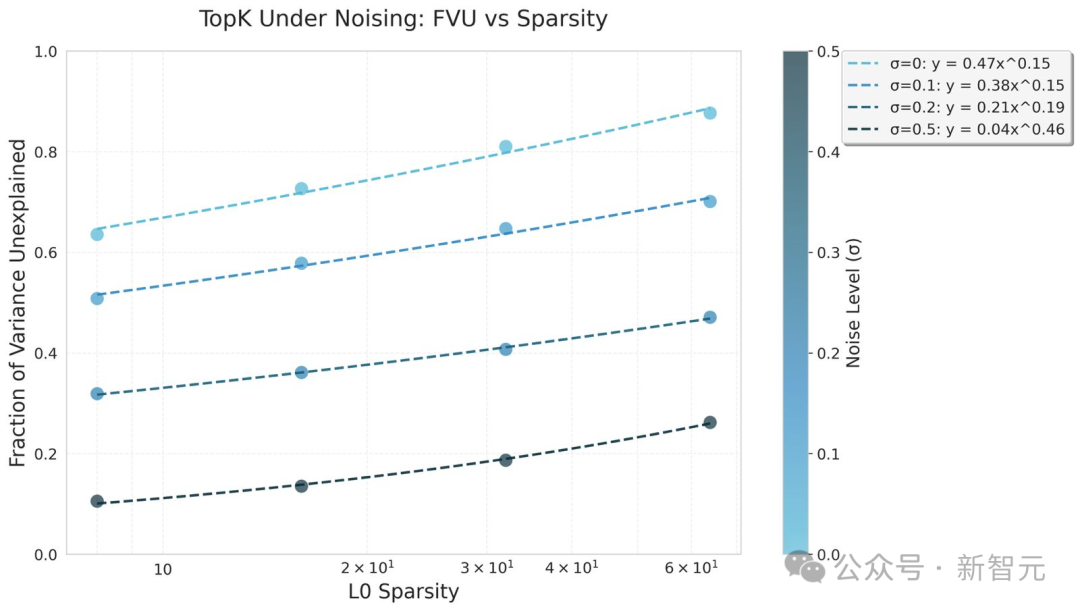
他们在CIFAR10数据集上训练了Top-k自动编码器50个周期,并施加了不同的高斯噪声条件。假设,架构所施加的信息瓶颈能够提高在高噪声环境下的鲁棒性。
在高斯噪声条件下的Top-k缩放定律中,信息瓶颈显著提升了Top-k的鲁棒性。实验发现,Top-k在较高噪声环境中,幂律拟合的系数有所增加,表明更大的k值能够更好地从噪声中恢复信号。此外,训练动态高度稳定,损失几乎单调收敛。
与之相对比,在高噪声设置下测试的ReLU基准模型却出现了崩溃或发散现象,因此被排除在图表之外。
该理论为理解稀疏编码如何在压缩和重建之间权衡提供了框架。在未来的研究中,Tilde将进一步探讨这一方向,并期待为解码器架构提供新的优化方法。
(文:新智元)