
新智元报道
新智元报道
【新智元导读】小模型也能击败o1?微软全华人团队提出rStar-Math算法,三大革命性技术突破,不仅让SLM在数学推理能力上刷新SOTA,更是挤进了全美20%顶尖高中生榜单。
一夜之间,微软用小模型(SLM),在数学推理上击败o1,冲爆了AI社区热搜。
不仅如此,SLM在美国数学奥林匹克(AIME)上,拿下了53.3%的亮眼成绩,直逼全美20%顶尖高中生!
瞬间,大波Reddit网友在线发出灵魂拷问,「我们将在25年年终前就会有AGI了,不是吗」?
HugginFace CEO发文,rStar-Math成为HF热门论文
这篇论文究竟做出了怎样的技术创新,能让o1甘拜下风?
论文中,来自微软亚研院的全华人团队,提出了全新算法rStar-Math,证明了SLM无需从高级模型蒸馏,就能在数学推理上,媲美甚至一举超越o1。

论文链接:https://arxiv.org/pdf/2501.04519
rStar-Math核心在于,让小模型具备「深度思考」的能力。
团队借鉴了AlphaGo中蒙特卡洛树搜索(MCTS)技术,设计了一个由2个协同工作的SLM组成的系统:
-
一个数学策略小语言模型(SLM)
-
一个过程奖励模型(PRM)
此外,rStar-Math具体设计中,引入了三项技术创新:全新代码增强CoT数据合成;全新PRM训练方法;自我进化方案。
通过4轮自我进化,并结合数百万个为747k数学问题合成的解答,rStar-Math让SLM数学推理能力刷新SOTA。
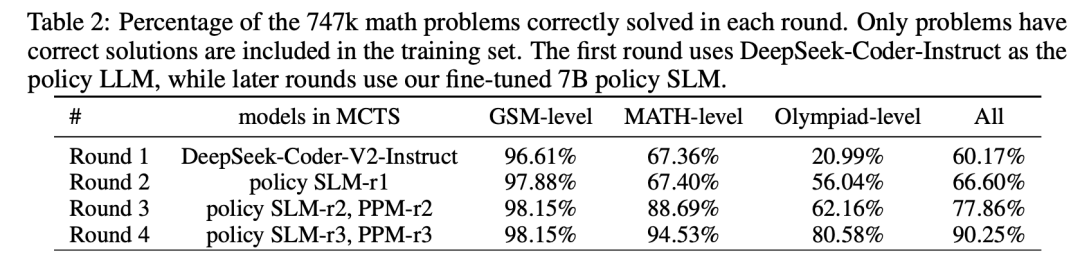
在MATH基准测试中,它将Qwen2.5-Math-7B的成绩从58.8%提升至90.0%,将Phi3-mini-3.8B的成绩从41.4%提升至86.4%,比o1-preview分别高+4.5%和+0.9%。
在美国数学奥林匹克(AIME)上,rStar-Math解决了平均53.3%(8/15)的题目,排名位于高中数学优等生前20%。具体结果如下所示。
Keras之父预言道,2025年将会不断涌现这样的研究,通过结合程序搜索、CoT搜索,在LLM指导下提升推理基准(包括ARC和数学基准)的表现。
MCTS、遗传搜索,你能想到的方法,都会被尝试。

数学推理难在哪儿?
在测试时计算scaling新范式中,关键是训练一个强大的策略模型来生成有前景的解答步骤,以及一个可靠的奖励模型来准确评估这些步骤,这两者都依赖于高质量的训练数据。
众所周知,在数学推理中,正确的最终答案并不能确保整个推理过程的正确性。错误的中间步骤会显著降低数据的质量。
然而,策略模型很难区分出来推理步骤到底正确还是错误的,从而很难去剔除低质量数据。
与此同时,能够对中间步骤提供细粒度反馈的奖励模型,训练数据更加稀缺:准确的逐步反馈需要大量的人力标注,难以大规模扩展,而自动标注由于奖励分数的噪声,取得的效果有限。
由于上述问题,现有的训练策略模型使用基于蒸馏的合成数据,如扩展GPT-4蒸馏的CoT数据,但回报越来越少,无法超越其教师模型的能力;同时,至今为止,训练可靠的PRM来进行数学推理仍然是一个开放问题。
rStar-Math,三大创新
与依赖更强大的LLM合成数据不同,rStar-Math利用小语言模型(SLM)结合蒙特卡洛树搜索(MCTS)建立了自我进化过程,迭代生成更高质量的训练数据。
为了实现自我进化,rStar-Math引入了三项关键创新。

新CoT数据合成方法
首先,全新代码增强型CoT数据合成方法, 将数学问题求解被分解为MCTS中的多步骤生成。在每一步中,作为策略模型的SLM会对候选节点采样,每个节点生成一个单步的CoT推理和相应的Python代码。
为了验证生成质量,只有那些成功执行Python代码的节点会被保留,从而减少中间步骤中的错误。
此外,多步MCTS回合会根据每个步骤的贡献自动分配Q值:那些贡献更多推理轨迹并导向正确答案的步骤会获得更高的Q值,并被认为是更高质量的。这确保了SLM生成的推理轨迹由正确且高质量的中间步骤组成。
过程偏好模型
第二,引入了一种新颖的方法,训练一个作为PPM的SLM,旨在实现所需的PRM,该模型能够可靠地预测每个数学推理步骤的奖励标签。
PPM利用了这样一个事实:尽管使用广泛的MCTS回合,Q值仍然不足以精确评分每个推理步骤,但Q值可以可靠地区分正向(正确)步骤和负向(无关/错误)步骤。
因此,训练方法基于Q值为每个步骤构建偏好对,并使用成对排名损失来优化PPM对每个推理步骤的评分预测,从而实现可靠的标注。
这种方法避免了传统方法直接使用Q值作为奖励标签,因为这些方法在逐步奖励分配中固有地存在噪声和不精确。
自我进化
最后,四轮自我进化的方案逐步从0构建前沿策略模型和PPM。
研究人员从公开可用的来源中,策划了一个包含747,000个数学题的数据集。
在每一轮中,使用最新的策略模型和PPM执行MCTS,利用上述两种方法生成越来越高质量的训练数据,以训练更强的策略模型和PPM用于下一轮。
每一轮都实现了逐步的改进:(1)更强的策略SLM,(2)更可靠的PPM,(3)通过PPM增强的MCTS生成更好的推理轨迹,以及(4)改进训练数据覆盖范围,解决更多高难度的甚至是竞赛级别的数学问题。
四轮自我进化
由于SLM的能力较弱,要进行四轮MCTS深度思考,可以逐步生成更高质量的数据,并通过更多高难度的数学问题来扩展训练集。
每轮都要用MCTS生成逐步验证的推理轨迹,然后用这些轨迹训练新的策略SLM和PPM。新模型随后应用于下一轮,以生成更高质量的训练数据。
第一轮:启动初始强策略SLM-r1
为了使SLM能够自我生成合理的训练数据,要执行一轮引导训练,微调初始的强策略模型,记作SLM-r1。
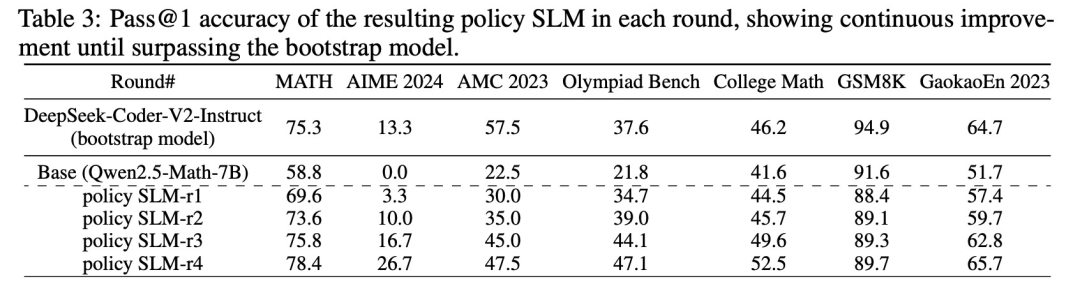
如表2所示,使用DeepSeek-Coder-V2-Instruct(236B)运行MCTS,收集SFT数据。
在这一轮中,由于没有可用的奖励模型,因此使用终端引导注释来标注Q值,并将MCTS的回合数限制为8,以提高效率。对于正确的解答,选择Q值平均值最高的前两条轨迹作为SFT数据。
第二轮:训练可靠的PPM-r2
在这一轮中,使用更新后的7B策略模型SLM-r1,进行大量的MCTS回合以获取更可靠的Q值标注,并训练了第一个可靠的奖励模型PPM-r2。其中,为每个问题执行16轮MCTS回合。生成的逐步验证推理轨迹在质量和Q值精确度上都有显著提升。
如表3所示,策略SLM-r2如预期般得到改进;类似的,如表4所示,PPM-r2也比引导轮中的表现更为有效。
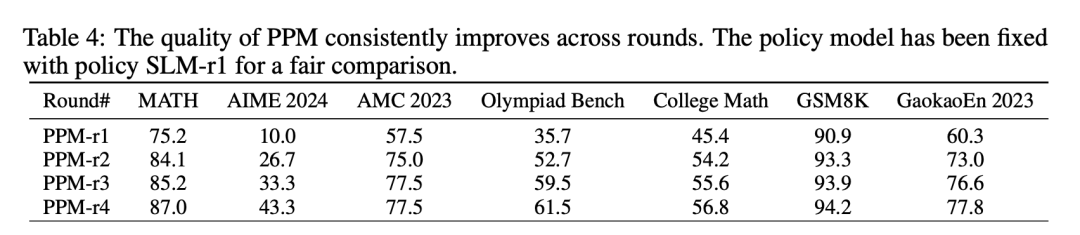
第三轮:使用PPM增强的MCTS显著提高数据质量
在这一轮中,借助可靠的PPM-r2,要执行PPM增强的MCTS以生成数据,从而生成了明显更高质量的推理轨迹,这些轨迹覆盖了训练集中更多的数学和奥林匹克级问题(表2)。
生成的推理轨迹和自注释的Q值随后被用于训练新的策略SLM-r3和PPM-r3,二者均表现出显著改进。
第四轮:解决高难度的数学问题
在第三轮之后,尽管基础学科和MATH问题已达到较高的成功率,但只有62.16%的奥林匹克级问题被纳入训练集。
为了提高覆盖率,采用了一种简单的策略:对于16轮MCTS回合后仍未解决的问题,增加执行64轮回合,必要时增至128轮。并对不同随机种子进行多次MCTS扩展。成功将奥林匹克级问题的成功率提高至80.58%。
在经过四轮自我进化后,747k数学问题中有90.25%成功被纳入训练集,如表2所示。在剩余的未解决问题中,绝大部分是合成问题。
作者随机检查了20个问题样本,发现其中19个被错误标注为错误答案。因此,得出结论,剩余未解决的问题质量较低,因此在第4轮结束时终止了自我进化过程。
小模型击败o1,攻克奥赛级难题
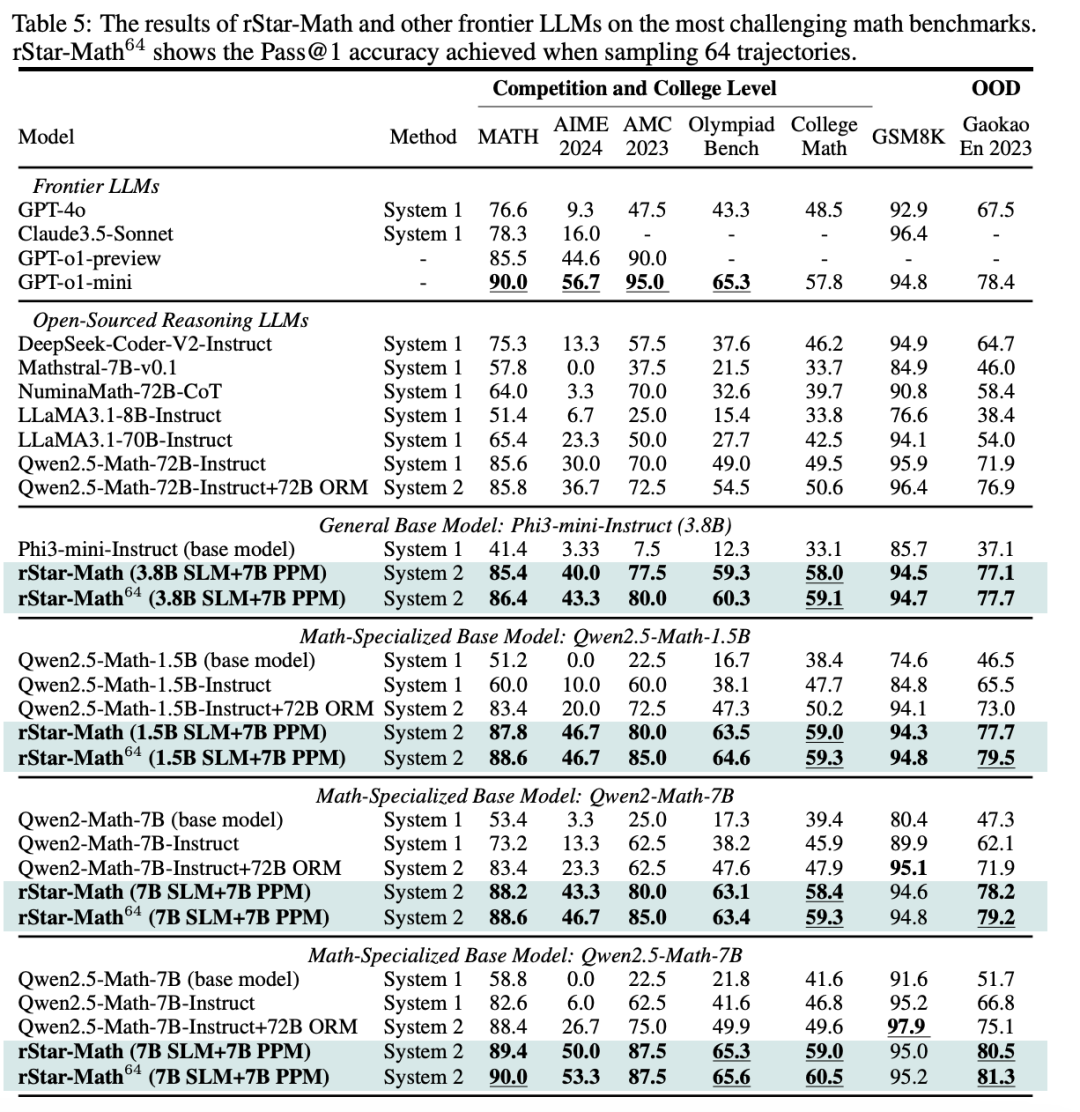
表5展示了rStar-Math与最先进推理模型的比较结果。有三点需要强调:
(1)rStar-Math显著提升了SLM数学推理能力,达到了与OpenAI o1相当或更佳的性能,同时模型规模大大缩小(1.5B-7B)。
(2)尽管使用了更小的策略模型(1.5B-7B)和奖励模型(7B),rStar-Math仍显著超越了最先进的系统2基准模型。rStar-Math持续提升了所有基础模型的推理准确性,达到最先进的水平。
(3)除了像MATH、GSM8K和AIME这样的知名基准,rStar-Math还在其他高难度的数学基准测试上表现出了强大的泛化能力,包括奥林匹克数学基准、大学数学和国内的高考数学试题。
扩展测试时计算
rStar-Math使用MCTS来增强策略模型,依据PPM引导搜索解决方案。通过增加测试时的计算量,可以探索更多的轨迹,从而间接地提高性能。
在图3中,通过比较在四个高难度的数学基准上,不同数量的采样轨迹下,官方Qwen Best-of-N的准确率,展示了测试时计算扩展的影响。
仅采样一条轨迹时,对应策略LLM的Pass@1准确率,表明模型回退到系统1的推理方式。
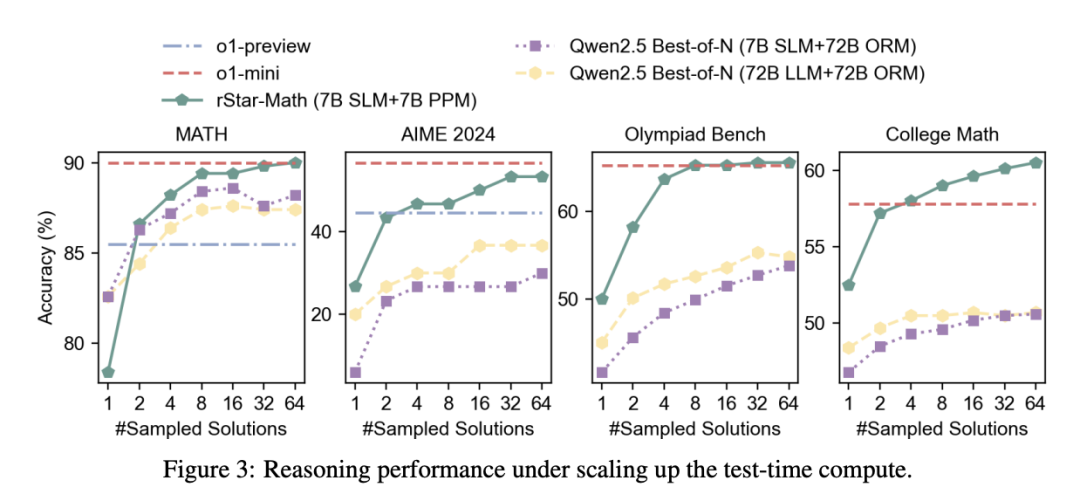
(1)仅使用4个轨迹,rStar-Math显著优于Best-of-N基准,超过了o1-preview并接近o1-mini。
(2)扩展测试时计算在所有基准上均提高了推理准确率,但提升趋势有所不同。在Math、AIME和Olympiad Bench上,rStar-Math在64个轨迹时表现出趋于饱和或提升缓慢,而在College Math上,性能持续稳步提升。
关键发现
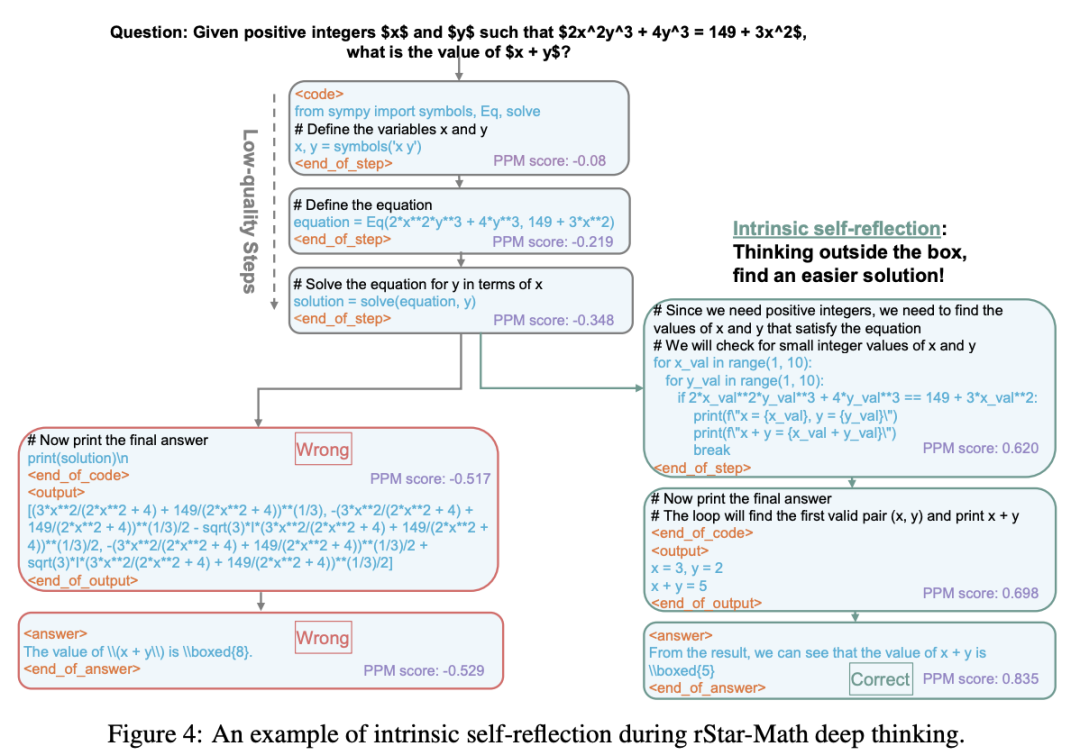
内在自我反思能力的出现
OpenAI o1的一个关键突破是其内在的自我反思能力。当模型出错时,它能够识别错误并通过正确的答案进行自我修正。然而,在开源的大语言模型中,这一能力通常表现得相当不好。
这次意外地观察到,MCTS驱动深度思考在问题求解过程中表现出自我反思。如图4所示,模型最初使用SymPy在前三步中形成一个方程,但会导致错误的答案(左分支)。
有趣的是,在第四步(右分支),策略模型意识到其早期步骤的质量较差,并避免继续沿着最初的问题求解路径走下去。相反,它回溯并使用一种新的、更简单的方法解决问题,最终得出正确答案。值得注意的是,并未包含任何自我反思训练数据或提示,这表明先进的系统2推理能够促进内在的自我反思。
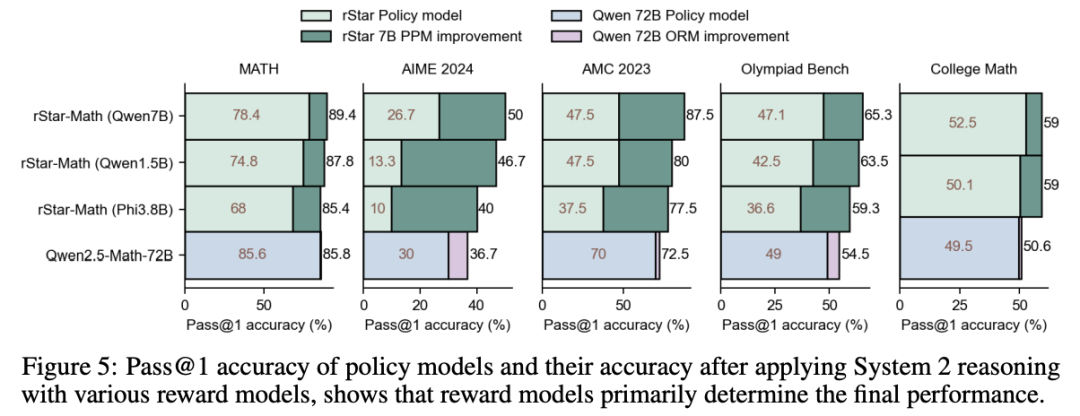
PPM决定了系统2的推理上限
实验表明,一旦策略模型的能力达到相对较强水平,决定性能上限的关键因素就是过程偏好模型(PPM)。图5总结了不同规模策略模型的准确性以及奖励模型带来的提升。
尽管由于训练策略、数据集和模型规模的差异,Pass@1准确性存在变化,但足以证明奖励模型是系统2推理中的主导因素。
PPM识别定理应用的步骤
在新的实验中,发现在rStar-Math的问题求解过程中,PPM能够有效地识别过程中关键的中间步骤。这些步骤通过高奖励分数进行预测,引导策略模型生成正确的解决方案。
泛化
rStar-Math提供了一种通用的方法,能提升LLM推理能力,适用于各种领域。
首先,rStar-Math可以推广到难度更高的数学任务,如定理证明。rStar-Math已展示了证明数学命题的潜力。
其次,rStar-Math还能够推广到其他领域,如代码推理和常识推理。特别是,生成逐步验证的训练轨迹需要一个机制来提供反馈,判断给定的轨迹是否在MCTS回合结束时达到了预期的输出。
论文也讨论了模型消融并在附录中给出了更多的实验细节或结果。
(文:新智元)
