BiDM团队 投稿
量子位 | 公众号 QbitAI
将扩散模型量化到1比特极限,又有新SOTA了!
来自北航、ETH等机构的研究人员提出了一种名为BiDM的新方法,首次将扩散模型(DMs)的权重和激活完全二值化。

具体而言,作者们从时间和空间的角度对扩散模型进行了优化:
从时间角度来看,引入了“时间步友好二值结构”(TBS),通过可学习的激活二值化器和跨时间步特征连接来应对DMs高度时间步相关的激活特征。
从空间角度来看,提出了“空间分块蒸馏”(SPD),目标是解决二值化特征匹配的困难,特别关注图像生成任务和噪声估计网络的空间局部性。
实验结果显示,W1A1 BiDM在LSUN-Bedrooms 256×256上的LDM-4模型上取得了22.74的FID分数,远远超越了当前状态的最先进通用二值化方法的59.44分,并实现了高达28倍的存储节省和52.7倍的操作效率提升。
下面具体来看。
现有扩散模型1位量化主要集中在「权重」
目前为止,扩散模型由于其高质量和多样化的生成能力,在图像、语音和视频等多个领域引起了极大的关注和应用。它可以通过多达1000步的去噪步骤,从随机噪声生成数据。
不过,虽然一些加速采样方法能够有效减少生成任务所需的步骤数量,但每个时间步的昂贵浮点计算仍然限制了该模型在资源受限场景中的广泛应用。

因此,对扩散模型的压缩成为其更广泛应用的关键步骤,现有的压缩方法主要包括量化、蒸馏、剪枝等。这些压缩方法的目标是在保持准确性的同时减少存储和计算成本。
其中,量化被认为是一种非常有效的模型压缩技术,通过将权重和/或激活量化为低位整数或二值化,实现紧凑存储和推理中的高效计算。
所以,已有一些研究将量化应用于扩散模型,以在保持生成质量的同时实现模型的压缩和加速。
而1位量化,即二值化,能够最大限度地节省模型的存储空间,并且在卷积神经网络(CNN)等判别模型中表现良好。此外,当权重和激活同时量化为1位时,如完全二值化,使用类似XNOR和bitcount的高效位运算可以替代矩阵乘法,达到最高效的加速效果。
一些现有的工作尝试将扩散模型量化为1位,但它们的探索主要集中在权重上,离完全二值化仍有较大距离。
实际上,对于扩散模型这样的生成模型,完全二值化权重和激活的影响是灾难性的:
a) 作为生成模型,扩散模型的丰富中间表示与时间步密切相关,而高度动态的激活范围在使用二值化权重和激活时受到严重限制;
b) 像扩散模型这样的生成模型通常需要输出完整的图像,但高度离散的参数和特征空间使得在训练过程中很难与真实值匹配。离散空间中的优化难度以及与时间步动态相关的表示能力不足,导致二值化扩散模型难以收敛,甚至在优化过程中崩溃。
提出BiDM:完全二值化「权重」和「激活」
面对上述不足,作者们提出了BiDM。通过完全二值化权重和激活,将扩散模型推向极限的压缩和加速。
概括而言,BiDM目标是解决扩散模型激活特征、模型结构以及生成任务的独特需求,克服完全二值化带来的挑战。
它包含两项创新技术:
从时间角度出发,作者们观察到扩散模型的激活特征与时间步高度相关。
因此引入了“时间步友好二值结构”(TBS),通过可学习的激活二值量化器匹配扩散模型的动态激活范围,并设计跨时间步的特征连接,利用相邻时间步之间的特征相似性,增强二值模型的表示能力。
而从空间角度出发,作者们注意到生成任务中的空间局部性以及扩散模型使用的基于卷积的U-Net结构。
于是提出了“空间分块蒸馏”(SPD),引入一个全精度模型作为监督,通过对分块的自注意模仿,专注于局部特征,更好地引导二值扩散模型的优化方向。
 △具有时间步友好二值结构和空间分块蒸馏的BiDM
△具有时间步友好二值结构和空间分块蒸馏的BiDM
广泛的实验表明,与现有的SOTA完全二值化方法相比,BiDM在保持相同推理效率的同时显著提高了精度,在各种评价指标上超越了所有现有基线方法。
具体来说,在像素空间扩散模型中,BiDM是唯一一种将IS提高到5.18的方法,接近全精度模型的水平,比最佳基线方法高出0.95。
在LDM 中,BiDM将LSUN-Bedrooms的FID从SOTA方法的59.44降低到了令人印象深刻的22.74,同时节省了28.0倍的存储空间和52.7倍的OPs。
作为第一种完全二值化的扩散模型方法,大量生成的样本也证明BiDM是目前唯一一种能够生成可接受的完全二值化DM图像的方法,从而使DM在低资源场景中得到有效应用。
具体咋实现的
二值扩散模型基线
扩散模型:给定一个数据分布𝑥0~𝑞(𝑥0),前向过程生成一个随机变量序列𝑥𝑡 ∊ {𝑥1,…,𝑥𝑇},该序列通过转移核𝑞(𝑥𝑡|𝑥𝑡-1)生成,通常是高斯扰动,其表达式为:

其中𝛽𝑡 ∊(0,1)是噪声调度。高斯转移核允许作者们边缘化联合分布,因此利用𝛼𝑡:=1-𝛽𝑡和 ,可以通过采样一个高斯向量𝜖~N(0,I)并应用变换
,可以通过采样一个高斯向量𝜖~N(0,I)并应用变换 轻松获得𝑥𝑡的样本。
轻松获得𝑥𝑡的样本。
反向过程旨在通过去除噪声生成样本,使用可学习的转移核𝑝𝜃(𝑥𝑡-1|𝑥𝑡)近似不可用的条件分布q(𝑥𝑡-1|𝑥𝑡),其表达式为:
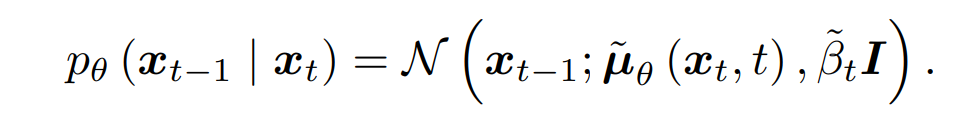
均值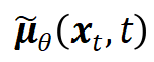 和方差
和方差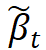 可以使用重参数化技巧得到:
可以使用重参数化技巧得到:
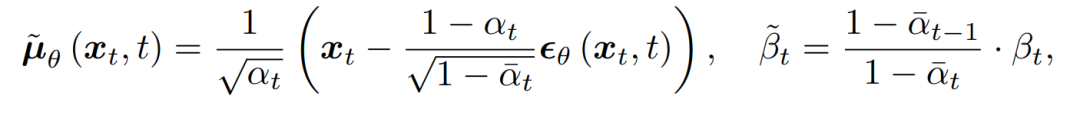
其中𝜖𝜃是具有可学习参数𝜃的函数逼近,用于根据𝑥𝑡预测𝜖。
对于扩散模型的训练,通常使用变分下界的简化变体作为损失函数,以提高样本质量,其表达式为:
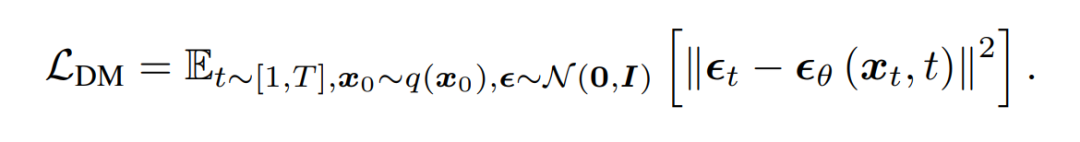
由于 U-Net 能够融合低层次和高维特征,它已成为扩散模型的主流骨干。U-Net 的输入输出块可以表示为 和
和 ,其中较小m对应的块是更低层次的。跳跃连接将低层次信息从Dm(·)传播到Um(·),因此Um接收到的输入表示为:
,其中较小m对应的块是更低层次的。跳跃连接将低层次信息从Dm(·)传播到Um(·),因此Um接收到的输入表示为:

二值化:量化通过将权重和激活离散化为低位宽,压缩并加速噪声估计模型。在二值化扩散模型的基线中,权重W被二值化为1位:

其中符号函数将W限制为+1或-1,并设0为阈值。𝜎是浮点标量,初始化为 (n表示权重数量),并在训练过程中进行学习。
(n表示权重数量),并在训练过程中进行学习。
同时,激活通常通过简单的BNN量化器进行量化:

当权重和激活同时被量化为1位时,去噪模型的计算可以由XNOR和bitcount运算代替,从而实现显著的压缩和加速。
时间步友好二值结构
在详细介绍所提方法之前,作者们先总结对扩散模型(DMs)属性的观察:
下图中, (a) 全精度DDIM模型在CIFAR-10上第4层卷积层的激活范围随去噪步骤变化。(b) 在LSUN-Bedrooms数据集上,全精度LDM-4模型在每一步的输出特征与前一步相似。

观察1:激活范围在长期时间步中变化显著,但激活特征在短期相邻时间步中相似。
之前的研究,如TDQ和Q-DM,已经表明,DMs的激活分布在去噪过程中高度依赖于时间步,表现为相邻时间步之间的相似性,而远距离时间步之间的差异较大,如图2(a)所示。
因此,在所有时间步中应用固定的缩放因子会导致激活范围的严重失真。除了分布范围之外,Deepcache强调了连续时间步之间高维特征的显著时间一致性,如图2(b)所示。
这些现象促使作者们重新审视现有的二值化结构。
二值化,尤其是权重和激活的完全二值化,与4位等低位量化相比,会导致激活范围和精度的更大损失。这使得生成丰富激活特征变得更加困难。激活范围和输出特征的不足严重损害了像DMs这样丰富表示的生成模型。
因此,采用更灵活的激活范围的二值量化器,并通过利用其特征输出来增强模型的整体表达能力,是在完全二值化后提高其生成能力的关键策略。
作者们首先关注长期时间步之间的差异。
大多数现有的激活量化器,如BNN和Bi-Real,直接将激活量化为{+1,-1},如式(7)所示。这种方法严重扰乱了激活特征,负面影响了生成模型的表达能力。一些改进的激活二值量化器,如XNOR++,采用了可训练的缩放因子k:
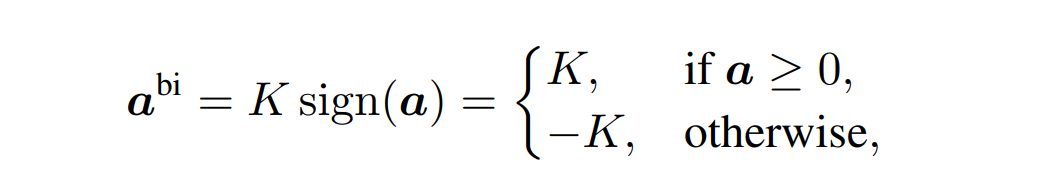
其中K的形式可以是向量或多个向量的乘积,但在推理过程中保持为常量值。尽管这种方法部分恢复了激活的特征表达,但它与高度相关的时间步不匹配,可能仍会导致显著的性能损失。
作者们将注意力转向原始的XNOR,它采用动态计算的均值来构造激活二值量化器。其对二维卷积的运算可以表示为:

其中 ,
, ,
, ,
, 。
。 表示二维过滤器,
表示二维过滤器, 和
和 分别表示带和不带乘法的卷积操作。这种方法自然保留了激活特征的范围,并随着不同时间步的输入范围动态调整。
分别表示带和不带乘法的卷积操作。这种方法自然保留了激活特征的范围,并随着不同时间步的输入范围动态调整。
然而,由于DM特征的丰富表达,局部激活在模块通过前后的范围内表现出不一致,表明预定的k值不能有效恢复激活表示。
因此,作者们使k可调整,并允许其在训练过程中进行学习,以自适应匹配激活在前后发生的范围变化。作者们提出的可学习的微小卷积k的梯度计算过程如下:

值得注意的是,使k可学习不会增加任何额外的推理负担。计算成本保持不变,允许进行高效的二值运算。
另一方面,作者们专注于相邻时间步之间的相似性。
Deepcache直接提取高维特征作为缓存,以跳过U-Net中的大量深度计算,实现了显著的推理加速。其过程表示为:
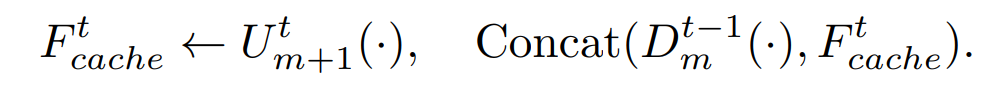
然而,这种方法不适用于二值化扩散模型,因为二值网络的每个输出的信息内容非常有限。对于本质上已经实现了显著压缩和加速但表达能力有限的二值扩散模型,作者们预计相邻时间步之间的特征相似性将增强二值表示,从而弥补表达挑战。
作者们构建了一个跨时间步的信息增强连接,以使用前一时间步的特征丰富当前时间步的表达。其过程可以表示为:

其中 是一个可学习的缩放因子。正如图2(b)所示,不同块和时间步中的高维特征相似性各异。
是一个可学习的缩放因子。正如图2(b)所示,不同块和时间步中的高维特征相似性各异。
因此,作者们设置了多个独立的𝛼值,以允许模型在训练过程中更有效地自适应学习。
总结来说,时间步友好的二值结构(TBS)包括在输入平均和跨时间步连接后应用于缩放因子的可学习微卷积。它们的组合效果能够适应扩散模型在长期时间步中的激活范围变化,并利用相邻时间步之间高维特征的相似性来增强信息表示。
从误差减少的角度来看,图3中展示了TBS的可视化。
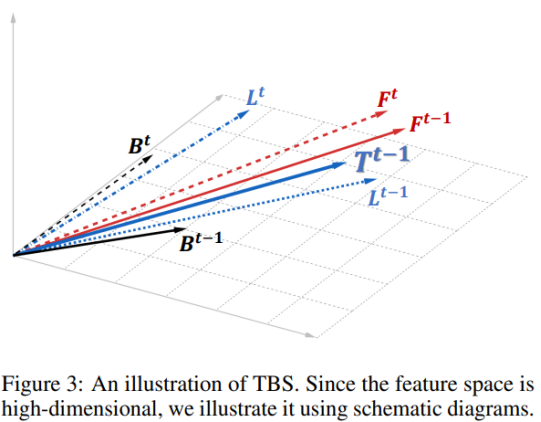
首先,作者们将基线方法下二值扩散模型的输出抽象为向量Bt-1。
缩放因子的不匹配会在它与全精度模型的输出向量Ft-1之间产生显著的长度差异。
通过使用提出的缩放因子和可学习的微卷积,Bt-1被扩展为Lt-1。Lt-1更接近Ft-1,但仍与全精度模型存在方向上的差异。
跨时间步的连接进一步结合了前一个时间步的输出Ft、Bt和Lt。相邻时间步之间的高维特征相似性意味着Ft-1和Ft之间的差距相对较小,从而促进了Lt-1和Lt的结合。
最后,作者们通过应用TBS得到二值化扩散模型的输出,表达式为Tt-1=(1-𝛼)·Lt-1+𝛼·Lt,这一输出最接近全精度模型的输出Ft-1。
空间分块蒸馏
由于生成模型的特性,扩散模型的优化过程与以往的判别模型有着不同的特征:
观察2:传统的蒸馏难以引导完全二值化的扩散模型与全精度模型对齐,而扩散模型在生成任务中的特征在空间上表现出局部性。
在以往的实践中,在量化模型的训练过程中添加蒸馏损失是常见的做法。由于二值模型的数值空间有限,直接使用简单的损失进行优化会导致调整梯度更新方向的困难,使学习变得具有挑战性。因此,向中间特征添加蒸馏损失可以更好地指导模型的局部和全局优化过程。
然而,作为生成模型,扩散模型的高度丰富的特征表示使得二值模型极难细致地模仿全精度模型。
尽管原始扩散模型训练中使用的L2损失与扩散过程中的高斯噪声对齐,但并不适用于中间特征的蒸馏匹配。在常规蒸馏过程中,常用的L2损失往往优先优化差异较大的像素,从而导致更加均匀和平滑的优化结果。
这种全局约束学习过程对于以图像生成为目标的二值模型来说是困难的,因为其有限的表示能力使得精细的蒸馏模仿难以直接调整模型以完全匹配全精度模型的方向。
与此同时,作者们注意到,使用U-Net作为骨干的扩散模型由于其基于卷积的结构和生成任务的要求,天然表现出空间局部性。
这与以往的判别模型不同,判别模型中的任务(如分类)只需整体特征提取,而不需要低层次的要求,这使得传统的蒸馏方法不适用于具有空间局部性的生成任务。此外,大多数现有的扩散模型蒸馏方法专注于减少时间步数,并未解决图像生成任务中对特征空间局部性的需求。
因此,鉴于现有损失函数在优化二值扩散模型上的困难以及扩散模型的空间局部性,作者们提出了空间分块蒸馏(SPD)。
具体来说,他们设计了一种新的损失函数,该损失函数在蒸馏之前将特征划分为小块,然后逐块计算空间自注意力。虽然传统的L2损失使二值扩散模型难以实现直接匹配,导致优化挑战,但注意力机制使得蒸馏优化可以更侧重于关键部分。
然而,对于完全二值化的扩散模型来说,这仍然是具有挑战性的,因为高度离散的二值输出信息有限,使得模型难以捕获全局信息。
因此,作者们通过将中间特征划分为多个小块,并为每个小块独立计算空间自注意力,使得二值模型在优化过程中能够更好地利用局部信息。
SPD首先将二值扩散模型和全精度扩散模型的某个块输出的中间特征𝓕bi和𝓕fp∊𝔽bxcxwxh划分为p2个小块:

然后,分别对每个小块计算自注意力:

在正则化之后,计算并累加相应位置的损失:

其中|| · ||2表示L2函数。最后,总训练损失被计算为:
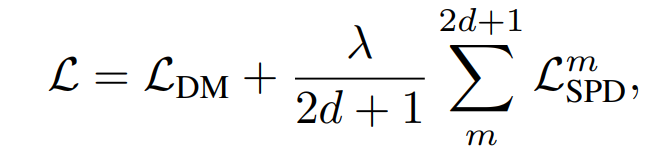
其中,d表示在上采样或下采样过程中块的数量,最终包括中间块在内,共有2d+1中间特征。𝜆是用于平衡损失项的超参数系数,默认为4。
如下图所示,LDM模型在LSUN-bedroom数据集上的最后一个TimeStepBlock输出的可视化。FP32表示全精度模型的输出𝓕fp。Diff表示全精度模型输出与二值化模型输出之间的差异||𝓕fp-𝓕bi||。Ours表示自注意力机制。

作者们对上述提到的中间特征和自注意力进行了可视化。正如图所示,作者们的空间分块蒸馏(SPD)使得模型在每个小块中更加关注局部信息。
实验
作者们在各种数据集上进行了实验,包括CIFAR-10 32×32、LSUN-Bedrooms 256×256、LSUN-Churches 256×256 和FFHQ 256×256,并在像素空间扩散模型和潜在空间扩散模型上进行了测试。
使用的评估指标包括Inception Score (IS)、Fréchet Inception Distance (FID)、Sliding Fréchet Inception Distance (sFID)、精度和召回率。截至目前,还没有研究将扩散模型压缩到如此极端的程度。
因此,作者们使用了经典的二值化算法和最新的最先进的通用二值化算法作为基线。
他们提取了扩散模型中TimestepEmbedBlocks的输出作为TBS和SPD的操作目标。且还在卷积层中采用了与ReActNet相同的快捷连接。详细的实验设置见附录A。
主要结果
像素空间扩散模型:作者们首先在CIFAR-10 32×32数据集上进行了实验。正如表1中所示,使用基线方法对扩散模型进行W1A1二值化导致了显著的性能下降。然而,BiDM在所有指标上均表现出显著改进,实现了前所未有的图像质量恢复。
具体而言,BiDM在IS指标上从4.23提升至5.18,FID指标降低了27.9%。
以下为在CIFAR-10数据集上,使用100步的DDIM二值化结果。

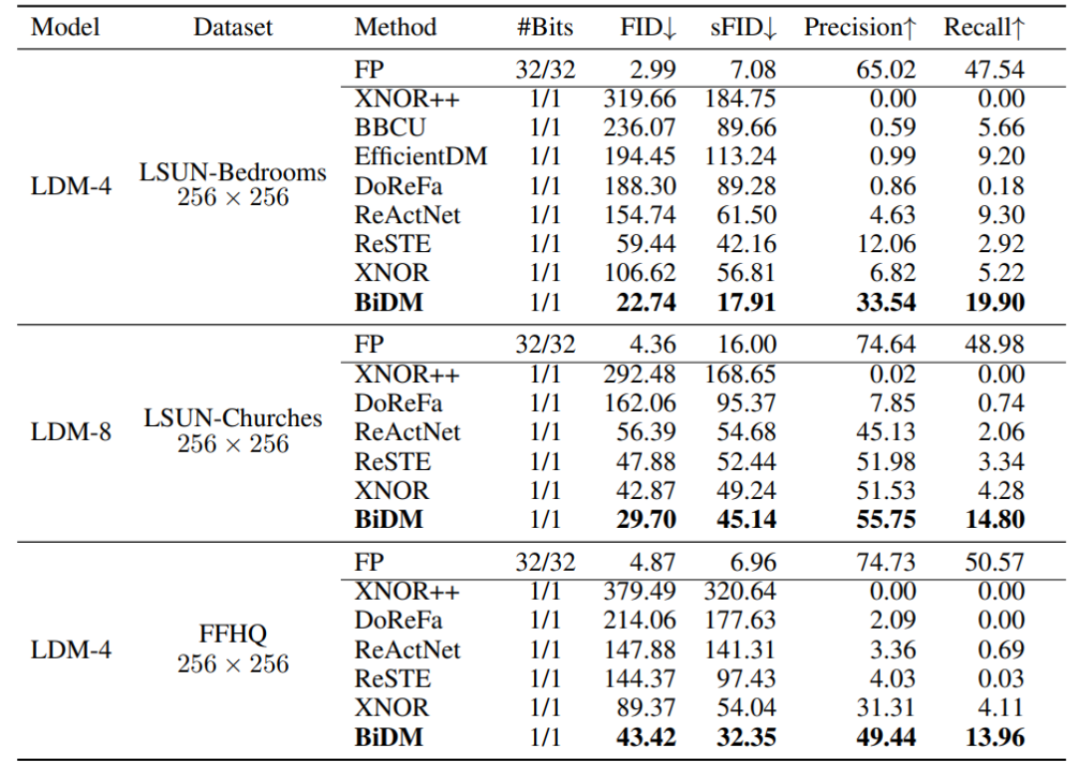
潜在空间扩散模型:作者们的LDM实验包括对LDM-4在LSUN-Bedrooms 256×256和FFHQ 256×256数据集上的评估,以及对LDM-8在LSUN-Churches 256×256数据集上的评估。
实验使用了200步的DDIM采样器,详细结果见表2中。
在这三个数据集中,作者们的方法相对于最好的基线方法取得了显著的改进。与其他二值化算法相比,BiDM在所有指标上都表现优异。
在LSUN-Bedrooms、LSUN-Churches和FFHQ数据集中,BiDM的FID指标分别比基线方法降低了61.7%、30.7%和51.4%。与XNOR++相比,XNOR++在去噪过程中采用了固定的激活缩放因子,导致其激活的动态范围非常有限,使得难以匹配扩散模型高度灵活的生成表示。
BiDM通过使微卷积k可学习,作用于动态计算的缩放因子,解决了这一挑战。这种优化使得各项指标取得了超过一个数量级的显著改进。
在LSUN-Bedrooms和LSUN-Churches数据集中,BiDM的FID指标分别从319.66降低至22.74和从292.48降低至29.70。
此外,与最先进的二值化方法ReSTE相比,BiDM在多个指标上实现了显著提升,特别是在LSUN-Bedrooms数据集中表现出显著的改进。
消融实验
作者们在LSUN-Bedrooms 256×256数据集上对LDM-4进行了全面的消融研究,以评估BiDM中每个提出的组件的有效性。
他们评估了提出的SPD和TBS方法的有效性,结果如表3所示。

当分别将SPD或TBS方法应用于LDM时,相较于原始性能,观察到了显著的改进。当引入TBS方法时,FID和sFID分别从106.62和56.61大幅下降到35.23和25.13。
同样,当添加SPD方法时,FID和sFID分别显著下降到40.62和31.61。其他指标也显示出显著的改善。这证明了作者们的方法在训练过程中通过引入可学习的因子并加入跨时间步的连接,能够持续将二值化模型的特征逼近全精度特征的有效性。
此外,当结合这两种方法并将它们应用于LDM 时,较之单独应用每种方法,观察到额外的改进。这进一步证明了在补丁级别执行全精度和二值模型之间的蒸馏能够显著提高二值模型的性能。
作者们还进行了额外的消融实验,结果在附录B中展示。

效率分析
作者们对模型在完全二值化下的推理效率进行了分析。
表4中的结果表明,BiDM在实现与XNOR基线相同的28.0倍内存效率和52.7倍计算节省的同时,图像生成能力显著优于基线模型,其FID从106.62降低至22.74。

总结
在本文中,作者们提出了BiDM,这是一种全新的完全二值化方法,将扩散模型的压缩推向极限。
基于两个观察——不同时间步的激活特性和图像生成任务的特点,他们分别从时间和空间角度提出了时间步友好的二值结构(TBS) 和 空间分块蒸馏(SPD) 方法。
这些方法解决了完全二值化中表示能力的严重限制,以及高度离散的空间优化挑战。
作为首个完全二值化的扩散模型,BiDM在多个模型和数据集上表现出了显著优于现有最先进通用二值化方法的生成性能。
在LSUN-Bedrooms数据集上,BiDM的FID为22.74,远超最先进方法的FID为59.44,成为唯一能够生成视觉上可接受样本的二值方法,同时实现了高达28.0倍的存储节省和52.7倍的运算效率提升。
更多细节欢迎查阅原论文。
论文链接:
https://arxiv.org/abs/2412.05926
项目主页:
https://github.com/Xingyu-Zheng/BiDM
(文:量子位)
