transformer的encoder编码器进行特征提取本质上就是一个数据建模的过程;
“ 损失函数和梯度下降是神经网络中仅次于神经网络模型本身的两个函数,甚至神经网络模型的性能就是由其所决定的 ”
今天我们来介绍一下神经网络模型中非常重要的两个知识点,损失函数与优化函数。
了解过神经网络模型基础运作流程的应该都知道这两个重要函数,可以说一个神经网络设计的怎么样是一方面,但怎么让神经网络表现更好,就看这两个函数的质量了。
损失函数与优化函数
神经网络训练流程
在现有的神经网络体系中,神经网络的基本运作模式是,根据需求设计完成神经网络结构之后;输入待训练数据,然后神经网络就可以通过损失函数计算模型的拟合误差,然后通过反向传播的方式使用优化函数来优化模型参数,最终达到最优解——可能只是理论最优解不是实际最优解。
基本流程如下图所示:

损失函数
思考一个问题,损失函数的作用是什么?以及它基本理论是什么样的?
从字面来理解,损失函数就是用来计算损失的;但它具体的原理是什么呢?
在神经网络中,数据的基本格式是向量;而向量是有大小和方向的量,因此就可以用向量来表示数据之间的关系——也就是相似度。
以监督学习图像处理为例,给你一堆猫或狗的照片,然后把猫和狗单独放到不同的目录下,也就是猫一个目录,狗一个目录;这时把猫和狗以及他们的标签——也就是目录名称,转化为向量结构之后;表示猫的向量和表示狗的向量会占据不同的向量空间,而表示不同猫的向量会离的近一点;同样表示狗的向量也会离的近一点,这种表示方式就叫做欧式距离。
以生活中的分类问题举例,比如老师在讲台上写两个标签,一个男同学,一个女同学;然后说男同学站男同学标签下,女同学站女同学标签下;
监督学习也是同样的道理,猫狗的标签(目录)就是告诉神经网络模型,这个是猫,那个是狗;然后让神经网络模型自己去根据特征让表示猫的向量和表示狗的向量,尽量靠近猫标签和狗标签。
无监督学习的基础理论和监督学习基本类似,只不过不会告诉神经网络猫和狗的标签;而是让神经网络自己去根据猫狗的特征去区分,虽然区分的结果可能是错的。
但想法虽然很美好,现实却很残酷;未经过训练的神经网络模型就像幼儿园的小孩子一样,虽然你说了,他也听了,但他做的都是错的;但怎么衡量这个错误的大小呢 ?
这就是损失函数的作用,通过计算神经网络给的猫狗向量与真实标签之间的误差,来告诉神经网络你这个搞错了,再想想办法;然后神经网络就会进行新一轮的计算,只不过在从新训练之前会先进行参数调优,也就是优化函数。
数学模型如下图所示:
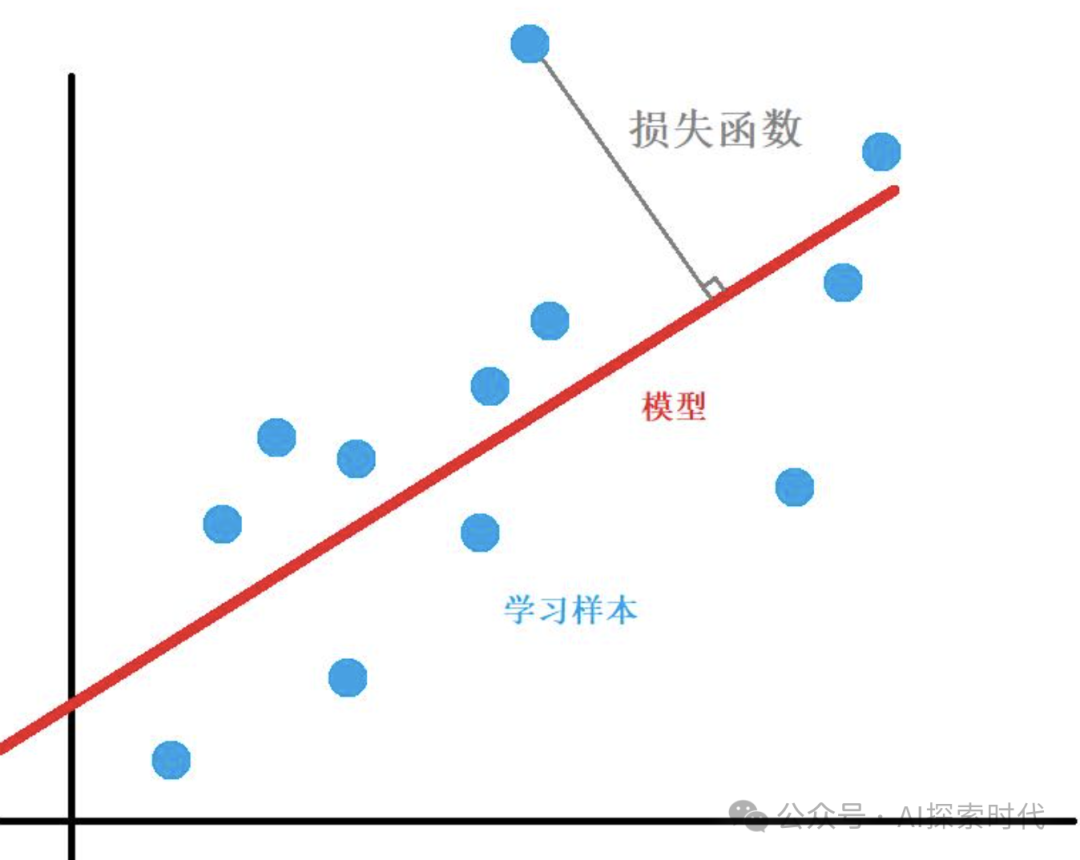
优化函数
优化函数的作用就是告诉神经网络模型,你刚刚算的误差太大了,现在去调整一下你的参数然后从新计算。
但是这里就有一个问题,神经网络怎么知道自己应该怎么调优?总要有一个具体的解决方法或者说算法吧。
这时优化函数的经典实现——梯度下降的作用就体现了;实现优化函数的方式有多种,但使用最多影响力最大的就是梯度下降算法。
什么是梯度下降算法?
想明白什么是梯度下降,首先你要明白什么是梯度;假如某一天你和朋友等山的时候遇到意外伤害,这时你的所有通讯设施都无法使用;必须有一个人下山去通知救援队来救你的队友。这时你需要找一个在保证安全的前提下,能最快下山的路径?这时你应该怎么办?
ok, 先思考一下下山有哪些途径?
1. 找一条人工修好的山路下山,一般是上来的路,也就是原路返回
2. 找一些山间小道,这条路可能会比较难走,但速度会比走修好的山路更快
3. 到悬崖边,直接跳下去,这是下山最快的一种方式,但结果可能就是直接死亡;这时下山就没了意义。
因此,一般情况下大家应该会选择第二种方式下山;因为它能在保证尽量安全的前提下,以最快的速度下山。
但是同样,这样的山路会比第一种的山路要更难走,因为它坡度更大,更陡峭;其实,我们就可以把这个山的坡度理解成梯度。
简单来说,所谓的梯度就是衡量某种事物的变化率,但毕竟梯度只是我们想出来的一个东西;我们需要把梯度构建成一个数学模型,这样我们才能解决它;
而从数学的角度来说梯度其实就是导数问题。导数就是用来衡量函数在某一个点附近的变化率;因此,所谓的梯度问题就是导数问题。只不过真实的神经网络模型中,梯度下降会更复杂,比如与向量相结合,以及偏导数,方向导数等等。
如下图所示:
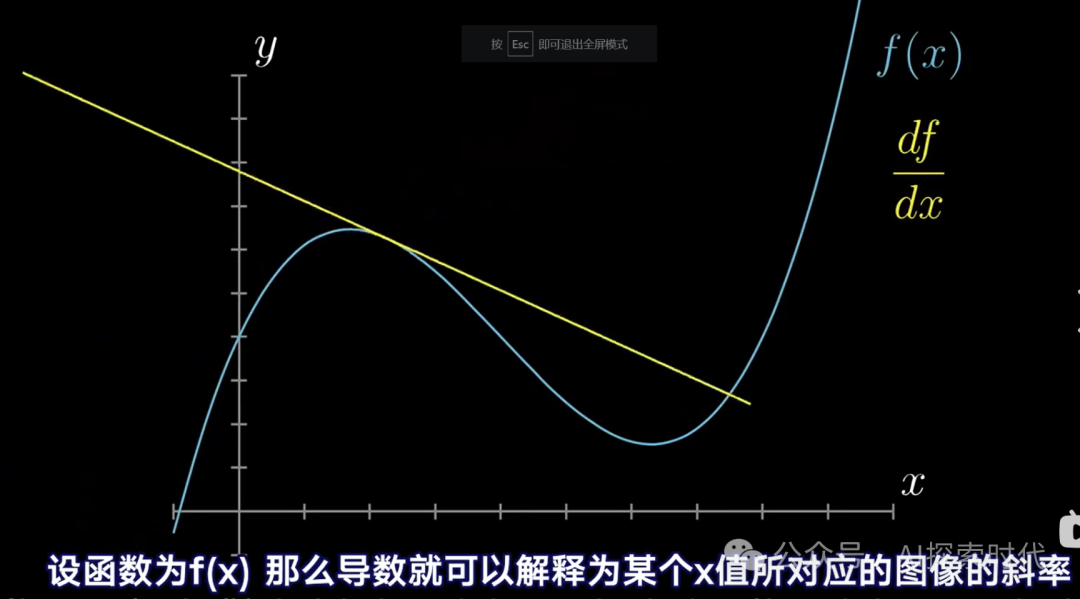
但为什么梯度下降就可以优化损失函数计算的误差?或者说为什么导数就可以解决损失函数的误差?
之所以导数能解决损失函数的误差问题,主要原因就在于,数学追求的一种完美曲线(直线),虽然这个曲线不是一般意义上的水平直线,但它依然是一个连续曲线。
而在数学中,通过导数或者多阶导数就可以求出损失函数在最小值时,自变量x的取值,也就是极值问题。如下图所示,关于导数的求值问题。
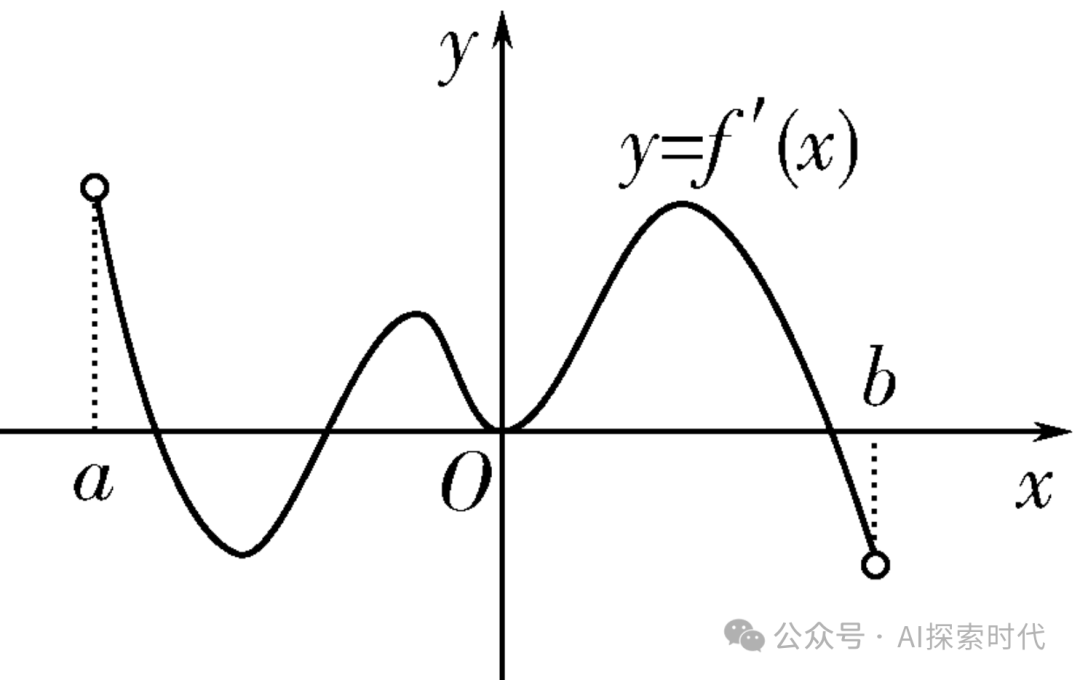
而通过这种方式,损失函数就可以找到其极值点,虽然可能并不是最小值或最大值,原因就在于不同的函数在一定的范围内可能存在多个极值点;这也是为什么前面说,神经网络最终得到的最优解只是理论上的最优解,可能并不是实际上的最优解。
那么现在应该明白为什么优化函数使用梯度下降算法了吧?
原因就在于优化函数会让损失函数在极值点附近不断的去测试,然后找到极值;因为,损失函数不能像我们人类一样,直接画个图看一下极值点在哪里,因此损失函数并不知道其极值点在哪里,只能不断的去计算才能获得结果。
学习率和步长
而关于梯度下降的问题,神经网络还有两个超参数,学习率和步长;步长理解比较简单;以上图导数求极值为例,如果损失函数想求最小值,但它的起始点是a点,但它的最小值点是b点;如果要在a和b之间一个点一个点的实,那么效率也太低了。因此步长就可以调大一点,第一次在a点,第二次就可以跳到第一个极小值点附近,也就是a和o点之间的最低点;第三次到y所在的最高点,第四次就可以到b所在的最小值点。
但从上图也可以看出,如果按照这种步长,损失函数会错过两个极大值和一个极小值点;这就可能会产生梯度消失或者梯度爆炸的问题。步长太大可能会导致梯度消失,而步长太小又可能会导致收敛过慢,训练时间和成本大大增加。
而学习率是直接影响步长的参数,很多时候有些人也会把学习率和步长当作是一个东西。
这也是为什么在模型训练中,需要根据不同的模型和场景设置不同的超参数的原因。
(文:AI探索时代)
