跳至内容
作者|子川
来源|AI先锋官
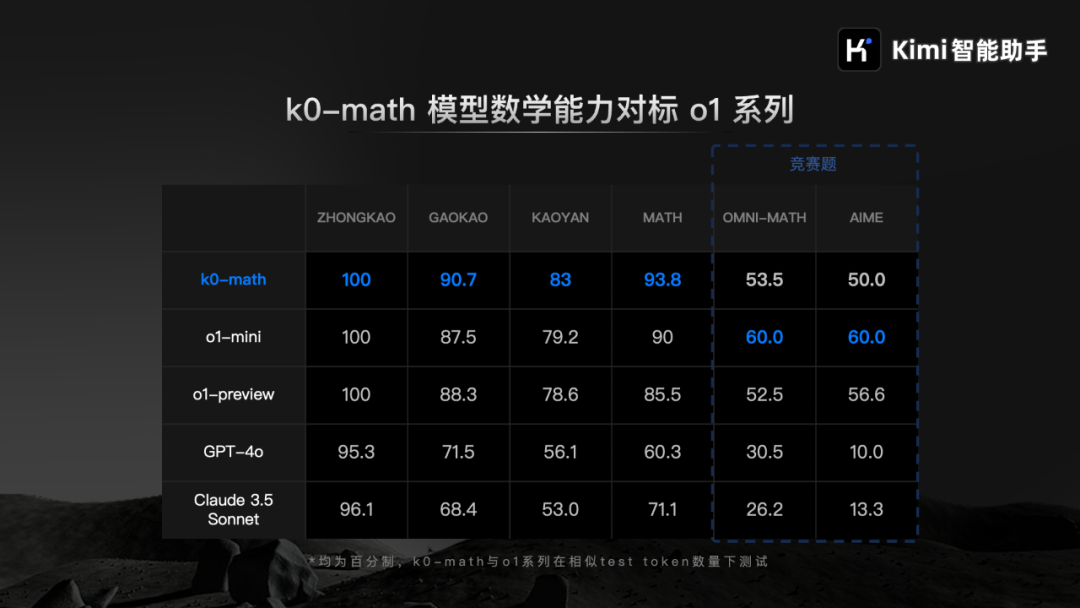
上上周末,Kimi宣布推出它们新一代数学推理模型 k0-math。对标o1,Kimi扔出了一份榜单:
在中考、高考、考研以及包含入门竞赛题的 MATH 等 4 个数学基准测试中,k0-math 初代模型取得的成绩超越 o1-mini 和 o1-preview 模型。延伸阅读:数学推理能力超o1,kimi的数学推理模型它要来了!
k0-math发布后,一直想要进行实测,奈何该模型还处于内部测试阶段。
终于!就在昨天下午,k0-math上线了,打开 Kimi 网页版 kimi.ai,找到侧边栏的「眼镜」图标,就是它了。
随即我们进行了一番实测,用它去体验一下数学竞赛题。
第一题:集合 A={1,2,…,10}的非空子集中,元素和是10的倍数的子集称为好子集.则A的好子集共有多少?
ennnnnnnnnn,可惜,答案是103,从解题过程来看,在102和103之间徘徊,最后根据推理选择了102。
不过可以看到这个计算过程是相当的详细,计算过程的每一步都清晰地写了出来。
小编还发现两个很有意思的点:“反复验证”和“回答通人性”。
起初,k0-math已经给出102这个答案,不过又用另外一种解题思路去验证答案是否准确。
同时计算过程中还会出现着“等等,似乎哪里出错了”“这样就对了”等拟人化的口语,以及计算过程中使用第一人称进行输出。
这种通人性的回答感觉还不错,为枯燥无味的数学解题过程提供了一丝趣味性。毕竟第一人称的优点是能使读者产生一种真实、亲切的感觉,有代入感。
方程 \(5z^4 + 10z^3 + 10z^2 + 5z + 1 = 0\) 有四个复数根,其中模长最大的复数根的实部为多少
第三题:经典大模型数学难题——9.8和9.11谁更大?
在过去不久的双十一,小编为了享受各种优惠,拉了不少朋友凑单。这次也让k0-math来体验凑单的快乐。第四题:
商品A的单价为50元,购买满3件时可享受第4件免费。
商品B的单价为80元,购买满200元即可享受8折优惠。
商品C的单价为100元,购买第2件时可以享受第二件半价,但不能与其他商品组合享受优惠。
小明准备购买以下商品:商品A:6件商品B:3件商品C:2件
在测试过程中,会发现k0-math有两个值得优化的地方:
第一是无法上传图片,毕竟数学领域的图形题占领了数学界的半壁江山。
第二是k0-math目前只支持一轮,不能支持多轮问答,意思就是不能再去追问了。
k0-math新鲜出炉,不少网友和机构也在第一时间进行了测试。
第三方测评机构SuperCLUE,基于SuperCLUE-Math6o奥林匹克数学竞赛基准,对k0-math进行了专项数学能力评估。
测试结果为:与o1-preview相比,数学模型 k0-math 在SC-math6o上仍有18分的差距,排名国内第二,第一的是深度求索的DeepSeek-R1-Lite-Preview。
由于评测的数据集有限,该榜单只能作为参考。不过这也侧面证明:k0-math已经跻身全球数学模型的第一梯队。
目前k0-math模型已经上新到kimi中,感兴趣的同学可以去体验一下。
(文:AI先锋官)