克雷西 发自 凹非寺
量子位 | 公众号 QbitAI
首个FP4精度的大模型训练框架来了,来自微软研究院!
在相同超参数的设置下,可以达到与FP8以及BF16相当的训练效果。
这意味着所需的存储和计算资源可以更少。
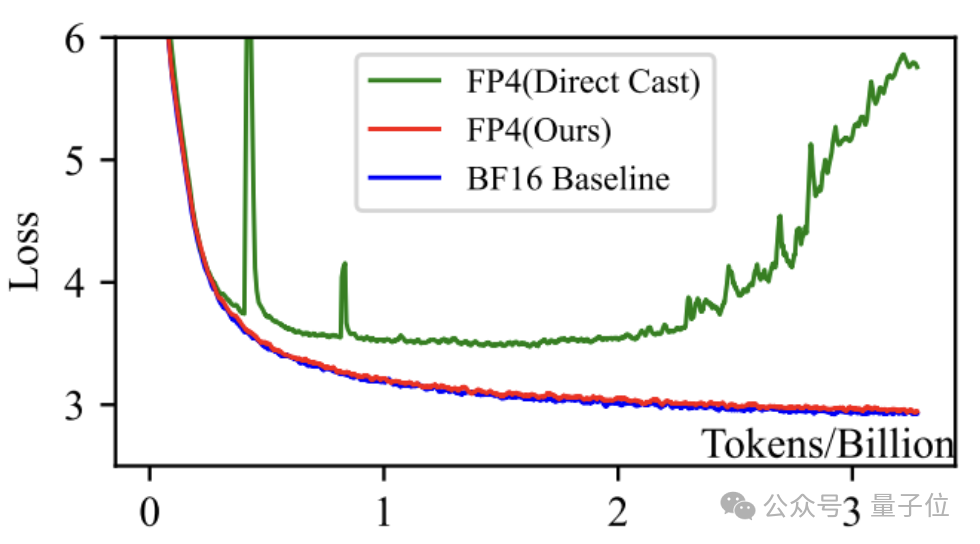
用这种方法训练的模型规模最高可达130亿参数规模,训练Tokens数量也达到千亿级别。
而且用的还不是真·FP4,而是通过FP8来模拟,如果采用真的FP4,效果还能进一步提升。
(注:研究开展时,尚未有原生支持FP4的硬件,故作者通过在FP8的TensorCore上模拟实现)
网友评论说,效率更高质量却没什么损失,FP4真的是个game changer。
还有人说,如果这一发现广为人知,恐怕老黄的股价又要跌了。

当然,因低训练成本而成为当红明星的DeepSeek也被网友cue了一下:

在FP8 TensorCore上模拟FP4
如开头所述,在相同超参数的设置下,作者的方法可以达到与BF16的训练效果。
具体来说,在1.3B、7B和13B的LLaMA模型上,从0到1千万Tokens的训练过程中,作者的FP4训练与BF16的损失曲线基本一致。

在下游任务上,表现同样也和BF16相当。
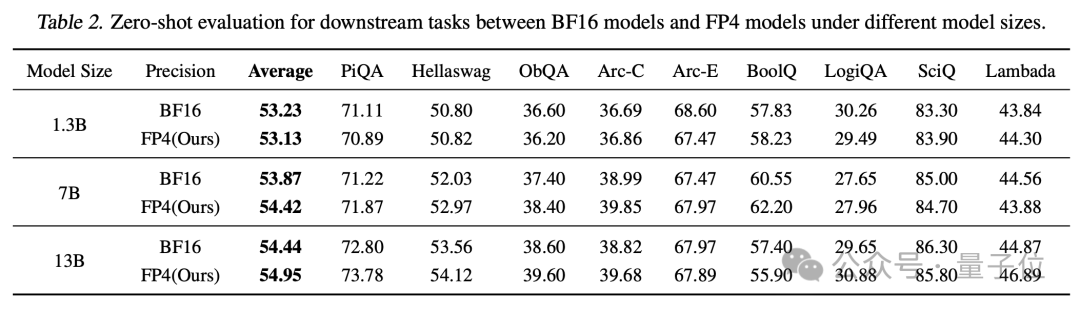
为了实现FP4精度训练,研究团队采用了定制化的FP4矩阵乘法(GeMM)CUDA内核。
在内核中,作者先用FP16将FP4的A和B矩阵读入共享内存并做相应变换,然后用FP4完成分块矩阵乘法,最后再用FP16对中间结果进行归约,得到FP16格式的输出矩阵。
首先需要确定量化的数据格式,该框架采用了E2M1的FP4格式,即用2位来表示指数,1位表示尾数,外加1位符号位,总共4位。
选择这个格式是为了契合当前主流ML加速芯片的量化计算单元设计。
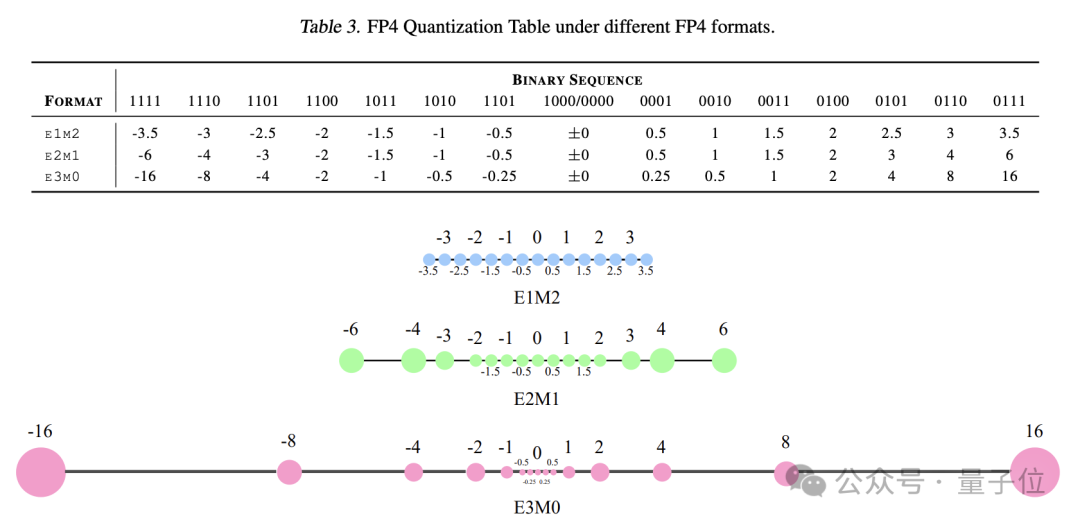
并且,这个框架对权重矩阵W和激活矩阵A采取了不同粒度的量化策略。
对W做的是列方向(channel-wise)的量化,而对A做的是行方向(token-wise)的量化。
这种量化粒度是与GeMM在硬件上的并行实现方式相契合的,可以在不引入额外矩阵转置操作的前提下,最大化发挥FP4在矩阵乘法上的加速效果。
在模型前向传播开始时,框架对每一个线性层的权重矩阵W和输入激活矩阵A同时进行FP4量化。
量化时,先对矩阵中的数值进行缩放和偏移,将其映射到FP4所能表示的范围内,然后通过查表的方式将其四舍五入到最近的FP4离散值。
由于不同层的数值范围差异很大,所以需要对每一层的权重矩阵和激活矩阵分别确定一个独立的量化范围,即进行逐层的量化参数校准。
这个框架采用的是scale+shift的校准方法,即先用一个缩放因子将数值从原始范围映射到[-1,1],再用一个偏移因子把[-1,1]平移到FP4所能表示的范围。
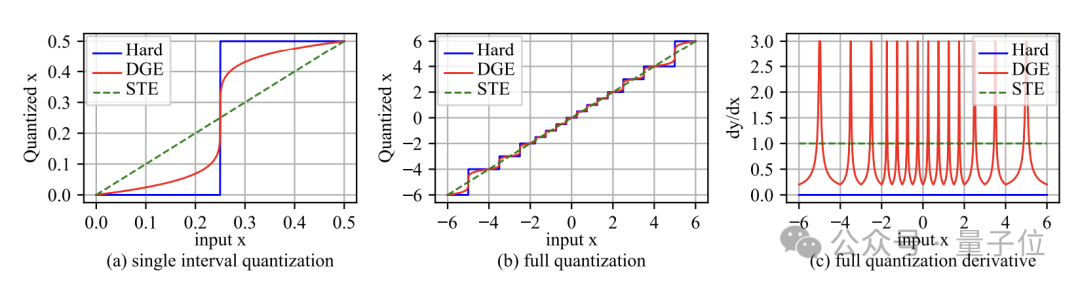
在反向传播过程中,如果直接对量化后的矩阵求导,则权重矩阵的梯度几乎处处为0,从而无法进行参数更新。
为此,作者提出了一种新颖的可微分梯度估计方法。
它在前向计算时仍然使用硬量化,以保证计算效率,但在反向传播时,用一个连续可微的函数来重新拟合这个量化函数,并求导得到一个对梯度的修正项。
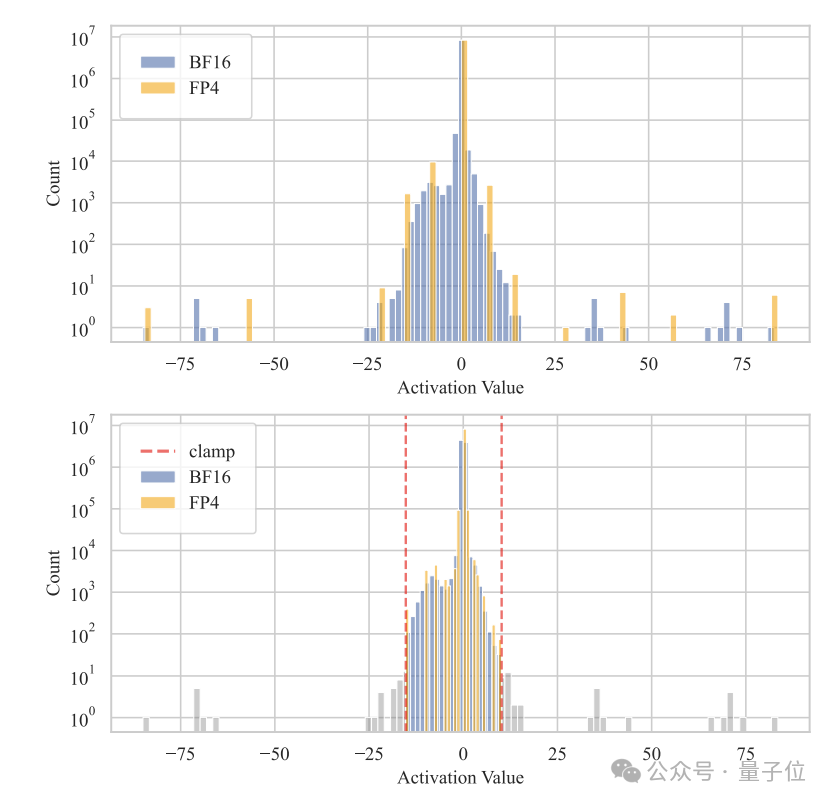
另外在训练过程中,模型的隐层激活分布通常呈现出明显的长尾特征,少数维度上的数值明显偏大,导致出现“离群点”(outlier)。
针对这个问题,作者提出了一种“离群点削峰和补偿”的策略。
具体来说,先在激活矩阵A中,通过分位数检索的方法找出那些幅值最大的离群点,将它们限幅到某一个预设的阈值范围内,得到削峰后的矩阵A_clamped。
然后,再基于原矩阵A和削峰后的A_clamped,构造出一个稀疏补偿矩阵∆A,其中只有那些被削峰的位置是非零的。
此外在部分环节当中,作者还采用了混合精度设计。
比如在梯度通信时采用了FP8,在优化器状态(如动量)的存储时选择了FP16。在系统的其他部分,如非矩阵乘操作的计算、Loss Scaling等,也都采用了FP16。
通过这些混合精度的设计,在保证训练数值稳定性的前提下,尽可能地降低了计算和存储开销。
中科大博士生一作
这个框架由微软亚洲研究院和SIGMA团队打造,所有研究人员都是华人。
第一作者Ruizhe Wang是中科大在读博士生,目前在MSRA实习,研究方向就包括低精度量化。
中科大科研部部长、类脑智能国家工程实验室执行主任、博士生导师查正军教授也参与了这一项目。
通讯作者为MSRA高级首席研究经理(Senior Principal Research Manager)程鹏和首席研究经理(Principal Research Manager)Yeyun Gong。
程鹏曾先后就读于北航和清华,在清华读博期间还到UCLA访问学习;Yeyun Gong则是复旦博士,毕业后即加入微软。
MSRA杰出科学家、常务副院长郭百宁也参与了本项目,他先后就读于北大和康奈尔大学,1999年就已加入微软。
此外还有其他作者,完整名单如下:

论文地址:
https://arxiv.org/abs/2501.17116
(文:量子位)

