0x0. 前言
今天介绍一个在SGLang中针对DeepSeek V3模型中的 https://github.com/sgl-project/sglang/blob/main/python/sglang/srt/layers/moe/topk.py#L99-L149 部分的 biased_grouped_topk 函数的kernel优化,在DeepSeek V3端到端测试中吞吐提升5%以上。这个函数用于DeepSeek V3/R1模型中的MOE层,用于计算每个token的专家选择概率。相比于Mixtral,Qwen2等MoE模型的topk实现,DeepSeek V3引入了grouped_topk的机制,让每个token只能选择固定数量的专家组,然后每个专家组内再选择topk个专家。下面是这个函数的注释:
# 输入张量维度说明:
# hidden_states: [num_token, ...] # 具体其他维度取决于模型架构
# gating_output: [num_token, num_experts] # num_experts必须能被num_expert_group整除
# correction_bias: [num_experts] # 用于修正门控输出的偏置项
# 其中:
# - num_token: 批次中的token数量
# - num_experts: 专家总数,必须能被num_expert_group整除
# - num_expert_group: 专家组的数量
# - topk: 每个token要选择的专家数量
# - topk_group: 每个token要选择的专家组数量
# 约束条件:
# - topk_group <= num_expert_group
# - topk <= num_experts
# - num_experts % num_expert_group == 0
def biased_grouped_topk_impl(
hidden_states: torch.Tensor, # 输入的隐藏状态张量
gating_output: torch.Tensor, # 门控网络的输出,用于计算专家选择概率
correction_bias: torch.Tensor, # 用于修正门控输出的偏置项
topk: int, # 每个token选择的专家数量
renormalize: bool, # 是否对选择的专家权重进行重新归一化
num_expert_group: int = 0, # 专家组的数量
topk_group: int = 0, # 每个token选择的专家组数量
):
# 确保输入token数量匹配
assert hidden_states.shape[0] == gating_output.shape[0], "Number of tokens mismatch"
# 对门控输出进行sigmoid激活,得到专家选择概率
scores = gating_output.sigmoid()
num_token = scores.shape[0] # 获取token数量
num_experts = scores.shape[1] # 获取专家总数
# 将scores重塑并添加修正偏置
scores_for_choice = scores.view(num_token, -1) + correction_bias.unsqueeze(0)
# 计算每个专家组的得分:
# 1. 将scores重塑为[num_token, num_expert_group, experts_per_group]
# 2. 在每个组内选择top2的得分
# 3. 对每个组的top2得分求和,得到组得分
group_scores = (
scores_for_choice.view(num_token, num_expert_group, -1)
.topk(2, dim=-1)[0]
.sum(dim=-1)
) # [n, n_group]
# 选择得分最高的topk_group个专家组
group_idx = torch.topk(group_scores, k=topk_group, dim=-1, sorted=False)[1] # [n, top_k_group]
# 创建组掩码,标记被选中的组
group_mask = torch.zeros_like(group_scores) # [n, n_group]
group_mask.scatter_(1, group_idx, 1) # [n, n_group]
# 扩展组掩码到专家级别
score_mask = (
group_mask.unsqueeze(-1)
.expand(num_token, num_expert_group, scores.shape[-1] // num_expert_group)
.reshape(num_token, -1)
) # [n, e]
# 将未选中组的专家得分设为负无穷
tmp_scores = scores_for_choice.masked_fill(
~score_mask.bool(), float("-inf")
) # [n, e]
# 在选中的专家组中选择topk个专家
_, topk_ids = torch.topk(tmp_scores, k=topk, dim=-1, sorted=False)
# 获取选中专家的原始得分作为权重
topk_weights = scores.gather(1, topk_ids)
# 如果需要重新归一化,对选中的专家权重进行归一化处理
if renormalize:
topk_weights_sum = topk_weights.sum(dim=-1, keepdim=True)
topk_weights = topk_weights / topk_weights_sum
# 返回归一化后的权重和选中的专家ID
return topk_weights.to(torch.float32), topk_ids.to(torch.int32)
无论是vLLM还是SGLang都是通过torch.compile来对这个函数进行优化,使用torch.compile的明显劣势就是启动服务的时间大大延长了,并且torch.compile优化后的性能相比于手动用CUDA实现还是有一定的差距,因为涉及到topk和gather这种复杂的算子,并不能对这个算子做完全的fuse 。本篇博客将介绍一下 SGLang 中针对这个函数的CUDA kernel fuse实现,PR为:https://github.com/sgl-project/sglang/pull/4530 。
0x1. 性能测试
kernel PR的测试 (https://github.com/sgl-project/sglang/pull/4530)
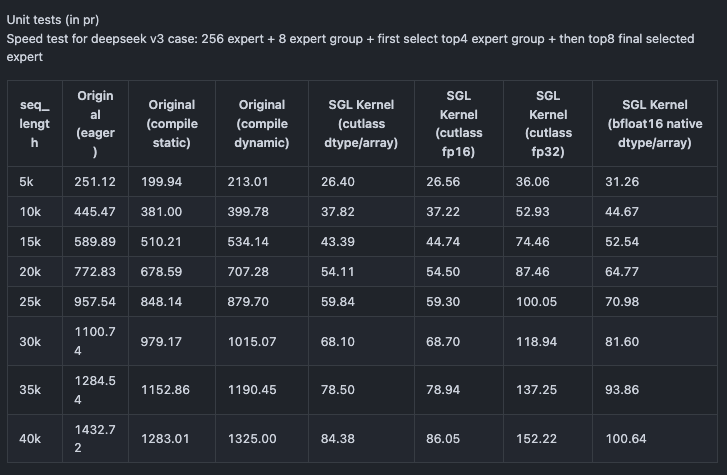
这里的seq_length就是上面的num_tokens,假设bs=1。从这里的结果来看,在不同的token数下,CUDA kernel fuse后的性能相比于torch.compile的版本都有数量级的领先。
下面的测试来自:https://github.com/sgl-project/sglang/pull/5371
torch profile
python3 -m sglang.bench_serving --backend sglang --num-prompts 2 --request-rate 1 --port 30001 --flush-cache --warmup-requests 1 --profile
主分支

替换moe_fused_gate kernel后的分支

现在只有一个kernel了。
36us->8us.
替换moe_fused_gate kernel后的DeepSeek V3模型H200端到端测试
SGL_ENABLE_JIT_DEEPGEMM=0 python3 -m sglang.launch_server --model /DeepSeek-V3 --tp 8 --trust-remote-code --port 30001
python3 -m sglang.bench_serving --backend sglang --num-prompts 300 --request-rate 1 --port 30001 --flush-cache --warmup-requests 20
|
|
|
|
|
|---|---|---|---|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-
qps=4: 5.9%+ -
qps=8: 5.5%+ -
qps=16: 8.1%+
0x2. moe_fused_gate kernel 走读
代码链接:https://github.com/sgl-project/sglang/blob/main/sgl-kernel/csrc/moe/moe_fused_gate.cu
0x2.1 Host端代码和线程模型
//------------------------------------------------------------------------------
// Host端启动函数
//------------------------------------------------------------------------------
std::vector<at::Tensor>
moe_fused_gate(at::Tensor& input, at::Tensor& bias, int64_t num_expert_group, int64_t topk_group, int64_t topk) {
// 获取输入张量的维度信息
int64_t num_rows = input.size(0); // token数量
int32_t num_experts = input.size(1); // 专家总数
// 创建输出张量,用于存储权重和索引
auto options = torch::TensorOptions().dtype(torch::kFloat32).device(torch::kCUDA);
auto output = torch::empty({num_rows, topk}, options); // 存储选中的专家权重
auto indices = torch::empty({num_rows, topk}, options.dtype(torch::kInt32)); // 存储选中的专家索引
// 根据num_expert_group计算网格维度
// 每个warp处理的行数 = max(WARP_SIZE / num_expert_group, 1)
int64_t rows_per_warp = std::max<int64_t>(1, WARP_SIZE / num_expert_group);
int64_t num_warps = (num_rows + rows_per_warp - 1) / rows_per_warp; // 需要的warp数量
int64_t num_blocks = (num_warps + WARPS_PER_CTA - 1) / WARPS_PER_CTA; // 需要的block数量
// 获取当前CUDA流
const cudaStream_t stream = at::cuda::getCurrentCUDAStream();
// 设置block维度:每个block包含WARPS_PER_CTA * WARP_SIZE个线程,WARPS_PER_CTA个warp
dim3 block_dim(WARP_SIZE, WARPS_PER_CTA);
// 检查1:确保专家数量是2的幂
TORCH_CHECK((num_experts & (num_experts - 1)) == 0, "num_experts must be a power of 2, but got ", num_experts);
// 检查2:确保专家数量能被专家组数量整除(这也意味着专家组数量必须是2的幂)
TORCH_CHECK(
num_experts % num_expert_group == 0,
"num_experts must be divisible by num_expert_group, but got ",
num_experts,
" / ",
num_expert_group);
// 计算每个组内的专家数量
int computed_vpt = num_experts / num_expert_group;
// 检查3:确保每个组内的专家数量不超过MAX_VPT=32
// MAX_VPT表示每个线程能处理的最大值
TORCH_CHECK(
computed_vpt <= MAX_VPT,
"Per group experts: num_experts / num_expert_group = (",
computed_vpt,
") exceeds the maximum supported (",
MAX_VPT,
")");
// 根据已知的编译时配置分发到模板化的kernel
// 目前仅支持以下情况:
// 情况1:256个专家,8或16个组
// 情况2:128个专家,4或8个组
// 情况3:其他情况,要求8 <= num_experts / num_expert_group <= 32
bool dispatched = false;
switch (num_experts) {
case256:
if (num_expert_group == 8)
// DeepSeek V3的情况
// VPT = 256/8 = 32, ROWS_PER_WARP = 32/8 = 4, ROWS_PER_CTA = 6 * 4 = 24
if (input.scalar_type() == at::kBFloat16) {
LAUNCH_MOE_GATE_CONFIG(bfloat16_t, 256, 8);
} elseif (input.scalar_type() == at::kHalf) {
LAUNCH_MOE_GATE_CONFIG(float16_t, 256, 8);
} elseif (input.scalar_type() == at::kFloat) {
LAUNCH_MOE_GATE_CONFIG(float32_t, 256, 8);
} elseif (num_expert_group == 16)
// VPT = 256/16 = 16, ROWS_PER_WARP = 32/16 = 2, ROWS_PER_CTA = 6 * 2 = 12
if (input.scalar_type() == at::kBFloat16) {
LAUNCH_MOE_GATE_CONFIG(bfloat16_t, 256, 16);
} elseif (input.scalar_type() == at::kHalf) {
LAUNCH_MOE_GATE_CONFIG(float16_t, 256, 16);
} elseif (input.scalar_type() == at::kFloat) {
LAUNCH_MOE_GATE_CONFIG(float32_t, 256, 16);
}
break;
case128:
if (num_expert_group == 4)
// VPT = 128/4 = 32, ROWS_PER_WARP = 32/16 = 2, ROWS_PER_CTA = 6 * 2 = 12
if (input.scalar_type() == at::kBFloat16) {
LAUNCH_MOE_GATE_CONFIG(bfloat16_t, 128, 4);
} elseif (input.scalar_type() == at::kHalf) {
LAUNCH_MOE_GATE_CONFIG(float16_t, 128, 4);
} elseif (input.scalar_type() == at::kFloat) {
LAUNCH_MOE_GATE_CONFIG(float32_t, 128, 4);
} elseif (num_expert_group == 8)
// VPT = 128/8 = 16, ROWS_PER_WARP = 32/8 = 4, ROWS_PER_CTA = 6 * 4 = 24
if (input.scalar_type() == at::kBFloat16) {
LAUNCH_MOE_GATE_CONFIG(bfloat16_t, 128, 8);
} elseif (input.scalar_type() == at::kHalf) {
LAUNCH_MOE_GATE_CONFIG(float16_t, 128, 8);
} elseif (input.scalar_type() == at::kFloat) {
LAUNCH_MOE_GATE_CONFIG(float32_t, 128, 8);
}
break;
default:
break;
}
// 如果没有匹配到预定义的配置,使用动态kernel
// 目前动态kernel仅支持num_experts / num_expert_group <= 32的情况
if (!dispatched) {
if (input.scalar_type() == at::kBFloat16) {
moe_fused_gate_kernel_dynamic<bfloat16_t><<<num_blocks, block_dim, 0, stream>>>(
input.data_ptr(),
bias.data_ptr(),
output.data_ptr<float>(),
indices.data_ptr<int32_t>(),
num_rows,
num_experts,
num_expert_group,
topk_group,
topk);
} elseif (input.scalar_type() == at::kHalf) {
moe_fused_gate_kernel_dynamic<float16_t><<<num_blocks, block_dim, 0, stream>>>(
input.data_ptr(),
bias.data_ptr(),
output.data_ptr<float>(),
indices.data_ptr<int32_t>(),
num_rows,
num_experts,
num_expert_group,
topk_group,
topk);
} elseif (input.scalar_type() == at::kFloat) {
moe_fused_gate_kernel_dynamic<float32_t><<<num_blocks, block_dim, 0, stream>>>(
input.data_ptr(),
bias.data_ptr(),
output.data_ptr<float>(),
indices.data_ptr<int32_t>(),
num_rows,
num_experts,
num_expert_group,
topk_group,
topk);
} else {
TORCH_CHECK(false, "Unsupported data type for moe_fused_gate");
}
}
return {output, indices};
}
根据Host端的代码以及kernel开头定义的注释,我们可以画出来线程模型。
static constexpr int WARP_SIZE = 32; // 每个warp固定32个线程
static constexpr int WARPS_PER_CTA = 6; // 每个block有6个warp
dim3 block_dim(WARP_SIZE, WARPS_PER_CTA); // block维度为(32, 6)
int64_t rows_per_warp = std::max<int64_t>(1, WARP_SIZE / num_expert_group); // 每个warp处理的行数
int64_t num_warps = (num_rows + rows_per_warp - 1) / rows_per_warp; // 总共需要的warp数
int64_t num_blocks = (num_warps + WARPS_PER_CTA - 1) / WARPS_PER_CTA; // 需要的block数
线程模型表示为:
Grid结构:
+------------------------+
| Block 0 Block 1 |
| +------+ +------+ |
| | | | | |
| | | | | | ... 更多Block
| | | | | | (num_blocks个Block)
| +------+ +------+ |
| |
+------------------------+
Block结构(dim3(32,6)):
+--------------------------------+
| Warp 0 (32个线程) |
| +----------------------------+ |
| |t0 t1 t2 ... t31 | |
| +----------------------------+ |
| Warp 1 |
| +----------------------------+ |
| |t32 t33 t34 ... t63 | |
| +----------------------------+ |
| ... |
| Warp 5 |
| +----------------------------+ |
| |t160 t161 ... t191 | |
| +----------------------------+ |
+--------------------------------+
数据处理映射:
- 每个Block处理 ROWS_PER_CTA = WARPS_PER_CTA * ROWS_PER_WARP 行数据
- 每个Warp处理 ROWS_PER_WARP = WARP_SIZE/num_expert_group 行数据
- 每个线程处理 VPT = num_experts/num_expert_group 个专家(每个线程处理一个group里面的experts_per_group个专家)
以DeepSeek V3为例(num_experts=256, num_expert_group=8):
-
VPT = 256/8 = 32:每个线程处理32个专家 -
ROWS_PER_WARP = 32/8 = 4:每个warp处理4行数据 -
ROWS_PER_CTA = 6 * 4 = 24:每个block处理24行数据
0x2.2 dispatch 的2种 kernel 接口
//------------------------------------------------------------------------------
// 模板化Kernel版本(使用编译时常量)
//------------------------------------------------------------------------------
// 定义kernel参数结构体,所有参数都是编译时常量
template <int VPT_, int NUM_EXPERTS_, int THREADS_PER_ROW_, int ROWS_PER_WARP_, int ROWS_PER_CTA_, int WARPS_PER_CTA_>
struct KernelParams {
staticconstexprint VPT = VPT_; // 每个线程处理的专家数量(Values Per Thread)
staticconstexprint NUM_EXPERTS = NUM_EXPERTS_; // 总专家数量
staticconstexprint THREADS_PER_ROW = THREADS_PER_ROW_; // 处理每行数据需要的线程数,等于专家组数量
staticconstexprint ROWS_PER_WARP = ROWS_PER_WARP_; // 每个warp处理的行数
staticconstexprint ROWS_PER_CTA = ROWS_PER_CTA_; // 每个CTA(block)处理的行数
staticconstexprint WARPS_PER_CTA = WARPS_PER_CTA_; // 每个CTA包含的warp数量
};
// 模板化的kernel函数定义
template <
typename T, // 数据类型(float/half/bfloat16)
int VPT, // 每线程处理的专家数
int NUM_EXPERTS, // 总专家数
int THREADS_PER_ROW, // 每行需要的线程数
int ROWS_PER_WARP, // 每warp处理的行数
int ROWS_PER_CTA, // 每block处理的行数
int WARPS_PER_CTA> // 每block的warp数
__global__ void moe_fused_gate_kernel(
void* input, // 输入张量
void* bias, // 偏置张量
float* output_ptr, // 输出权重
int32_t* indices_ptr,// 输出专家索引
int64_t num_rows, // 总行数(token数量)
int64_t topk_group, // 每个token选择的专家组数量
int64_t topk) { // 每个token选择的专家数量
// 构造编译时参数结构体
KernelParams<VPT, NUM_EXPERTS, THREADS_PER_ROW, ROWS_PER_WARP, ROWS_PER_CTA, WARPS_PER_CTA> params;
// 调用实现函数
moe_fused_gate_impl<T>(input, bias, output_ptr, indices_ptr, num_rows, topk_group, topk, params);
}
// 用于启动kernel的宏,计算编译时常量并启动kernel
#define LAUNCH_MOE_GATE_CONFIG(T, EXPERTS, EXPERT_GROUP) \
do { \
// 计算每个线程处理的专家数量
constexprint VPT = (EXPERTS) / (EXPERT_GROUP); \
// 如果专家组数量大于WARP_SIZE,每个warp只处理1行,否则计算每个warp可以处理的行数
constexprint ROWS_PER_WARP = ((EXPERT_GROUP) <= WARP_SIZE) ? (WARP_SIZE / (EXPERT_GROUP)) : 1; \
// 计算每个block可以处理的总行数
constexprint ROWS_PER_CTA = WARPS_PER_CTA * ROWS_PER_WARP; \
// 启动kernel
moe_fused_gate_kernel<T, VPT, (EXPERTS), (EXPERT_GROUP), ROWS_PER_WARP, ROWS_PER_CTA, WARPS_PER_CTA> \
<<<num_blocks, block_dim, 0, stream>>>( \
input.data_ptr(), \
bias.data_ptr(), \
output.data_ptr<float>(), \
indices.data_ptr<int32_t>(), \
num_rows, \
topk_group, \
topk); \
dispatched = true; \
} while (0)
//------------------------------------------------------------------------------
// 动态Kernel版本(运行时计算参数)
//------------------------------------------------------------------------------
// 运行时参数结构体
struct KernelParamsDynamic {
int VPT; // 每线程处理的专家数
int NUM_EXPERTS; // 总专家数
int THREADS_PER_ROW; // 每行需要的线程数
int ROWS_PER_WARP; // 每warp处理的行数
int ROWS_PER_CTA; // 每block处理的行数
int WARPS_PER_CTA; // 每block的warp数
};
// 动态参数版本的kernel函数
template <typename T>
__global__ void moe_fused_gate_kernel_dynamic(
void* input,
void* bias,
float* output_ptr,
int32_t* indices_ptr,
int64_t num_rows,
int64_t num_experts, // 运行时指定的专家数量
int64_t num_expert_group, // 运行时指定的专家组数量
int64_t topk_group,
int64_t topk) {
KernelParamsDynamic params;
// 运行时计算所有参数
params.NUM_EXPERTS = num_experts; // 例如:deepseek v3中是256
params.VPT = num_experts / num_expert_group; // 例如:deepseek v3中是256/8=32
params.THREADS_PER_ROW = num_expert_group; // 固定为专家组数量,例如:deepseek v3中是8
params.WARPS_PER_CTA = WARPS_PER_CTA; // 固定为6
params.ROWS_PER_WARP = std::max<int64_t>(1, WARP_SIZE / num_expert_group); // WARP_SIZE固定为32
params.ROWS_PER_CTA = params.WARPS_PER_CTA * params.ROWS_PER_WARP;
// 调用实现函数
moe_fused_gate_impl<T>(input, bias, output_ptr, indices_ptr, num_rows, topk_group, topk, params);
}
这里有2个kernel,一个是模板化的kernel,一个是动态的kernel。模板化的kernel在编译时会计算所有参数,然后启动kernel。动态的kernel在运行时计算所有参数,然后启动kernel。但2个kernel都遵循上一节介绍的线程模型,即每个线程处理固定数量的专家(VPT),多个线程组成一个组来处理一行数据(THREADS_PER_ROW),多个线程组构成一个warp,多个warp构成一个block(CTA)。
0x2.3 辅助函数和数据结构
// 使用CUTLASS库的AlignedArray作为对齐数组的基础类型
template <typename T, int N>
using AlignedArray = cutlass::AlignedArray<T, N>;
// 定义常用数据类型别名
usingbfloat16_t = cutlass::bfloat16_t; // brain floating point 16位
usingfloat16_t = cutlass::half_t; // IEEE 754 half precision 16位
usingfloat32_t = float; // 标准32位浮点数
// 比较函数:处理不同数据类型的大于操作
// 特别处理at::Half类型,因为它的运算符重载会导致歧义
template <typename T>
__device__ inline bool cmp_gt(const T& a, const T& b) {
if constexpr (std::is_same<T, at::Half>::value) {
// 对于at::Half类型,先转换为float再比较,避免运算符重载歧义
returnstatic_cast<float>(a) > static_cast<float>(b);
} else {
// 对于其他类型(float, BFloat16, half_t等),直接使用内置的>运算符
return a > b;
}
}
// 比较函数:处理不同数据类型的相等操作
template <typename T>
__device__ inline bool cmp_eq(const T& a, const T& b) {
if constexpr (std::is_same<T, at::Half>::value) {
// 对于at::Half类型,转换为float再比较
returnstatic_cast<float>(a) == static_cast<float>(b);
} else {
// 其他类型直接使用==运算符
return a == b;
}
}
// 定义所有kernel共用的固定常量
staticconstexprint WARP_SIZE = 32; // CUDA warp大小,固定为32个线程
staticconstexprint WARPS_PER_CTA = 6; // 每个CTA(block)包含6个warp
staticconstexprint MAX_VPT = 32; // 每个线程最多处理32个专家值
// 必须大于 params.VPT(num_expert/num_expert_group)
// 创建Array类型别名,使用AlignedArray确保内存对齐
template <typename T, int N>
using Array = AlignedArray<T, N>;
// 定义访问类型,用于向量化加载数据
// 注意:这里的MAX_VPT必须是编译时常量,且要大于实际的params.VPT值
template <typename T>
using AccessType = AlignedArray<T, MAX_VPT>;
这段代码主要完成了数据类型的定义和我们在Host端启动kernel时需要用到的常量定义以及两个比较函数用于kernel中的topk操作。
0x2.4 moe_fused_gate_impl cuda kernel具体实现
初始化和数据加载
int tidx = threadIdx.x;
int64_t thread_row =
blockIdx.x * params.ROWS_PER_CTA + threadIdx.y * params.ROWS_PER_WARP + tidx / params.THREADS_PER_ROW;
if (thread_row >= num_rows) {
return;
}
这部分计算每个线程处理的行(token)索引。其中:
-
thread_row对应Python代码中的token索引,用于访问hidden_states[token_idx]和gating_output[token_idx] -
params.THREADS_PER_ROW等于num_expert_group
数据读取和线程相关索引计算
auto* input_ptr = reinterpret_cast<T*>(input);
auto* bias_ptr = reinterpret_cast<T*>(bias);
auto* thread_row_ptr = input_ptr + thread_row * params.NUM_EXPERTS;
// 计算当前线程在一个线程组(专家组)内的索引位置
// 由于params.THREADS_PER_ROW等于num_expert_group(专家组数量)
// 这个操作将把同一个warp中的线程划分到不同的专家组中
int thread_group_idx = tidx % params.THREADS_PER_ROW;
// 计算当前线程负责处理的第一个专家的索引
// 每个线程处理params.VPT个专家,params.VPT = num_experts/num_expert_group
// 例如:对于DeepSeek V3,num_experts=256,num_expert_group=8时
// params.VPT=32,即每个线程处理32个连续的专家
int first_elt_read_by_thread = thread_group_idx * params.VPT;
-
input_ptr对应gating_output -
bias_ptr对应correction_bias -
params.NUM_EXPERTS对应num_experts -
params.VPT对应num_experts / num_expert_group
对 gating_output 应用 Sigmoid
////////////////////// Sigmoid //////////////////////
#pragma unroll
for (int ii = 0; ii < params.VPT; ++ii) {
row_chunk[ii] = static_cast<T>(1.0f / (1.0f + expf(-float(row_chunk[ii]))));
}
对应python代码中的:
scores = gating_output.sigmoid()
添加 correction_bias
////////////////////// Add Bias //////////////////////
#pragma unroll
for (int ii = 0; ii < params.VPT; ++ii) {
bias_chunk[ii] = row_chunk[ii] + bias_chunk[ii];
}
对应Python代码中的:
scores_for_choice = scores.view(num_token, -1) + correction_bias.unsqueeze(0)
通过循环排除得分最低的专家组间接实现grouped topk
////////////////////// Exclude Groups //////////////////////
// 循环num_expert_group - topk_group次,每次找到一个得分最低的专家组并将其排除
#pragma unroll
for (int k_idx = 0; k_idx < params.THREADS_PER_ROW - topk_group;
++k_idx) { // QQ NOTE Here params.THREADS_PER_ROW = num_expert_group
int expert = first_elt_read_by_thread;
// 在当前线程负责的专家中找到最大的两个值
T max_val = static_cast<T>(-FLT_MAX);
T max_val_second = static_cast<T>(-FLT_MAX);
#pragma unroll
for (int ii = 0; ii < params.VPT; ++ii) {
T val = bias_chunk[ii];
// 更新最大值和次大值
if (cmp_gt(val, max_val)) {
max_val_second = max_val;
max_val = val;
} elseif (cmp_gt(val, max_val_second)) {
max_val_second = val;
}
}
// 计算当前专家组的得分(top2得分之和)
// QQ NOTE: currently fixed to pick top2 sigmoid weight value in each expert group and sum them as the group weight
// to select expert groups
T max_sum = max_val + max_val_second;
// 在warp内进行归约,找到得分最低的专家组
#pragma unroll
for (int mask = params.THREADS_PER_ROW / 2; mask > 0; mask /= 2) {
// 使用warp shuffle操作交换数据
T other_max_sum =
static_cast<T>(__shfl_xor_sync(0xFFFFFFFF, static_cast<float>(max_sum), mask, params.THREADS_PER_ROW));
int other_expert = __shfl_xor_sync(0xFFFFFFFF, expert, mask, params.THREADS_PER_ROW);
// 比较得分,保留得分较低的专家组
// 如果得分相同,保留索引较大的专家组
if (cmp_gt(max_sum, other_max_sum) || (cmp_eq(other_max_sum, max_sum) && other_expert > expert)) {
max_sum = other_max_sum;
expert = other_expert;
}
}
// 将得分最低的专家组的所有专家得分设为FLT_MAX,相当于将其排除
if (k_idx < params.THREADS_PER_ROW - topk_group) {
// 计算需要清除的线程ID
intconst thread_to_clear_in_group = expert / params.VPT;
// 如果当前线程负责这个专家组
if (thread_group_idx == thread_to_clear_in_group) {
#pragma unroll
for (int ii = 0; ii < params.VPT; ++ii) {
bias_chunk[ii] = static_cast<T>(FLT_MAX);
}
}
}
}
// 同步所有线程,确保专家组排除操作完成
__syncthreads();
对应Python代码中的:
# 计算每个专家组的得分:
# 1. 将scores重塑为[num_token, num_expert_group, experts_per_group]
# 2. 在每个组内选择top2的得分
# 3. 对每个组的top2得分求和,得到组得分
group_scores = (
scores_for_choice.view(num_token, num_expert_group, -1)
.topk(2, dim=-1)[0]
.sum(dim=-1)
) # [n, n_group]
# 选择得分最高的topk_group个专家组
group_idx = torch.topk(group_scores, k=topk_group, dim=-1, sorted=False)[1] # [n, top_k_group]
# 创建组掩码,标记被选中的组
group_mask = torch.zeros_like(group_scores) # [n, n_group]
group_mask.scatter_(1, group_idx, 1) # [n, n_group]
# 扩展组掩码到专家级别
score_mask = (
group_mask.unsqueeze(-1)
.expand(num_token, num_expert_group, scores.shape[-1] // num_expert_group)
.reshape(num_token, -1)
) # [n, e]
# 将未选中组的专家得分设为负无穷
tmp_scores = scores_for_choice.masked_fill(
~score_mask.bool(), float("-inf")
) # [n, e]
通过循环选择topk个专家间接实现topk
////////////////////// Topk //////////////////////
// 用于存储选中专家权重的总和,用于后续归一化
float output_sum = 0.0f;
// 循环选择topk个专家
for (int k_idx = 0; k_idx < topk; ++k_idx) {
// 在当前线程的bias_chunk中找到最大值及其对应的专家ID
T max_val = bias_chunk[0];
int expert = first_elt_read_by_thread;
// 如果当前值不是FLT_MAX(说明该位置未被清除)
if (!cmp_eq(max_val, static_cast<T>(FLT_MAX))) {
// 遍历当前线程负责的所有专家,找到最大值
#pragma unroll
for (int ii = 1; ii < params.VPT; ++ii) {
T val = bias_chunk[ii];
if (cmp_gt(val, max_val)) {
max_val = val;
expert = first_elt_read_by_thread + ii;
}
}
} else {
// 如果当前值是FLT_MAX,说明该位置已被清除,将max_val设为最小值
max_val = static_cast<T>(-FLT_MAX);
}
// 在warp内进行归约,找到全局最大值
#pragma unroll
for (int mask = params.THREADS_PER_ROW / 2; mask > 0; mask /= 2) {
// 使用warp shuffle操作交换数据
T other_max =
static_cast<T>(__shfl_xor_sync(0xFFFFFFFF, static_cast<float>(max_val), mask, params.THREADS_PER_ROW));
int other_expert = __shfl_xor_sync(0xFFFFFFFF, expert, mask, params.THREADS_PER_ROW);
// 更新最大值,如果值相等则选择ID较小的专家
if (cmp_gt(other_max, max_val) || (cmp_eq(other_max, max_val) && other_expert < expert)) {
max_val = other_max;
expert = other_expert;
}
}
// 如果当前是有效的topk索引
if (k_idx < topk) {
// 计算需要清除最大值的线程ID
int thread_to_clear_in_group = expert / params.VPT;
// 计算输出数组的索引
int64_t idx = topk * thread_row + k_idx;
// 如果当前线程组是需要清除最大值的线程组
if (thread_group_idx == thread_to_clear_in_group) {
// 计算在线程内需要清除的专家索引
int expert_to_clear_in_thread = expert % params.VPT;
// 将选中的专家位置标记为已使用
bias_chunk[expert_to_clear_in_thread] = static_cast<T>(-FLT_MAX);
// 存储选中专家的权重和索引
output_ptr[idx] = static_cast<float>(row_chunk[expert_to_clear_in_thread]);
indices_ptr[idx] = static_cast<int32_t>(expert);
}
// 第0个线程组负责累加权重和
if (thread_group_idx == 0) {
output_sum += output_ptr[idx];
}
}
// 同步所有线程
__syncthreads();
}
对应Python代码中的:
_, topk_ids = torch.topk(tmp_scores, k=topk, dim=-1, sorted=False)
# 获取选中专家的原始得分作为权重
topk_weights = scores.gather(1, topk_ids)
topk_weights_sum = topk_weights.sum(dim=-1, keepdim=True)
权重归一化
////////////////////// Rescale Output //////////////////////
if (thread_group_idx == 0) {
#pragma unroll
for (int ii = 0; ii < topk; ++ii) {
int64_t const idx = topk * thread_row + ii;
output_ptr[idx] = static_cast<float>(static_cast<T>(output_ptr[idx]) / static_cast<T>(output_sum));
}
}
对应Python代码中的最后几行:
# 如果需要重新归一化,对选中的专家权重进行归一化处理
if renormalize:
topk_weights = topk_weights / topk_weights_sum
# 返回归一化后的权重和选中的专家ID
return topk_weights.to(torch.float32), topk_ids.to(torch.int32)
0x2.5 流程图
根据代码走读使用Claude 3.5 sonnet-20241022生成一个流程图如下所示:
初始化和数据预处理
┌─────────────────────────┐
│ 开始 │
└──────────┬──────────────┘
↓
┌─────────────────────────┐
│ 初始化线程索引和数据 │
└──────────┬──────────────┘
↓
┌─────────────────────────┐
│ 计算thread_row │
└──────────┬──────────────┘
↓
┌─────────────────────────┐
│ thread_row >= num_rows? │
└──────────┬──────────────┘
否 ↓ 是 → 返回
┌─────────────────────────┐
│ 数据读取和类型转换 │
└──────────┬──────────────┘
↓
┌─────────────────────────┐
│ Sigmoid激活 │
└──────────┬──────────────┘
↓
┌─────────────────────────┐
│ 添加偏置 │
└──────────┬──────────────┘
↓
专家组选择阶段
┌─────────────────────────┐
│ 专家组选择循环 │←─────┐
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ 在每个专家组内找top2得分│ │
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ 计算专家组得分sum_top2│ │
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ Warp内归约找最低分组 │ │
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ 排除最低分组 │ │
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ 完成所有组排除? │─否───┘
└──────────┬──────────────┘
是 ↓
专家选择阶段
┌─────────────────────────┐
│ 专家选择循环 │←─────┐
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ 在当前线程找最大值 │ │
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ Warp内归约找全局最大值 │ │
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ 更新输出和索引 │ │
└──────────┬──────────────┘ │
↓ │
┌─────────────────────────┐ │
│ 完成所有topk选择? │─否───┘
└──────────┬──────────────┘
是 ↓
最终处理
┌─────────────────────────┐
│ 权重归一化 │
└──────────┬──────────────┘
↓
┌─────────────────────────┐
│ 结束 │
└─────────────────────────┘
0x3. 总结
这篇blog介绍了一下如何通过cuda代码实现DeepSeek V3的biased_grouped_topk融合算子,实际上这个kernel最开始应该来自于TensorRT-LLM和Faster-Transformer中,后续被持续优化和apply到了DeepSeek V3这里,是一个非常经典的CUDA kernel在推理框架中的优化实现。
(文:GiantPandaCV)
