白交 一水 发自 凹非寺
量子位 | 公众号 QbitAI
快来围观,陶哲轩当视频博主了。
第一个产出就很炸裂:人类需要写满一页纸的证明,结果借助AI 33分钟就搞定了?!

整个过程看起来一气呵成,还是全程“盲证”不用过脑子那种。
对于这一操作,网友们惊呆:这具有足够的历史意义。


在没有明显引导、宣传之下,他的订阅数一天时间已经有900+,观看数超两千,目前仍然在高速增长中。
大家赶在爆火之前留言:
今天我们相聚在这里,就是为了见证伟大数学频道的诞生。

具体来看看是如何做到?
33分钟盲证定理
陶哲轩这次选取了泛代数中的一个命题,即证明Magma方程E1689蕴含E2。
方程具体是什么不重要,我们只需要了解,即使是方程理论项目的合作者Bruno Le Floch,也足足人工花了一页纸才完成证明。
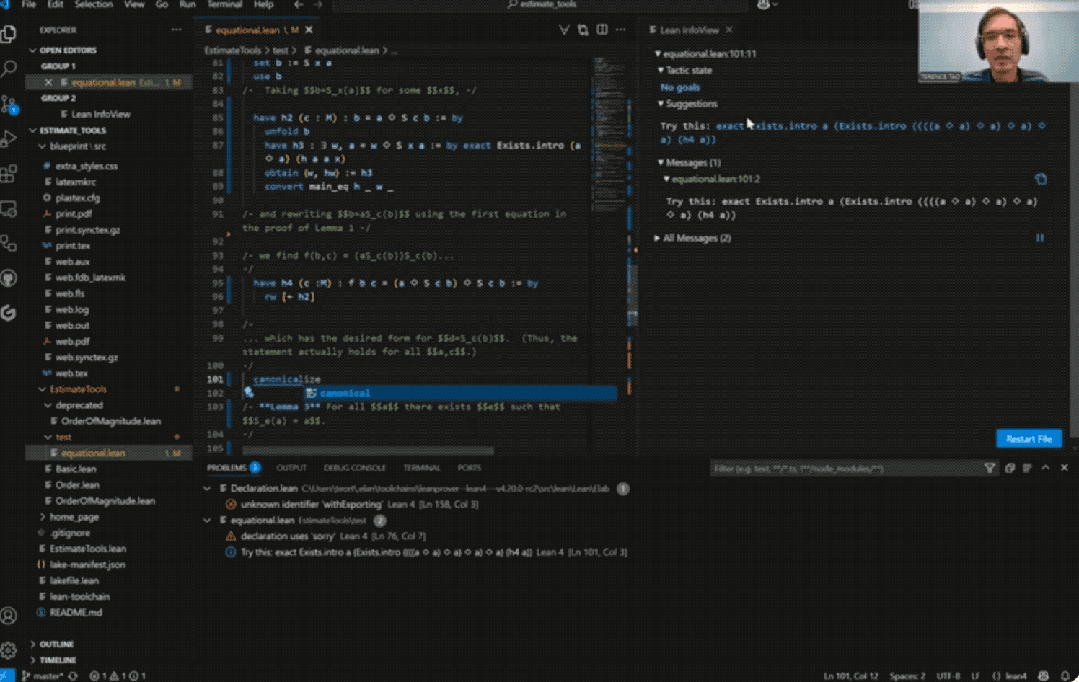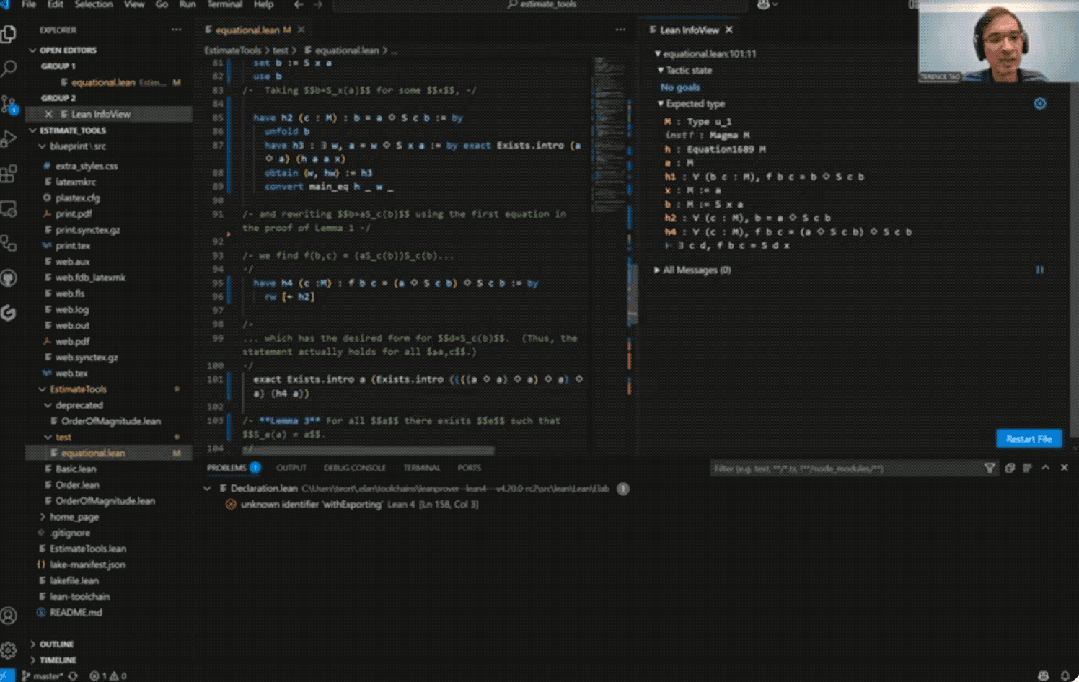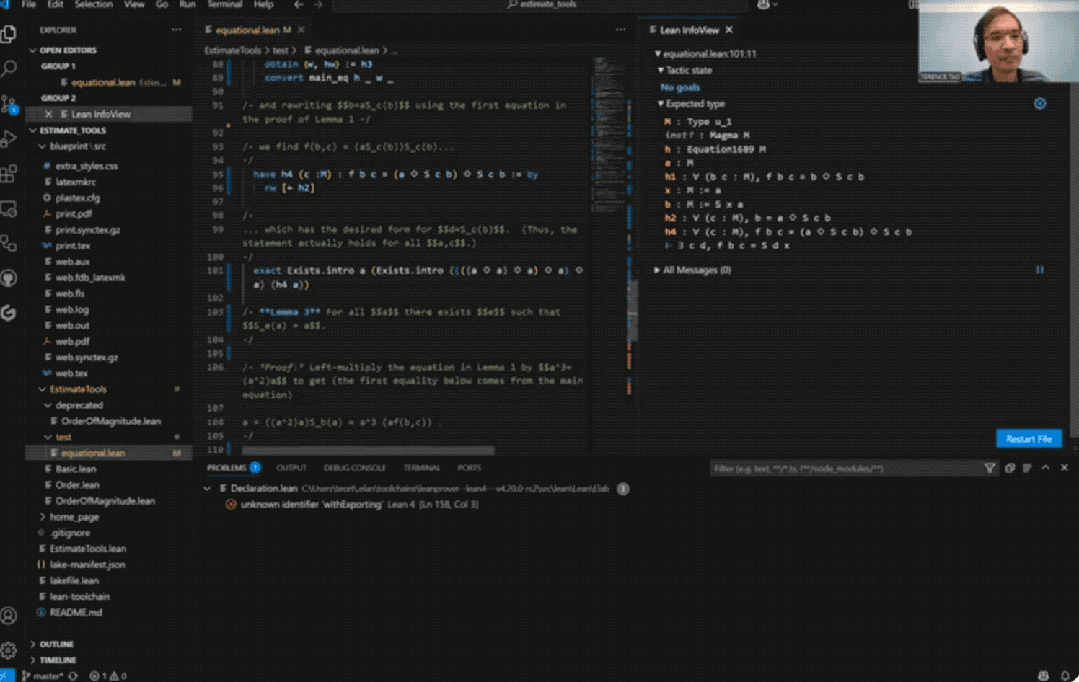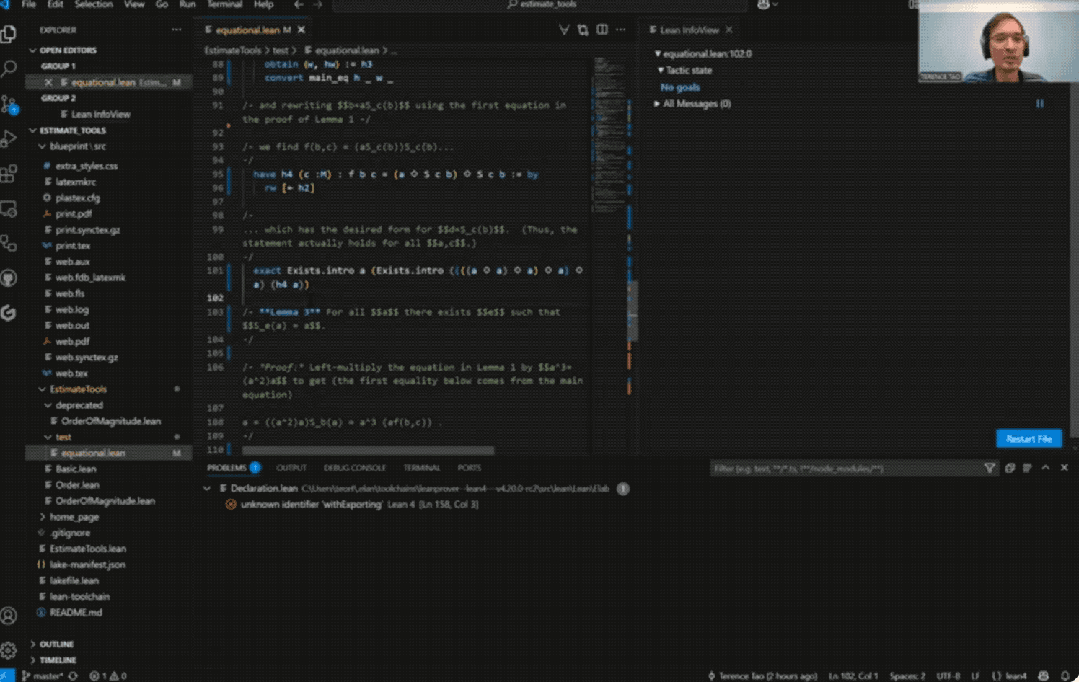
而用上AI后,整个证明过程仅用时33分钟:
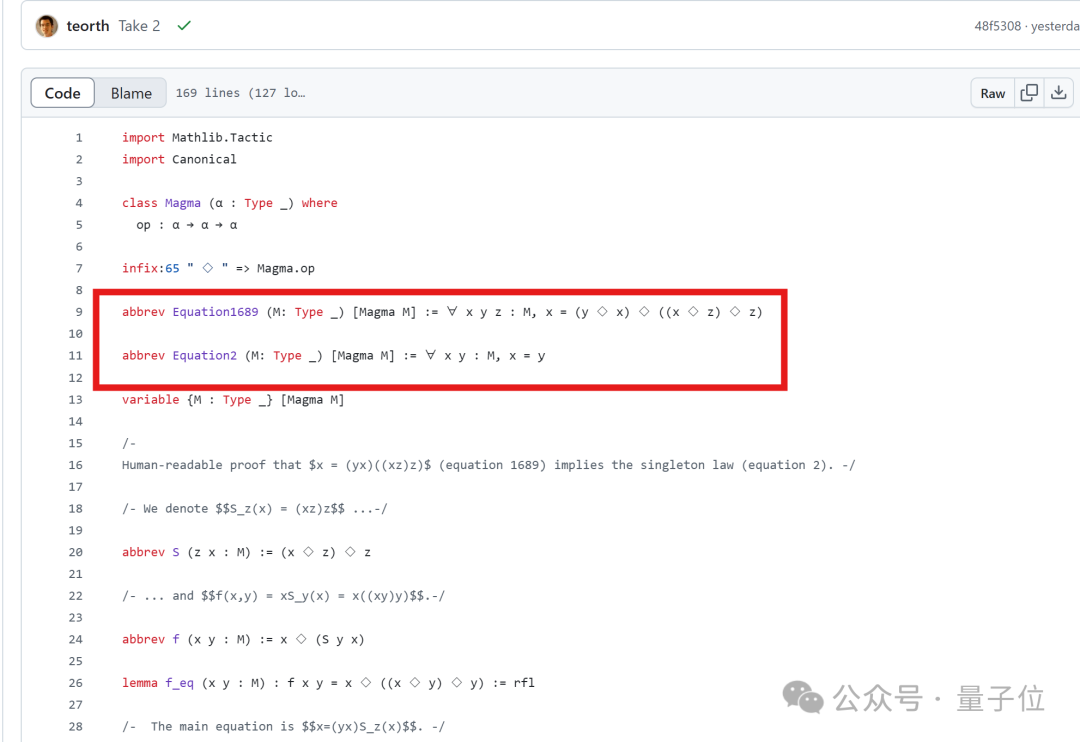
具体而言,陶哲轩尝试完全基于Bruno Le Floch的草稿,逐行进行形式化。
他将草稿拆分为微小逻辑单元,交由GitHub Copilot生成代码骨架,再以Lean的canonical策略匹配填补细节,过程中也涉及部分手动补全。
最终,整个形式化证明能够在Lean中通过验证。
不仅时间大大缩短了,更重要的是满足了“人类可读性”。
要知道Bruno Le Floch最初挑战该问题时,曾在论文中宣称E1689-E2的所有已知证明都依赖计算机辅助。
直到后来他使用prover9 ATP(自动定理证明器)给出了一个更具可读性的人类版本,所以才对之前的想法产生动摇:
它是否仍然可以被认为是计算机辅助的,我不确定。
针对这一疑惑,陶哲轩提议今后可以在论文中明确说明,虽然最初的证明是由计算机生成的,但在项目进行过程中,研究者们成功地将其转化为一个人类可读的证明。

并且为了实际验证AI能在多大程度上开启自动化形式证明,陶哲轩就此开启了本次YouTube首秀。
通过几次亲自尝试,陶哲轩得出了如下结论:
这种半自动化的方法适用于那些技术性强、概念性弱的论证,即那些主要关注细节准确性而非整体概念理解的证明。
并且他再一次强调,AI辅助证明能够把数学家从一些相对不重要的繁琐事务中解放出来,“让AI去做一些它擅长的事”。
在他看来,尽管最终的结果“并不优雅”,但它体现了AI辅助证明的巨大潜力。

最后需要说明一下,陶哲轩并非一次就成功了。
据他在视频中透露,前两次的证明过程都出现了一些“bug”——
第一次拿到的代码才到第5行他就有点看不懂了,所以选择了重开;第二次虽然完成了所有证明(用时48分钟),但由于是新人博主不太熟悉录屏设备,导致屏幕分享失败,因此又只能重来。

数学证明助手迎来2.0版本
此外,还有他开发的数学证明助手迎来2.0版本升级。

根据介绍,这是一个用Python开发的轻量级证明助手,其功能远逊于Lean、Isabelle或Rocq等完整证明助手,但(希望)它能够轻松用于证明一些简短而繁琐的任务。
一个具体的目标是,为渐近分析提供支持。
两周前,在大模型的帮助之下,他花了四个小时编程得到了这么一个概念验证工具。
结果不到两周,这个工具就迎来了全面改进——
首先,将其改造成一个基本的证明助手,使其能够处理一些命题逻辑;其次,根据反馈,这个证明助手变得更为灵活(在几个关键方面刻意模仿精简证明助手)。
目前这个助手有两种模式:假设模式和策略模式。其中策略模式作为默认模式,有点类似于Lean、Isabelle或Rocq里面那样式儿的策略模式。
目前策略列表主要分为四类:
-
命题策略(主要围绕通过布尔运算操纵命题) -
线性算术策略(依赖于线性规划及其变体) -
替代策略——用一个假设或目标替代另一个假设或目标的各种技术 -
简化策略——利用其他可用假设来“简化”假设或目标的方法
当然这些还不是全部,这个助手支持扩展,大家可以在里面进行添加。
举个例子。
如果x,y,z是正实数,且x<2y和y<3z+1,证明x<7z+2。
将它形式化就会变成:
>>> from main import *>>> p = linarith_exercise()Starting proof. Current proof state:x: pos_realy: pos_realz: pos_realh1: x < 2*yh2: y < 3*z + 1|- x < 7*z + 2
证明助手接收到指令后,指导助手使用各种“策略”来简化问题,直到问题得到解决。
那么这个问题可以通过线性算术Linarith()求解。
>> p.use(Linarith())Goal solved by linear arithmetic!Proof complete!
如果想要有详细解释,也是OK的:
>>> from main import *>>> p = linarith_exercise()Starting proof. Current proof state:x: pos_realy: pos_realz: pos_realh1: x < 2*yh2: y < 3*z + 1|- x < 7*z + 2>>> p.use(Linarith(verbose=true))Checking feasibility of the following inequalities:1*z > 01*x + -7*z >= 21*y + -3*z < 11*y > 01*x > 01*x + -2*y < 0Infeasible by summing the following:1*z > 0 multiplied by 1/41*x + -7*z >= 2 multiplied by 1/41*y + -3*z < 1 multiplied by -1/21*x + -2*y < 0 multiplied by -1/4Goal solved by linear arithmetic!Proof complete!
可以看到,首先,它通过反证法进行论证,即采用否定x≥7z+2目标x<7z+2并将其添加到假设中。
然后,它将假设中所有不等式转化为“线性规划”形式,变量在左边,常数在右边。
最后,它使用精确线性规划来寻找这些不等式的线性组合,从而导致荒谬的不等式,在这种情况下0<1。
解决完问题之后,还可以使用proof()进行检查。
有时候,遇到证明过程会涉及案例拆分的情况,那么证明助手最终会呈现树状结构。
对于这个证明助手,陶哲轩表示:非常满意,并且愿意接受进一步的建议或贡献新的功能。比如引入新的数据类型、公例和策略,或者贡献一些有难度的例子。
此外还计划开发用于估算符号函数的函数空间规范的工具。例如创建部署霍尔德不等式和索博列夫嵌入不等式等定理的策略。看起来sympy框架足够灵活,可以为这类对象创建更多的对象类。
感兴趣的旁友,可以前往去体验下哦。
(文:量子位)
