©PaperWeekly 原创 · 作者 | 于星橦
个人主页 | https://xingtongyu.netlify.app/

现实世界中不同对象之间的复杂关系可以用图来表示,而图神经网络是图学习的主流技术,但其性能在很大程度上依赖于大量的标注数据。
为了减少对有标注数据的需求,预训练和提示学习方法已成为一种流行的解决方案。然而,现有的提示方法并未区分现实世界中图的同配和异配性:许多现实世界的图是非同配的,并非严格的同配或异配,而是混合了同配和异配模式,在不同的图和节点中表现出不同的非同配性质。
在本文中,我们提出了 ProNoG,一种针对这些非同配图的新型预训练和提示学习框架。
Non-Homophilic Graph Pre-Training and Prompt Learning
论文链接:
https://arxiv.org/pdf/2408.12594v2
代码链接:
https://github.com/Jaygagaga/ProNoG/tree/main
论文录用:
The ACM SIGKDD Conference on Knowledge Discovery and Data Mining Research Track 2025
首先,我们分析了现有的图预训练方法,提供了非同配图上预训练任务选择的理论分析。其次,我们认识到每个节点都具有独特的非同配特征,并提出了一种条件网络来表示下游任务中节点特定的非同配性质。我们通过在十个公共数据集上的广泛实验,评估和分析了 ProNoG,展现了其有效性。


理论分析:非同配图的预训练方法
本文理论分析了非同配图上图的对比学习预训练方法的优劣。首先,所有图对比学习方法可以定义为如下形式,其中 为目标实例(节点/图), 和 分别代表 的正负样本。

基于此,我们给出了两个定义:
定义 1:同配任务
在一个图 上,一个预训练任务 是一个同配任务,当且仅当:对于所有 ,所有 ,所有 ,满足以下条件:。相对地,不属于同配任务的任务被称为非同配任务。
定义 2:同配样本
在图 上,考虑一个三元组 ,其中 , ,且 。三元组 是一个同配样本,当且仅当:。否则,它是一个非同配样本。
我们在下表中提供了一些常见的同配任务和非同配任务的细节。
基于此定义,我们证明了两个定理:
定理1:对于一个同配任务 ,加入一个同配样本总是会比加入一个非同配样本导致更小的损失。
定理2:考虑图 上的标签映射函数 ,令 为 映射的标签。假设该标签映射满足以下条件:。令 表示图 上同配任务 的同配样本的期望数量。那么,随着相对于 定义的同配率的增加, 单调递增。
基于上述两条定理,我们可以得出结论:对于非同配图,特别是同配率低的图,使用非同配任务往往比使用同配任务具有更大的优势。本文中我们使用 GraphCL 作为预训练任务。

方法:非同配图的提示学习
我们提出了 ProNoG :针对非同质性图的提示学习框架。其中包含两个部分:提示的生成和提示的优化过程。
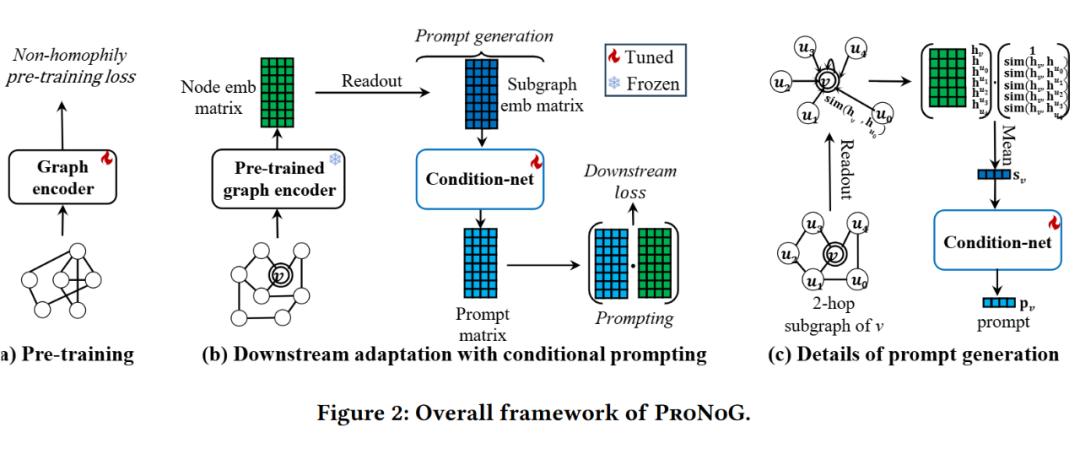
在非同配图中,不同的节点表现出独特的非同配性。具体来说,不同的节点通常具有多样的同配率,这表明它们与邻居节点之间存在不同的拓扑结构。此外,即使同配率相似的节点,其邻域分布也可能由于邻居节点的同配率不同而存在差异。
因此,与标准图提示学习中为所有节点学习单一提示的方法不同,我们设计了一个条件网络来生成一系列基于非同配特性的条件提示。由此,为每个节点都生成了自己独特的提示,旨在适应其独特的非同配特性。
首先,我们通过节点的多跳邻域来表示其非同配特性。具体来说,对于一个给定的节点 ,我们读取其 -跳的子图 ,包含节点 及在最多 步内可从 到达的节点。
然后,对于每个下游任务,我们的目标是为每个节点分配一个唯一的提示向量。然而,直接对这些提示向量进行参数化会显著增加可学习参数的数量,这可能会导致在少样本场景中过拟。
为了以最少的参数满足每个节点的独特非同配特性,我们提出条件网络来生成节点特定的提示向量。
具体来说,以节点 的子图表示 作为条件,条件网络生成一个关于任务 的节点 的唯一提示向量,表示为 ,如下所示:,其中, 是由参数 控制的条件网络。它输出一个唯一的提示向量 ,该向量根据条件 变化,表示节点 的非同配特性。
需要注意的是,这是一种超网络的形式,它使用一个次级网络生成主网络中基于输入特征的参数。在我们的场景中,条件网络是次级网络,用于生成提示参数,而不会扩展主网络中可学习参数的数量。
3.2 提升优化
在本文中,我们关注两种常见的下游任务:节点分类和图分类。提示优化过程并不直接优化提示向量,而是优化条件网络,该网络随后为给定的下游任务生成提示向量。
我们利用基于节点/图相似性的损失函数,对于一个标注训练集 \)的任务 ,其中 可以是一个节点或一个图, 是来自类别集合 的 的类别标签。
下游任务的损失函数为:
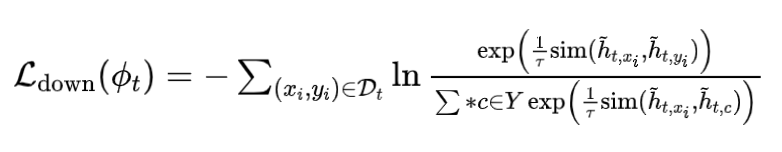
其中, 表示任务 中节点 /图 的输出嵌入。在提示调优过程中,我们仅更新条件网络的轻量化参数,同时冻结预训练 GNN 的权重。因此,我们的提示调优具有参数高效性,并且适合少样本场景。

我们在八个基准数据集上进行了全面的实验,以评估所提出的 ProNoG 在少样本节点分类和图分类任务上的有效性。
4.1.1 1-shot节点分类和图分类
我们观察到:ProNoG 在所有设置中均超越了基线方法,节点分类的表现比最好的竞争方法高出多达 21.49%,图分类高出 6.50%。这些结果表明,ProNoG 在从非同配图中学习先验知识以及捕捉节点特定非同配特性方面具有很高的有效性。

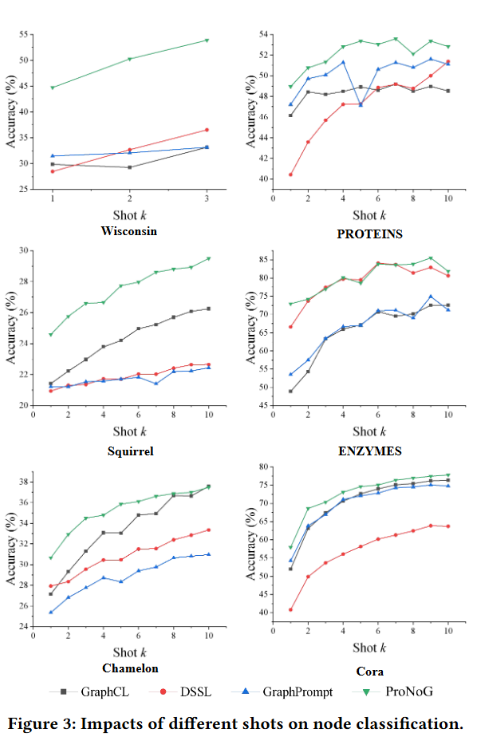
4.1.2 有标签样本数目的影响
为了评估 ProNoG 在不同标注数据量下的性能,我们在下游任务中改变样本数量。需要注意的是,由于 Wisconsin 和 Cornell 数据集中节点数量有限,我们仅执行最多 3-shot 的任务。我们观察到:ProNoG 在标注数据非常有限的低样本场景(例如 )下显著超越所有基线方法,展现了我们方法在这些情况下的有效性。
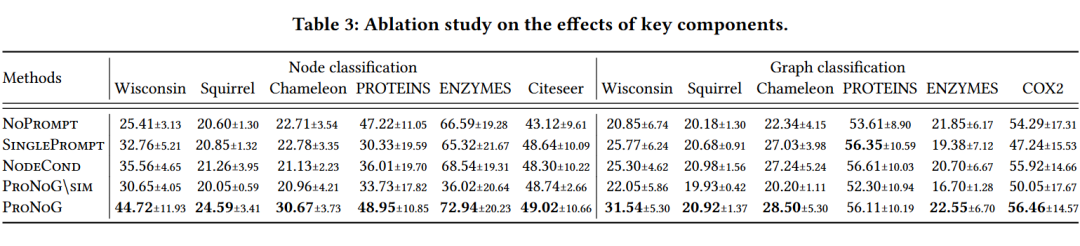
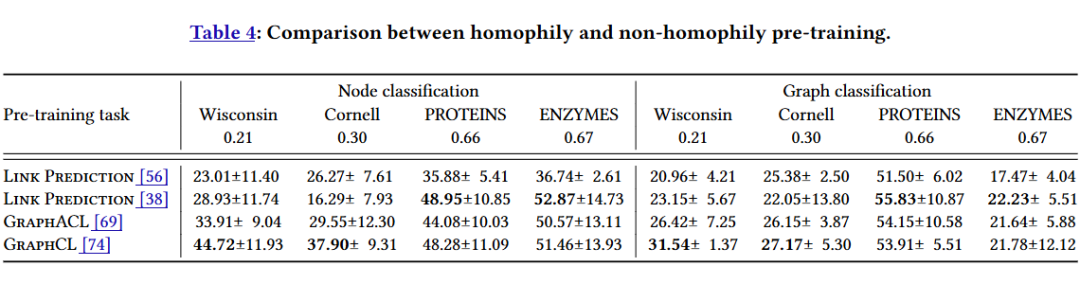
4.2 消融实验
为了全面了解 ProNoG 中每个部分的影响,我们进行了消融实验分析,证明了每个部件的重要性。
我们分别对比了同配任务(两种不同的链接预测),以及 两种不同的非同配任务(GraphCL 和 DSSL )。我们观察到,对于具有低同配率的图,非同配任务显著优于同配任务。相反,对于具有高同配率的图,这两种方法的结果各有其优劣势。
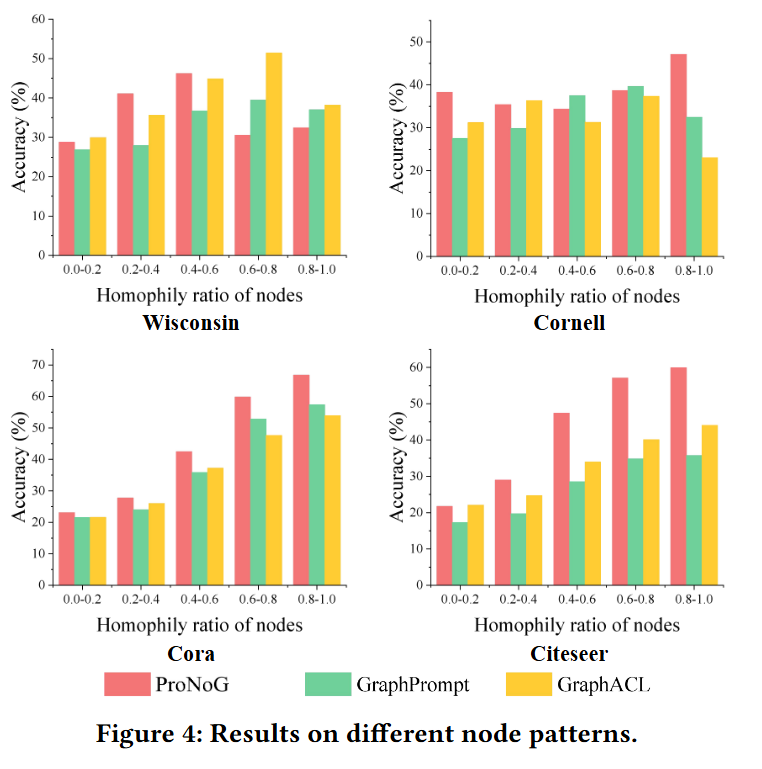
我们计算了在具有不同同配率的节点组上的准确率,并观察到,ProNoG 在所有同配特性的节点上始终优于其他模型或有竞争力,无论其同配率如何。这些结果进一步证明了 ProNoG 在捕捉节点同配特性方面的有效性,并突出了我们提出的条件提示方法的优势。
(文:PaperWeekly)