ICCV 2025｜突破线性注意力瓶颈！MALA：记忆Query幅值的神经注意力机制

本文目录

1MALA：幅值感知的线性注意力机制
(来自中科院，国科大)
1 MALA 论文解读
1.1 MALA 论文背景
1.2 Preliminary
1.3 Linear Attention 的问题：忽略幅值
1.4 幅值感知的线性注意力机制
1.5 实验结果

太长不看版

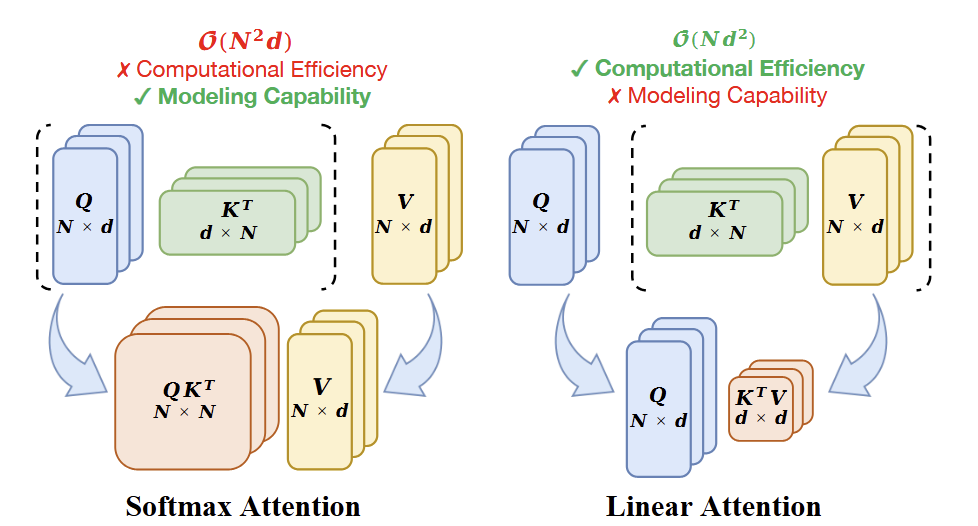
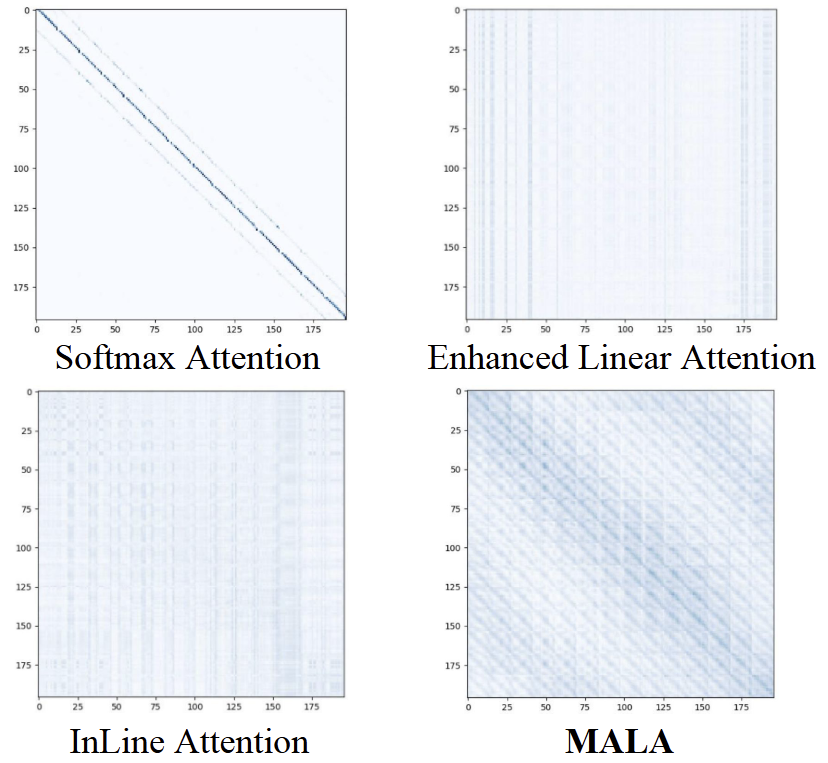
Softmax Attention 是有很好的全局建模得能力。但是其二次方的计算复杂度也比较影响其在视觉任务中的应用。反之，Linear Attention 与 Softmax Attention 具有相似的公式，同时实现线性复杂度，来进行高效的全局信息建模。然而，如图 1 所示，与标准 Softmax Attention 相比，线性注意力会遭受显着的性能下降。

本文分析了这个问题的潜在原因，发现：Linear Attention 完全丢弃了 Query 中的幅值信息 (Magnitude Information)。这会阻碍 Attention Score 动态地适应 Query 的 Scale。带来的问题就是：尽管在结构上与 Softmax Attention 相似，但是 Attention Score 的分布却大不相同。

基于此观察，本文提出了幅值感知的线性注意力 (Magnitude-Aware Linear Attention，MALA) 。MALA 将 Query 的幅值融合进了 Linear Attention 的计算中。这调整允许 MALA 生成与 Softmax Attention 非常相似的注意力分数分布，同时表现出更平衡的结构。

1 MALA：幅值感知的线性注意力机制

论文名称：Rectifying Magnitude Neglect in Linear Attention (ICCV 2025)

论文地址：

https://arxiv.org/pdf/2507.00698

代码链接：

https://github.com/qhfan/MALA

1.1 MALA 论文背景

Softmax Attention 卓越的全局建模能力使视觉 Transformer 在各种视觉任务中取得优异的性能，如图像分类、目标检测和语义分割。但是，Transformer 的核心算子 Softmax Attention具有相对于 token 数量  呈现二次方的计算复杂度，计算成本高，阻碍了其在视觉领域的广泛应用。

Linear Attention 从根本上消除了 Softmax 操作。如图 1 所示，通过删除 Softmax 操作，重新排列  的计算顺序，使得 Linear Attention 具有相对于 token 数量  呈现线性的计算复杂度。虽然 Linear Attention 和 Softmax Attention 的形式非常相似，但是 Softmax 操作去掉了之后还是会带来一些挑战，比如性能严重变差。

1.2 Preliminary

给定一个长度为  和维度  的输入标记序列  ，第  个标记  的输出可以表示为：

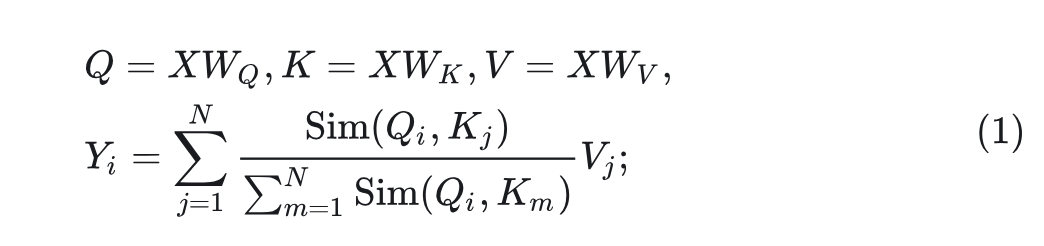
其中， 为可学习矩阵， ) 是相似度函数。经典的 Softmax Attention 中，  。这需要计算每对 Query 和 Key 的指数值，带来  的复杂度。

Linear Attention 采用核函数  来近似相似度函数，并将  和  映射为正实数。相似度函数为  。基于这种转换，Linear Attention 可以改写为：

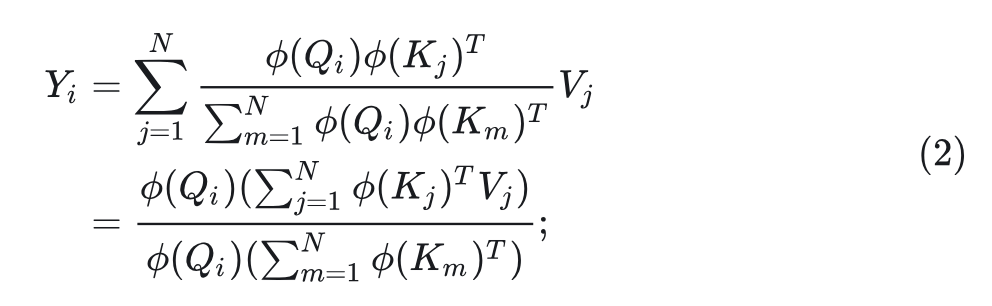
在这种计算形式中， 的操作顺序从  变为  。Linear Attention将计算复杂度从  降低为  。但是，计算复杂性的降低也会相应地导致性能下降。

1.3 Linear Attention 的问题：忽略幅值

本文分析了 Linear Attention 的计算公式，并观察到它完全忽略了 Query 的幅值信息，只保留其方向分量。因此，与 Softmax Attention 相比，Linear Attention 在注意力分数分布方面表现出显著的差异。

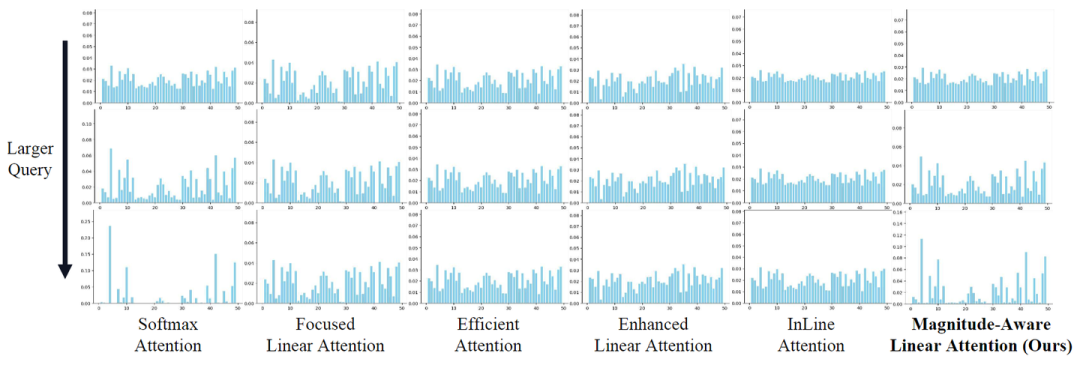
具体来讲，如图 2 所示，对于固定方向，随着 Query 的幅值增加，Softmax Attention 中的 Attention Score 分布变得越来越尖峰 (spiky)，把更多的注意力集中在 Attention Score 原本就比较高的 Key 上面。相比之下，由于计算方式本身的问题，Linear Attention 常常做不到这点，它要么保持固定的 Attention Score 分布，要么变化很小。

这个现象可能可以解释为啥 Linear Attention 的 local perception 很弱，以及很容易产生过度平滑的  Attention Score[1][2]。

这个现象作者也给了一些分析：

定义：

其中， 表示  的幅值（Magnitude），  表示其方向向量。将此表达式代入 Linear Attention 的公式，得到：

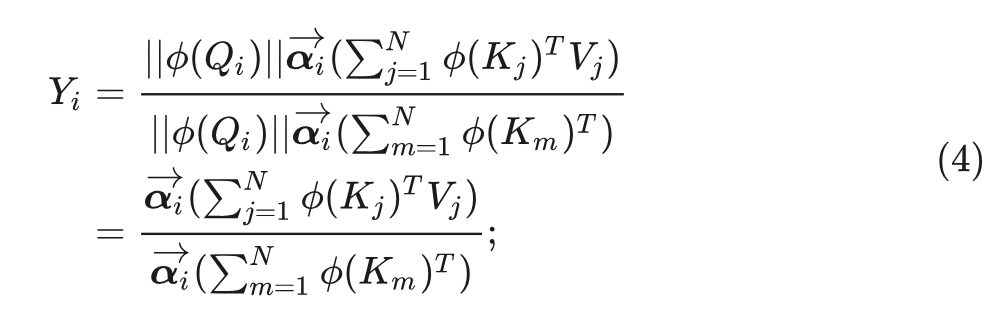
从上式中我们可以观察到 Linear Attention 中  的大小信息完全被忽略。因此，只要 保持固定，Linear Attention 的 Attention Score 的分布就可以保持不变。

这种现象导致 Linear Attention 和 Softmax Attention 的注意力分数分布存在显著的差异。在 Softmax Attention 中，完全考虑了  的大小。给定  之后，那两个不同的 Key：  的 Attention Score 之比由下式给出：

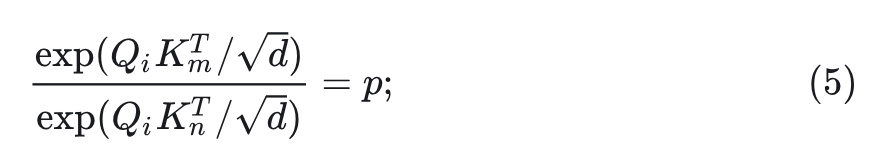
现在假设  为  分配了更高的注意力权重，即  。当  的方向保持不变并且其大小乘以  时， 的 Attention Score 之比变为：

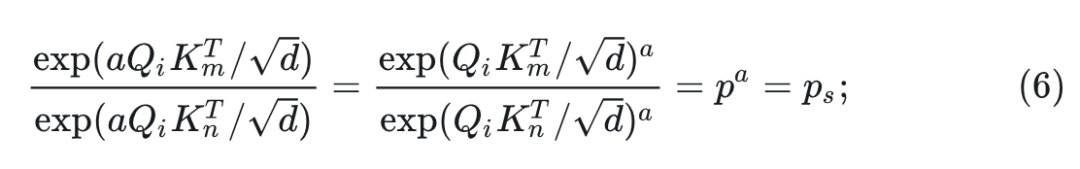
式中，由于  ，因此  。

由于  在所有的  上的 Attention Score 的总和为 1 ，式 5 和 6 表明，随着  的幅值  的增加， 的注意力变得更加集中于＂原本 Attention Score 较高的 Key＂上面，而越来越不集中于＂原本 Attention Score 较低的 Key＂上面。

然而，对于 Linear Attention，这种情况不会出现。  与  的 Attention Score 之比由下式给出：

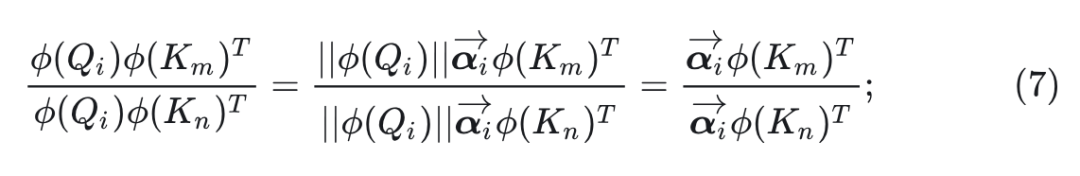
式 7 表明，无论  的大小如何变化，Linear Attention 中的 Attention Score 始终保持相同的分布，不会聚焦于特定的 Key。这种区别解释了为什么与 Softmax Attention 相比， Linear Attention 学习的注意力分数不那么尖峰，以及为什么学习到的特征表现出较弱的局部性。

除了上述理论分析外，作者还进行了实验验证。如图 3 所示。基于 DeiT－T，作者将 Softmax Attention 中的  重写为  ，从而忽略幅值信息。可以观察到模型性能显着下降，与基于 Linear Attention 的模型的性能相似。

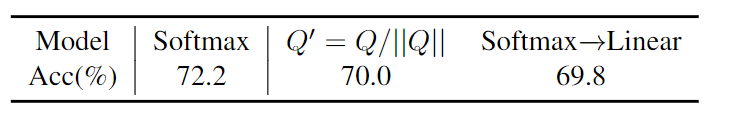
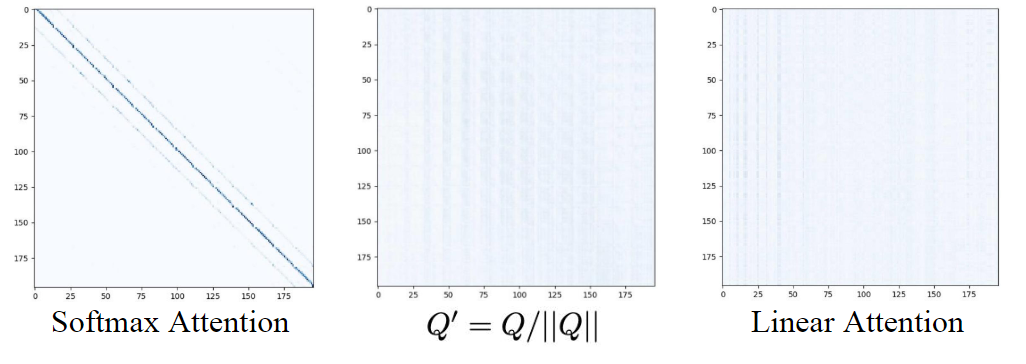
作者在图 4 中可视化了注意力分数，发现分布收敛到 Linear Attention 的分布，变得更加平滑和失去局部性。

1.4 幅值感知的线性注意力机制

为了弥合 Linear Attention 和 Softmax Attention 之间的差距，本文的目标是在 Linear Attention 中融入幅值信息  ，并表现出与 Softmax Attention 相似的变化趋势。

本文提出了幅值感知的线性注意力机制 (Magnitude-Aware Linear Attention, MALA)。MALA 引入了一个 scaling factor 和一个 offset term，同时丢弃基于除法的归一化，改为基于加法的归一化：

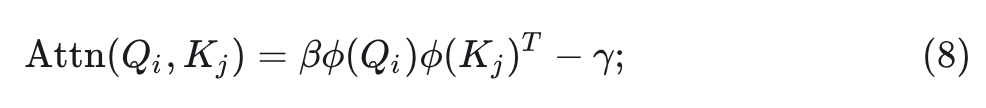
式中，

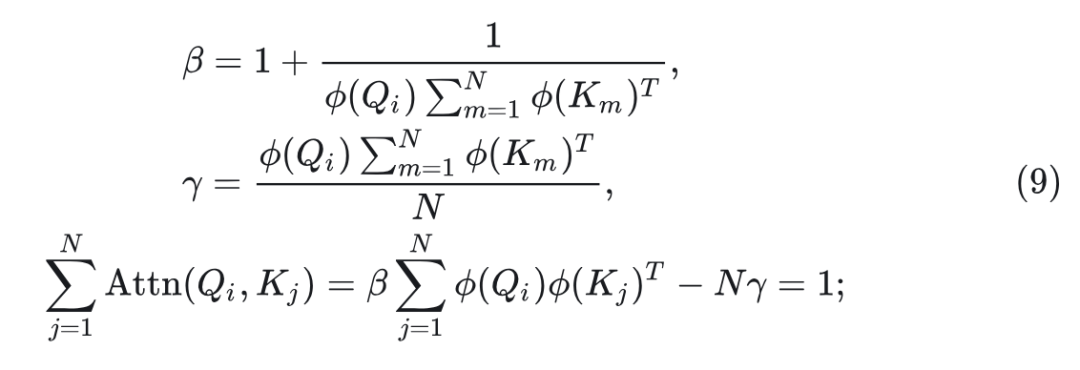
当将所有 Attention Score 视为正值时，  对  和  的 Attention Score 之比由下式给出：

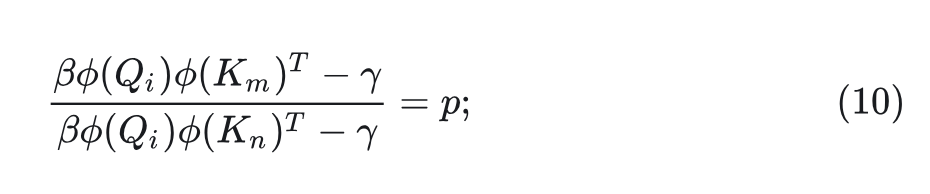
假设  给  分配了更高的 Attention Score，即  以及  。当  的方向保持不变，其大小乘以  时，新的  和  可以写成：

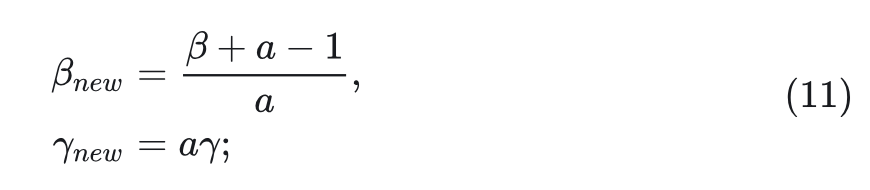
此时，  对  和  的 Attention Score 之比变为：

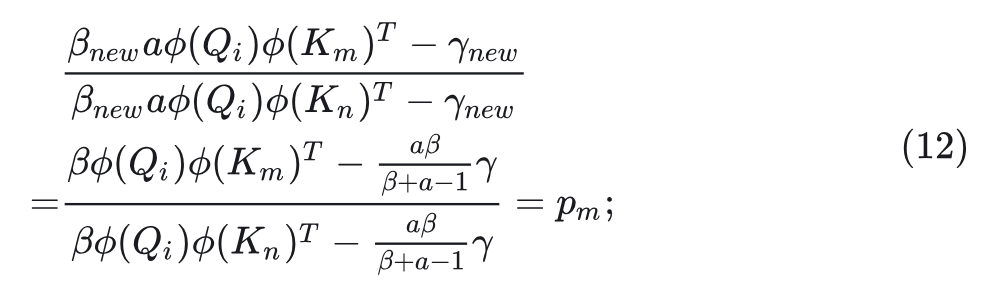
式中，由于  以及  ，可以直接证明  。［证明 1］

据此我们可以进一步证明，当将所有注意力分数视为正值时， 。［证明 2］

此外，由于  ，随着  的大小的增加，MALA 更多地关注那些原本就具有更高 Attention Score 的 Key，更少地关注那些原本就具有更低 Attention Score的 Key，这种行为类似于 Softmax Attention。

证明 1：   。

证： 因为  ，则：

展开有：

因为  ，因此  。根据式 14，有：

得证。

证明 2： 。

证： 定义：

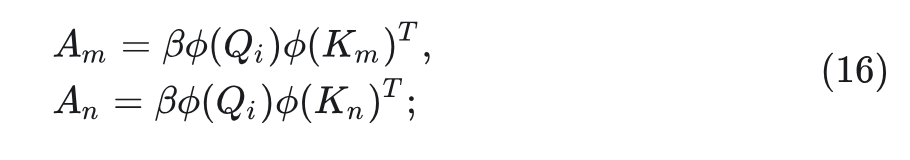
假设  将更多的注意力分配给  ，因此有： 。考虑一个  的函数：

函数  对  的导数可以写成：

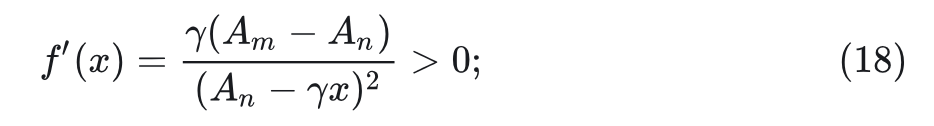
根据式 10 ，推出  。

根据式 12 ，推出  。

根据式 15， 成立。又因为函数  对  单调递增，有：  。因此： 。

得证。

尽管随着  或  的大小的增加，Softmax Attention 和 MALA 都表现出更集中的注意力分数分布的趋势，但两者的速率不同。

从式 6 中可以看出，在 Softmax Attention 中，Attention Score 的比值  相对于  的 scaling factor  呈指数增长。

从式 12 中可以看出，在 Linear Attention 中，Attention Score 的比值  相对于  的 scaling factor  呈分数增长。

MALA 中  的变化小于 Softmax Attention 中的变化，可能会帮助 MALA 在性能上优于 Softmax Attention。

如图5所示，可视化了不同机制的 Attention Score。可以看出，Softmax Attention 的分数太 spiky，主要关注局部区域。相比之下，Linear Attention 的分数过于平滑，过度忽略局部信息。MALA 有效地平衡了这两个方面，表明 MALA 中  的逐渐变化会导致 Attention Score的分布更合适。

再把 Value 考虑进去，得到 MALA 的完整公式为：

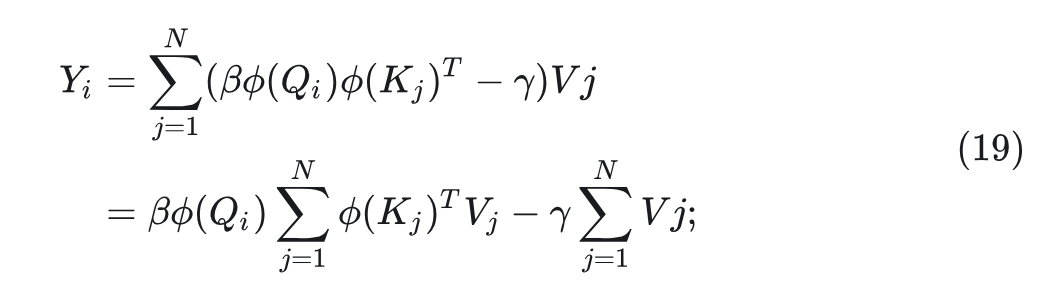
式中，

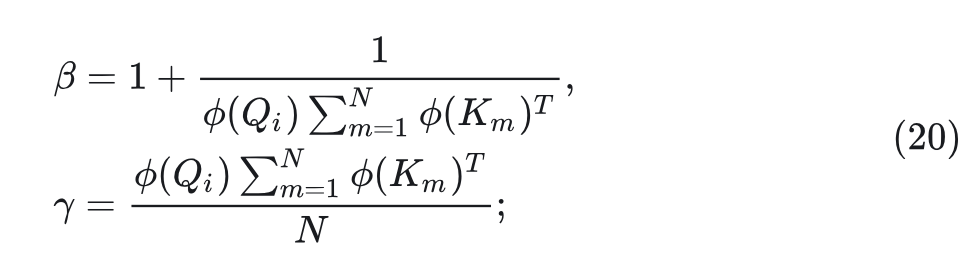
1.5 实验结果

ImageNet 图像分类

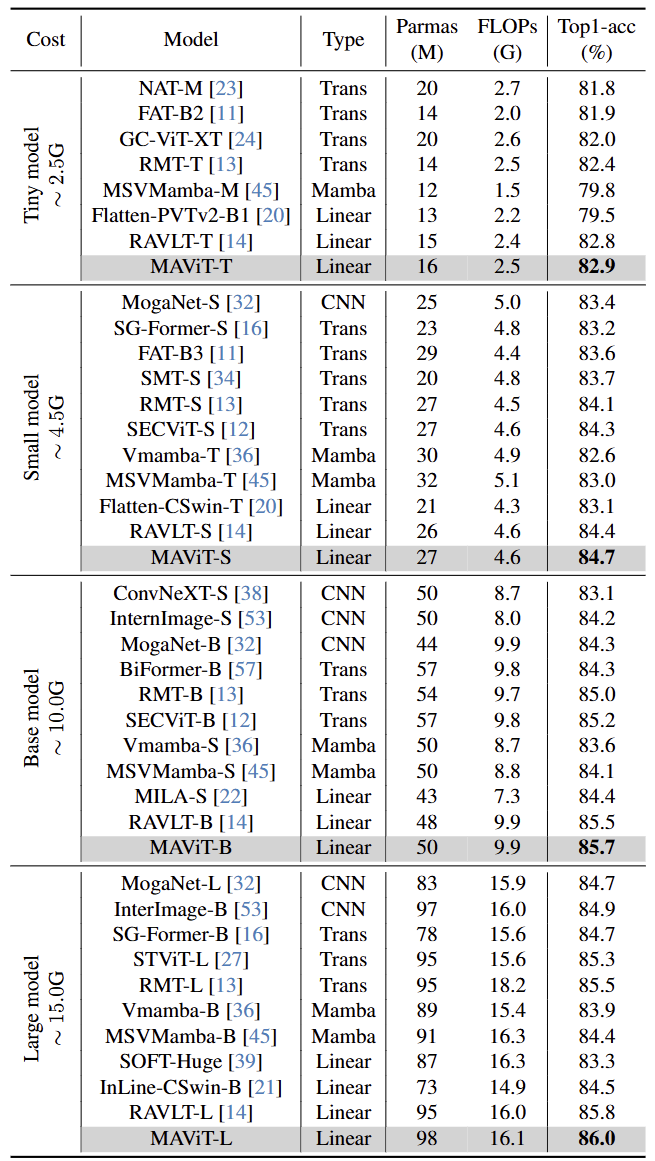
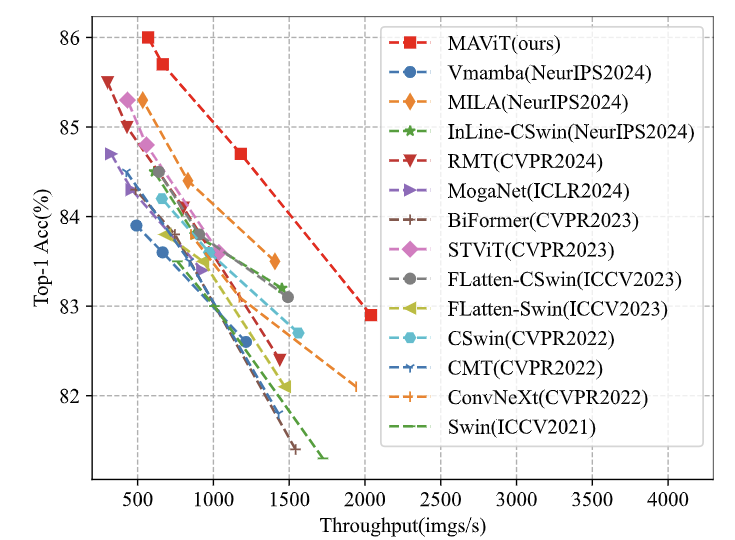
图 6 是 ImageNet-1K 实验结果。在模型大小相当的情况下，MAViT 取得了最好的结果。使用 98M 参数和 16.1G FLOPs，MAViT-L 达到了 86.0% 的精度。这结果超过了 Linear Attention 方法 MILA，提高了 0.7%。此外，MAViT-S 仅使用 27M 参数和 4.6G FLOPs 实现了 84.7% 的精度，超过了更大的 MILA-S。

目标检测和实例分割

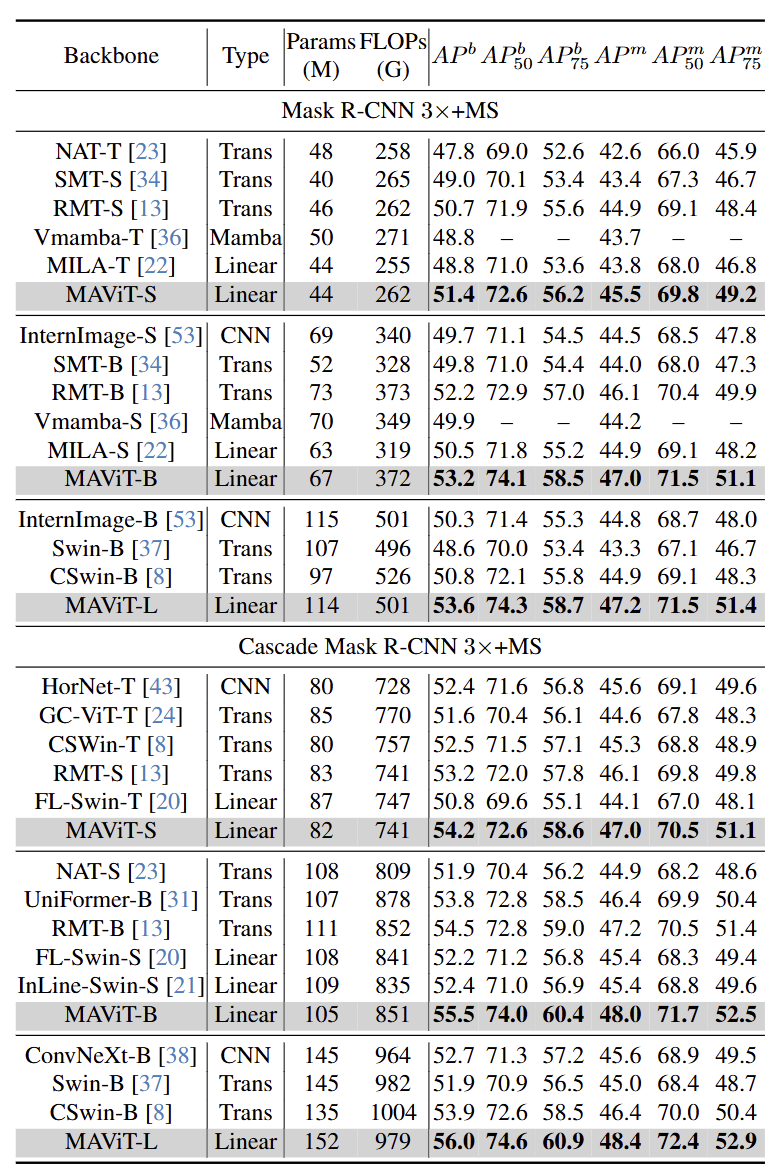
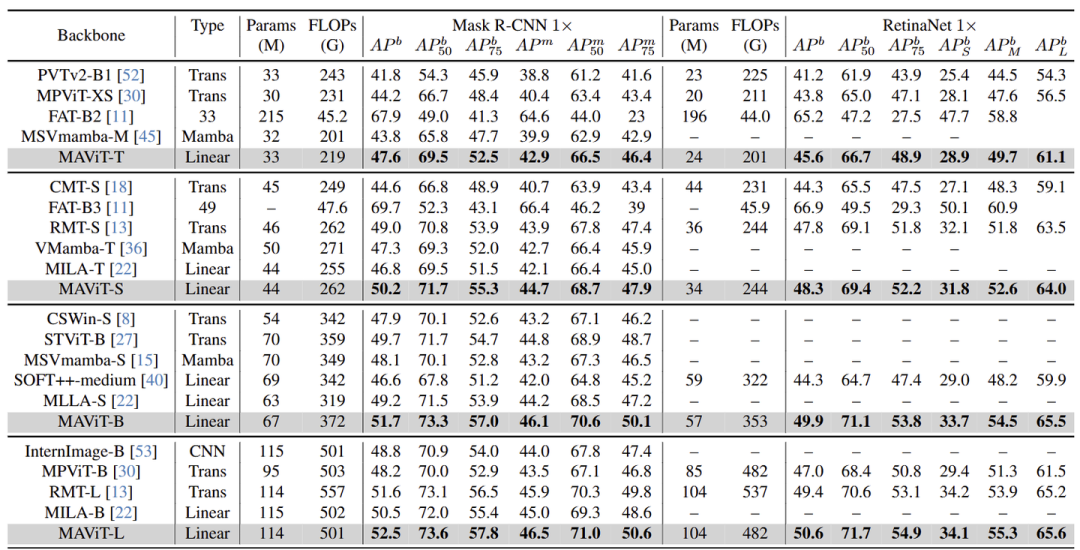
如图 7 和 8 所示，MAViT 与基于 Linear Attention 的其他模型相比表现出显著的优势。此外，它在所有模型尺度上超越了利用 Softmax Attention 的模型。具体来说，MAViT-B 在 Cascade Mask R-CNN 框架下实现了 55.5APb 和 48.0APm，甚至超过了更大的 CSwin-B (53.9APb 和 46.4APm)。

语义分割

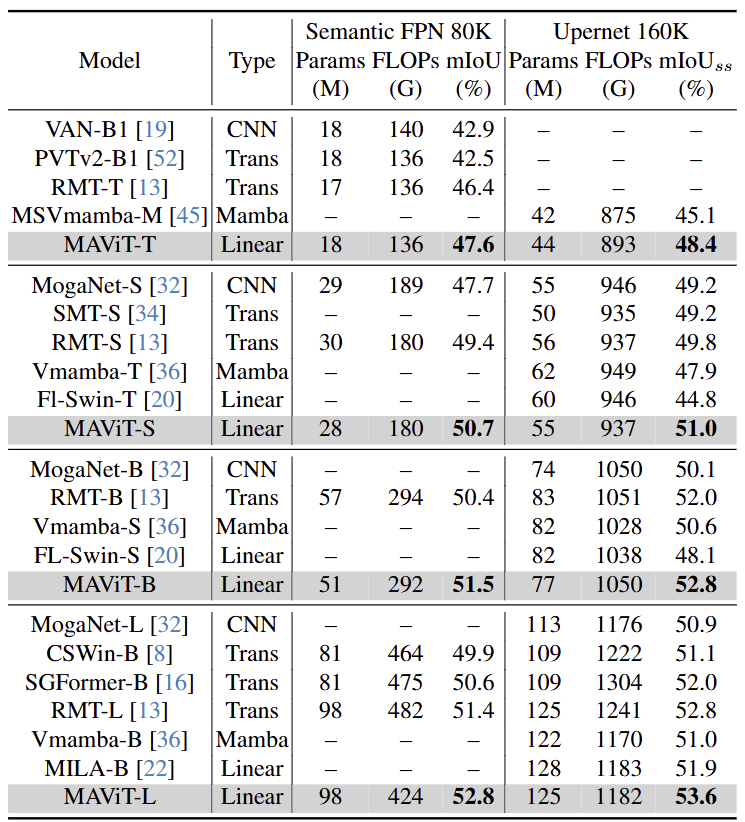
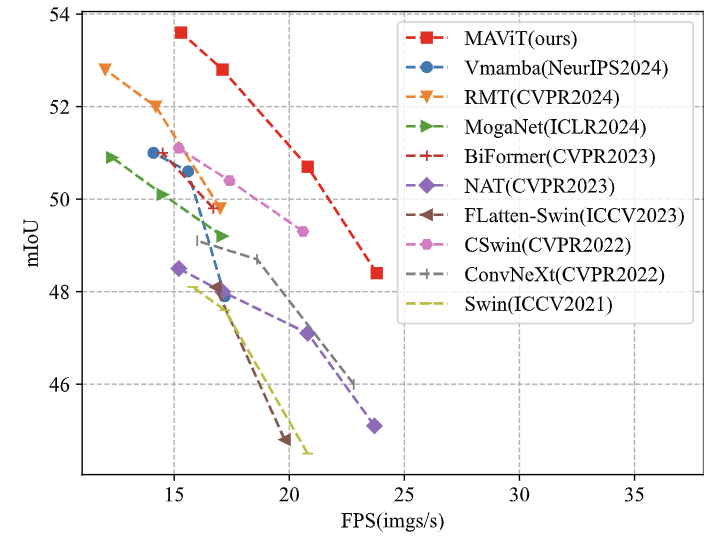
如图 9 所示，MAViT 在各种大小上都优于其他模型。具体来说，MAViT-B 在 UperNet 框架下实现了 52.8 mIoU，超过了更大的 MILA。MAViT-L甚至可以达到 53.6 mIoU。

推理效率

图 10 展示了不同模型在低分辨率任务上的推理效率，其中 MAViT 在吞吐量和准确性之间取得了最佳平衡。同样，对于高分辨率任务，图 11 中的结果进一步突出了 MAViT 的卓越性能。这表明 MALA 不仅的理论复杂度明显低于 Softmax Attention，而且在实践中也实现了较高的推理速度。

语言模型实验

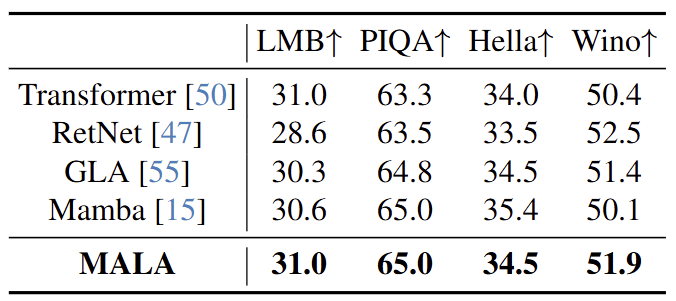
作者基于 15B token 训练了 0.3B MALA 模型，并在几个常用的基准上评估模型。结果如图 12 所示，在四种常用的基准 (LMB、PIQA、Hella 和 Wino) 中，MALA 表现出强大的性能。

生成模型实验

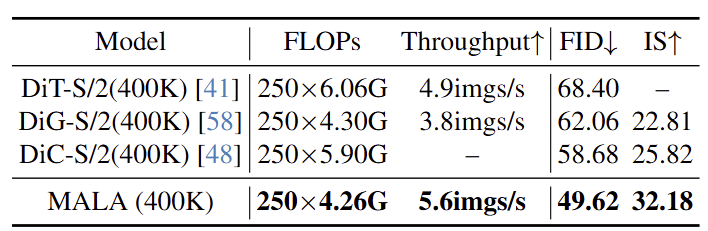
结果如图 13 所示，与基于 ConvNet 或者 Transformer 的其他方法相比，基于 MALA 的模型表现出更好的性能和更快的速度，证明了 MALA 的优越性。

参考

1. Efficientvit: Lightweight multi-scale attention for highresolution dense prediction
2. Flatten transformer: Vision transformer using focused linear attention