
AIxiv专栏是机器之心发布学术、技术内容的栏目。过去数年,机器之心AIxiv专栏接收报道了2000多篇内容,覆盖全球各大高校与企业的顶级实验室,有效促进了学术交流与传播。如果您有优秀的工作想要分享,欢迎投稿或者联系报道。投稿邮箱:liyazhou@jiqizhixin.com;zhaoyunfeng@jiqizhixin.com
陈枳扦博士:现任密西西比州立大学计算机系助理教授,专注于图机器学习及应用领域,在谱域视角与不确定性研究方面着力颇深。其研究成果见诸于 AAAI、IJCAI、ACM、ICDM、EMNLP、Computing Surveys、Nature Communication 等。他的科研工作承蒙美国国家科学基金会(NSF)及美国农业部(USDA)多个项目的资助,且荣获丰田研究院杰出贡献奖与 ACM SIGPSATIAL 2020 最佳论文奖。
张磊博士:于 2024 年毕业于弗吉尼亚理工后,以助理教授身份加盟北伊利诺伊大学。他的研究兴趣广泛覆盖机器学习和数据挖掘范畴,尤其聚焦于图神经网络、图结构学习、双层优化、神经架构搜索以及社交网络挖掘等方面。在 AAAI、ICDM 等顶级会议上发表多篇论文,并于 2023 年夏季斩获弗吉尼亚理工大学的 Cunningham Fellowship。
赵亮博士:身为埃默里大学计算机系副教授,他的研究领域横跨数据挖掘、人工智能等多学科,在图学习领域成果斐然。在 KDD、NeurIPS、AAAI、IJCAI、WWW 等众多顶级会议及期刊上发表超百篇论文,屡获殊荣,如 NSF CAREER 奖、Meta Research 奖、Amazon Research 奖等,还荣获 ICDM 2022 最佳论文奖、ACM SIGPSATIAL 2022 最佳论文奖以及 WWW 2023 最佳论文提名等。
图数据学习在过去几年中取得了显著的进展,图神经网络(GNN)在此过程中起到了核心作用。然而,不同的 GNN 方法在概念和实现上的差异,对理解和应用图学习算法构成了挑战。
针对这一问题,来自密西西比州立大学,北伊利诺伊大学和埃默里大学的学者通过一系列教程对此问题展开了讨论,这些教程展示在 CVPR 2024、CIKM 2024、SIAM Math and Data Science 2024,以及发表在 Computing Surveys 的一篇论文: 《Bridging the Gap between Spatial and Spectral Domains: A Unified Framework for Graph Neural Networks》。

论文地址:https://dl.acm.org/doi/10.1145/3627816
问题:统一框架的突破意义何在?
尽管图神经网络已经在多个领域展示出了卓越的性能,从化学分子识别到社交网络分析,从交通网络到输电网络,再到大脑网络。GNN 也在不同的场景下,用不同的理论和机制来设计新的图神经网络,例如 Heat diffusion, page rank, random walk, attention model, ARMA, low-pass filtering。虽然展现了 GNN 和很多不同理论工具的连接性,但这也加剧了 GNN 领域的分裂。这些方法因为急于不同理论,无法进行理论上直接的比较。

Part 1: 图学习理论框架的现状
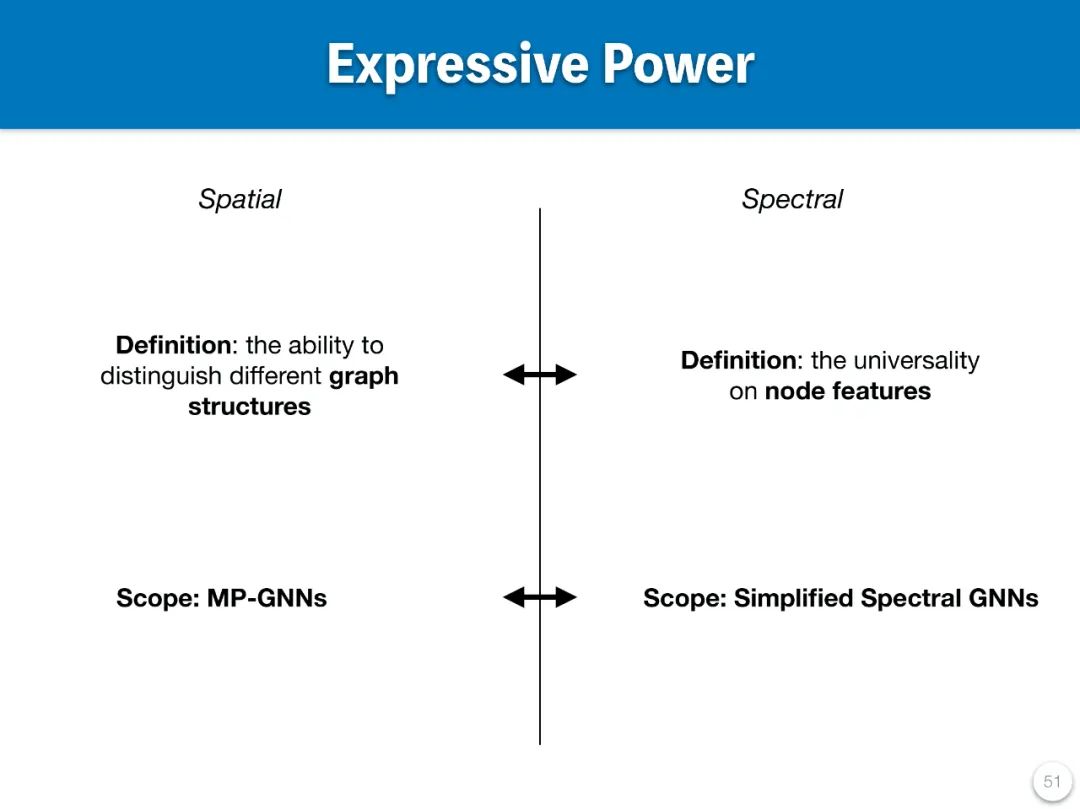
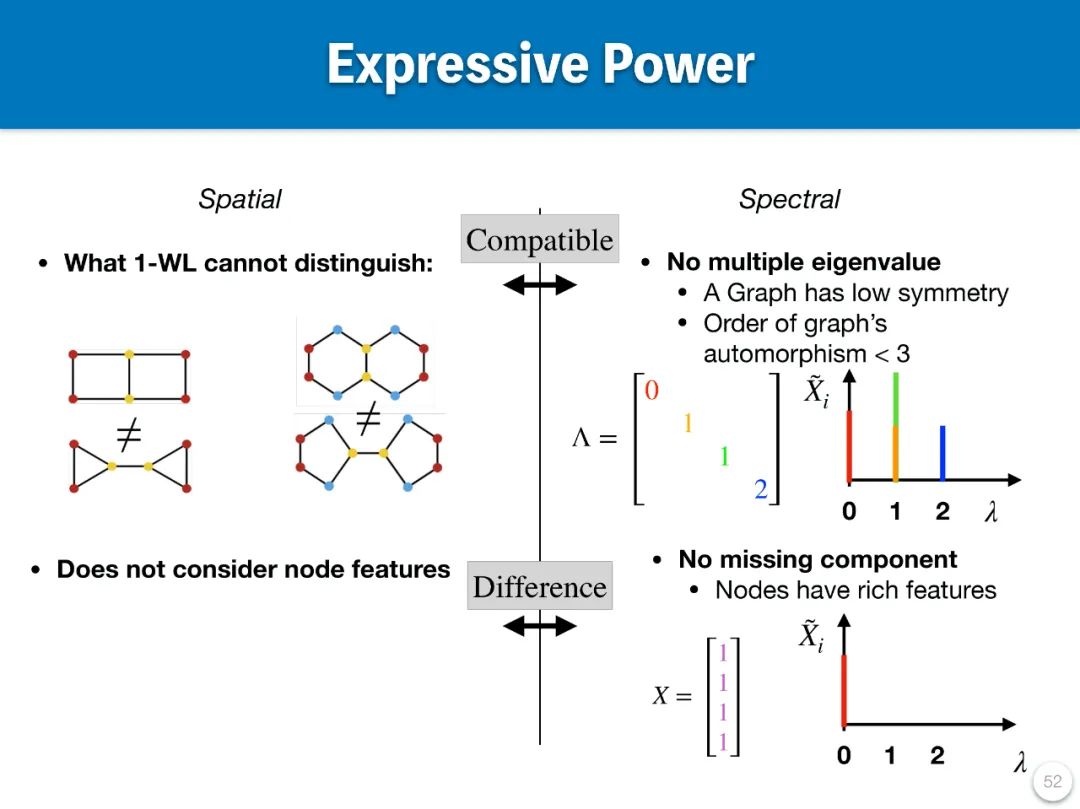
目前,图神经网络(GNN)涵盖了多种模型和层的类型,但总体可以分为空域(spatial)图模型和频域(spectral)图模型。针对这些模型,不少研究者尝试提出通用框架,以便在同一框架下对不同模型进行分析和比较。然而,这些框架主要集中于空域图模型。值得注意的是,有一类研究从统一的出发点 —— 即模型的表达能力(Expressive Power)—— 对空域和频域图模型进行了分析。尽管如此,空域和频域图模型在表达能力的定义上存在差异,其分析结论和设计建议既有共通之处,也各有不同,同时两者均存在一定的局限性。
Part 2: 图卷积
图卷积可以通过谱图理论(Spectral Graph Theory)中的图傅里叶变换(Graph Fourier Transform)和卷积定理(Convolution Theorem)来理解。
图傅立叶变换:图的结构通过图拉普拉斯矩阵(Graph Laplacian)来表示。拉普拉斯矩阵 L 可以进行特征值分解: ,其中 U 是特征向量矩阵,∧ 是特征值的对角矩阵。图傅里叶变换就是将图信号
,其中 U 是特征向量矩阵,∧ 是特征值的对角矩阵。图傅里叶变换就是将图信号 转换到频域:
转换到频域: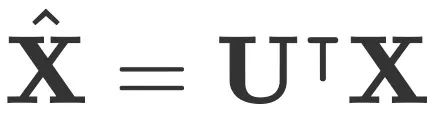 。其逆变换为
。其逆变换为 。通过这种变换,研究者可以在频域中处理和分析图信号。
。通过这种变换,研究者可以在频域中处理和分析图信号。
卷积定理:在传统信号处理中,时域的卷积等价于频域的逐点相乘。对于图信号,同样成立:设两个图信号 X(输入特征)和 g(滤波器),它们的图卷积定义为: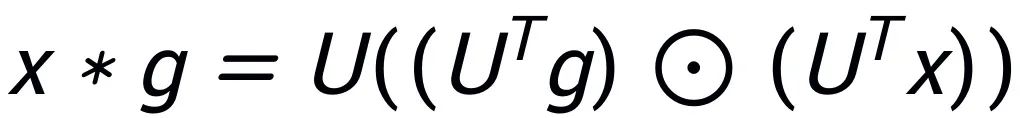 。其中,⊙ 表示频域的逐点相乘,g 表示频域滤波器。这表明图卷积可以通过频域操作实现。为了在图神经网络中实现卷积,滤波器 g 被参数化为
。其中,⊙ 表示频域的逐点相乘,g 表示频域滤波器。这表明图卷积可以通过频域操作实现。为了在图神经网络中实现卷积,滤波器 g 被参数化为 ,它是特征值 ∧ 的函数:
,它是特征值 ∧ 的函数: ,其中 θ 是可训练的参数向量。卷积操作可以写为:
,其中 θ 是可训练的参数向量。卷积操作可以写为: 。
。
图卷积网络(GCN)在频域和空域的解释:在频域图模型中,GCN 使用的是 的一阶近似,其中
的一阶近似,其中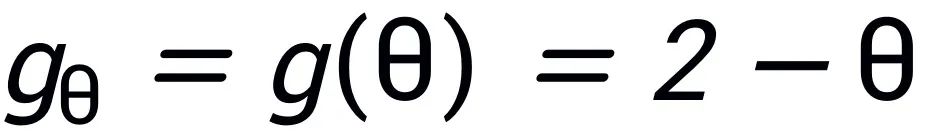 。这种操作本质上是一种固定的卷积操作,没有可学习参数。由于归一化之后的拉普拉斯矩阵的特征值范围为 0 到 2 之间,2-θ 的滤波器实际上是一个低通滤波器:放大低频平滑信号,减弱高频信号。在空域图模型中, GCN 的操作可以理解为对每个节点的邻居节点的特征值进行求和,然后取平均值。这是一种基于邻居特征聚合的方式。GCN 的频域和空域视角是等价的,但各有侧重。频域解释更偏向理论上的信号处理本质,而空域解释更贴近工程实现和直观理解。对于研究者而言,这两种视角是相辅相成的,结合使用可以更全面地理解和改进 GCN。
。这种操作本质上是一种固定的卷积操作,没有可学习参数。由于归一化之后的拉普拉斯矩阵的特征值范围为 0 到 2 之间,2-θ 的滤波器实际上是一个低通滤波器:放大低频平滑信号,减弱高频信号。在空域图模型中, GCN 的操作可以理解为对每个节点的邻居节点的特征值进行求和,然后取平均值。这是一种基于邻居特征聚合的方式。GCN 的频域和空域视角是等价的,但各有侧重。频域解释更偏向理论上的信号处理本质,而空域解释更贴近工程实现和直观理解。对于研究者而言,这两种视角是相辅相成的,结合使用可以更全面地理解和改进 GCN。
Part 3: 新的统一框架:连接空域和频域
教程中提出的框架基于一个核心假设:空间域和频谱域的图表示学习可以通过一个共同的数学语言进行描述。研究人员引入了一种新的图嵌入方法,该方法结合了图的空间连接性和节点特征,能够更加精准地捕捉和表示图数据的复杂性。

其他领域里频域和空域的研究
在已存在的研究里,这种空域和频域相互连接视角并不少见。研究者用两个例子来说明:
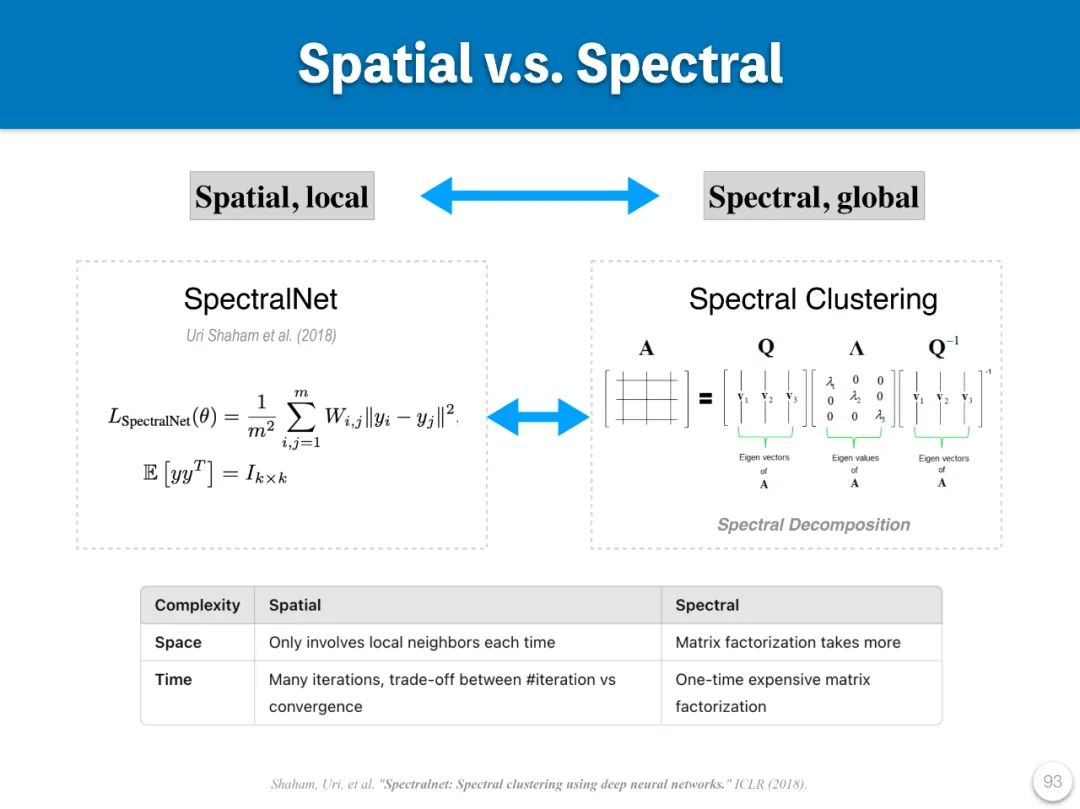
(1)谱聚类:从谱域的视角看谱聚类是使用谱分解 (spectral decomposition) 或则说特征分解(eigen-decomposition),然后使用分解结果中特征值响亮的低频信号来作为新的表达,然后使用较为简单快速的 Kmeans 得到聚类结果。而另外一个新的实现,SpectralNet,设计了一个特别 loss,使用神经网络来得到几乎一样的结果。单神经网络是一种以降低 loss 为导向的迭代算法,所以可以视为一种近似谱聚类的算法。
(2)另外一个例子是著名的 Word2Vec 算法。以 Skip-gram 为例,每个单词都要相似于它的上下文的环境里其他单词。所以 Word2Vec 是一个迭代算法。在后来的研究中,Levy 提出了一些分析,发现使用 Word2Vec 的结果里的矩阵,能够几乎完整的还原单词的共现矩阵(PPMI)。也就是说 Word2Vec 可以看作是矩阵分解算法的一种近似算法。

在这两个例子中,研究者发现这种比较中,有类似于该研究提出的谱域和空域方法区别。即,一种方法侧重矩阵分解,而另外一种侧重于迭代近似。
Part 4: 未来方向展望
这项研究开辟了图结构学习领域的新方向,未来的研究可以基于此框架进一步探索:
-
计算效率:如何进一步优化统一框架以处理大规模图数据,在谱论表达下,图的信息量依然巨大,对计算仍然是一个挑战。
-
统一的谱论:目前谱论主要应用于静态图结构,而且是简单图(即无向,边只连接两个节点)。然后图论中仍然有大量的不同类型的图,缺少谱论的表达,例如有向图,超图,或则动态图。
-
应用扩展:将统一框架应用到更多实际问题中,如生物信息学和社会网络分析,如何解释谱论视角下真实应用的规律,是一个值得探索的领域。
(文:机器之心)
