
极市导读
本文为 Transformer 的 FFN 和 Attention 的投影层开发了一个 Int8 矩阵乘法,在保持全精度性能的同时将推理所需的 GPU Memory 减少了一半。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
太长不看版
大语言模型量化初探。
Weight:Per-channel,Activation:Per-token
本文 LLM.int8() (https://arxiv.org/pdf/2208.07339) 比 SmoothQuant (https://arxiv.org/pdf/2211.10438) 更早,属于是 LLM 量化早期开荒的工作之一。LLM 被广泛采用,但也需要大量 GPU Memory 做推理。
本文为 Transformer 的 FFN 和 Attention 的投影层开发了一个 Int8 矩阵乘法,在保持全精度性能的同时将推理所需的 GPU Memory 减少了一半。使用我们的方法,可以随时加载 175B 参数模型的 16/32-bit Checkpoint,转换为 Int8,随时使用而不会导致性能下降。本文方法理解并处理了 Transformer 中存在的异常值特征 (Outlier Feature),这些特征主导了 Transformer 的性能。
为了处理这些特征,本文提出了一个两步量化方法 LLM.int8()。首先,使用 vector-wise quantization (对矩阵乘法中的每个内积单独设置归一化常数) 量化大部分特征。然后就是一种新的混合精度分解的方案,将异常值特征做 16-bit 矩阵乘法。同时,超过 99.9% 的其他正常特征仍做 8-bit 矩阵乘法。使用 LLM.int8() 之后,可以最多执行 175B 参数模型的推理,而且没有任何性能下降。
专栏目录
https://zhuanlan.zhihu.com/p/687092760
本文目录
1 LLM.int8():大语言模型 8-bit 量化初探
(来自 University of Washington, Facebook AI Research)
1 LLM.int8() 论文解读
1.1 LLM.int8() 研究背景
1.2 8-bit 数据类型以及量化
1.3 LLM.int8() 贡献1:Vector-wise Quantization
1.4 LLM.int8() 贡献2:混合精度分解
1.5 实验设置
1.6 主要结果
1.7 Transformer 中的异常值特征分析
1 LLM.int8():大语言模型 8-bit 量化初探
论文名称:LLM.int8(): 8-bit Matrix Multiplication for Transformers at Scale (NeuIPS 2022)
论文地址:
http://arxiv.org/pdf/2208.07339
1.1 LLM.int8() 研究背景
对于参数超过 6.7B 的 LLM 而言,FFN 和 Attention 的投影层及其矩阵乘法操作占所有参数量的 95%,计算量的 65-85%。减少参数尺寸的方法之一是将其量化为更低比特的数据,并使用低比特精度来做矩阵乘法。基于这一点,已经开发了 8-bit Transformer 的量化方法。这些方法虽然减少了显存的占用,但它们会降低性能,通常需要在训练期间进一步调整量化,并且仅针对参数少于 350M 的模型。数十亿参数模型量化仍是一个开放的挑战。
本文提出了第一个十亿规模 Transformer 模型的 Int8 量化过程,且不会带来任何性能下降。该方法使得加载 16、32-bit 的 175B 参数的 Transformer 成为可能,将 FFN 和 Attention 的投影层转换为 8-bit,并立刻使用量化的结果进行推理,不会产生任何精度下降。本文通过解决两个关键挑战来实现这一点:
-
需要在超过 1B 参数量的模型上获得更高的量化精度。 -
需要解决异常值特征的问题,这个问题会破坏量化精度,尤其是超过 6.7B 参数量级的模型。破坏量化精度的具体表现就是 C4 evaluation perplexity 和 zeroshot 精度下降。
通过本文提出的第一个方法,vector-wise quantization,可以在高达2.7B参数的尺度上保持性能。对于向量量化,矩阵乘法可以看作是行和列向量的独立内积序列。因此,可以对每个内积使用单独的归一化常数来提高量化精度。可以在执行下一个操作之前,通过列和行归一化常数的外积进行去归一化操作,来恢复矩阵乘法的输出。
为了在没有性能下降的情况下扩展到 6.7B 参数以上,了解推理过程中特征维度出现的异常值至关重要。为此,本文进行了一个分析,表明异常值特征 (幅值大于其他通道) 会首先出现在 Transformer 层大约 25% 中。随着缩放 Transformer 到 6B 参数,逐渐扩散到其它层。在 6.7B 参数量级左右,所有 Transformer 层,以及超过 75% 的序列 token 都受到异常值特征的影响。这些异常值是高度系统的:在 6.7B 的模型规模上,每个序列出现大约 150,000 个异常值,但仅集中在整个 Transformer 的 6 个特征维度中。将这些异常值特征设置为 0 会使 top-1 attention softmax 概率质量降低 20% 以上,将验证困惑度降低 600-1000%,尽管异常值特征仅占所有输入特征的约 0.1%。相比之下,删除相同数量的随机特征会使概率降低 0.3%,困惑度仅仅会降低约 0.1%。
为了支持具有这种极端异常值的量化,作者开发了混合精度分解,对异常值特征维度执行 16-bit 矩阵乘法,对其他 99.9% 的维度执行 8-bit 矩阵乘法。作者将矢量量化和混合精度分解的组合称为 LLM.int8()。通过使用 LLM.int8(),可以在 LLM 中执行最多 175B 参数模型的推理,且不会有任何性能下降。本文方法不仅为这些异常值对模型性能的影响提供了新的见解,而且首次使得在消费者 GPU 的单个服务器上使用大模型 (例如 OPT-175B/BLOOM) 成为可能。
1.2 8-bit 数据类型以及量化
本文对两个问题感兴趣:模型缩放到什么规模量化会失败?为什么会失败?以及这怎么与量化精度相关?
为了回答这些问题,我们研究了高精度非对称量化 (Zeropoint quantization) 和对称量化 (Absmax quantization)。虽然 Zeropoint 量化通过使用数据类型的全位范围来提供高精度,但由于实际的限制,它很少使用。Absmax 量化是最常用的技术。
Absmax 量化
Absmax 量化把输入 scale 到 8-bit 范围 , 方法是通过乘以 , 其计算方法是用 127 除以整个张量的绝对最大值。因此,对于 FP16 输入矩阵 的 Absmax 量化由下式给出:
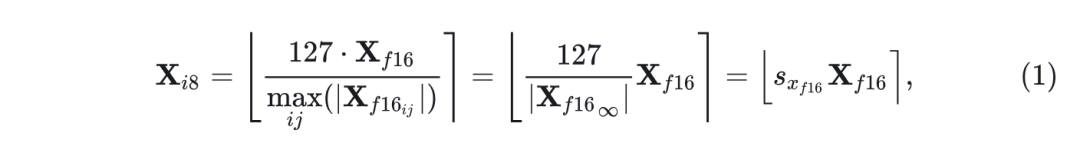
其中, 表示四舍五入到最接近的整数。
Zeropoint 量化
Zeropoint 量化通过使用归一化动态范围 把输入 scale 到 8-bit 范围 [−127, 127],然后通过零点 移动。通过这种仿射变换,任何输入张量都将使用数据类型的所有位,从而减少非对称分布量化误差。
比如对于 ReLU 输出,在 Absmax 量化中,[−127, 0) 中的所有值都未使用,很浪费量化精度。而在 Zeropoint 量化中,使用了完整的 [−127, 127] 范围。Zeropoint 量化由以下方程给出:

为了在操作中使用 Zeropoint 量化,将Zeropoint 加到张量 的每个元素。例如,为了将两个零点量化数字 和 及其零点 和 相乘,计算:
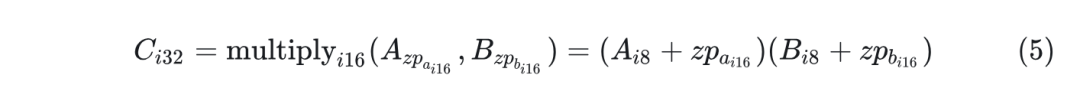
如果 指令不可用在 GPU 或 TPU 上,就需要展开:
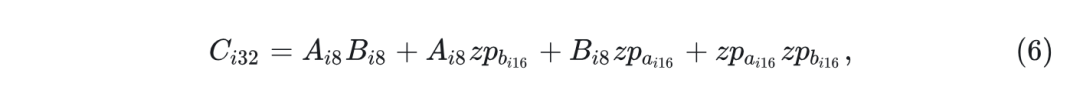
其中, 使用 Int8 精度计算,其余以 Int16/32 精度计算。因此,如果 指令不可用,Zeropoint 量化可能会很慢。在这两种情况下,输出都累积为一个 32-bit 整数 。为了去量化 ,除以缩放常数 和 。
Int8 矩阵乘法与 FP16 输入和输出
给定隐藏状态 和权重为 ,序列长度 、特征维度 和输出维度 ,使用 16 位输入和输出执行 8 位矩阵乘法,如下所示:
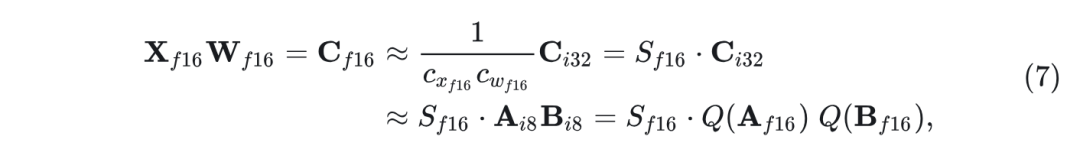
其中, 是 Absmax 或 Zeropoint 量化, 和 分别是 scaling 常数,对于 Absmax 量化是 和 ,对于 Zeropoint 量化是 和 。
1.3 LLM.int8() 贡献1:Vector-wise Quantization
为每个 tensor 使用一个 scaling 常数的量化方法的主要挑战是:一个异常值就降低该 tensor 中所有其他数值的量化精度。因此,希望每个张量有多个 scaling 常数。因此,作者使用了 Vector-wise Quantization。
为了处理参数规模在 6.7B 之上的所有 Transformer 中出现的大幅度异常值特征,Vector-wise Quantization 也不够了。为此,本文开发了混合精度分解,将少量大幅值的特征维度 (≈0.1%) 以 16-bit 精度表示,而其他 99.9% 的正常值进行 8-bit 运算。由于大多数的值仍然以低比特表示,因此与 16-bit 相比,降低了大约 50% 的显存。例如,对于 BLOOM-176B,将模型的显存占用减少了 1.96 倍。
Vector-wise Quantization 和混合精度分解如图 2 所示。LLM.int8() 方法是 Absmax Vector-wise 量化和混合精度分解的组合。
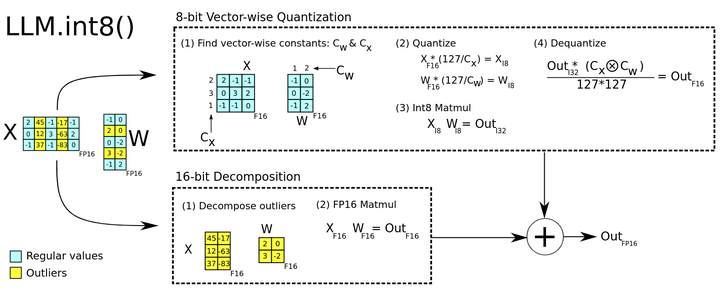
增加矩阵乘法 scaling 常数的数量的方法之一是将矩阵乘法视为是独立的内积。给定隐藏状态 和权重 ,可以将不同的 scaling 常数 分配给 的每一行, 将不同的 scaling 常数 分配给 的每一列。为了反量化, 将每个内积结果重新做归一化,乘以 。对于整个矩阵乘法,这相当于使用外积 进行去归一化, 其中 。因此, 矩阵乘法的完整方程由下式给出:
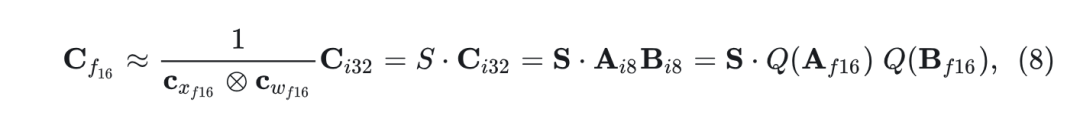
上式作者称之为矩阵乘法的 Vector-wise Quantization。
1.4 LLM.int8() 贡献2:混合精度分解
参数规模达到十亿级的 8-bit Transformer 的一个重要问题是,它们具有异常值特征,需要高精度的量化。然而, Vector-wise Quantization,即量化隐藏状态的每一行,对异常值特征无效。幸运的是,可以观察到这些异常值特征在实践中既非常稀疏又系统,仅占所有特征维度的 0.1%。因此,作者开发了一种新的混合精度分解技术。
作者发现,给定输入矩阵 ,这些异常值系统地出现在几乎所有序列维度 中,但仅出现在特定的特征维度 中。因此,作者提出了矩阵乘法的混合精度分解,将异常值特征维度分成集合 ,其中包含至少有一个异常值大于阈值 的所有特征维度 。作者发现 足以使得 Transformer 性能下降接近 0。矩阵乘法混合精度分解的定义如下:
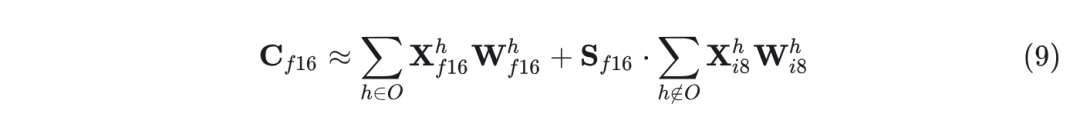
其中, 是 Int8 输入和权重矩阵 和 的去归一化项。
这种分解对于超过 99.9% 的值使用 8-bit 高效的矩阵乘法,对异常值使用 16-bit 高精度乘法。由于高达 13B 参数的变压器的异常特征维度的数量不大于 7 ( ),因此这种分解操作仅消耗大约 0.1% 的额外的显存。
1.5 实验设置
作者测量量化方法的鲁棒性,将几个公开可用的预训练语言模型的大小扩展到 175B 参数。关键问题不是量化方法对特定模型的表现如何,而是随着我们规模,本文方法的表现趋势。
作者使用了两种设置。一种基于语言建模的困惑度,作者发现这是一种对量化退化非常敏感的度量,并使用此设置来比较不同的量化 baselines。此外,作者评估了一系列不同最终任务的 OPT 模型的 Zero-shot 精度下降,并将本文方法与 16 位 baseline 进行比较。
对于语言建模设置,使用 fairseq 中预训练的 autoregressive transformers,参数范围从 125M 到 13B。这些模型已经在 Books,English Wikipedia, CC-News,OpenWebText,CC-Stories,English CC100 上做了预训练。
为了评估 Int8 量化的语言建模退化,作者评估了 8-bit 模型在 C4 corpus 的验证数据集上的困惑度,这是 Common Crawl 语料库的一个子集。
为了衡量 Zero-shot 的性能下降,作者使用 OPT 模型,并在 EleutherAI 语言模型评估工具上评估。
1.6 主要结果
在 C4 corpus 上评估的 125M 到 13B Int8 模型的语言建模困惑度结果如图 3 所示。可以看到,Absmax、逐行和 Zeropoint 量化随着模型的缩放失败了,其中 2.7B 参数之上的模型效果比小模型的效果差很多。只有 LLM.int8() 可以很好地保留困惑度。
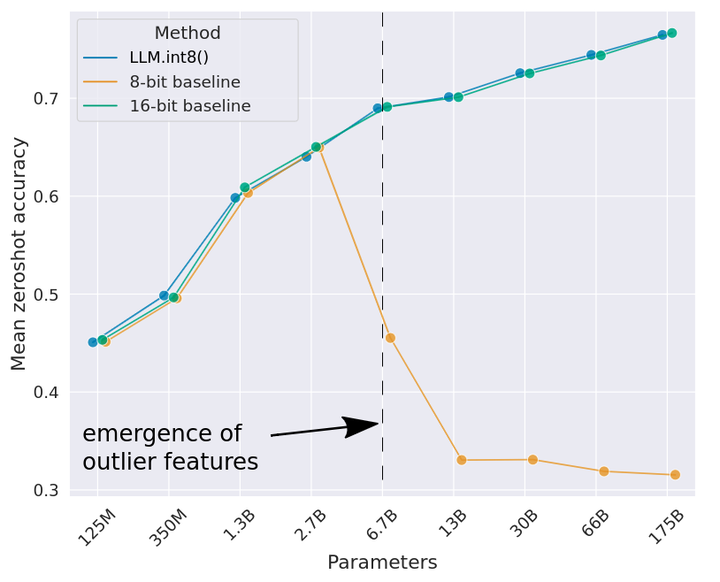
如图 1 所示,当查看 OPT 模型的 Zero-shot 性能的扩展趋势时,可以看到 LLM.int8() 当把参数量从 125M 扩展到 175B 时,保持了完整的 16-bit 的性能。另一方面,8-bit Absmax vector-wise 量化,缩放性能很差并最终性能完全退化为随机。
虽然本文的主要重点是节省显存,但作者也测量了LLM.int8() 的运行时间。与 FP16 baseline 相比,对于参数量小于 6.7B 的模型,量化会减慢推理速度带来额外的开销。然而,6.7B 参数或者更小的模型完全适合大多数 GPU,在实践中很少需要量化。在 175B 模型中,LLM.int8() 运行时间对于相比于大矩阵乘法快大约两倍。
1.7 Transformer 中的异常值特征分析
当我们缩放 Transformer 时, 大幅度的异常值特征会出现并强烈地影响所有层以及量化过程。给定一个隐藏状态 ,其中 是 token 维度, 是特征维度,将特征定义为特定维度 。作者分析查看给定 Transformer 所有层的特定维度 。
作者发现异常值特征强烈影响 Attention 和 Transformer 的整体性能。虽然对 13B 模型每 2048 个 token 序列存在多达 150k 个异常值,但这些异常值特征是高度系统的,只有最多 7 个特征维度 。这个见解对于开发混合精度分解至关重要。本文的分析解释了 Zeropoint 量化的优点,以及为什么使用混合精度分解之后这个优势会消失。
找到异常值特征
作者根据以下标准定义异常值:特征的大小至少为 6.0,影响至少 25% 的层,并影响至少 6% 的序列。
给定一个具有 层的转换器和隐藏状态 , 其中 是序列维度, 是特征维度。作者追踪这样的特征维度 , 其至少有一个值大小大于等于 6 , 且这些异常值出现在至少 的层中,以及所有序列维度的至少 中。
作者发现,使用混合精度分解之后,如果将大于 6 的特征作为异常值特征,困惑度退化就会停止。对于受异常值影响的层数,作者发现异常值特征在大型模型中是系统性的:要么出现在大多数层中,要么不出现。但是,在小型模型中是概率性的:对于每个序列,有时出现在某些层中。
测量异常值特征的影响
为了证明异常值特征对 Attention 和预测性能至关重要,作者隐藏状态 输入注意力投影层之前将异常值特征设置为 0,然后比较 top-1 softmax 概率与常规 softmax 概率。作者独立地对所有层执行此操作。作者删除了异常值特征维度 (将其设置为0) ,并继续使 Transformer 前向传播这些改变的隐藏状态,并报告了这么做的困惑度退化。作为控制变量,也对随机非异常值特征维度应用相同过程,并报告注意力和困惑度退化。主要结果概括为 4 点:
-
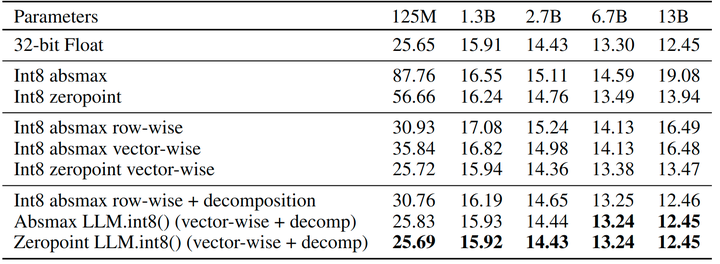
当使用参数量测量时,所有层的异常值特征的出现,突然发生在 6B 和 6.7B 参数之间,如图 5(a) 所示。受到异常值影响的层的数量百分比从 65% 增加到 100%,受到异常值影响的 token 的数量百分比从 35% 增加到 75%。同时,量化开始失败。 -
当使用困惑度测量时,异常值特征的出现随困惑度的变化可以视为一种指数函数,如图 5(b) 所示。这表明异常值特征的出现不仅有关模型大小,还涉及困惑度,与所使用的训练数据量和数据质量等多个附加因素有关。 -
如图 6(a) 所示,一旦 Transformer 所有层中出现异常值特征,其中位数数值的大小会迅速增加。异常值特征及其非对称分布破坏了 Int8 量化精度。这是量化方法从 6.7B 参数规模开始失败的核心原因:数据分布的范围太大,使得大多数 quantization bins 是空的,小的量化值被量化为零,基本上消除了信息。作者假设除了 Int8 推理之外,由于 6.7B 及以上模型的异常值,常规 16-bit 浮点训练变得不稳定:如果值为 60 的向量相乘,很容易偶然超过最大 16-bit 数值 65535。 -
如图 6(b) 所示,异常值特征的数量随 C4 困惑度单调增加,但与模型大小的关系不是单调的。这表明决定相移的是模型困惑度,而非模型大小。
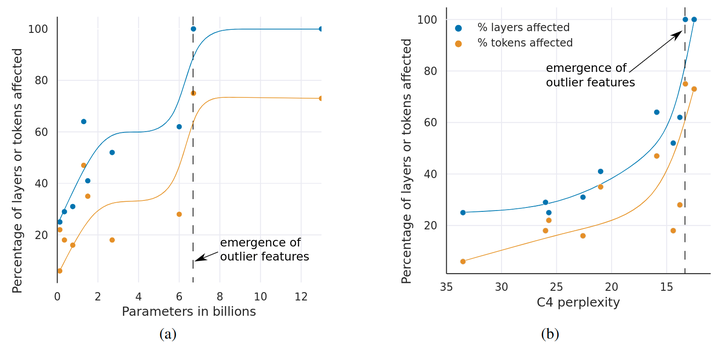
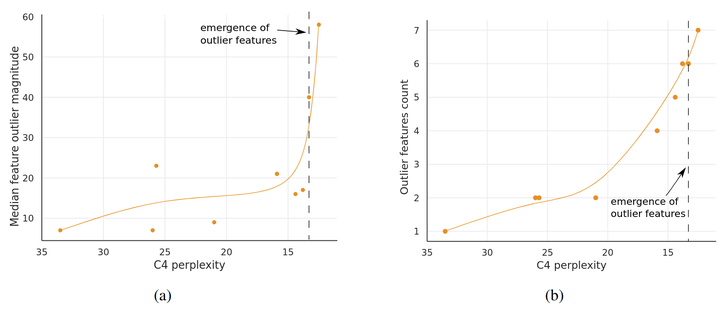
异常值特征是高度系统的。例如,对于序列长度为 2048 的 6.7B 模型,每个序列在整个模型中找到大约 150k 个异常值特征,但它们仅集中在 6 个不同的特征维度中。
这些异常值对于 Transformer 性能至关重要。如果去除异常值,即使最多有 7 个异常值特征维度,top-1 softmax 概率从约 40% 降低到约 20%,验证集困惑度增加了 600-1000%。当改为删除 7 个随机特征维度时,top-1 概率仅下降 0.02-0.3%,困惑度增加 0.1%。这些结果突出了异常值特征的关键性质。这些异常值特征的量化精度至关重要,因为即使是微小的误差也会极大地影响模型性能。
量化性能的解释
本文的分析表明,特定维度中的异常值存在于较大模型中,并且这些特征维度对于 Transformer 性能至关重要。由于逐行和矢量量化缩放每个隐藏状态序列维度 ,由于异常值出现在特征维度 中,这两种方法都不能有效地处理这些异常值。这就是为什么 Absmax 量化方法在异常值出现后很快失败的原因。
但是,几乎所有的异常值都是严格的非对称分布:要么完全是正的,要么是负的。这就使得 Zeropoint 量化对这些异常值特别有效,因为 Zeropoint 量化是一种非对称量化方法,将这些异常值缩放到完整的 [−127,127] 范围内。这解释了图 4 中的强大性能。然而,在 13B 规模尺度上,即使是 Zeropoint 量化也由于累积的量化误差和异常值大小的快速增长而失败,如图 6(a) 所示。
如果使用具有混合精度分解的完整 LLM.int8()方法,Zeropoint 量化的优势消失,表明剩余的特征是对称的。然而,Vector-wise 量化仍然比逐行量化有优势,表明需要增强模型权重的量化精度来保持全精度性能。

(文:极市干货)
