©PaperWeekly 原创 · 作者 | 吕俊良
本文介绍了中国人民大学统计学院的一篇关于多任务贝叶斯联邦学习的文章“Task Diversity in Bayesian Federated Learning: Simultaneous Processing of Classification and Regression”,本文被 KDD 2025 接收,代码已经开源。

Task Diversity in Bayesian Federated Learning: Simultaneous Processing of Classification and Regression
论文链接:
https://doi.org/10.48550/arXiv.2412.10897
代码链接:
https://github.com/JunliangLv/task_diversity_BFL

背景
近些年来,边缘设备(edge devices)和物联网设备(Internet of Things devices)的激增引发了对分布式算法的强烈需求。联邦学习(federated learning,FL)使用分散在多个局部设备上的数据进行训练,避免大规模数据传输,从而增强局部隐私。
然而,现有的联邦学习工作集中于处理同质性任务,即只使用每台局部设备的数据进行分类任务训练,或只进行回归任务训练。这与现实情况中每台设备的数据可用于多种训练任务不符。
以健康监测设备为例,其收集的步频、心率、睡眠情况等传感器数据既可用于运动状态分析(分类任务),也可用于健康状况评估与预测(回归任务)。因此,有必要将多任务学习(multi-task learning,MTL)与联邦学习结合,处理局部设备中的多样性任务。
另一方面,贝叶斯联邦学习(Bayesian federated learning,BFL)通过对参数引入合适的先验分布作为正则项,缓解了有限数据下的过拟合,同时得到不确定性的估计。BFL 的优势使其在风险决策、样本外(out-of-distribution)检测等方面表现出竞争力。

方法
本文的核心思路是使用概率模型,将局部水平下的多任务学习与全局水平下的联邦学习结合。
具体而言,在局部设备中,基于给定的先验分布,多输出高斯过程(multi-output Gaussian processes,MOGP)被用于联合建模多个相关的分类和回归任务并得出后验分布;在全局处理器中,来自不同设备的后验分布被上传聚合得到更新的全局 MOGP 先验,再分发回局部设备进行下一轮训练。
值得注意的是,由于分类似然函数与 MOGP 先验非共轭,直接在局部设备执行后验推断不可行。为解决这一挑战,本文采用 Polya-Gamma 数据增强技术将非共轭问题转化为共轭问题,并通过 mean-field 变分推断得到后验分布的闭式解。
文献中指出在条件共轭模型中执行 mean-field 变分推断等价于使用步长为 1 的自然梯度下降优化似然函数的证据下界。这种近似二阶优化算法相比于传统的一阶方法展现出更快的收敛速度。
为了进一步增强 MOGP 的建模效果,作者使用深度核技术(deep neural network)。深度核通过神经网络将输入数据转化为潜在表示,再将其作为传统核函数的输入。
不同于依赖欧氏距离的传统核方法,深度核方法以数据驱动的方式实现了更为灵活的数据转换。同时,为增强局部样本量较大时的计算效率,作者介绍了诱导点技术(inducing points),将局部设备中立方计算复杂度降低为线性计算复杂度,并给出带有诱导点的 mean-field 变分推断方法的显式后验分布。


实验
1. 准确性
下图展现了本文提出的多任务学习方法,pFed-Mul,在模拟数据集中成功拟合真实值。与单任务模型相比,pFed-Mul 不仅提高了拟合的精度,而且降低了预测不确定性。

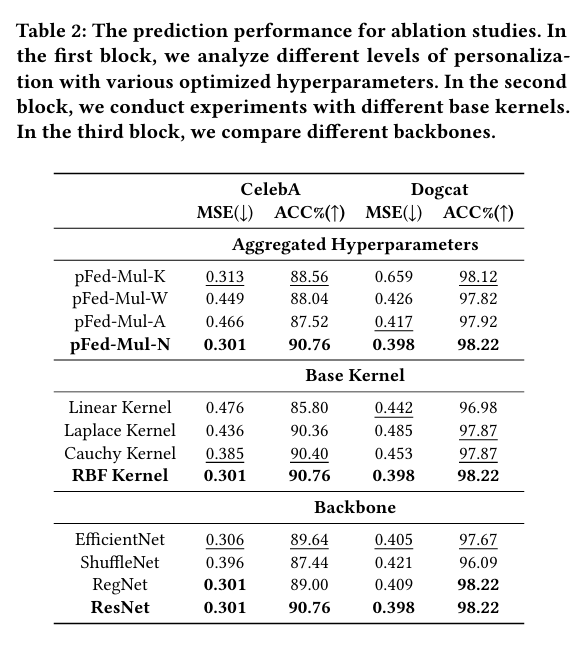
下表报告了在三种小样本学习情境下,评估模型在分类任务上的准确率和在回归任务上的均方误差。与基线模型相比,pFed-Mul 在脸部特征数据集 CelebA 和增强的猫狗分类数据集均取得较好的效果。其中针对回归任务,最显著的改进为提高均方误差 0.155;针对分类任务,最显著的改进为提高准确率 3.86%。

这表明局部设备上的多任务交互既可以扩大训练数据量,缓解过拟合,增强全局模型的鲁棒性;又可以通过任务之间的相关性,迁移先验知识,从而增强收敛效率。
本文通过模型校准和 OOD 检测两个视角说明 pFed-Mul 相比于基线模型提供了更好的不确定性估计。
下图展示了模型在 CelebA 数据集上的分类任务校准效果。作者使用可靠性图展示了模型校准结果与完美校准之间的差距,并通过期望校准误差(expected calibration error,ECE)量化比较校准效果。pFed-Mul 展示出最佳的校准结果,并取得最低的 ECE。

为说明 OOD 检测的效果,作者选取一系列测试图片,随机遮盖其中两张图片,并计算对应的分类预测方差。下图说明 OOD 样本展现出更大的预测方差。这表明 pFed-Mul 不仅能提供预测结果用作决策参考,还可以输出预测不确定性用作风险度量。

3. 收敛速度
作者比较了 pFed-Mul 和其他基线模型的收敛速度,并在下图展示前 10 次全局迭代中分类任务的准确率。pFed-Mul 不仅展现出领先的收敛速率,而且在训练过程中保持稳定的表现,在 10 次全局迭代后取得最佳的分类效果。
这一结果从数值上验证了对 Polya-Gamma 数据增强的 MOGP 模型执行 mean-field 变分推断的更优收敛速率。

作者执行多种消融实验评估模型各部分的重要性,包括参数聚合的程度、核函数选择和底层神经网络的选择。下表说明,在 FL 中,采用聚合底层神经网络而保持核函数参数局部更新的部分聚合方法实现了局部个性化和全局泛化的平衡;使用 RBF 核与 ResNet 神经网络的深度核函数取得了最佳的分类和回归效果。

结论
总的来说,本文强调联邦学习中同质性任务的局限性,提出融合局部水平下的多任务学习和全局水平下的联邦学习的多任务联邦学习算法。作者使用 MOGP 刻画任务间的相关性,并引入 Polya-Gamma 数据增强技术,推导出闭式的 mean-field 变分推断框架。
实验结果展示了模型在预测效果、不确定性校准、样本外检测和收敛速度上的优越表现,强调了模型在多种应用场景下的潜力。值得指出的是,本文采用的实验设定仅为了计算和展示上的便利,实际情况中 pFed-Mul 可以推广至多种任务(超过本文使用的两种任务),以及局部设备之间的任务多样性。
(文:PaperWeekly)














