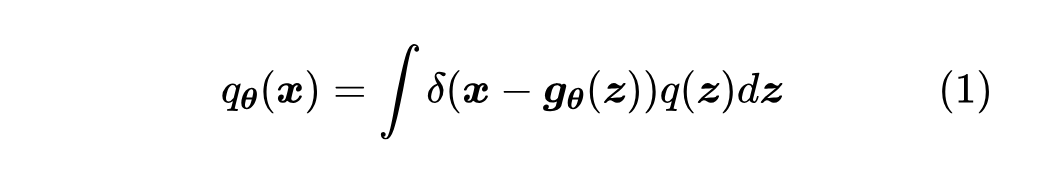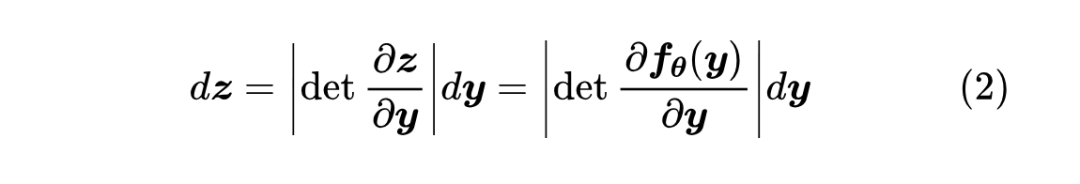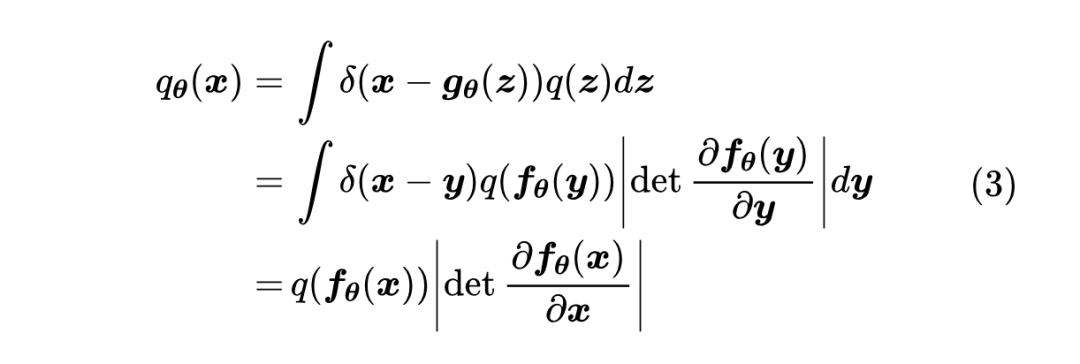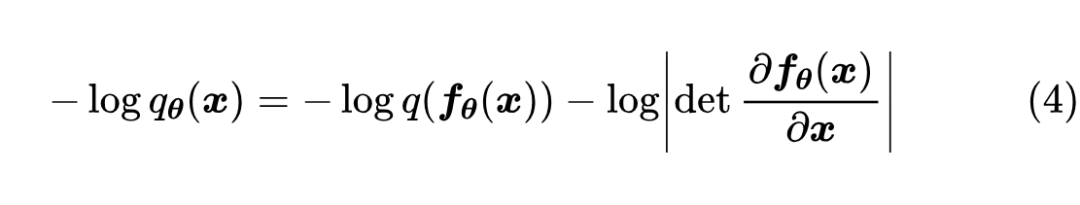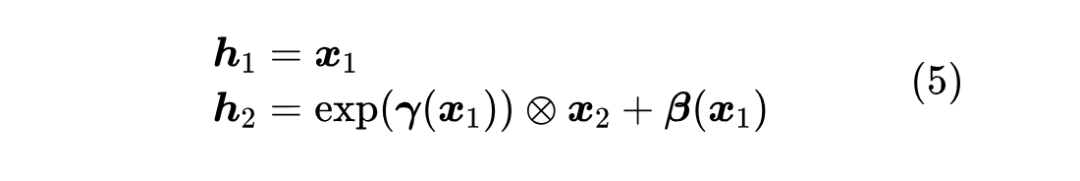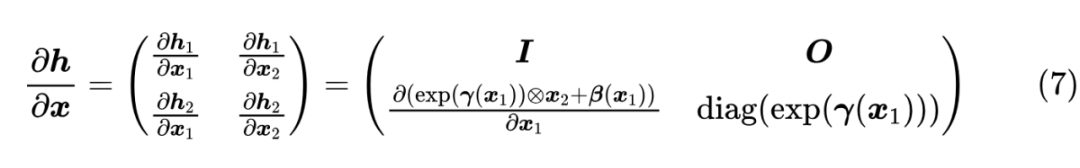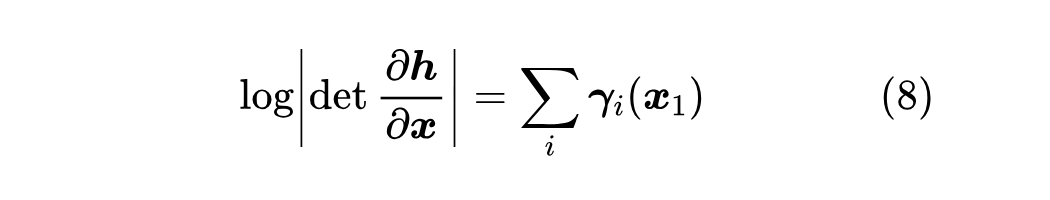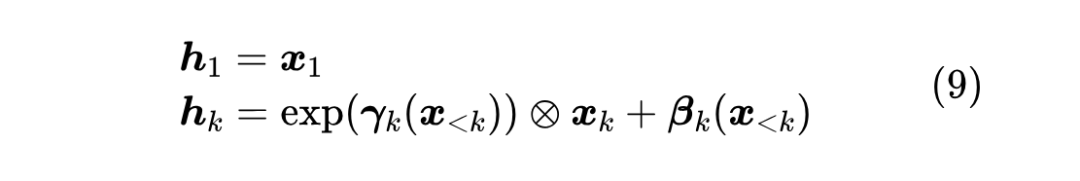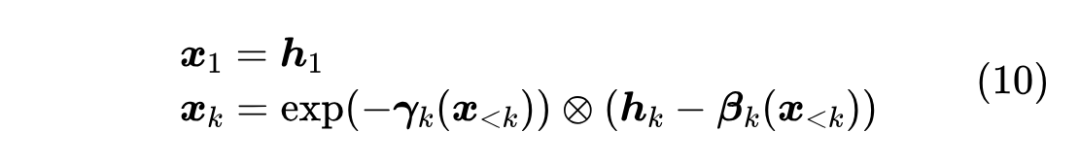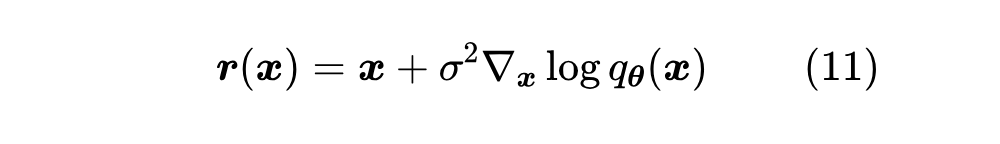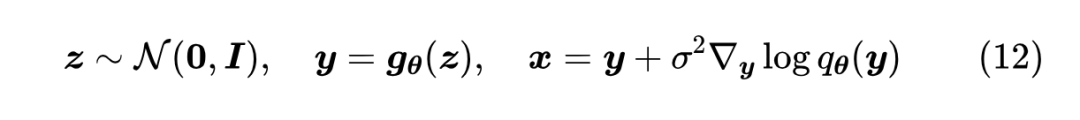细水长flow之TARFLOW：流模型满血归来？

©PaperWeekly 原创 · 作者 | 苏剑林

单位 | 科学空间

研究方向 | NLP、神经网络

不知道还有没有读者对这个系列有印象？这个系列取名“细水长 flow”，主要介绍 flow 模型的相关工作，起因是当年（2018 年）OpenAI 发布了一个新的流模型 Glow，在以 GAN 为主流的当时来说着实让人惊艳了一番。

但惊艳归惊艳，事实上在相当长的时间内，Glow 及后期的一些改进在生成效果方面都是比不上 GAN 的，更不用说现在主流的扩散模型了。

不过局面可能要改变了，前段时间的论文《Normalizing Flows are Capable Generative Models》[1] 提出了新的流模型 TARFLOW，它在几乎在所有的生成任务效果上都逼近了当前 SOTA，可谓是流模型的“满血”回归。

写在前面

这里的流模型，特指 Normalizing Flow，是指模型架构具有可逆特点、以最大似然为训练目标、能实现一步生成的相关工作，当前扩散模型的分支 Flow Matching 不归入此列。

自从 Glow 闪耀登场之后，流模型的后续进展可谓“乏善可陈”，简单来说就是让它生成没有明显瑕疵的 CelebA 人脸都难，更不用说更复杂的 ImageNet 了，所以“细水长 flow” 系列也止步于 2019 年的《细水长 flow 之可逆 ResNet：极致的暴力美学》。

不过，TARFLOW 的出现，证明了流模型“尚能一战”，这一次它的生成画风是这样的：

▲ TARFLOW 的生成效果

相比之下，此前 Glow 的生成画风是这样的：

▲ Glow 的生成效果

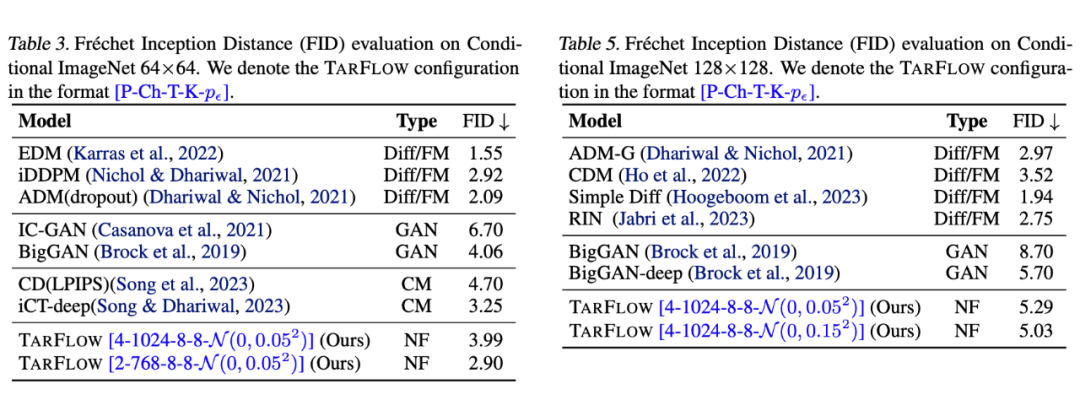
Glow 演示的还只是相对简单的人脸生成，但瑕疵已经很明显了，更不用说更复杂的自然图像生成了，由此可见 TARFLOW 的进步并不只是一星半点。从数据上看，它的表现也逼近模型模型的最佳表现，超过了 GAN 的 SOTA 代表 BigGAN：

▲ TARFLOW 与其他模型的定量对比

要知道，流模型天然就是一步生成模型，并且不像 GAN 那样对抗训练，它也是单个损失函数训练到底，某种程度上它的训练比扩散模型还简单。所以，TARFLOW 把流模型的效果提升了上来，意味着它同时具备了 GAN 和扩散模型的优点，同时还有自己独特的优势（可逆、可以用来估计对数似然等）。

模型回顾

言归正传，我们来看看 TARFLOW 用了什么“灵丹妙药”来让流模型重新焕发活力。不过在此之前，我们简要回顾一下流模型的理论基础，更详细的历史溯源，可以参考《细水长 flow之NICE：流模型的基本概念与实现》和《细水长 flow 之 RealNVP 与 Glow：流模型的传承与升华》。

从最终目标来看，流模型和 GAN 都是希望得到一个确定性函数 ，将随机噪声 映射到目标分布的图片 ，用概率分布的语言说，就是用如下形式的分布来建模目标分布：

其中 是狄拉克 δ 函数 [2]。训练概率模型的理想目标是最大似然，即以 为损失函数。但目前的 带有积分，只有形式意义，无法用于训练。

此时流模型和 GAN 就“分道扬镳”了：GAN 大致上是用另外一个模型（判别器）去近似 ，这导致了交替训练；流模型则通过设计适当的 ，让积分（1）可以直接算出来。把积分（1）算出来需要什么条件呢？设 ，其逆函数为 ，那么

以及

因此

这表明，将积分（1）算出来需要两个条件：一、需要知道 的逆函数 ；二、需要计算雅可比矩阵 的行列式。

仿射耦合

为此，流模型提出了一个关键设计——“仿射耦合层”：

其中 ，、 是以 为输入、输出形状跟 一致的模型， 是 Hadamard 积。上式说的是，将 分成两部份，分法随意，也不要求等分，将其中一份原封不动输出，另一边按照指定规则运算输出。注意仿射耦合层是可逆的，其逆为

这就满足了第一个条件可逆性。另一方面，仿射耦合层的雅可比矩阵是一个下三角阵：

三角矩阵的行列式，等于对角线元素之积，所以

即雅可比矩阵行列式的绝对值对数等于 的各分量之和，这就满足了第二个条件雅可比矩阵行列式的可计算性。

仿射耦合层首次提出自 RealNVP [3]，NVP 的含义是 “Non-Volume Preserving”，也就是“不保体积”，这个名字对标的是 恒等于零时的特殊情形，此时称为“加性耦合层”，提出自 NICE [4]，特点是其雅可比行列式等于 1，即加性耦合层是“保体积”的（行列式的几何意义是体积）。

注意，如果直接堆叠多个仿射耦合层，那么 将一直保持不变，这并不是我们想要的，我们想要做的是将整个 映射到标准正态分布。为了解决这个问题，我们每次应用仿射耦合层前，都要输入的分量以某种方式“打乱”，这样就不至于出现始终不变的分量。“打乱”运算对应于置换矩阵变换，行列式绝对值始终为 1。

核心改进

到目前为止，这些内容都还只是流模型的基础内容，接下来才正式进入到 TARFLOW 的贡献点。

首先，TARFLOW 留意到仿射耦合层（5）可以推广到多块划分，即将 分成更多份 ，然后按照类似的规则运算

其中 ，，其逆运算为

类似地，推广版本的仿射耦合层的雅可比行列式绝对值对数为 的所有分量之和，所以流模型要求的两个条件都能满足。这个推广的雏形最早在 2016 年的 IAF 就提出了，比 Glow 还早。

可为什么后来的工作鲜往这个方向深入呢？这大体是历史原因。早年 CV 模型的主要架构是 CNN，用 CNN 的前提是特征满足局部相关性，这就导致了将 分块时，往往只考虑在通道（channel）维度划分。

因为每一层还有一个必要的打乱运算，一旦选择在长、宽两个空间维度划分，那么随机打乱后特征就失去了局部相关性了，从而没法用 CNN。而如果在通道维度划分多份，那么多个通道特征图比较难高效地交互。

然而，到了 Transformer 时代，情况截然不同了。Transformer 的输入本质上是一个无序的向量集合，换言之不依赖局部相关性，因此以 Transformer 为主架构，我们就可以选择在空间维度划分，这就是 Patchify。

此外，式（9）中 形式，意味着这是一个 Causal 模型，这也正好可以用 Transformer 高效实现。

除了形式上的契合外，在空间维度划分有什么本质好处呢？

这就要回到流模型的目标了： 将噪声变成图片，逆模型 则将图片变成噪声，噪声的特点是随机，说白了就是乱，图片的显著特点是局部相关性，所以图片变噪声的关键之一就是要打乱这种局部相关性，直接在空间维度 Patchify 配合耦合层自带的打乱操作，无疑是最高效的选择。

所以，式（9）跟 Transformer 可谓是“一拍即合”、“相得益彰”，这就是 TARFLOW 前三个字母 TAR 的含义（Transformer AutoRegressive Flow），也是它的核心改进。

加噪去噪

流模型常用的一个训练技巧是加噪，也就是往图片加入微量噪声后再送入模型进行训练。虽然我们将图片视为连续向量，但它实际是以离散的格式存储的，加噪可以进一步平滑这种不连续性，使得图片更接近连续向量。噪声的加入还可以防止模型过度依赖训练数据中的特定细节，从而减少过拟合的风险。

加噪是流模型的基本操作，并不是 TARFLOW 首先提出的，TARFLOW 提出的是去噪。理论上来说，图片加噪后训练出来的流模型，生成结果也是带有噪声的，只不过以往的流模型生成效果也没多好，所以这点噪声也无所谓了。但 TARFLOW 把流模型的能力提上去后，去噪就“势在必行”了，不然噪声就称为影响效果的主要因素了。

怎么去噪呢？另外训练一个去噪模型？没这个必要。我们在《从去噪自编码器到生成模型》已经证明了，如果 是加噪 训练后的概率密度函数，那么

就是去噪模型的理论最优解。所以有了 后，我们就不用另外训练去噪模型了，直接按照上式计算就可以去噪，这也是流模型的优势之一。而正因为加入了去噪步骤，所以 TARFLOW 的输入的噪声改为高斯分布，并适当增大了噪声的方差，这也是它性能更好的原因之一。

综上所述，TARFLOW 完整的采样流程是

延伸思考

至此，TARFLOW 相比以往流模型的一些关键变化已经介绍完毕，剩下的一些模型细节，大家自行读原论文就好，如果还有不懂的也可以参考官方开源的代码。

Github:

https://github.com/apple/ml-tarflow

下面主要谈谈笔者对 TARFLOW 的一些思考。

首先，需要指出的是，TARFLOW 虽然效果上达到了 SOTA，但它采样速度实际上不如我们期望，原论文附录提到，在 A100 上采样 32 张 ImageNet64 图片大概需要 2 分钟。

为什么会这么慢呢？我们仔细观察耦合层的逆（10）就会发现，它实际上是一个非线性 RNN！非线性 RNN 只能串行计算，这就是它慢的根本原因。

换句话说，TARFLOW 实际上是一个训练快、采样慢的模型，当然如果我们愿意也可以改为训练慢、采样快，总之正向和逆向不可避免会有一侧慢，这是分多块的仿射耦合层的缺点，也是 TARFLOW 想要进一步推广的主要改进方向。

其次，TARFLOW 中的 AR 一词，容易让人联想到现在主流的自回归式 LLM，那么它们俩是否可以整合在一起做多模态生成？

说实话很难。因为 TARFLOW 的 AR 纯粹是仿射耦合层的要求，而耦合层之前还要打乱，所以它并非一个真正的 Causal 模型，反而是彻头彻尾的 Bi-Directional 模型，所以它并不好跟文本的 AR 强行整合在一起。

总的来说，如果 TARFLOW 进一步将采样速度也提上去，那么它将会是一个非常有竞争力的纯视觉生成模型。

因为除了训练简单和效果优异，流模型的可逆性还有另外一个优点，就是《The Reversible Residual Network: Backpropagation Without Storing Activations》[5] 所提的反向传播可以完全不用存激活值，并且重计算的成本比普通模型低得多。

至于它有没有可能成为多模态 LLM 的统一架构，只能说现在还不大明朗。

文艺复兴

最后，谈谈深度学习模型的“文艺复兴”。

近年来，已经有不少工作尝试结合当前最新的认知，来反思和改进一些看起来已经落后的模型，并得到了一些新的结果。除了 TARFLOW 试图让流模型重新焕发活力外，最近还有《The GAN is dead; long live the GAN! A Modern GAN Baseline》[6] 对 GAN 的各种排列组合去芜存菁，得到了同样有竞争力的结果。

更早一些，还有《Improved Residual Networks for Image and Video Recognition》[7]、《Revisiting ResNets: Improved Training and Scaling Strategies》[8] 等工作让 ResNet 更上一层楼，甚至还有《RepVGG: Making VGG-style ConvNets Great Again》[9] 让 VGG 经典再现。

当然，SSM、线性 Attention 等工作也不能不提，它们代表着 RNN 的“文艺复兴”。

期待这种百花齐放的“复兴”潮能更热烈一些，它能让我们获得对模型更全面和准确的认知。

（文：PaperWeekly）