神经网络是怎么学习的？

今天这篇文章主要是用来记录一个问题，神经网络是怎么学习的？

这个问题是在昨天写神经网络的开发框架——PyTorch和神经网络架构——Transformer架构时突然发现的一个问题。

在学习大模型或者说神经网络的过程中，我们知道一件事就是，神经网络在设计完成之后，需要经过大量的数据进行训练；具体流程就是要把训练数据输入到模型中，然后模型经过一系列的处理，如损失计算，参数调整(反向传播算法)，一步一步的把模型参数调整到最优解。

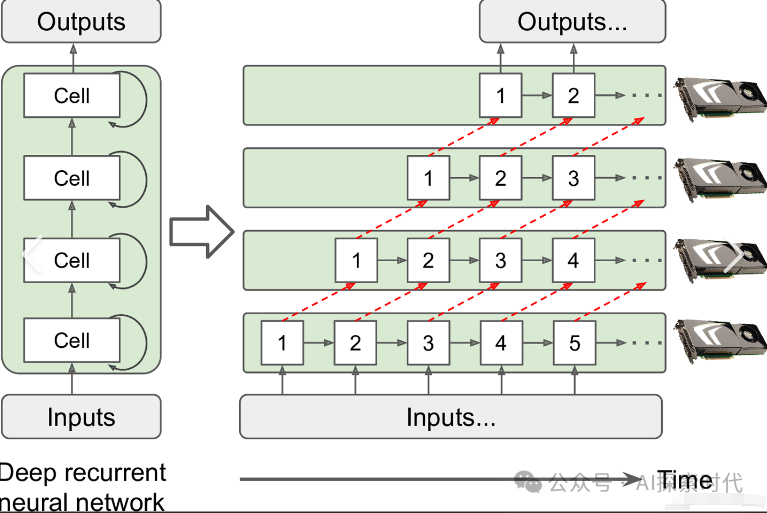
但是从PyTorch框架来看，所谓的模型训练就是在不断的进行数学运算，包括矩阵运算，求导等等；而从Transformer架构来看，模型训练就是经过架构中的编码器和解码器，通过数学计算的方式提取数据的特征，最终获得结果。

这里就产生了一个问题，那就是为什么数据经过一系列数学运算之后，就可以学习到数据的特征；虽然说模型是通过矩阵运算，把数据转化为向量之后，通过计算向量之间的数学关系来表示数据的特征；比如说，欧式距离，平方差等。

在多维的向量空间中，具有语义或关联性的数据在多维空间中就会呈现一定的数学关系；但神经网络是怎么知道它们之间的数据关系的？

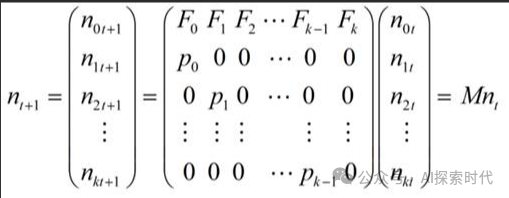
在无监督学习中，数据之间的关系是模型根据自身的数学规则去计算训练数据的潜在关系；而在监督学习中，模型是通过损失函数计算训练数据与目标结果的数学关系——损失差；之后在经过调优函数进行反向传播，动态调整模型参数的过程。

所以，从表现来看神经网络之所以能学习到数据特征，主要原因并不在于数学计算，而在于怎么进行这个数学计算，比如第一步该怎么算，第二步该怎么算；最终计算出一个结果。

因此，神经网络模型就类似于一个数学领域中的函数，也就是y=f(x)，核心就在于这个f——数学关系。

而神经网络这个函数f(x)和普通函数的区别就在于，普通函数是一个具备一定关系的数学公式，其参数和关系是固定的；而神经网络这个函数的参数和关系却是可以动态调整的。

怪不得很多人说，神经网络的本质就是一个数学问题，更严格的说法应该是数学领域中的向量问题；而具体表现为矩阵运算。

训练数据被转换为向量之后，神经网络模型就对这个向量进行七颠八倒的变换。

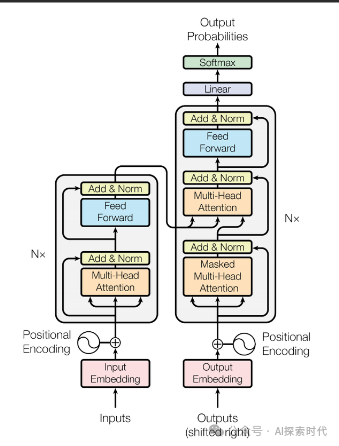
总的来说，神经网络的载体是向量，方法是矩阵运算，核心是数学关系——也就是进行怎样的数学计算，其数学原理是什么？也就是说y=f(x)的这个f到底是什么？

看来是时候需要研究一下Transformer的论文——《Attention is All You Need》了。