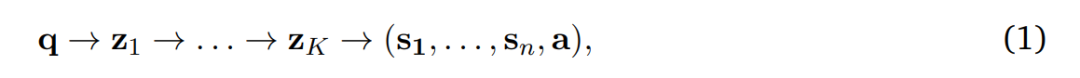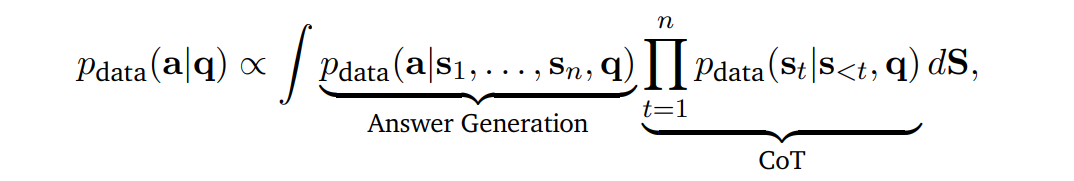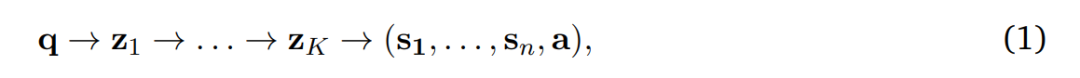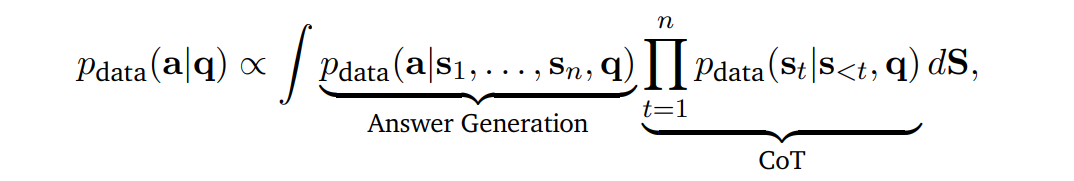跳至内容
Meta-CoT 通过显式建模生成特定思维链(CoT)所需的底层推理过程,扩展了传统的思维链方法。
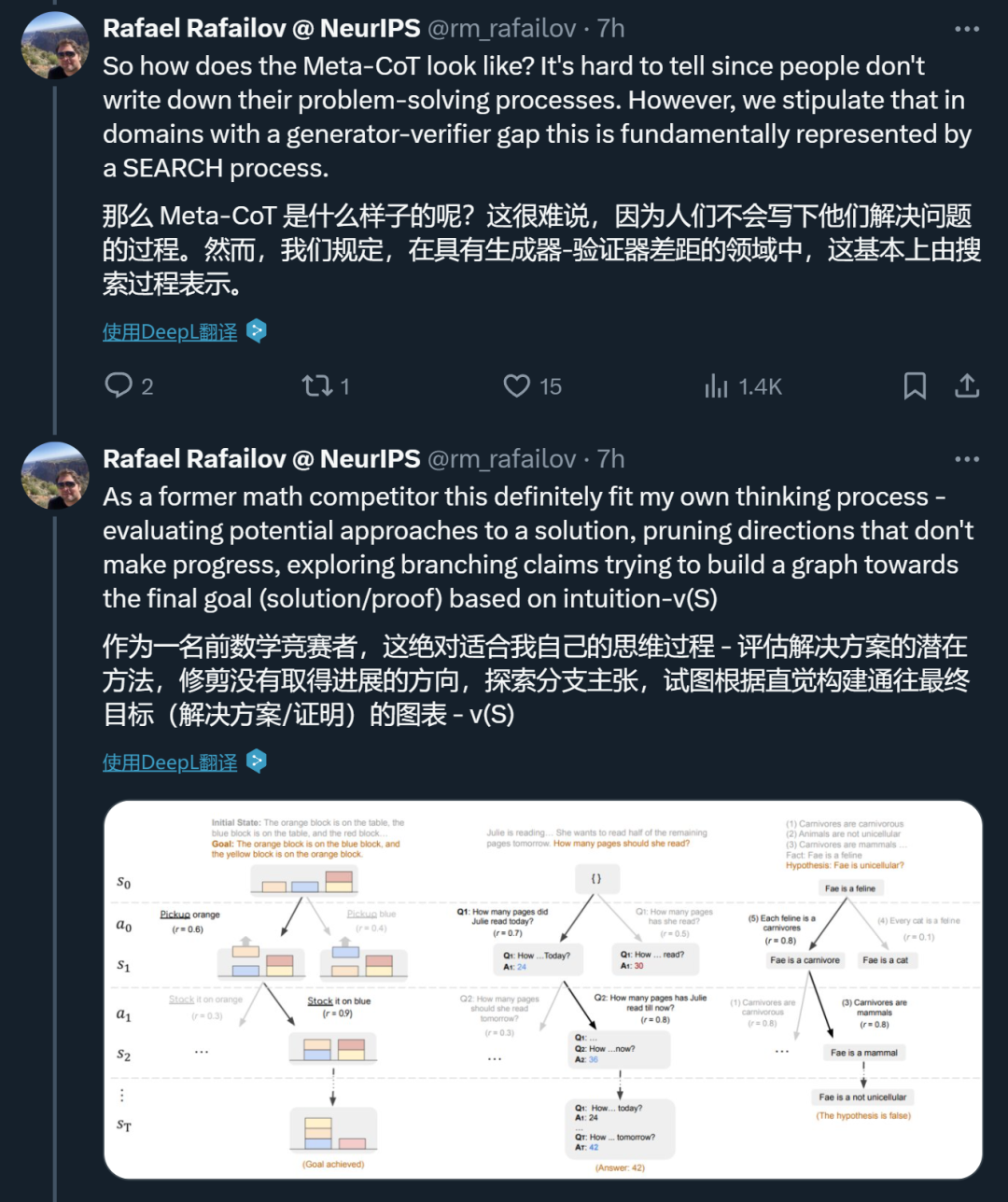
「我们有一份关于『推理时间计算』的新研究,以及我们过去几个月一直在研究的内容!我们提出了一些理论,说明为什么它是必要的,它是如何工作的,我们为什么需要它,以及它对超级智能意味着什么。」
刚刚,斯坦福博士生 Rafael Rafailov 在 X 上官宣了一项他参与的新研究《 Towards System 2 Reasoning in LLMs: Learning How to Think With Meta Chain-of-Thought 》。
Rafailov 进一步表示,「我们需要高级推理的主要原因在于问题的复杂性。模型训练数据中虽然包含了难题的解决方案,但并未涵盖这些解决方案的真实数据生成过程。解决方案本身是某种复杂的元思维链(Meta-CoT)的输出,而这一过程并未被明确记录下来。」
图为解决一个数学问题的过程,这个问题是要找到一种运算符序列(包括加号 +、减号 -、乘号 * 和除号 /),使得数字 7、3、11、5 通过这些运算恰好使用一次得到结果 24。
Rafailov 所说的 Meta-CoT,是一种新颖的框架,它通过显式建模生成特定思维链(CoT)所需的底层推理过程,扩展了传统的思维链方法。
该研究认为,传统的 CoT 方法虽然在解决简单问题时有效,但未能捕捉到复杂推理的真实数据生成过程,这一过程通常涉及非线性、迭代性和潜在的探索与验证。Meta-CoT 通过显式建模这种潜在的「思考」过程,扩展了 CoT 方法。本文认为,这种建模对于解决需要高级推理能力的问题至关重要。
-
论文地址:https://arxiv.org/pdf/2501.04682
该研究从认知科学的双过程理论中汲取灵感,将 Meta-CoT 框架看作为一种 System 2 推理形式。本文奠定了 Meta-CoT 理论基础,展示了如何通过系统搜索过程实现这一框架,以及如何将这些过程内化到一个单一的自回归模型中。随后,本文提供了实证证据,包括对 OpenAI 的 o1 和 DeepSeek-R1 等顶尖模型的分析,这些模型展现出了与内化(上下文)搜索一致的行为。接着本文进一步探索了通过过程监督来训练 Meta-CoT 模型的方法,以及通过蒙特卡洛树搜索(MCTS)和 A * 等搜索算法生成合成数据的技术。
最后,本文概述了一个在单一端到端系统中实现 Meta-CoT 的具体流程,该流程结合了带有线性化搜索痕迹的指令调整和强化学习(RL)后训练。
本文还介绍了一个名为 Big MATH 的项目,该项目整合了超过 100 万个高质量、可验证的数学问题,以促进这一领域进一步研究。
该研究不仅提供了理论洞见,还为在 LLM 中启用 Meta-CoT 提供了一条实践路线图,为人工智能实现更强大和更类人的推理铺平了道路。
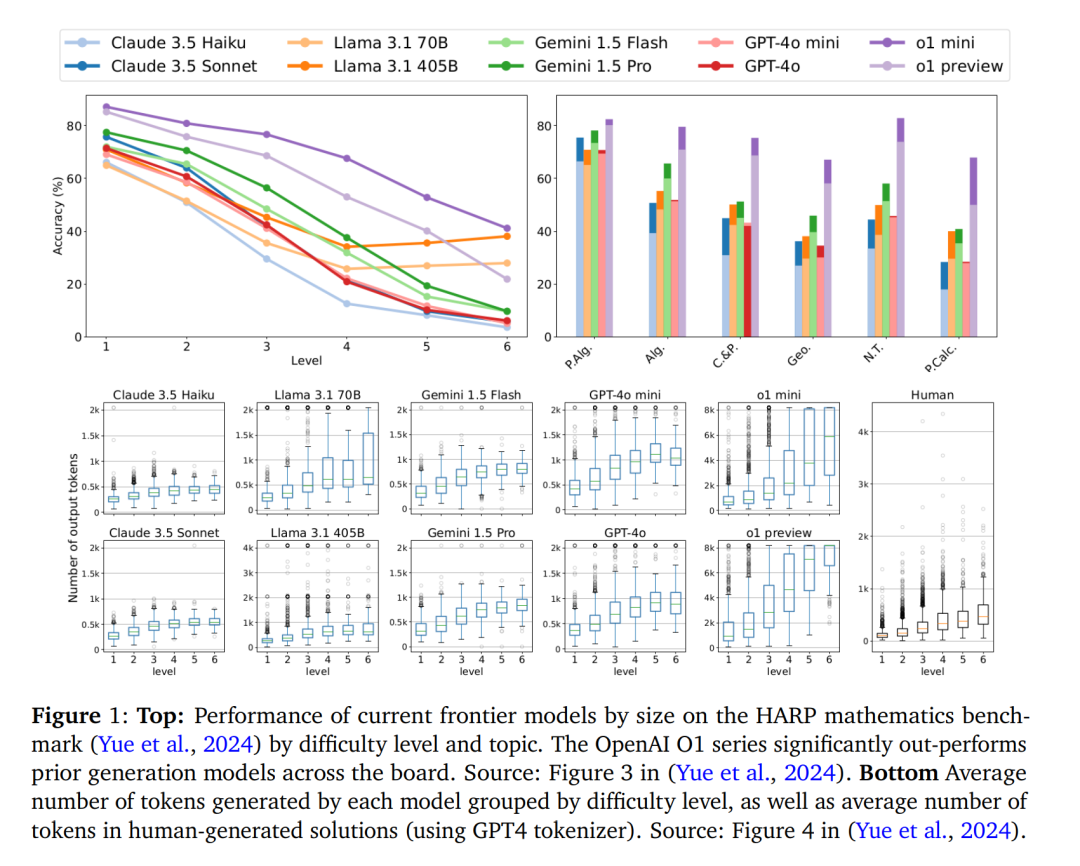
我们要问自己一个问题:具有「思维链」提示功能的语言模型是否真的能够表达任何函数,从而解决任意复杂的问题?今天,前沿模型的能力足以解决一大类数学推理问题。但是,它们仍然难以解决高级问题,如 HARP 和 Omni-MATH(通用奥林匹克级别数学基准)。作者提出了以下理论来解释这些经验观察结果:
预训练语料库中的推理数据并不代表真正的数据生成过程,尤其是复杂问题的数据生成过程,它是大量潜在推理的产物。此外,这一过程一般不会以从左到右、自回归的方式进行。
更详细地说,预训练语料库和后训练指令微调中普遍存在的思维链(CoT)推理数据遵循简单问题(如代数计算、计数、基础几何等)解决方案的真实数据生成过程。例如,解决高中代数问题的教科书展示了生成答案的一般过程。如果我们遵循现有教科书中呈现的一些步骤或方法,我们最终可以得出解答。因此,这些可以通过具有恒定深度的 transformer 来学习,这些 transformer 能够表达过程中每个单独步骤的复杂性。
相比之下,复杂推理问题并不遵循这种模式。我们可能有一组三元组(q, S, a),其中 q 是问题,S = (s_1, …, s_n) 是解答步骤,a 是(可选的)答案,但真实的数据生成过程并非自回归的:
z_𝑖是解答步骤中遗漏的潜在「思考」,这些可以通过从左到右的生成来完全表示,而数据集中的解答步骤 S = (s_1, …, s_n) 是联合生成的。
我们可以通过将推理解释为潜在变量过程来形式化这一论证。具体来说,经典的思维链(CoT)可以被看作是:
即,最终答案产生的概率是通过对潜在推理链的边缘化得到的。作者主张,对于复杂问题,真实的解生成过程应该被视为:
即,解(a,s_1, . . . , s_n)的联合概率分布以潜在生成过程为条件。请注意,这个参数是先前的 CoT 参数的 meta-generalization,因此作者将过程 q→z_1 → . . . → z_K 称为 Meta-CoT。
根据之前的讨论,一个问题自然地浮出水面:为什么 LLM 在这些高级推理任务上失败了?如上所述,作者提出了预训练和指令微调语料库由类型为(q, s_1, …, s_n, a)的数据组成,这些数据并不包含如方程 1 所示的真实数据生成过程。这个现象很常见 —— 教科书包含高级证明,但不包含推导这些证明的完整思考过程。
很多使用传统思维链的工作受此影响,但 OpenAI 的 o1 系列看起来是个例外。作者表示,他们在困难的数学问题上看到了这种差异:「标准」模型会「模仿」人类编写的解决方案(训练数据),而像 o1 这样的模型则根据难度逐步使用更多的计算。它似乎遵循真正的数据生成过程,而不仅仅是最终输出(CoT)。
上一节介绍了 Meta-CoT 过程,并指出 LLM 在高级推理任务上表现不佳的原因是训练数据未能充分代表真实的数据生成过程,即文本语料库中未包含(或仅包含有限数量的)Meta-CoT 数据。因此,剩下的问题是:真实的数据生成过程是什么样的?
首先,本文主张对于许多高级推理或目标导向问题,生成(问题的解决过程)和验证(解决方案的正确性检验)之间存在显著的复杂性 gap。
其次,假设存在一个不可忽视的生成器 – 验证器 gap,作者认为文本语料库中呈现的挑战性问题的解决方案是一个扩展搜索过程的结果,这个过程本身在数据中并没有得到体现。
作者表示,事实上,在基本策略之上构建搜索能力已经一次又一次地被证明会带来巨大的能力提升。不过,这需要更多数量级的 scale 和数据才能内化到单个模型中。
为什么需要将深思熟虑的推理过程内化到一个单一模型中?作者提出了两个主要原因:
首先是效率:通过在自回归模型的上下文中整合搜索,可以有效地完成探索,因为模型可以访问上下文中所有先前访问过的节点。事实上,正如图 14 所示,即使是高级推理模型也会执行许多语义相同的重复推理步骤。
其次是超级智能:如果一个自回归模型能够学会在上下文中实现搜索算法,那么额外的强化学习(RL)训练可能使模型发现新的推理方法。这将可能使模型能够解决在基于符号的树搜索方法下解决以前无法解决的问题类别。
在接下来的部分,作者进一步探讨了如何训练一个模型来内化这样一个推理系统。
作者介绍了 STaR(Self-Taught Reasoner)方法背后的核心思想,该方法用于引导中间 CoT 步骤,以及如何将类似的概念泛化到元推理策略中。
具体而言,STaR 方法引入了一种迭代 bootstrapping 方法,旨在提高 LLM 的推理能力。STaR 专注于训练模型以生成和完善推理过程,特别是对于需要复杂推理的任务,其采用了基于强化学习的方式来进行。
之后作者将 STaR 的思路扩展到 Meta-CoT。
本文探索了两种用于生成合成训练数据的主要搜索算法:蒙特卡洛树搜索 (MCTS) 和 A* 变体。
与图 12 中由蒙特卡洛树搜索(MCTS)产生的路径相比,A* 搜索具有更少的回溯步骤,主要集中在关键步骤上。
搜索方法的一个关键组成部分是评估函数𝑣(q, S_𝑡),它对推理链中的中间状态进行评分。这些评估函数被广泛称为过程奖励模型(Process Reward Models,简称 PRM)。通过整合过程监督,搜索机制获得了在遇到次优路径时回溯到早期有前景状态的灵活性,从而实现了更有效的探索。然而,如何有效地获取这些能力仍然是一个未解决的问题。
在论文第 6 章,作者从元学习和元强化学习的角度对推理问题和 Meta-CoT 进行解释。
在前面章节中,作者通过计算复杂性和生成器 – 验证器 gap 的范例来激发上下文搜索的需求。在本节中,作者建立了一个替代公式,以帮助形式化强化学习训练的实证结果。
作者假设奖励函数𝑟(S, q) → {0, 1} 是提示 q 的确定性(但先验未知)函数,它只接受特定的解决方案集。在新的提示下进行测试时,这会产生奖励函数的认知不确定性,即我们事先不知道该任务(提示问题)的完整接受或拒绝的解决方案集。
在接下来的第 7 章,作者提出了一种基于搜索的高级推理理论,以及一些早期的实证研究结果。作者建议遵循现代后训练的整体结构,包括指令微调和强化学习训练。感兴趣的读者,可以查看原论文了解更多内容。
本文引入了 Meta-CoT 框架,用于理解和增强大型语言模型(LLMs)的推理能力。作者认为传统的思维链并不能完全代表推理问题背后的数据生成过程。通过融入搜索、验证和迭代优化的概念,Meta-CoT 为高级问题解决所需的认知过程提供了一个更完整的模型。
Meta-CoT 是实现大型语言模型更强大、更具泛化性推理能力的一种有前景的途径。当前最先进模型的表现,以及在上下文探索和回溯方面的实验,都支持了内部搜索过程对于复杂任务表现至关重要的假设。此外,本文提出的训练流程为开发具有增强 Meta-CoT 能力的大型语言模型提供了一种具体的方法。
(文:机器之心)