
如果你对大语言模型(LLM)的强化学习(RLHF)感兴趣,又想从最基础的策略梯度优化一路了解、推导出 PPO、GAE,再深入探讨 DPO,那你就来对地方了。
本文将从最基础的 Gradient Policy Optimization 开始,逐步介绍经典的 REINFORCE 算法,再讲解如何利用剪切目标实现近端策略优化(PPO),并通过广义优势估计(GAE)在偏差与方差之间找到最佳平衡。之后,我们还会从头推导、讨论离线训练方法,如 DPO,帮助你了解不同训练路线的优势与挑战。

在线(On-Policy)和离线(Off-Policy)强化学习
-
以 PPO 为代表的 On-Policy 路线
-
以 DPO 为代表的 Off-Policy 路线
-
On-Policy:训练过程中,需要模型亲自参与“生成”来收集新的数据样本。
-
Off-Policy:训练过程中,不需要“在线”生成,更多依赖事先收集到的(或由别的策略产生的)数据进行离线学习。
一般来说,On-Policy 的方法在训练时会更“耗卡”、更耗时——最大的开销主要是源自“模型生成”这一步,因为对一个生成式任务而言,模型需要逐 token 地输出,这个过程极其耗费算力。
不过,尽管速度较慢,On-Policy 在理论上拥有更高的效果上限,因为它能够不断根据当前模型状态进行探索和更新,这一点将在后续讨论 PPO 时更加凸显。
我们首先来谈谈 On-Policy 路线。On-Policy 的核心思路是:让模型自己产出答案,然后依据答案的优劣来打分,以此指导下一步的参数更新。简而言之,最关键的一点是让模型“亲自下场”。
-
方式一:让你真刀真枪地下棋,每一步都有教练跟在你身边打分。当你吃掉对手棋子时,教练会鼓励你;当你因为冲动失误被对面反杀时,教练会及时提醒你改进。
-
方式二:给你一堆职业选手的比赛录像和一堆臭棋篓子的对局,用标注告诉你哪些操作是好招,哪些操作是坏招,然后你被动地学这些好操作、避免坏操作。
这两种方式最大的区别就在于:你有没有亲自去“下棋”。方式一就是 On-Policy,需要模型自己产出行为,然后学习;方式二就是 Off-Policy,只需根据已有对局数据进行模仿式学习。
Off-Policy 在训练时通常更快,因为它用现成的数据就可以了,不需要模型时时在线生成并等待打分,但也很依赖这批数据与当前模型能力的“匹配度”。如果数据中操作难度和模型水平相差太大(过高或过低),学习效果就可能大打折扣;On-Policy 则可以避免这一问题,因为它所得到的训练样本 100% 来自于自己当前的水平和行动。
-
Actor:负责“生成”句子的模型(就像正在对弈的你)。 -
Critic:类似于“教练”,为每个生成结果提供即时指导;它本身也在训练过程中随 Actor 的能力变化而调整。 -
Reward Model:相当于“裁判”,给出最终分数或偏好评估。通常在训练过程中是固定不动的。 -
Reference Model:PPO 在大模型里的“独有角色”,用来防止 Actor 过度偏离原有预训练分布,缓解 reward hacking 等问题。
由于在大型 LLM 上,这四个部分的参数量都可能非常庞大(往往需要同时加载多个 70B 参数规模的模型),所以 On-Policy 训练往往带来极高的算力需求,这也是为什么人们通常说 PPO“非常耗卡”的原因。
下一步,我们将把目光聚焦在当前 On-Policy 路线最具代表性的方法——PPO 上,看看它究竟如何在实践中平衡训练开销与学习效率。

PPO(近端策略优化)
2.1 从策略梯度优化(Policy Gradient Optimization)谈起
想象一下,你是一名刚开始学习下象棋的新手。你的目标是通过不断调整你的下棋策略(记作 ,其中 表示你的策略参数),来提高在一局棋中获得胜利的概率,也就是最大化你的期望回报。我们可以将每一盘棋看作是一条轨迹 ,而你要做的,就是通过不断优化你的策略来获得更高的回报。

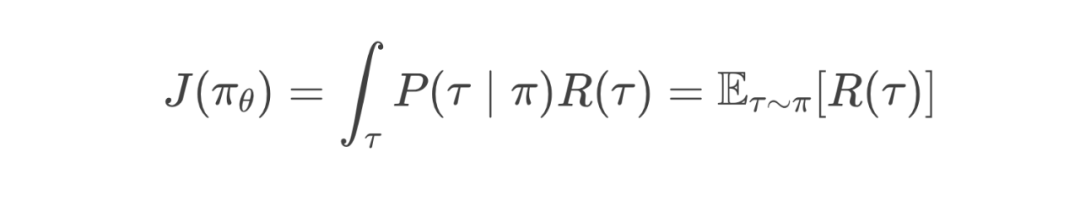

在下棋这个例子中,状态 可以理解为当前棋盘落子的状态,而动作 即为下一次落子的地方。而当前时间点的下一个状态,则服从某种概率分布,可以被看作是随机的、不确定的(即对手落子):
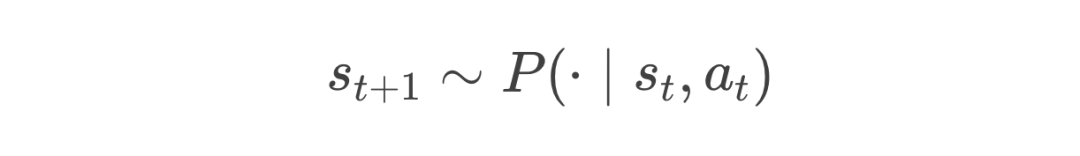
那么一个轨迹 的概率则为:
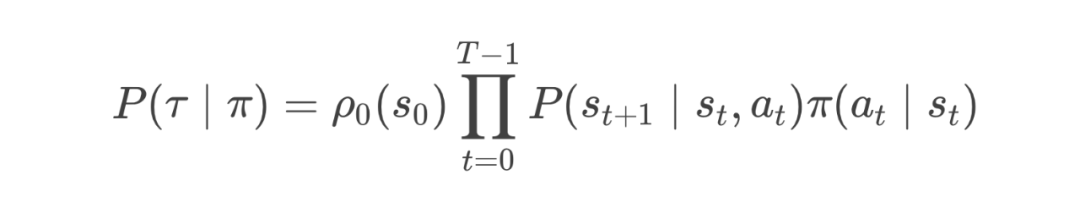
在强化学习中,我们会不断提到回报会随着时间不断打折 (discount reward) 的概念:未来的回报总是不如当下的回报那么重要。所以一个策略 的总回报可以被视作:
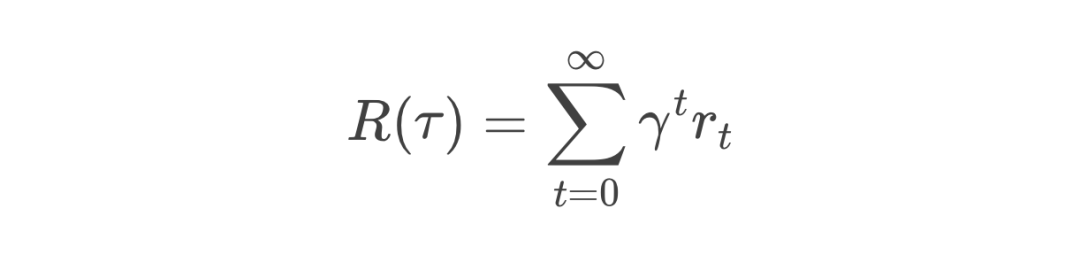
其中 是时间上的折扣因子,而 是 时刻的实际回报。

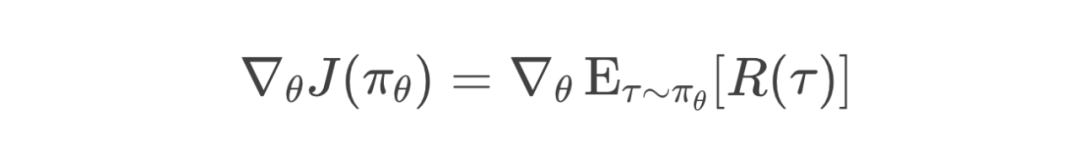
第1步:展开期望(Expand the Expectation)
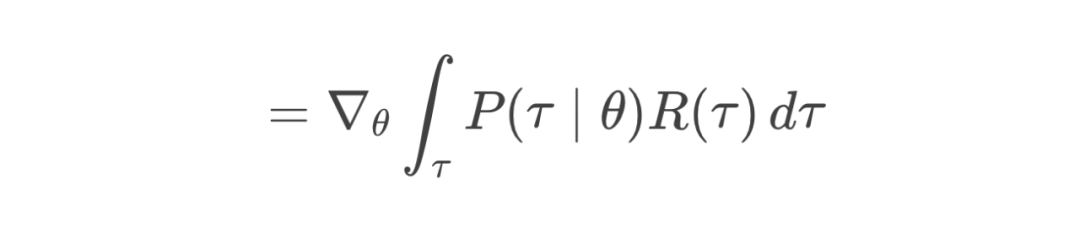
第2步:交换梯度与积分(Interchange Gradient and Integral)

第3步:使用对数导数技巧(Apply Log-Derivative Trick)

第4步:回到期望形式(Return to Expectation Form)
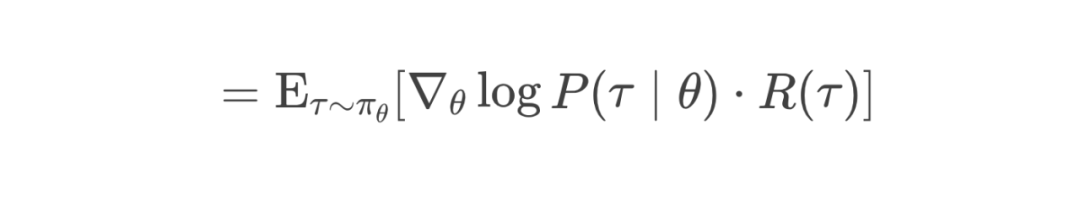

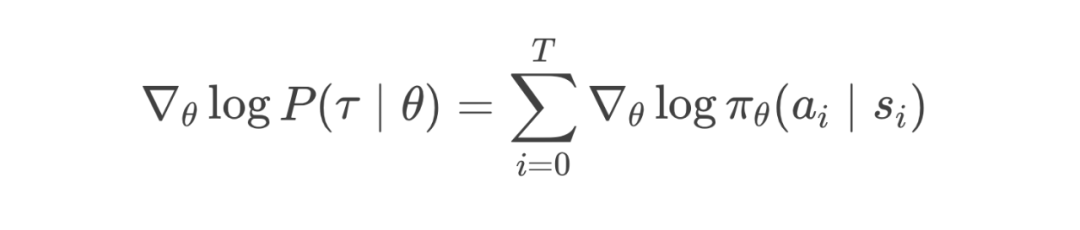
2.2 最终策略梯度公式(Final Policy Gradient Formula)
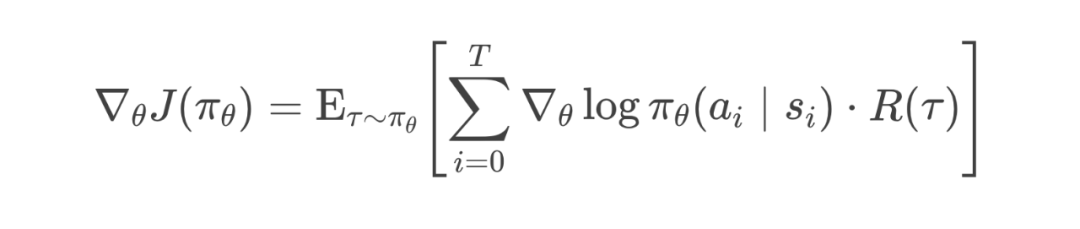
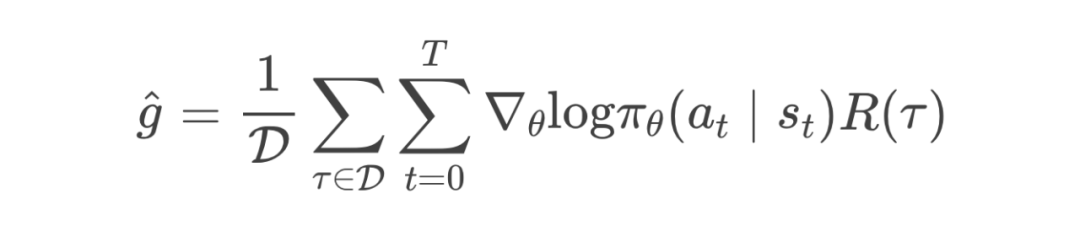
2.3 REINFORCE 算法流程与实现步骤
-
输入:当前棋局状态 -
输出:根据当前棋局生成下一步棋的概率分布
2. 轨迹采样
-
你可以设定每盘棋固定步数(比如 100 步),或直到比赛结束。
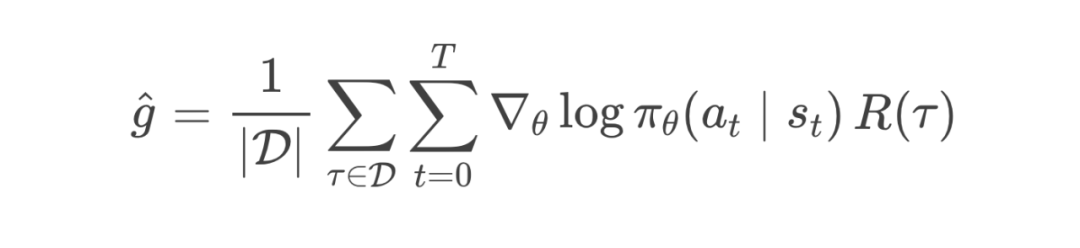
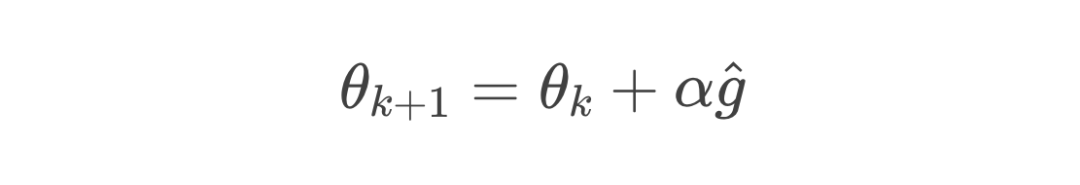

5. 循环优化

-
这里,我们利用大量实战(蒙特卡洛抽样)来近似整个期望。 -
轨迹总奖励 就是整盘棋的胜负结果,用来衡量你所有决策的综合效果。
2. 参数更新规则
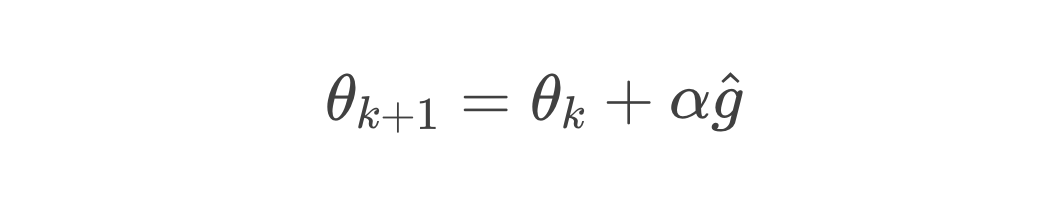
-
表示学习率,相当于每盘棋复盘后你调整策略的幅度;梯度的方向正是指向能够提升胜率的方向。
3. 算法特性
-
关键优势:这种方法完全依靠你下棋的实战经验,不需要提前知道对手的策略(model-free)。 -
计算要求:需要大量的对局采样以降低随机性带来的波动(方差)。 -
改进方向:后续方法(如 Actor-Critic)会引入价值函数参考线,使得策略更新更为稳定,就像在复盘中加入专业教练的点评一样,帮助你更快提高棋艺。
2.4 策略梯度优化面临的问题
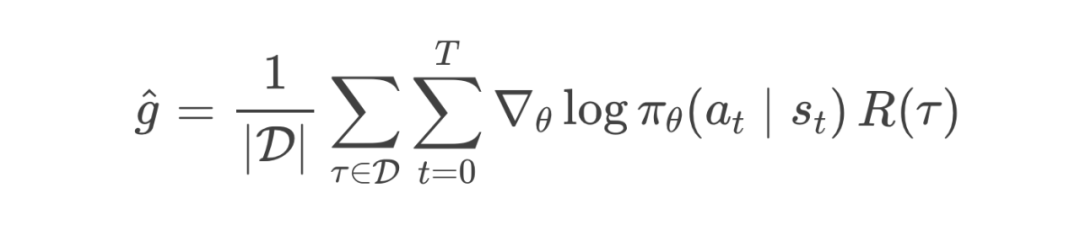
其中:
-
表示数据集 的大小, -
是当前策略(你的下棋策略), -
是整盘棋(轨迹 )的总回报, -
分别代表在时间步 你采取的动作和所处的状态。想象你在下棋。
2.5 减小方差:只关注未来
观察上边用于梯度估计得式子:无论当前在哪一步 , 总是会把整个轨迹中所有的 reward 都算进去。然后这么做是不太合理的,当前的决策应该只需要考虑对未来产生的影响:过去的已经无法改变了,无需再加入到 的计算中。
回到下棋的例子:假如每一步的评分都把前面已经走过的好步或坏步也计入进去,那就会混淆你当前决策的真实价值。实际上,在评估当前走法时,你只需要关注从这一步开始直到局末的“后续表现”。这就是所谓的“rewards to go”,即只考虑从当前动作开始到比赛结束所获得的奖励。
用数学表达就是,我们将原来的梯度估计调整为:
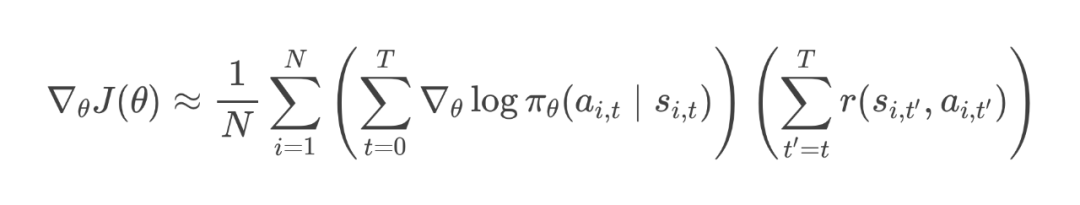
这里,就代表了从当前走法开始到局末的“奖励总和”。这样做就像你在复盘时,只关注从某一步开始后续的变化,而不纠结于那一步之前已经发生的事情。
因此,当我们把这些“来自过去的”的冗余项去除后,噪声就自然而然会减少一些。
2.6 减小方差:参考线(Baseline)
为了进一步减少评估中的波动,我们可以为每一步的“后续奖励”减去一个基准值。数学上,这个参考线通常记为 (在实际中,我们常用价值函数 来作为这个参考线),公式为:
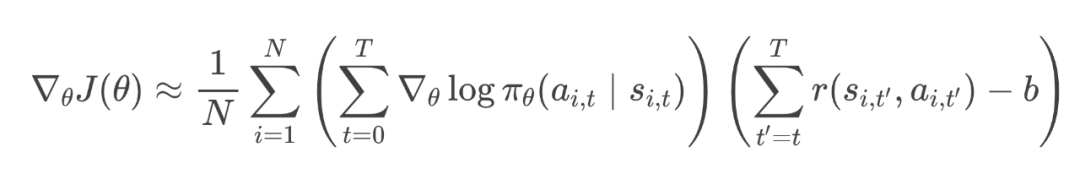
其中 就是所谓的参考线,他不一定是一个常数,更多时候是另外一个状态 的函数。这个参考显得实际意义是,在当前的状态下,回报的期望大概是什么样子。那么所谓超出期望的部分 就是优势(Advantage)。在实际训练中,我们会用优势代替原来的奖励进行梯度估计,以减小方差。
在大语言模型的对齐训练中,我们通常在语言模型(即策略 )的基础上增加一个额外的线性层,用来估计在某个状态下的预期回报 。这相当于为每个局面设定了一个标准分,帮助我们衡量当前决策的实际优势。如果你想更直观得了解为什么需要这个参考线,可以阅读我的上一篇文章。
2.7 减小方差:引入 和
在上边,我们提到了 “rewards to go” 的概念,即 。这个项在强化学习中被称为 Q 函数(),即在状态 采取动作 后,未来获得的总回报。然后,通过减去状态价值 我们得到优势函数:

用下棋的比喻,Q 函数描述的是你当前这个局面 在走了一步 后可能的输赢,而状态价值表示的是仅凭现在的局面,你还有多少老本儿可以吃。如果当前局面对你十分有利,但是你走了一步臭棋,尽管你最后赢面还是很大(相当于 的绝对大小还是很大),但是你相对于对方的“优势”却减弱了。
所以,你不仅应该关注某一步棋的绝对得分,还要和“老本儿”比较比较,看看这一步棋究竟为你增加了多少胜率。如果 为正,则说明这步棋明显扩大了你的优势;若为负,则表明你这一招不妙。
最终,我们可以将策略梯度写为:
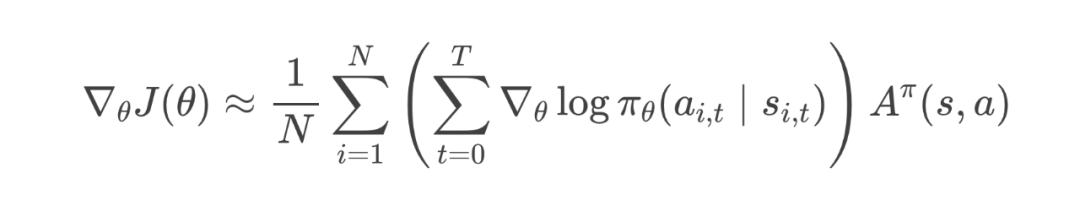
2.8 优势函数的解释
简单来说,优势函数 就告诉你,在某个局面(状态 )下,选择某个特定走法(动作 )相比于平均走法能提升多少胜率。如果这步棋带来的预期回报远高于你当前的基准水平,那么这步棋的优势就是正的,说明它非常值得采用;反之,则说明不如平均水平。
总之,通过这些方法——只考虑“后续奖励”、引入参考线以及使用优势函数,我们就能在训练中有效降低梯度估计的方差,就像你在下棋时只关注关键走法对局面转变的影响,从而让策略更新更稳定、更有针对性。
2.9 如何估计优势项 – 使用基于迭代的 GAE 策略
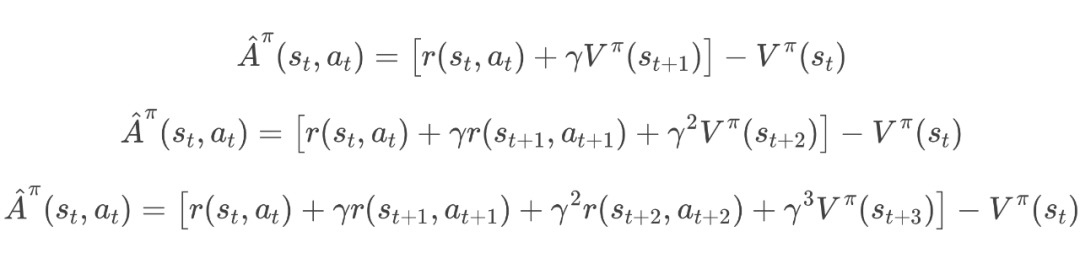
-
如果我们过早地停止累加真实的奖励项:就会产生高偏差(high bias),因为只使用了对价值函数的小部分近似和极少的真实奖励。 -
如果我们累加过多的奖励项:则会引入高方差(high variance),因为依赖更多真实采样会让估计量不稳定。
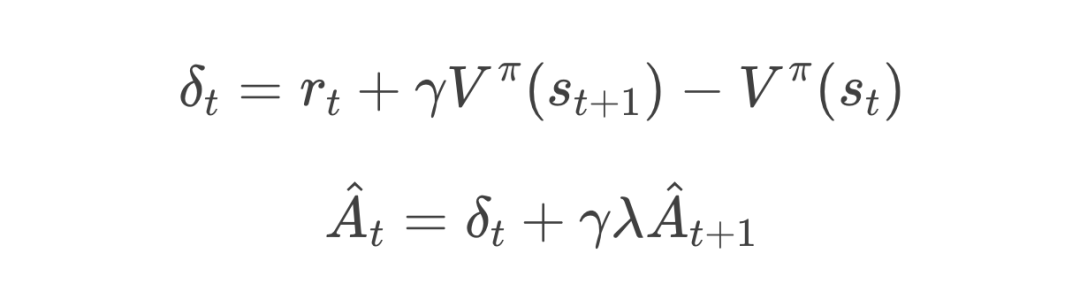
-
这是一个递归公式。末端时刻的优势估计可以看作第一种展开,而它的前一时刻会再加上一层衰减系数 。 -
通过在各时间步上不断迭代累加,就可以平衡真实奖励所带来的高方差和使用价值函数所带来的高偏差。
2.10 PPO 损失函数(The PPO Loss)
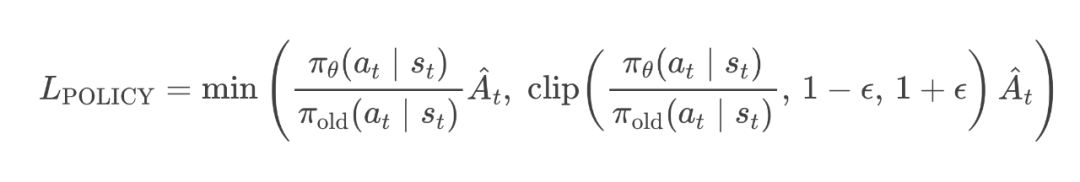

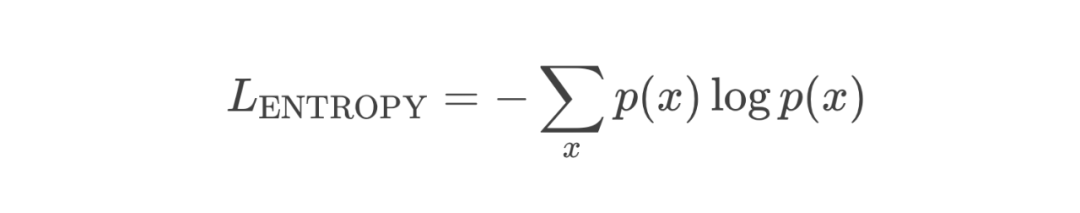
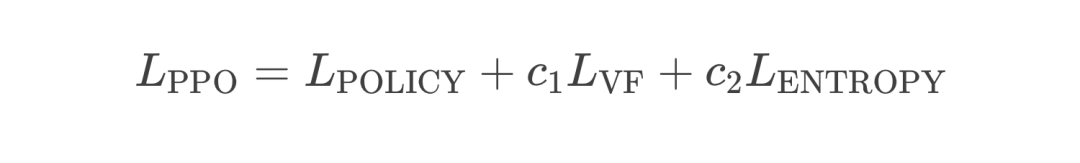
2.11 使用 PPO 的优势
-
稳定性:剪切操作(clipping)确保策略更新时步伐不会过大,就像你在下棋时不会突然改变风格,保证每一步都稳扎稳打。 -
样本效率:PPO 能够较好地利用收集到的对局数据,尽管在大型模型的场景下仍需大量采样。 -
内在安全性:通过剪切更新和参考策略的 KL 惩罚,PPO 能有效防止模型在更新时出现剧烈偏差,从而确保生成结果不会与预训练风格南辕北辙。

GAE(广义优势估计)理解及推导
3.1 引入残差的概念
为什么需要残差?
残差的数学表达
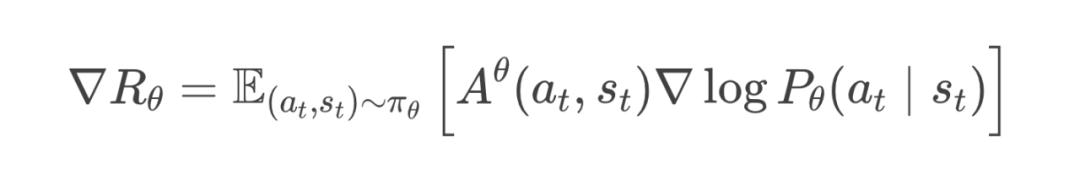
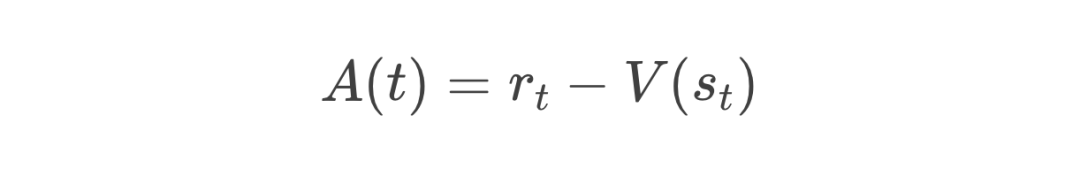
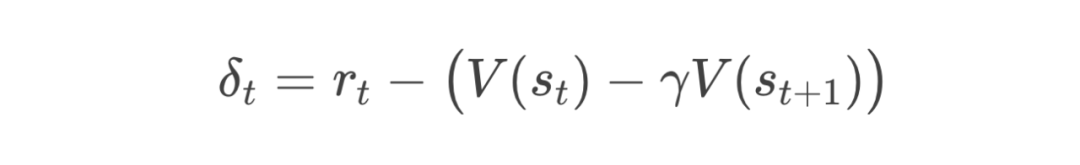
-
就像你下完这一步棋后获得的即时得分。 -
和 分别是你对当前局面和下一局面预期的整体评分,相当于教练对局面的评价。 -
是折扣因子,表示未来奖励的重要性逐步减弱。
残差的直觉解释
-
你对当前状态 的预估价值是 ,它代表你在这个状态下按照当前策略继续走下去能获得的预期收益。 -
你对下一步 的预估价值是 ,它代表你在下一步之后能获得的预期收益。

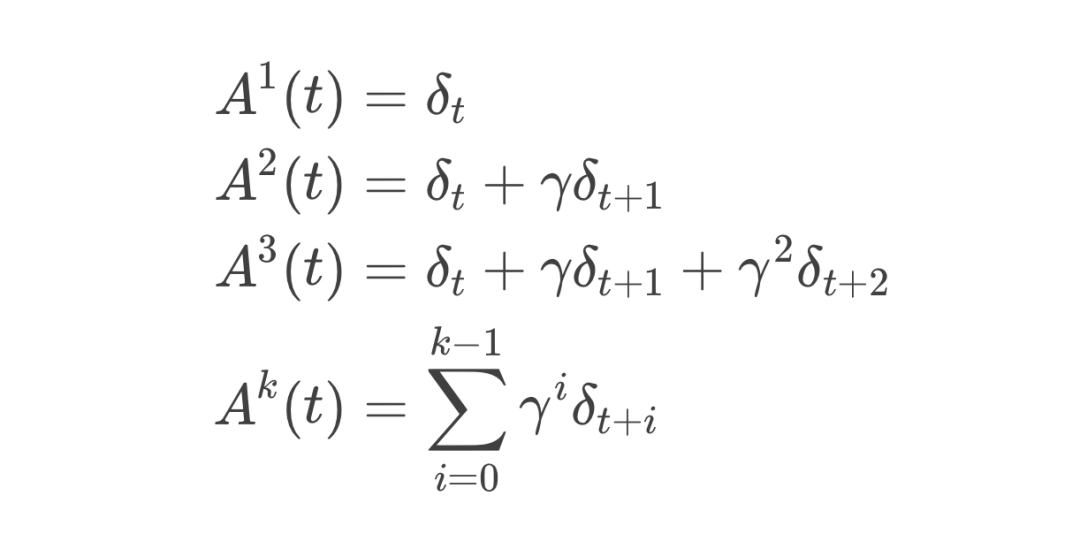
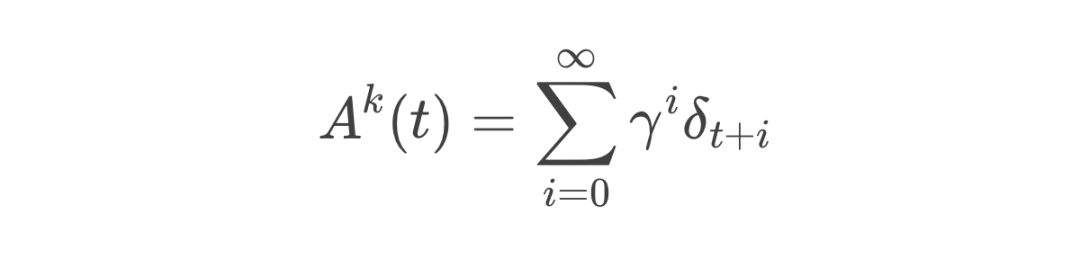

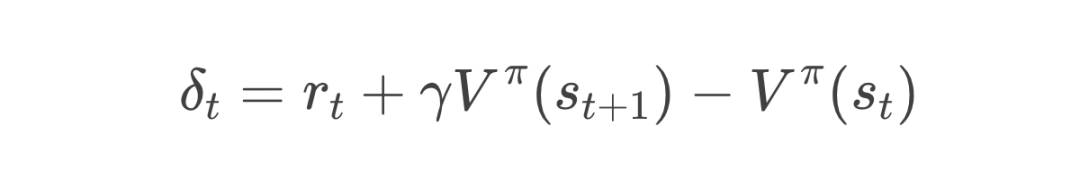
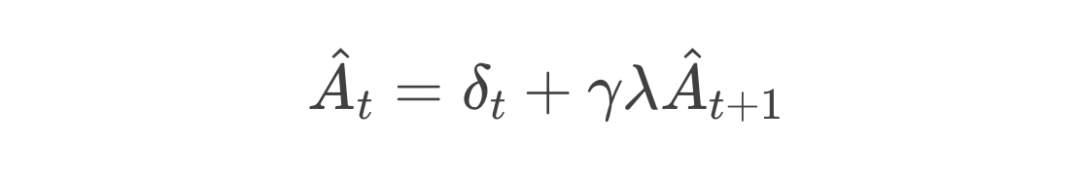
-
当 时,你会尽可能考虑整盘棋的所有后续效果(偏差最小,但方差最大)。 -
当 时,你只关注当前一步(偏差最大,但方差最小)。
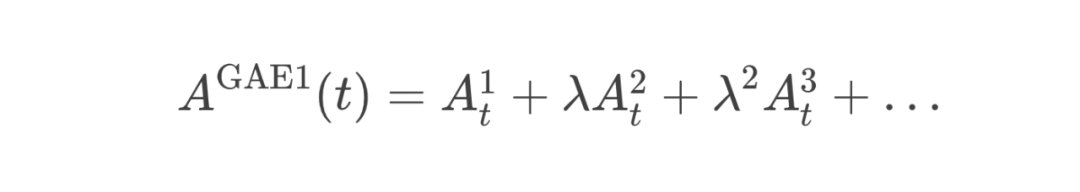
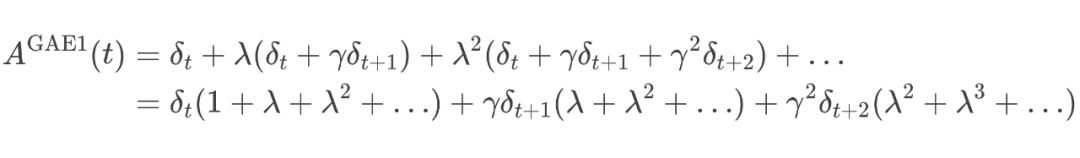

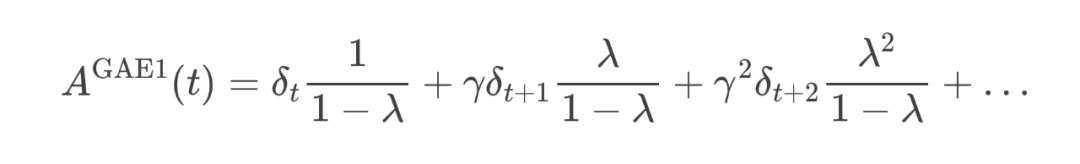


-
当 时,优势估计包含了整盘棋的所有观察信息(偏差最小,方差最大): 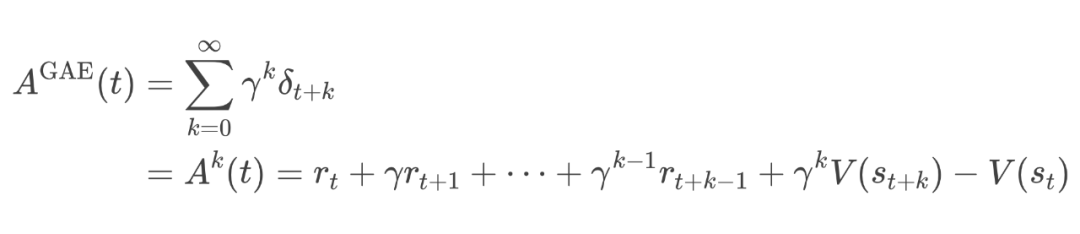
-
当 时,只依赖于当前一步的信息(偏差最大,方差最小): 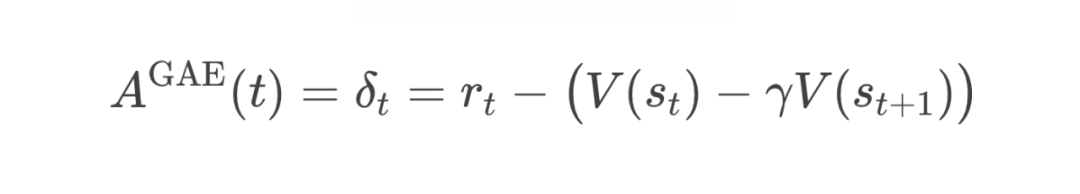
-
越大,考虑的后续观察越多,偏差越小,但方差越大; -
越小,依赖当前预估越多,偏差越大,但方差越小。

用 PPO 训练 LLM 的 Token-per-Token 过程
下面以一种直白、逐 token 的方式讲解在使用 PPO 训练一个 LLM 时到底发生了什么,并说明其中涉及的参数( 与 )的角色以及第一次更新的过程。
4.1 用 PPO 对齐 LLM
-
(旧策略参数):这是用来生成数据(比如生成 token 序列)的模型参数。在一次 PPO 更新前,你会用这套参数来采样(即生成 token),同时记录下每个 token 的生成概率(通常以 log-probability 的形式记录)。 -
(当前策略参数):这是正在被更新的模型参数。你通过 PPO 算法根据之前采样得到的数据来调整这组参数,使得模型生成的 token 更符合奖励信号。更新后, 就会和 不一样。
可以把 想象成“老版模型”,而 则是“新版模型”,新版模型在一次训练迭代后会比老版模型更好(或者更符合奖励信号)。在每次更新后,新版模型会成为下一轮循环中的“老版模型”。
2. “Token-per-Token” 的训练过程
模型根据当前上下文(state)生成下一个 token(action)。例如,当生成第 t 个 token 时:
-
当前状态 是 prompt 加上前面 t-1 个 token。 -
模型选择了 token 的动作,并给出了一个概率 (通常记录为 log-probability)。
对于每个 token,你记录:
-
状态 (上下文) -
动作 (生成的 token) -
旧策略下的生成概率(或 log-prob) -
可能还会记录奖励信息(比如通过一个奖励模型计算出的分数)和估计的价值 。 -
这样形成一条轨迹(sequence)——一系列 token 及其相关数据。
-
举例:对于第 t 个 token,我们可能计算:
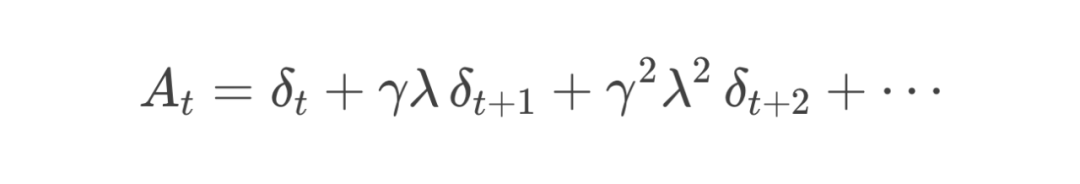
-
其中 是单步时序差分误差。 -
在实际操作中,由于轨迹有限,我们只计算到轨迹结束的位置。
在采样得到一批 token 数据后,你开始用 PPO 算法更新模型参数。这里 “token-per-token” 的解释如下:
1. 旧策略作为参照
2. 当前策略重新计算概
3. 计算概率比
对于每个 token,计算概率比:

这个比值表示“新版模型”与“旧版模型”在该 token 处的生成倾向发生了多大变化。
4. 构造 PPO Loss(每个 token 的损失)
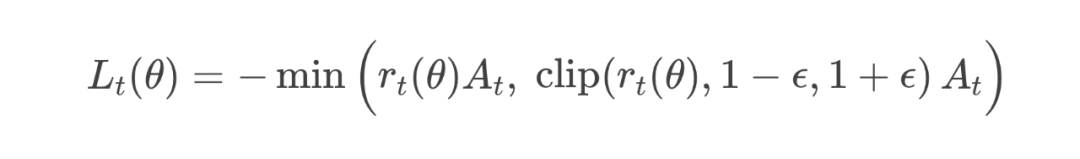
直白理解:
-
如果当前策略与旧策略的概率比 和优势 的乘积在可接受范围内(在 内),就用这个值。 -
如果比值太大或者太小,就用限制后的值(clip 后的值),防止更新步长过大。
-
这时, 开始和 不一样了,也就是说新版模型已经从旧版模型上进行了“改进”。
下面给出一个伪代码风格的算法块,帮助理解 token-per-token 的 PPO 更新过程:
# 初始化:预训练 LLM 的参数设为 θ_old,同时复制给 θ
θ_old = PretrainedLLM.parameters
θ = copy(θ_old)
# 采样阶段:使用 θ_old 生成一批数据
for each prompt in dataset:
trajectory = []
state = prompt
while not end_of_sequence:
token, logpi_old = θ_old.generate_token(state)
# 记录当前状态、token 以及 θ_old 下的 log概率
trajectory.append( (state, token, logpi_old, reward, V(state)) )
state = state + token # 更新状态(追加 token)
store trajectory
# 计算优势(例如采用 GAE)
for each trajectory:
for t from last token downto first:
δ_t = reward[t] + γ * V(state[t+1]) - V(state[t])
A_t = δ_t + γ * λ * A[t+1] # 递推计算
# PPO 更新阶段:多轮 epoch
for each PPO update epoch:
for each token data (state s_t, token a_t, logpi_old, A_t) in batch:
# 1. 当前策略计算 log 概率
logpi_current = θ.log_probability(s_t, a_t)
# 2. 计算概率比
r_t = exp( logpi_current - logpi_old )
# 3. 计算未剪切与剪切目标
loss_unclipped = r_t * A_t
loss_clipped = clip(r_t, 1-ε, 1+ε) * A_t
# 4. 每个 token 的损失取较小值(并加上负号,因为我们是最小化 loss)
loss_token = -min(loss_unclipped, loss_clipped)
# 5. 平均所有 token 的 loss,进行一次梯度更新
θ = Update(θ, average(loss_token over batch))
# 更新完毕后,将 θ 复制给 θ_old,用于下一轮采样
θ_old = copy(θ)

-
是新模型(参数 )与旧模型(参数 )在相同状态下生成同一 token 的概率比, -
是优势估计,反映了该 token 相对于基准(baseline)的“好坏”。
2. 如果新模型和旧模型一模一样,损失是不是为零?
-
在第一次更新之前,我们通常将新模型参数 初始化为旧模型参数 。因此,对于每个 token, 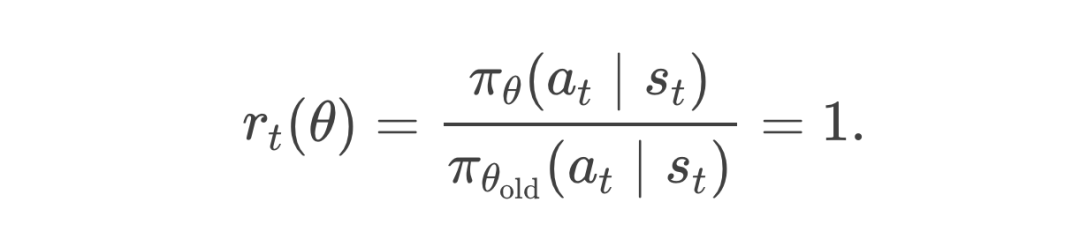
-
代入 PPO 目标函数,两项都会变为: 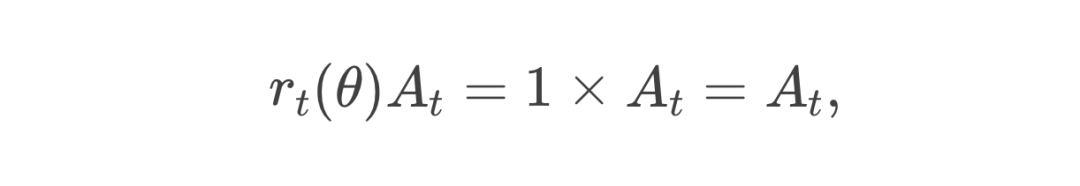
并且剪切操作对 1 没有影响(因为 ),结果仍然是 。 -
因此,每个 token 的目标函数就是 ,而 Loss 是加上负号,即: 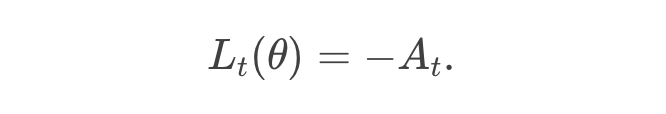
-
采样阶段
当你用旧模型()生成 token 时,会记录每个 token 的生成概率、对应的奖励以及基于价值函数的估计。假设某个 token 在环境中获得了较高奖励,但模型当时对该 token 的预估不够乐观,那么它的优势 就是正的;反之,如果奖励低于预期,优势 就可能为负。 -
第一次更新 尽管初始时 与 完全一致(所以概率比 ),PPO Loss 的计算主要依赖于优势 。因此,Loss 为: 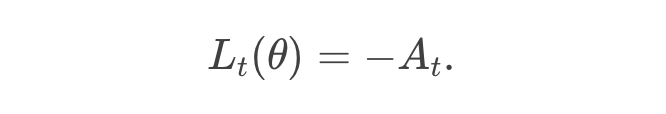
如果 为正,则负号意味着 Loss 为负,反向传播时会鼓励模型增加生成这个 token 的概率;如果 为负,则模型会减少生成该 token 的概率。 -
梯度更新的作用 这样,尽管新旧策略当前一致,优势 的非零值会通过梯度计算推动模型调整生成策略,从而在下一次生成时更倾向于产生正优势的 token。
-
PPO Loss 的核心目标:
不是直接对比新旧模型参数的差异,而是基于旧策略采样数据上每个 token 的优势来指导模型更新。 -
即使在第一次更新时:
由于优势 通常不为零,PPO Loss 会产生非零梯度,从而促使模型在更新过程中调整策略,使其生成结果更符合奖励信号。

DPO:看着棋谱学下棋
-
ward Model Loss:

-
PPO Loss:
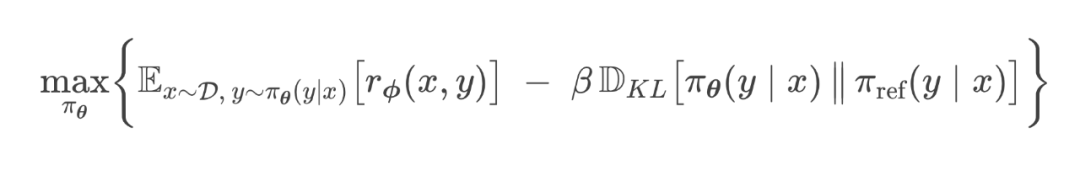
-
DPO Loss:
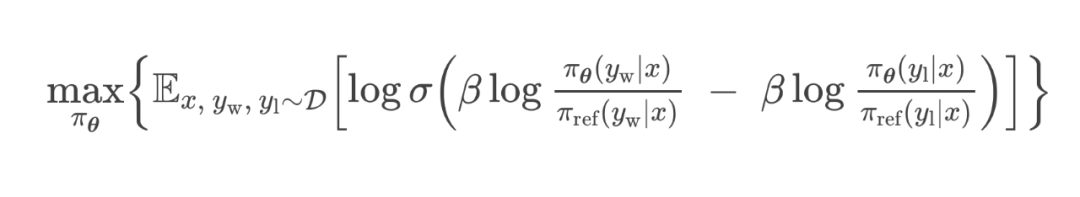
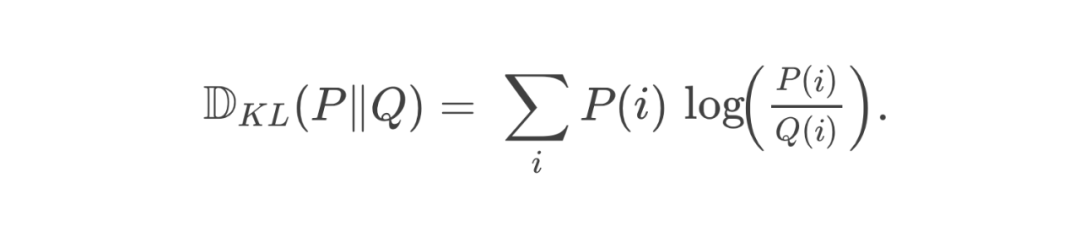
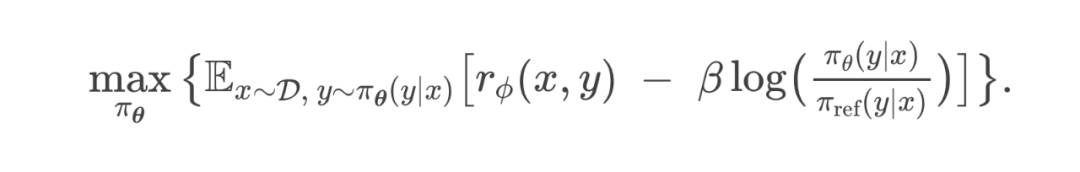
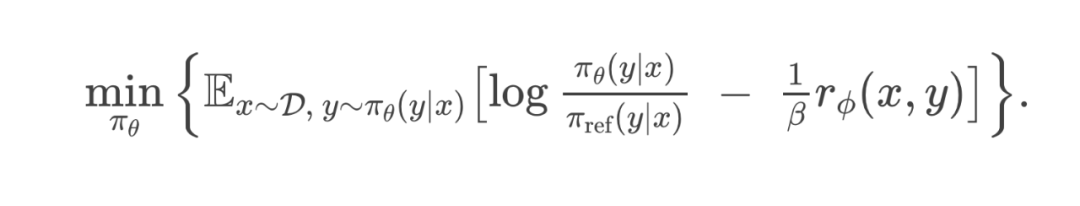




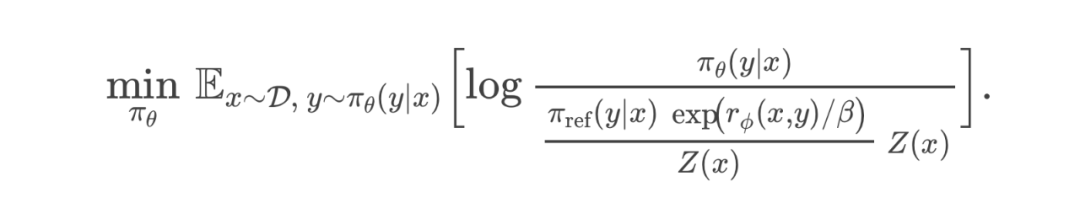





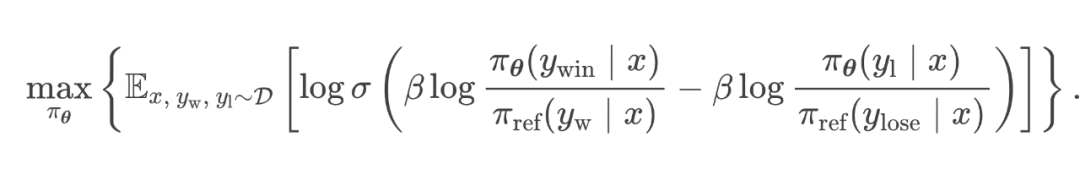



5.2 跳过奖励模型的训练

-
很难估计:它需要对给定 prompt 下的所有回答 进行穷举或采样,计算 并累计,代价十分高昂。 -
我们最初目标是想绕过“先训练奖励模型”这一步,直接一步到位地学出一个对齐模型。然而 仍需已知 ,离我们想要的“直接学好棋”(而不是先学打分)还有距离。

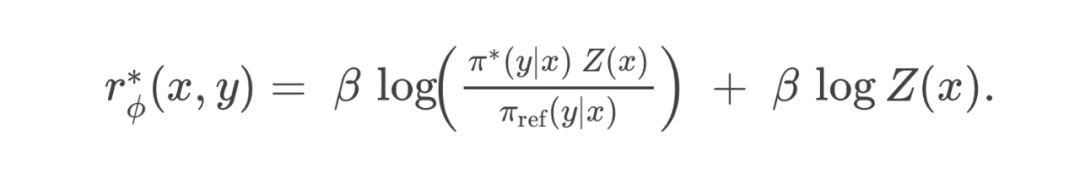
总结这一部分:

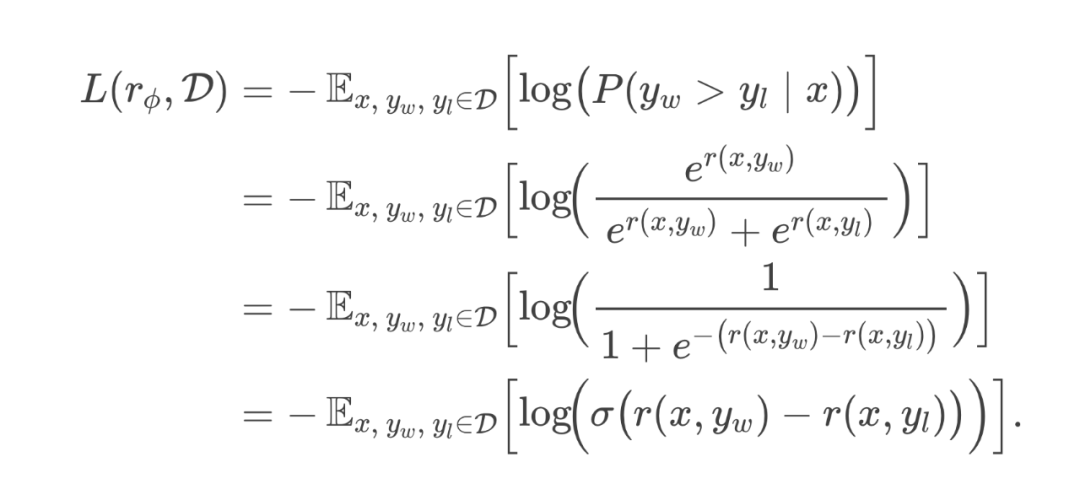


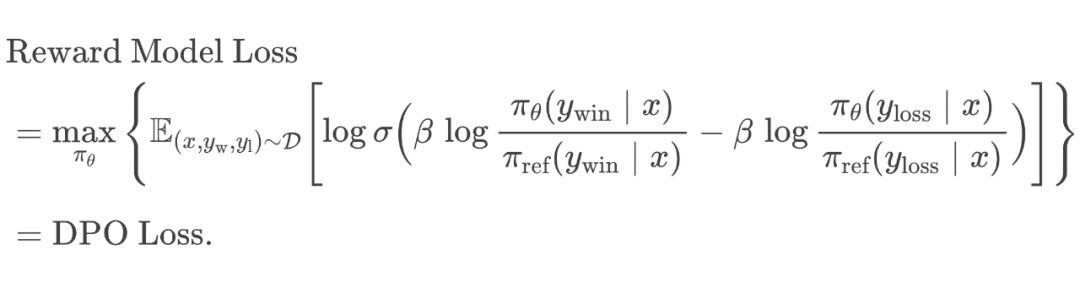
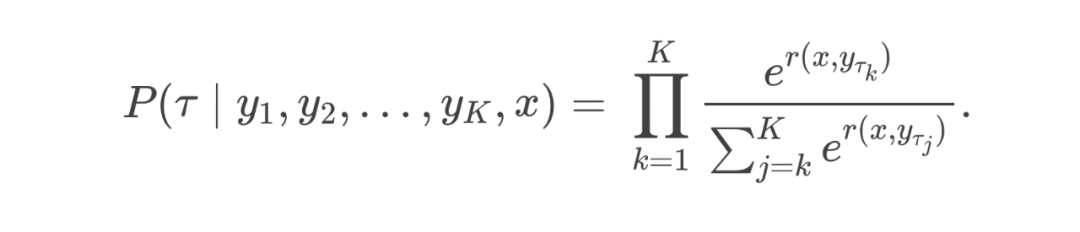


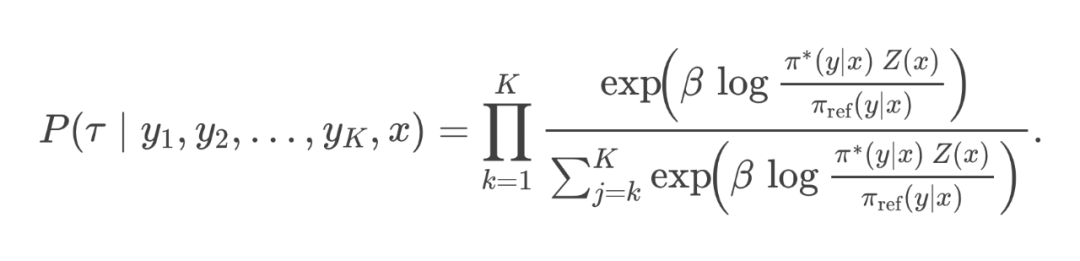
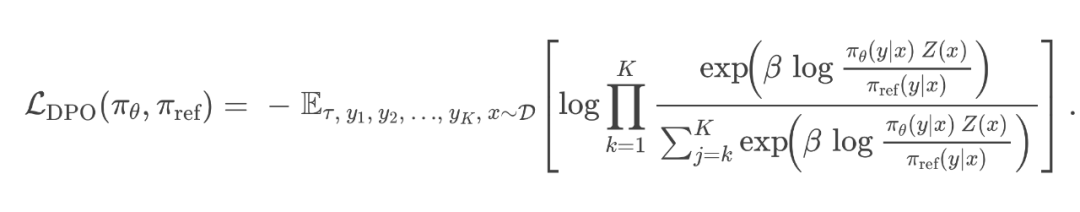
(文:PaperWeekly)

