PPO & GRPO原理，小学生也能看懂！

 Datawhale分享 

作者：小天狼星不来客

作者：小天狼星不来客，欢迎持续关注作者博客

来源：https://zhuanlan.zhihu.com/p/22128744640，仅用于学术分享

01

开篇

在强化学习（RL）中，如果我们只知道“做对了能拿多少分”，那往往还不够，因为单纯追求高分可能带来种种副作用，比如过度搜索、模型不稳定、甚至“走捷径”而偏离合理范围。

为了解决这些问题，人们在 RL 中设计了许多机制——Critic（价值函数）、Clip 操作、Reference Model、以及最近流行的 GRPO（Group Relative Policy Optimization）等。

为了把这些概念讲得更生动，我们不妨打个比方：把 RL 模型的训练过程想象成小学里的考试场景。

我们（被训练的模型）就像努力考高分的学生，发奖品的人则像 Critic 或者其他调控机制。

接下来就让我们循序渐进地看看，为什么只靠最终成绩是不够的，为什么需要一步步引入 Critic、Clip、Reference Model，最后又是如何引出 GRPO 的思路。

02

只有 Reward 时的朴素做法：为什么会有问题

假设我和我弟弟都在小学同一个班上课。老师改卷后给出一个“绝对分数”，我的成绩一般 80 分以上，弟弟成绩大概 30 分左右。

然后我们把这个分数直接拿去找爸爸要零花钱——也就是用“分数本身”作为奖励（Reward）。谁考得分数高，零花钱就多。

一开始听上去没毛病，但结果就有两个问题：

• 不公平：如果弟弟从 30 分进步到 60 分，付出了非常大的努力，却依然比不过我平时随便考个 80+。他得不到有效激励。
• 不稳定：我为了冲刺高分，可能会采取极端学习策略（比如疯狂刷题、考前通宵），偶尔考到 95 分，偶尔只有 60 分，成绩大起大落，导致奖励信号也忽上忽下。

这样一来，只拿绝对分数当作 Reward，奖励信号波动很大，弟弟也会觉得不公平，久而久之，就没动力进步了。

数学对应

在强化学习里，如果我们只用：

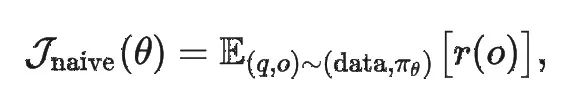
也就是“把最终 Reward 直接拿来做优化目标”，就容易出现高方差、激励不充分等问题。

换言之，Actor 得不到一个和自身水平相称的参考线(baseline)，进而影响学习效率。

03

引入 Critic：用“预期分数线”来改善奖励机制

针对上面的问题，爸爸很快意识到：“不能光看绝对分，而要看看每个人在自己水平线之上进步多少才是关键。”

于是爸爸决定：给我定一个“预期分数线”80 分；给弟弟定一个“预期分数线”40 分。考试时，只要超出自己那条线，就能得到更多零花钱；如果没有超出，那么零花钱就可能很少或者没有。

这样一来，弟弟如果努力从 30 分考到 60 分，超出自己预期分数线 20 分，就能得到可观的奖赏。

我如果还是 80 多分，增幅不明显，那就算分数比弟弟高，但并不一定多拿太多钱。

这样就鼓励了每个人以自己的水平为起点去进步，而不是一味比谁绝对分高。

当然，爸爸也很忙，不是说一旦定了分数线就一劳永逸——他得根据我们的学习状况来不断“自我调节”，因为如果弟弟水平已经到 60 分了，再给他设 40 分的线就不合理了。

反之，我要是一直考 85 分没什么波动，也可能需要微调我的分数线。 所以，爸爸也需要不断学习，只不过他需要学习的是我和弟弟的学习进度。

数学对应

有了这个“分数线”去做差，我们能降低训练过程中的方差；也让高于预期的动作拿到更大的梯度，低于预期的动作被抑制。

04

加入 Clip 与 min 操作：防止更新过度

有了“分数线”以后，效果确实好了很多。

但新的问题出现了：如果某一次考试我突然爆发，进了高分段，比如 95 或 100 分，爸爸会给我极高奖励，导致我在下一次考试前可能“走火入魔”，去尝试各种极端学习方法，成绩忽高忽低，奖励也随之剧烈波动。

为此，爸爸觉得要适度控制我更新学习策略的“步幅”——一次性冲太高也不一定要给我成倍加零花钱。给得太多，会让我产生极端探索心态；给得太少又会抑制热情。总之需要一个平衡。

数学对应

在 PPO(Proximal Policy Optimization)中，这个“平衡”靠“Clip” 操作来完成。

我们常见的 PPO 核心目标函数里，有这样一段：

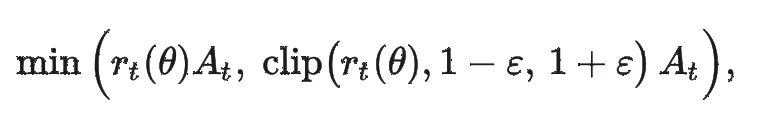
其中：

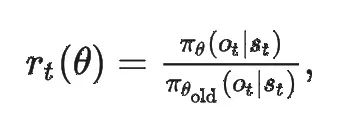
表示新策略与旧策略在这个动作上的概率比值。如果这个比值离 1 太远，就会被 Clip 在【1-ε，1+ε】区间内，从而限制一次更新幅度别过大。

用故事的话讲，就是：我考到 100 分，可以多拿奖励，但爸爸会有个“封顶”的约束；下一次还要观察一下再做决定，这样保持学习的平稳性，防止出现一条极端的“歪路子”。

05

Reference Model：防止作弊、极端策略

即便如此，如果我为了追求高分，不惜采取非常规手段——比如考试作弊、威胁老师改卷之类，那不就轻松拿下满分了吗？

这显然是违反原则的。而且如果在语言模型场景，可能出现生成有害言论、编造事实等“走歪”的行为。

于是爸爸又提出一个附加约束：“无论如何，你不能偏离最初正常学习的方法太多。否则即使你考了高分，我也判你不合格，零花钱也不给。”

这就好比我们在学期开始（也就是监督微调后）的“合规”状态那里画了一条“参照线”，新的行为不能和这个初始策略差太远，否则就要受到惩罚。

数学对应

06

GRPO：用“多次模拟成绩平均值”代替价值函数

有一天，爸爸说：“我没空天天衡量你的学习水平了，不想再手动给你画分数线。那你干脆先把试卷做 5 份模拟题，取这 5 次的平均分，这个平均分就是你的预期分数。真正考试时，如果你比这个平均分高，就说明你表现超出你自己的期望，我就给奖励；不够的话，说明你的表现没到平均线。” 

如此一来，弟弟、我，甚至更多同学都可以用“自己多次模拟考试”的均值来做分数线，不需要依赖一个外部（爸爸）不断微调的“价值网络”。

前面几个环节，我们已经看到了 PPO 的思路：Actor + Critic + Clip + KL 惩罚。

但在实际应用尤其是大型语言模型（LLM）上，Critic（价值函数）通常需要跟 Actor 同等大小的网络去估计，否则很难评估到位，成本很高，而且有些场景（比如只在回答末尾才有一个整体 Reward）并不太适合训练出精细的价值函数。

这时候就出现了 Group Relative Policy Optimization（GRPO）。

它的要点是：不用“学习”一个单独的价值网络当 Critic；而是对同一道题目、同一个状态，先用旧策略采样多条输出，然后把这些输出的平均 Reward 当作 baseline； * 超过平均值就相当于“正向 Advantage”，低于平均值就是“负向 Advantage”。

在 GRPO 里，除了这一步，还保留了PPO 中的 Clip 和对 Reference Model 的 KL 正则，这些都可以保障更新的稳定性和合规性。

数学对应

DeepSeekMath 的技术报告里给出了 GRPO 的目标函数（省略部分符号细节）：

07

结语：回顾与展望

通过这个小学考试的比喻，我们逐步从只看绝对分数的朴素思路，演化到 PPO 的完整机制（Critic、Advantage、Clip、Reference Model），再到 GRPO 的创新思路（用一组输出的平均得分当基线，省去价值函数的繁琐）。

以下几点值得再次强调：

• Critic 的意义：它为每个状态或阶段提供“合理预期”，大幅降低了训练方差；

• Clip & min 机制：约束策略更新幅度，避免一次考试“爆发”带来的巨幅震荡；

• Reference Model：限制“作弊”或极端行为，让策略不要过度偏离最初合规范围；

• GRPO 的优点：在大型语言模型中，省掉了价值网络，减少内存和计算负担，还与“对比式 Reward Model”天然契合。

就像爸爸改用“让孩子自己多次模拟，然后以平均分当预期线”的思路一样，GRPO 让我们不用再额外维护一个庞大的 Critic，也能获得类似的相对奖励信号。

从结果看，这既保持了 PPO 原有的稳定性和合规性，又让训练更直接和高效。

希望这篇文章能帮助读者更自然地理解 PPO 与 GRPO 的原理，也能在实践中有所启发。

一起“点赞”三连↓

（文：Datawhale）