-
论文标题：Revisiting Generalization Power of a DNN in Terms of Symbolic Interactions -
论文地址：https://arxiv.org/abs/2502.10162
本文就上述问题给出了初步的探索，从神经网络内在精细交互表征复杂度的角度来探索「可泛化交互表征」和「不可泛化交互表征」各自所独有的分布。
一、大模型时代呼唤更高效的泛化性分析策略——中层表征逻辑的交流与对齐
尽管深度学习基础理论近年来取得了长足的发展，但一些根本性问题仍未得到有效解决。典型地，对神经网络泛化性的研究依然停留在一个相对较浅的层面——主要在高维特征空间分析解释神经网络的泛化性（例如通过损失函数景观平滑度来判断泛化性）。
因此，我们始终无法对神经网络泛化性给出一个「究竟」的解释——究竟怎样的确切的表征才叫高泛化性的表征。
然而，不同于判断「人工神经网络」的泛化性，人们对自身「生物神经网络」可靠性的有一种更加直接有效的评价策略——在内在表征层面的交流。让我们跳出不言自明的直觉，反观人类智能，其实人类的交流是一种很神奇的能力，两个上百上千亿神经元的黑盒大脑（而且链接方式也各不相同）居然可以不约而同地共享相同的底层符号化认知——不仅包括语言，还包括一些下意识的公共认知（比如底层的 image segmentation 都是下意识自动完成的），让人们可以直接可以从中层逻辑层面进行交流和对齐。人类彼此通过交流中层表征逻辑层面来实现对齐和互信，而不是像对待神经网络那样，需要通过长期的、大样本的、统计上的正确率来证明其可靠性。
比起端到端评测中统计意义的正确率，通过中层表征逻辑的交流，是判断一个智能体表征可靠性的一个更直接、更高效、更本质的手段。
二、两个本质的数学问题
然而，上述在中层精细表征逻辑上的交流与对齐，目前并没有被应用在人工神经网络上，根本上，工程实现上种种细节问题都可以归结为两个基本的数学问题。
问题 1：能否数学证明神经网络内在复杂混乱的各种精细表征逻辑，可以被清晰地、简洁地解释为一些符号化的概念。
这里，我们要面对一个看似相互矛盾的「既要又要」，既要解释的「简洁性」又要同时兼顾解释的「全面性」——用简洁的符号化操作解释神经网络中几乎全部的细节表征变换。
实验室前期提出的「等效交互解释理论」部分解决了上述问题。它证明了大部分神经网络的分类置信度的计算可以等效表示为一个符号化的（稀疏的）「与或交互逻辑模型」。
具体地，给定一个包含 n 个输入单元的输入样本，其一共存在 2^n 种不同的遮挡状态，我们发现神经网络在这 2^n 种不同遮挡状态下对目标类别的不同分类置信度，都可以表示为少量的（比如 50 到 150 个）与或交互逻辑的数值效用之和。
即无论输入样本被如何遮挡，其各种变化的分类置信度都可以被这个「与或交互逻辑模型」中 50 到 150 个交互所全部拟合出来。我们将其称为交互的「无限拟合性」——这是一个很强的结论，在数学上保证了「神经网络内在精细表征逻辑可以被严格地解释为少量的『 与或交互概念』」。
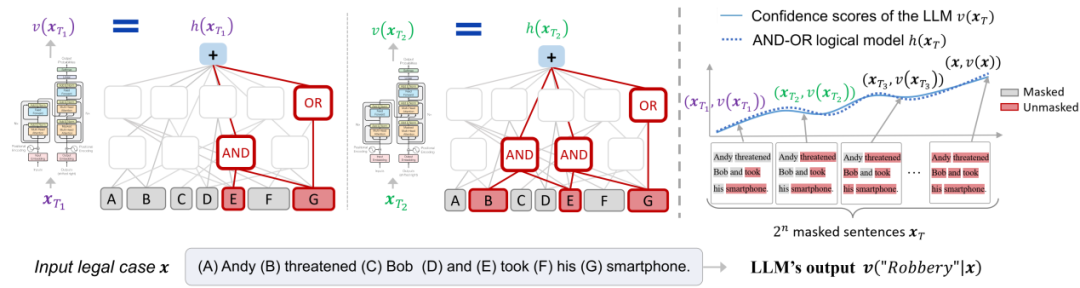
图 1. 与或交互的无限拟合性。给定一个神经网络，总能构造出一种稀疏的「与或交互逻辑模型」，仅使用少量的显著「与或交互」来精确匹配神经网络在所有 2^n 种遮挡样本上的输出。
如图 1 所示，「与或交互逻辑模型」中的交互分为「与交互」和「或交互」两类。其中，「与交互」S 表示神经网络所等效建模的输入单元间的「与逻辑」关系，当集合 S 内所有输入单元均出现在输入样本（不被遮盖）时，该交互为神经网络的分类自信分数贡献一个数值效应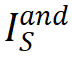 
。例如，图 1 中 LLaMA-7B 模型编码了一个与交互
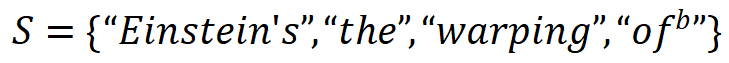，当集合内输入单元均出现时，为 LLM 预测下一个词素「space」（目标单词 spacetime 中的词素 token）贡献一个正的数值效应。「或交互」表示神经网络所等效建模的输入单元间的「或逻辑」关系，当集合 S 内任一输入单元出现（不被遮盖）时，该「或交互」为神经网络的分类自信分数贡献一个数值效应
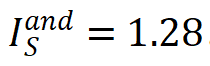。例如，上图中模型编码了一个或交互
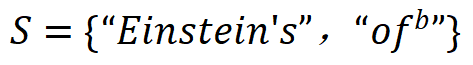，当集合内任一输入单元出现时，为 LLM 预测下一个单素「space」贡献一个正的数值效应
；
相关内容参考博客：
https://zhuanlan.zhihu.com/p/693747946
https://mp.weixin.qq.com/s/MEzYIk2Ztll6fr1gyZUQXg
三、通过符号化交互概念复杂度分布直接判断神经网络的泛化性
问题 2：我们能否直接通过神经网络所等效建模的符号化交互概念，直接判断神经网络的泛化性。
由于问题 1 已经在实验室前期工作中给出了理论解答，本文主要讨论解决问题 2——究竟能否在交互概念表征层面判断一个黑盒模型的泛化性，即我们能否从某个具体的数学指标，直接将神经网络的交互概念表征和神经网络的泛化性建立起内在的相关性。
由于我们证明了神经网络的分类置信度可以被解构为少量交互概念数值效用的和，所以神经网络整体展现出的泛化性可以被视为不同交互概念泛化性的集成效用。
交互泛化性的定义：如果一个交互概念在训练样本中大量出现，同时也在测试样本中也大量出现，那么我们认为这个交互概念被泛化到了测试样本。反之，如果一个交互概念只在训练样本中出现，而不在测试样本中出现，那么这个交互被认为是不可稳定泛化的。比如，在人脸检测中，神经网络往往建模两个眼睛和一个鼻子之间的交互概念，如果这样的交互概念在训练样本和测试样本上出现的频率是差不多的，那么这个交互概念就是可以稳定泛化的。
交互概念的阶数（复杂度）：交互概念 S 的复杂度可以由交互概念的阶数来量化，即交互概念 S 中包含输入单元的数目，i.e. order(S)=|S|。高阶（复杂）交互包含更多的输入单元，而低阶（简单）交互包含更少的输入单元。
交互概念的分布：对于所有 m 阶交互，我们通过计算所有 m 阶正交互的强度之和 和所有 m 阶负交互的强度之和来表示交互概念在不同阶数（复杂度）上的分布。具体计算公式如下
我们发现了，神经网络中不可泛化交互往往在不同阶数（复杂度）上呈现纺锤形分布，而可泛化的交互往往在不同阶数（复杂度）呈现衰减形分布。
以图 2 为例，大多数可泛化的交互是低阶交互，少部分是中高阶交互。此时可泛化的交互随着阶数升高强度逐渐减小，其在不同阶数上的分布呈现衰减形；而大多数不可泛化的交互主要是中阶交互，很少有极低阶交互和极高阶交互，而且每一阶的不同交互效用近似正负抵消。换言之，不可泛化的交互在不同阶数上的分布呈现纺锤形。
图 2. 我们发现神经网络的交互可以被分解为两部分：服从衰减形分布的可泛化的交互和服从纺锤形的不可泛化的交互
实验一：当我们训练神经网络直至过拟合，我们发现神经网络过拟合前的交互往往呈现衰减形分布，而过拟合阶段新出现的交互往往呈现纺锤形分布。
具体地，我们使用神经网络测试集 loss 与训练集 loss 之间的 loss gap 将神经网络的学习过程分成两个阶段：第一阶段，神经网络的 loss gap 趋近于 0，对应神经网络的正常学习过程。此时神经网络主要编码了低阶交互，交互的分布呈现衰减形，如图 3 所示。第二阶段，神经网络的 loss gap 开始上升，对应神经网络的过拟合过程，此时神经网络开始编码中高阶交互。我们使用
, 
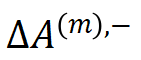分别表示神经网络在第二阶段过程中（相对于第一阶段末）所新编码的 m 阶正交互的强度之和和 m 阶负交互的强度之和。我们发现，在过拟合阶段神经网络新编码的交互呈现纺锤形分布。这印证了不可泛化的交互往往呈现纺锤形分布，而可泛化性的交互往往呈现衰减形分布的结论。
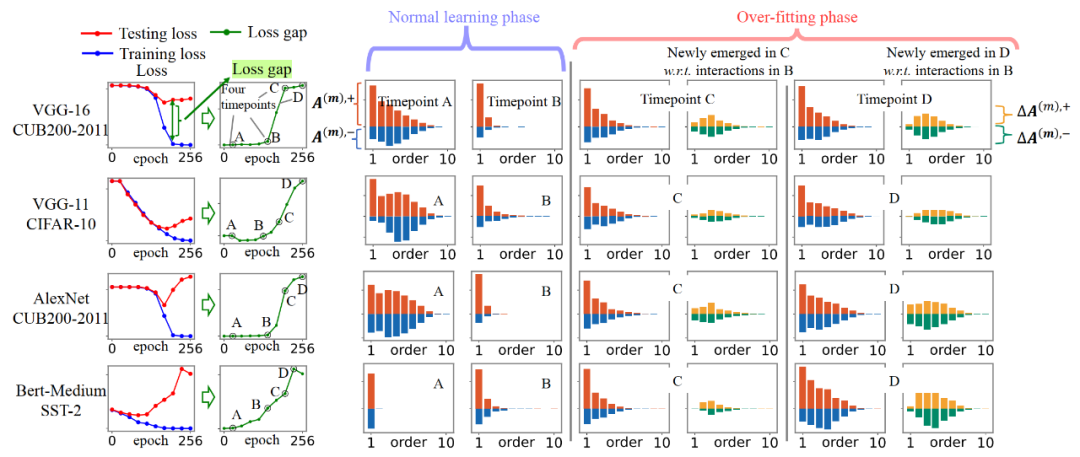
图 3. 交互在神经网络训练过程的两阶段动态变化过程。第一阶段，由模型参数初始化产生的噪声交互（时间点 A）被逐渐去除（时间点 B），神经网络主要编码了衰减形分布的交互。第二阶段，神经网络新编码的交互的分布呈现纺锤形（时间点 C 和 D）。
实验二：当我们修改训练好的神经网络，使其包含更多的不可泛化的表征时，新出现的交互往往呈现纺锤形。
具体地，给定一个训练好的神经网络，我们使用以下两种方法向神经网络注入不可泛化的表征：1. 向神经网络参数中添加高斯噪声，2. 向样本中添加对抗扰动。与实验一类似，我们使用, 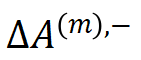表示神经网络在修改后相对于修改前所新编码的 m 阶正交互的强度之和和 m 阶负交互的强度之和。
我们发现，修改后新出现的交互的分布呈现纺锤形。此外，当我们逐渐增大所加入的噪声强度（方差），此时新出现的纺锤形分布的交互强度也逐渐增大。上述实验部分印证了不可泛化的交互的分布往往呈现纺锤形的结论。
图 4. 注入噪声后，新出现的交互分布（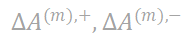
）呈现纺锤形。随着注入噪声强度的逐渐增加，新出现的呈现纺锤形分布的交互强度随之增大。理论估计的纺锤形交互分布（
）（见公式(6)）与实验测量的新出现交互分布高度匹配。
我们提出了两个参数模型来建模神经网络的不可泛化交互的纺锤形分布和可泛化交互的衰减形分布。
第一，对于纺锤形分布的建模，我们团队在之前的工作中发现了给定一个完全初始化的神经网络，此时神经网络编码的交互是无意义的高斯噪声。这时，可以证明给定完全初始化的神经网络，当输入单元的数量为 n 时，神经网络的 m 阶交互的强度和满足二项分布
。因此，在当前研究中，我们进一步发现对于一个训练过的神经网络，如果不是所有的输入单元之间都有交互时，我们可以引入比例系数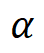
来构造如下参数模型来建模该模型不可泛化的交互的纺锤形分布。
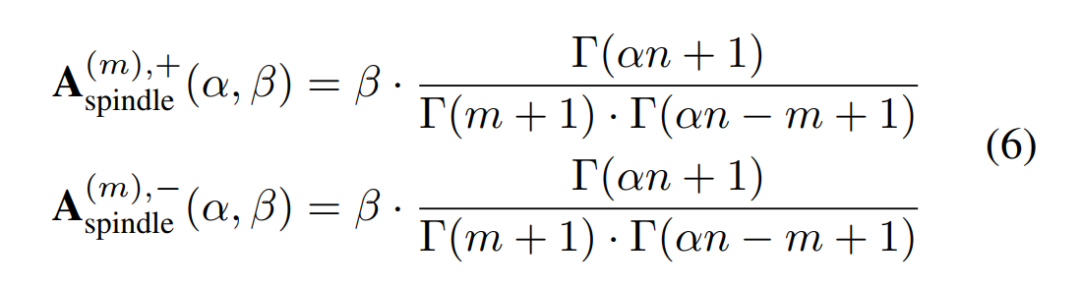
其中伽马函数
的作用是将阶乘拓展到实数范围
，进而实现了将二项分布
拓展到实数范围，即 
。
第二，对于衰减形分布的建模，我们团队在之前的工作中理论并实验验证了神经网络在训练过程的第二阶段的交互变化动态过程。定理 2.3 表示了神经网络参数和数据集中的不稳定噪声可以去除神经网络的相互抵消的中高阶交互，即避免过拟合。因此，我们可以通过设置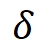
，来去除给定神经网络交互中的过拟合成分，从而得到衰减形分布的可泛化交互。
图 5 展示了在不同噪声强度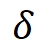下的理论交互分布和实际过拟合过程中的实际交互分布，结果显示定理 2.3 确实能有效预测过拟合前的交互分布。
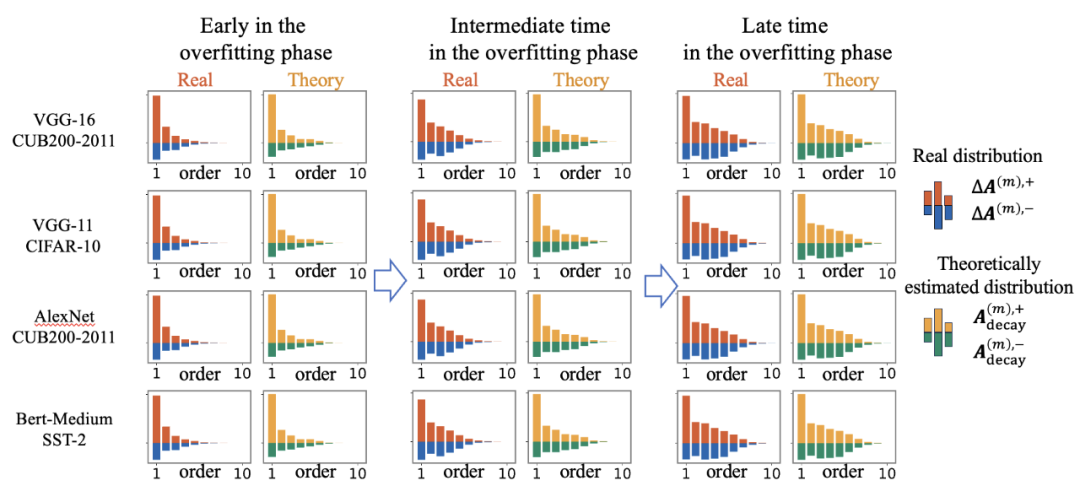
图 5. 比较神经网络的过拟合阶段的不同时间点点实际交互的分布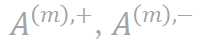
和理论交互的分布
。
因此，我们提出以下参数模型来建模神经网络可泛化交互的衰减形分布。
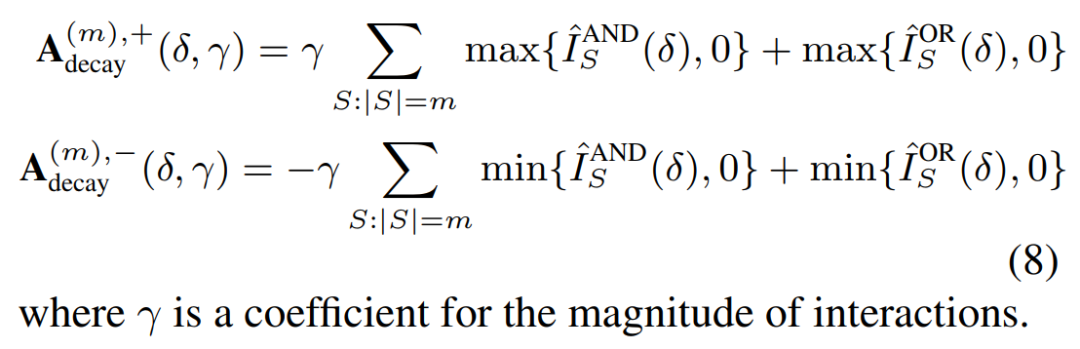
给定一个神经网络，我们提出算法将神经网络建模的交互的分布分解成服从衰减形分布可泛化交互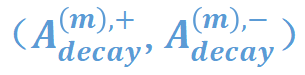
和服从纺锤形分布的不可泛化交互
两部分。
四、实验验证
实验一：验证纺锤形交互参数模型能精确匹配实际情景的不可泛化的交互分布。
具体地，在第三节的实验二中我们提出通过在神经网络参数上加高斯噪声以及在输入样本上加对抗扰动的方法为神经网络注入不可泛化的表征，我们发现注入不可泛化的表征后新出现的交互分布呈现纺锤形。结果如图 4 所示，可见我们提出的理论模型能精确匹配实际场景下的不可泛化的交互分布。
实验二：验证提取可泛化交互分布和不可泛化交互的分解算法的可靠性。
本实验中，我们同时提取神经网络建模的可泛化交互的分布和不可泛化的交互的分布。我们将从以下两个角度来验证算法的可靠性。
角度 1. 当我们往神经网络中注入更多的不可泛化的表征时，分解算法是否能精确提取出更显著的不可泛化交互分布和几乎稳定的可泛化交互分布。
角度 2. 我们使用拟合误差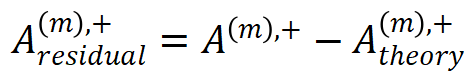
和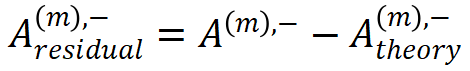 
来评估分解算法的拟合质量。
实验结果如下图所示，分解算法提取的不可泛化交互的纺锤形分布随着噪声增大逐渐显著，而可泛化交互的衰减形分布几乎不变。此外，拟合误差的相对强度较小，表明拟合质量较优。该实验验证了使用分解算法确实能有效提取神经网络的可泛化交互的衰减分布和不可泛化交互的纺锤形
图 6. 使用分解算法提取可泛化交互的衰减型分布
与不可泛化交互的纺锤型分布
。当我们向神经网络注入更多不可泛化的表征时，分解算法提取出了更显著的不可泛化交互分布和几乎稳定的可泛化交互分布。
实验三：在真实场景应用下使用分解算法提取可泛化交互的分布和不可泛化交互的分布。
具体地，我们在多个模型在多个数据集上使用分解算法来提取两种交互的分布。对于每个模型，我们选取了该模型在训练过程中的四个时间点，进而展示神经网络训练过程中可泛化交互的分布和不可泛化交互的分布变化。结果如图 7 所示
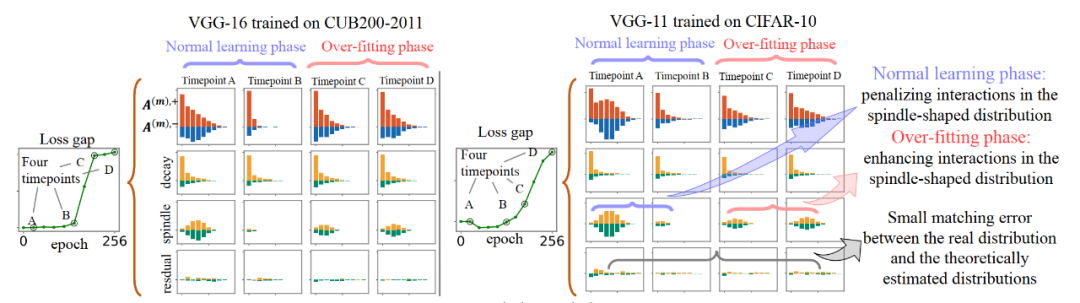
图 7. 使用分解算法从真实神经网络训练过程中的不同时间点提取可泛化交互的衰减型分布与不可泛化交互的纺锤型分布。在正常学习阶段，神经网络主要去除了纺锤形分布的交互，并学习了衰减形分布的交互。在过拟合阶段，DNN 进一步学习纺锤形分布的交互。
我们发现，在神经网络训练的学习阶段（此时 loss gap 几乎为零)主要消除了纺锤形分布的不可泛化的交互，这种交互来源于神经网络初始化引起的纯噪声。当学习阶段结束时，神经网络主要编码的是衰减型分布的可泛化的交互。
然后，在神经网络训练的过拟合阶段（此时神经网络的 loss gap 开始增加），神经网络又重新学习了纺锤形分布的交互。这表明神经网络开始编码不可泛化的正负相互抵消的中高阶交互，这对应了典型的过拟合现象。
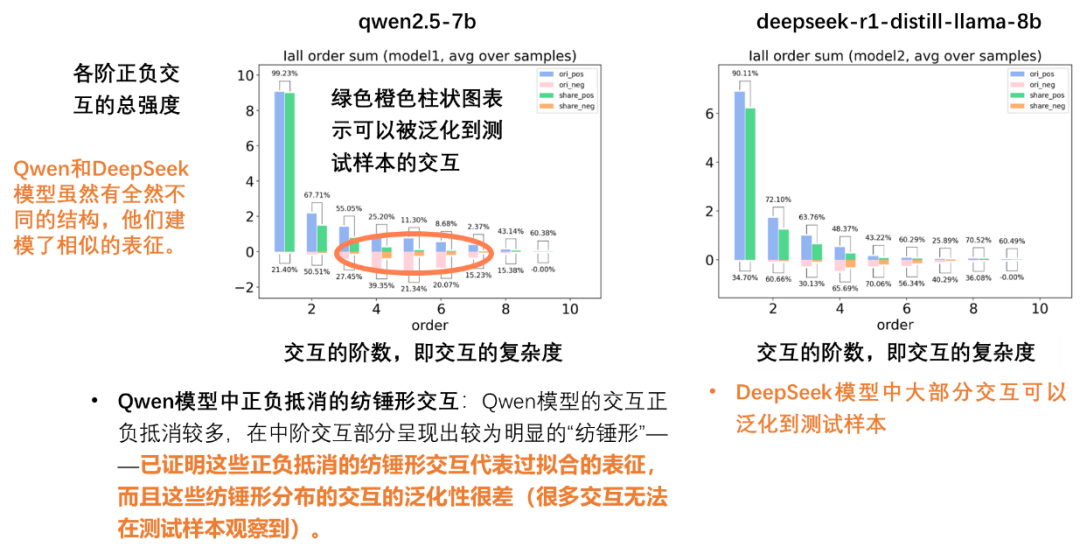
实验四：基于我们的理论，我们甚至可以解构出 Qwen2.5-7b 模型和 DeepSeek-r1-distill-llama-8b 模型的异同。
DeepSeek 模型中大部分交互可以泛化到测试样本。Qwen 模型的交互正负抵消较多，在中阶交互部分呈现出较为明显的「纺锤形」——这些正负抵消的纺锤形交互代表过拟合的表征，而且这些纺锤形分布的交互的泛化性比较差。
五、结论和讨论
我们通过神经网络所编码的交互概念的泛化能力来解释神经网络整体的泛化能力的根因。我们发现神经网络中可泛化的交互通常呈现衰减型分布，而不可泛化的交互通常呈现纺锤型分布。此外，给定一个神经网络，我们进一步提出了一种方法来提取神经网络编码的可泛化交互和不可泛化交互。
然而，我们的工作距离解释模型泛化性的终极理论还很遥远。我们仅描述了可泛化交互作用和不可泛化交互作用在复杂度上的总体分布趋势。然而，对于特定样本，理论依然无法从微观角度解释神经网络所建模的全部交互概念。
©
（文：机器之心）