克雷西 发自 凹非寺
量子位 | 公众号 QbitAI
不用引入外部数据,通过自我博弈(Self-play)就能让预训练大模型学会推理?
来自清华、北京通用人工智能研究院和宾夕法尼亚州立大学的研究人员,提出了一种名为“绝对零”(Absolute Zero)的训练方式。
这种方法通过让大模型根据推理目标,自己生成并解决任务,便可以获得推理能力。

测试中,用“绝对零”训练出的模型,表现已经超过了用专家标注样本训练的模型。
并且“绝对零”方法只需在代码环境中训练,但可以让模型在数学推理上也取得显著进步。
这项研究也在Reddit上引发了讨论,开帖转载的网友惊叹:会自我进化的AI已经被解锁了?

在出题-做题中自我学习
“绝对零”采用了一种自我博弈的学习范式。在这个范式下,一个统一的语言模型扮演Proposer和Solver两个角色。
Proposer负责生成新的推理任务,Solver负责解决这些任务。通过两个角色的交替和协同,模型可以自主地构建学习任务分布,并在求解任务的过程中不断提升推理能力。
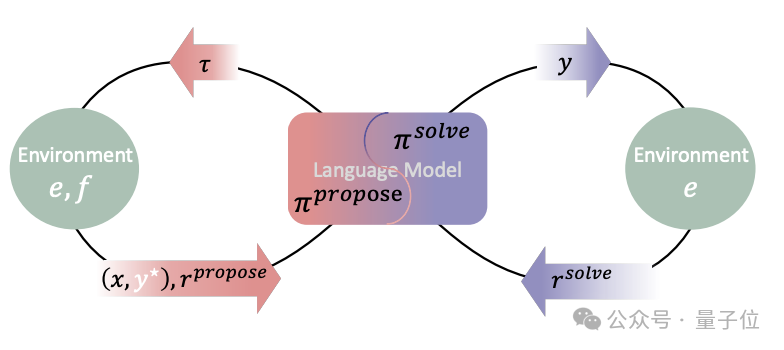
“绝对零”将所有的推理任务统一表示为(p,i,o)(即程序,输入,输出)的三元组形式。
这里的程序是一段可执行的代码,输入是该程序的输入数据,输出是程序在给定输入下的输出结果。
通过这种形式化的表示,原本抽象的推理任务被转化为了一个个具体的程序设计问题,语言模型可以通过生成和操作代码来完成任务的生成和求解。
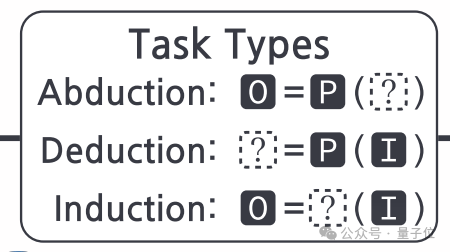
根据p、i、o是否已知,“绝对零”将推理任务划分为三种基本类型——溯因(Abduction)、演绎(Deduction)和归纳(Induction):
-
溯因任务:已知p和对应的o,求可能的i。这类任务考察模型根据结果反推条件、理解代码语义的能力。 -
演绎任务:已知p和i,求o。这类任务考察模型运行和理解代码逻辑的能力。 -
归纳任务:已知一组i-o样例,求一个统一p。这类任务考察模型归纳总结规律、生成代码的能力。
在自我博弈的训练开始前,“绝对零”需要一个初始的任务集合作为种子(如果基础模型足够强也可以不用)。这个种子集合通过基础语言模型生成一些有效的代码(p,i,o)得到。
当种子集合为空时,“绝对零”会使用一个预定义的“zero triplet”作为起点,实际上就是一个简单的恒等函数:
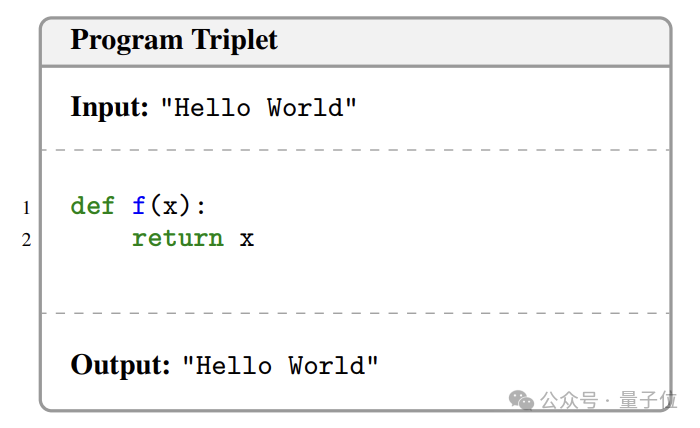
在每一轮迭代中,Proposer首先根据当前已有的任务集合和给定的任务类型,生成一个新的推理任务。
具体来说,它会先从历史任务中采样一些相关的例子作为参考,然后利用语言模型的生成能力,产生一个新的(p,i,o)三元组。
-
对于abduction任务,需要生成p和o,但不生成i; -
对于deduction任务,需要生成p和i,但不生成o。 -
对于induction任务,需要生成一组输入输出对(i,o),但不生成p。
另外对于induction任务,Proposer还会从历史的abduction和deduction任务中采样一个程序p,然后生成与之匹配的N个输入输出对(i,o),以及一段自然语言描述。
这种做法可以为induction任务提供更丰富的上下文信息,帮助Solver更好地理解和求解任务。
在生成过程中,Proposer会尝试控制新任务的难度和新颖度,以确保生成的任务对于当前的Solver来说既有意义又具备挑战性。
具体来说,“绝对零”引入了一个“可学习性”(learnability)的概念,用于估计一个任务对于当前的Solver模型来说有多大的学习价值。
它的计算方法是让Solver试着解决这个任务并统计其成功的概率。如果任务太简单或太难,那么这个任务的可学习性就会很低。Proposer的目标就是生成可学习性适中的任务。

生成出的新任务将被送到一个独立的代码执行器中进行验证,执行器会实际运行Proposer生成的程序,检查其是否满足以下条件:
-
语法正确性:程序能够在Python解释器中正常执行,没有语法错误; -
安全性:程序没有使用任何不安全的操作或库,如文件读写、系统调用等; -
确定性:程序在相同的输入下,总是产生相同的输出,没有随机性或不确定性。
通过这三个条件的检查,执行器可以滤除绝大部分无效或有害的任务。
对于通过验证的任务,执行器还会计算“可学习性奖励”,作为对Proposer行为的反馈。
最后,所有通过验证的任务会被存入一个任务buffer池中,供后续的训练使用。
在筛选完推理任务后,“绝对零”会转换为Solver的角色,开始解决这些任务,具体方式同样会根据任务的类型而有所不同:
-
对于abduction任务,Solver要根据给定的p和o推断可能的i。这个过程类似于“反向执行”程序; -
对于deduction任务,Solver要根据给定的p和i推断出o。Solver需要模拟程序的执行过程,得出最终的输出结果; -
对于induction任务,Solver要根据输入输出对(i,o),推断可能的程序p。Solver需要从有限的样本中总结出一般性的规律。
在求解任务的过程中,Solver可以利用语言模型已有的知识(如常见的算法模式、编程惯例等)来辅助任务的求解。
Solver生成的解会再次通过代码执行器进行验证。执行器会检查Solver给出的输入、输出或程序是否真的满足任务的要求。
如果满足,则视为Solver成功解决了任务,并给予相应的奖励;否则视为Solver失败,不给予奖励或给予惩罚。
这个奖励信号会作为Solver行为的反馈,帮助Solver学习如何更好地解决各种类型的推理任务。
同时,Solver的解决方案也会被记录下来,作为未来生成和求解类似任务的参考。
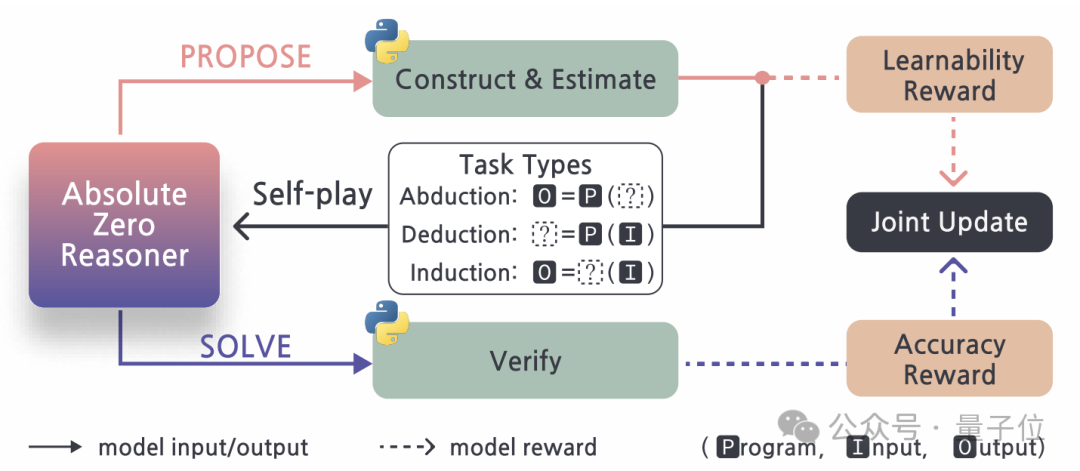
在每一轮迭代结束时,“绝对零”都会使用Proposer和Solver收集到的反馈信号,对整个模型进行联合优化和更新,使得Proposer生成的任务更有利于学习,Solver解决任务的能力也越来越强。
经过多轮迭代,“绝对零”最终可以收敛到一个很好的均衡点,在这个点上,Proposer生成的任务恰好匹配Solver的能力,Solver又能够从这些任务中学到足够多的知识。
数学代码任务性能双提升
在编程任务上,研究者使用了HumanEval+、MBPP+和LCB三个数据集。
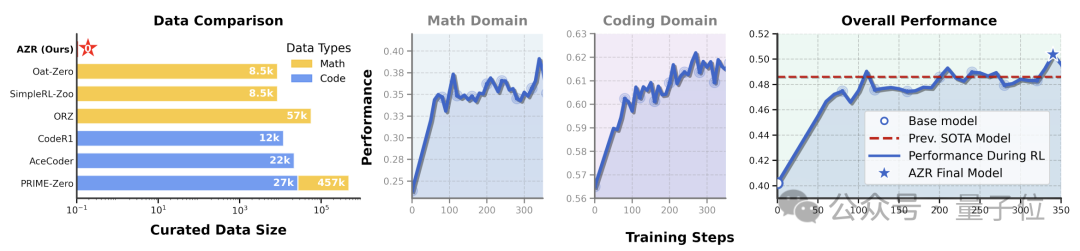
与未经“绝对零”训练的版本相比,“绝对零”将Qwen-2.5-7B-Coder的HumanEval+通过率从80.5%提高到了83.5%,将MBPP+的通过率从69.3%提高到了69.6%,将LCB的通过率从19.9%提高到了31.7%。
在数学推理任务上,研究者选取了6个具有代表性的数据集进行评测,包括AME’24、AME’25、AMC’23、MATH500、Minerva和Olypiad。
“绝对零”在这6个数据集上的平均准确率达到了39.1%,比未经“绝对零”训练的baseline高出了15.2个百分点。
其中,在MATH500数据集上,“绝对零”的准确率达到了72.6%,超出baseline 22.6个百分点;在AMC’23数据集上,“绝对零”的准确率为57.5%,超出baseline 17.5个百分点。
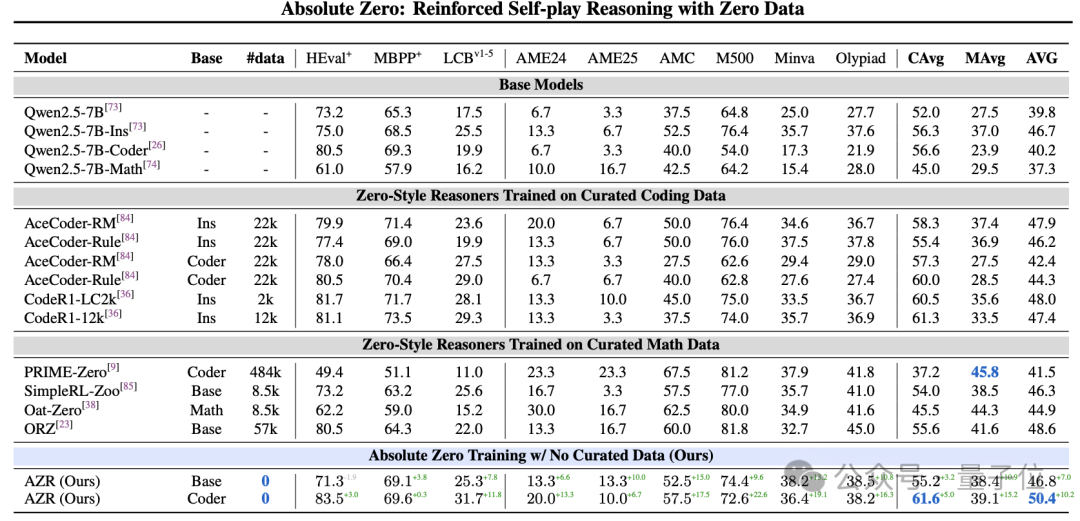
除了Qwen-2.5-7B-Coder,研究者还在其他几个预训练语言模型上测试了“绝对零”的性能:
-
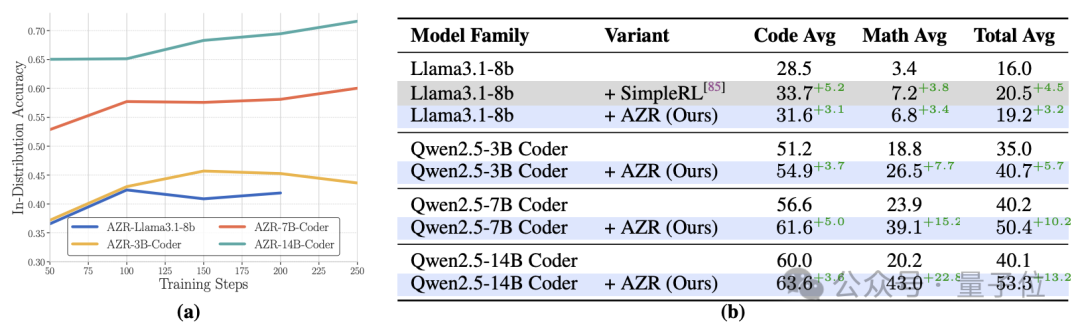
Qwen-2.5-3B-Coder:应用“绝对零”后编程任务平均通过率从51.2%提高到了54.9%,在数学任务上的平均准确率从18.8%提高到了26.5%; -
Qwen-2.5-14B-Coder:应用“绝对零”后,在编程任务上的平均通过率从60.0%提高到了63.6%,在数学任务上的平均准确率从20.2%提高到了43.0%; -
Llama-3.1-8B:应用“绝对零”后在编程任务上的平均通过率从28.5%提高到了31.6%,在数学任务上的平均准确率从3.4%提高到了6.8%。
通过对不同规模和类型的语言模型的测试,研究者还发现“绝对零”的性能提升与模型规模呈正相关——参数越多的模型,训练后的性能提升也越大。
例如在数学任务上,30亿参数的Qwen-2.5-3B-Coder模型提升了7.7个百分点,而140亿参数的Qwen-2.5-14B-Coder模型则提升了22.8个百分点。
这表明“绝对零”能够有效地利用大模型的能力,实现更高的推理性能提升。
论文地址:
https://arxiv.org/abs/2505.03335
(文:量子位)

