今天凌晨4点30,微软首席执行官SatyaNadella分享了,微软在量子计算的重大技术突破成果4D拓扑量子纠错码。
与2D相比,4D拓扑量子纠错码在编码效率、纠错能力、逻辑操作都非常出色,并且每个逻辑量子比特只需要极少的物理量子比特,可以一次性检查错误,并将错误率降低1000倍。
同时,这项全新的量子计算成果将应用在微软的Azure Quantum量子计算平台中,加速科研、医疗的研发效率
网友表示,这标志着一项重大进展,量子纠错长期以来一直是实现稳定、可扩展量子计算的主要瓶颈。
俺什么都不懂,但我相信你。
祝贺微软和Satya Nadella!这一成果展现了非凡的效率,彰显了在推进实用规模量子技术领域的领导地位。
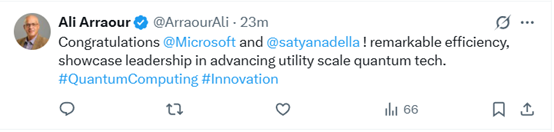
4D拓扑量子纠错码技术亮点
目前,多数量子计算机所使用的量子比特容易出错,无法独立完成可靠计算。要实现量子计算机解决复杂问题的潜力,需满足两个前提条件:一是使用高保真度的物理量子比特,二是应用能显著降低错误率以创建可靠逻辑量子比特的纠错码。
简单来说,物理量子比特像建房子的砖块,高保真度的是优质砖,才能搭稳房子。纠错码是施工图纸和质检员,既指导砖块正确堆砌,又随时检查修正歪斜、裂缝等问题,才能建造安全、高质量的房子。这样大家应该知道这个纠错能力的重要性了吧。
微软通过与多家硬件合作伙伴的协作,在量子纠错方面展现出先进能力,其量子比特虚拟化系统作为微软量子计算平台的核心组件,可利用高质量物理量子比特创建并纠缠出可靠的逻辑量子比特。
此前,微软团队将该系统应用于Atom Computing的中性原子,成功创建并纠缠了24个可靠的逻辑量子比特,还在计算过程中展示了检测和纠正错误以及处理量子比特丢失的能力;另一团队也创建了28个逻辑量子比特,能在执行可靠计算的同时检测和纠正错误。

由于如今的量子比特本质上存在噪声,所以通过量子纠错码将量子信息编码到更大的量子比特集合中,可使量子机器具备抗错能力。
在此基础之上,微软开发的新型4D拓扑量子纠错码适用于中性原子、离子阱和光子学等具有全连接特性的量子比特,能将物理量子比特的错误率降低多个数量级,以满足量子电路可靠运行的要求。
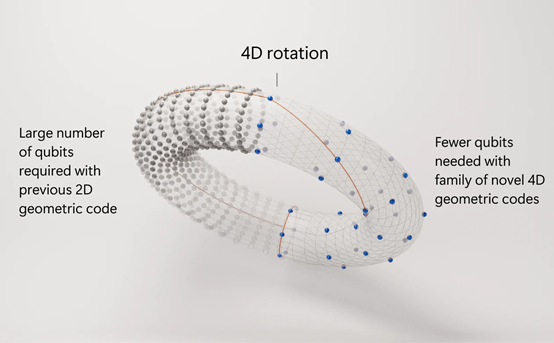
4D拓扑量子纠错码具有诸多优势:在构建每个逻辑量子比特时所需的物理量子比特数量极少,通过在4D空间中对码进行旋转,使构建逻辑量子比特所需的物理量子比特数量减少了5倍;
具备高效的逻辑操作,性能出色且具有单次测量特性,可快速纠正错误;能显著提升量子硬件性能,若将物理错误率从10⁻³降至约10⁻⁶,错误率可降低1000倍。

并且该系列码配备了一套完整的高效操作,可实现任何量子算法的编译,将其融入微软的全栈技术中,有望在短期内创建和纠缠50个逻辑量子比特,未来更有扩展到数千个逻辑量子比特的潜力。
4D拓扑量子纠错码架构简单介绍
4D拓扑量子纠错码的核心思想是利用4D空间的独特几何结构来增强量子纠错码的性能。在传统的二维拓扑量子纠错码中,量子比特被排列在一个二维平面上,而4D拓扑量子纠错码则将量子比特扩展到一个4D的超立方体结构中。这种高维的几何布局不仅为量子比特提供了更多的连接方式,还通过拓扑保护机制显著提高了量子信息的抗噪声能力。
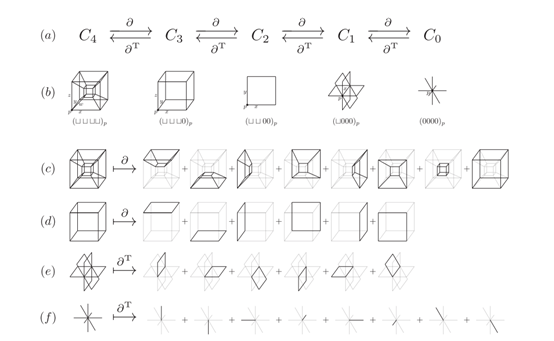
在4D空间中,量子比特被放置在超立方体的各个面上,而稳定化子则定义在超立方体的边和立方体上。这种布局方式使得量子纠错码能够利用4D空间的冗余性来检测和纠正错误。
4D超立方体的每个面都对应一个量子比特,而边和立方体则分别用于定义X型和Z型稳定化子。这种几何结构不仅为量子比特提供了更多的保护层,还使得错误能够在单次测量中被检测和纠正,从而实现了单次测量纠错的特性。
单次测量纠错是4D拓扑量子纠错码的一项重要特性,它允许在单次测量过程中完成错误检测和纠正。这一特性对于减少量子计算中的错误累积和提高计算效率具有重要意义。
在传统的量子纠错码中,错误检测通常需要多次测量,这不仅增加了计算的复杂性,还可能导致错误的进一步累积。
而4D拓扑量子纠错码通过其独特的几何结构和拓扑保护机制,能够在单次测量中完成错误的检测和纠正,大大提高了纠错效率。
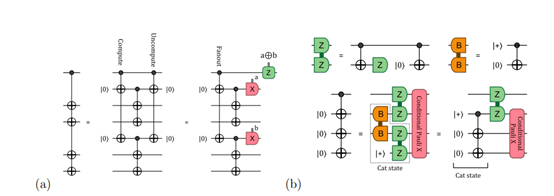
单次测量纠错的实现基于4D超立方体的边界冗余。在4D超立方体中,每个顶点和超立方体都提供了额外的冗余信息,这些信息可以用来检测和纠正错误。
通过测量超立方体的边和立方体上的稳定化子,可以快速确定是否存在错误以及错误的位置。一旦检测到错误,纠错算法可以立即采取措施纠正错误,从而避免了多次测量带来的复杂性和潜在的错误累积。
4D拓扑量子纠错码的几何结构和稳定化子的设计是其实现高效纠错和逻辑操作的关键。在4D超立方体中,量子比特被放置在各个面上,而稳定化子则定义在边和立方体上。这种布局方式不仅为量子比特提供了更多的保护层,还使得错误能够在单次测量中被检测和纠正。
稳定化子的设计是4D拓扑量子纠错码的核心。稳定化子是一组与量子纠错码的码空间对易的算符,它们的测量结果可以用来检测错误。
在4D拓扑量子纠错码中,稳定化子被设计为权重为6的算符,这意味着每个稳定化子涉及6个量子比特。这种高权重的稳定化子设计使得量子纠错码能够检测和纠正更多的错误类型,从而提高了纠错能力。
此外,4D拓扑量子纠错码还通过几何结构的变化来进一步优化性能。例如,通过旋转标准的4D晶格,可以减少所需的物理量子比特数量,同时保持码距不变。这种几何增强技术不仅提高了编码效率,还为实现单次测量纠错提供了可能。
4D拓扑量子纠错码比2D好在哪
从编码效率来看,2D拓扑量子纠错码通常需要大量的物理量子比特来编码少量的逻辑量子比特。例如,对于一个码距为d的2D表面码,需要d2个物理量子比特来编码2个逻辑量子比特。这意味着随着码距的增加,所需的物理量子比特数量呈平方级增长,极大地限制了量子计算的可扩展性。
相比之下,4D拓扑量子纠错码通过利用4D空间的几何特性,能够在相同的逻辑比特数量下显著减少所需的物理量子比特数量。
以4D环面码为例,其编码率为6d²个物理量子比特编码6个逻辑量子比特,且在某些优化的晶格结构下,还可以进一步减少物理量子比特的需求。这种高效的编码方式使得4D拓扑量子纠错码在资源利用上更具优势,尤其是在物理量子比特数量有限的近期内量子硬件中,能够实现更多的逻辑量子比特,从而提升量子计算的能力。
在纠错能力方面,2D拓扑码虽然具有较高的容错阈值,但它们通常需要多次测量来检测和纠正错误,这不仅增加了纠错的复杂性,还可能导致错误的进一步累积。
而4D拓扑量子纠错码由于其独特的几何结构,具备单次测量纠错的特性。这意味着在单次测量过程中,就可以完成错误的检测和纠正,大大提高了纠错的效率和可靠性。4D拓扑量子纠错码在面对复杂的错误模式时,也展现出了更强的纠错能力。
此外,从资源需求的角度来看,4D拓扑量子纠错码在实现相同纠错能力和逻辑操作功能的情况下,所需的物理量子比特数量显著减少。这对于当前和近期的量子硬件来说是一个巨大的优势,因为目前的量子硬件平台在物理量子比特的数量和质量上仍然存在限制。
通过减少物理量子比特的需求,4D拓扑量子纠错码不仅能够降低量子计算系统的硬件成本,还能够提高系统的可靠性和稳定性。此外,4D拓扑量子纠错码在实现逻辑操作时所需的辅助资源也相对较少,这进一步降低了量子计算的资源开销,使得量子计算在实际应用中更具可行性。
(文:AIGC开放社区)

