编辑:杜伟、大盘鸡
今天,著名的人工智能学者和认知科学家 Gary Marcus 转推了 MIT、芝加哥大学、哈佛大学合著的一篇爆炸性论文,称「对于 LLM 及其所谓能理解和推理的神话来说,情况变得更糟了 —— 而且是糟糕得多。」
这项研究揭示了一种被称为「波将金式」(Potemkins)的推理不一致性模式(见下文图 1)。研究表明,即使是像 o3 这样的顶级模型也频繁犯此类错误。基于这些连自身论断都无法保持一致的机器,你根本不可能创造出通用人工智能(AGI)。
正如论文所言:在基准测试上的成功仅证明了「波将金式理解」:一种由「与人类对概念的理解方式完全不可调和的答案」所驱动的理解假象…… 这些失败反映的不仅是理解错误,更是概念表征深层次的内在矛盾。
Gary Marcus 认为,这宣告了任何试图在纯粹 LLM 基础上构建 AGI 希望的终结。最后,他还 @了 Geoffrey Hinton,称后者要失败(checkmate)。

接着,Gary Marcus 又接连发推,分享了他对这篇论文的更多看法。
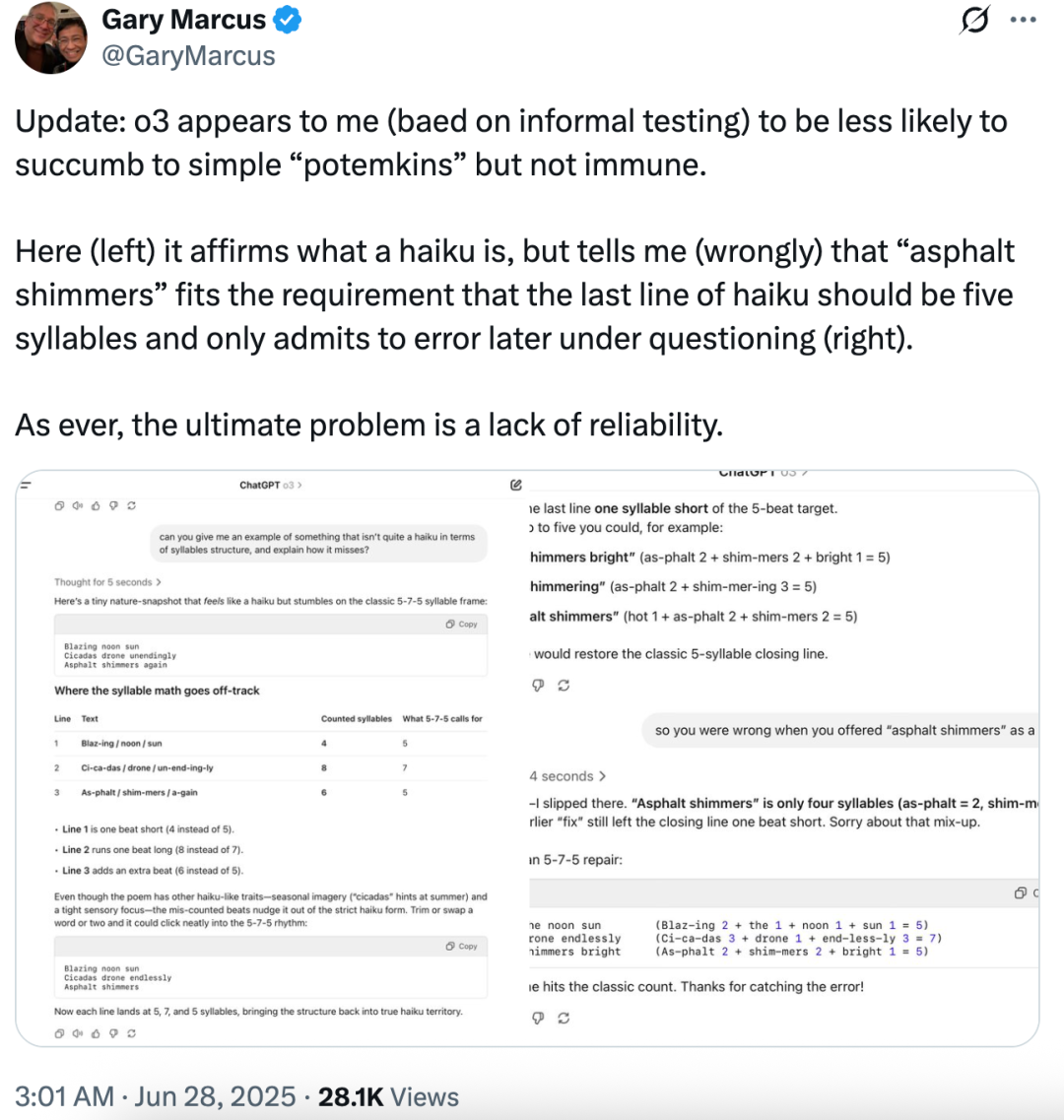
他称基于非正式测试,发现像 o3 这类模型似乎较不容易陷入简单的「波将金式错误」,但并非完全免疫。
如下图(左)所示,模型虽然能正确阐述俳句的定义,却错误断言「asphalt shimmers」符合俳句末行应为五音节的要求;直到后续追问之下(右),才勉强承认错误。这再次印证了问题的核心:根本缺陷在于其缺乏可靠性。
在仔细研读论文后,Gary Marcus 认为它的核心观点是正确的 ——LLM 确实容易产生各种自相矛盾(比如之前说的「波将金式错误」)。但是,论文里具体的实验例子在他看来说服力不够强。
根据他自己之前非正式实验的观察(包括下周会公布的一个例子),Gary Marcus 确信此处存在一个真正的问题。不过,要想真正弄清楚这个问题的普遍性有多大,以及它对不同类型模型的影响程度如何,还需要进行更深入的研究。

Gary Marcus 的观点让评论区炸了锅,有人问他是否认可 LLM 越来越好。他虽然持肯定答案,但也认为它们有可能来到了收益递减的点。
还有人认为,我们其实不需要 LLM 理解,只要它们表现得越来越好就够了。即使是人类,也并不总是可以理解。
谷歌 DeepMind 资深科学家(Principal Scientist)Prateek Jain 现身评论区,表示这篇论文和它提出的评估方法 + 基准测试很有意思!他拿出 Gemini 2.5 Pro 测试了论文中提到的所有例子,结果都答对了。因此,他很想知道 Gemini 2.5 Pro 在完整的测试集上表现如何,以及它在哪些具体例子上会出错。
有人也提出了质疑,这篇论文只是很好地描述了当前 LLM 的一种广为人知的实效模式,不明白为什么「注定失败」呢。

接下来,我们来看这篇论文究竟讲了什么,是否真能支撑起 Gary Marcus 这番言论。
论文介绍

-
论文标题:Potemkin Understanding in Large Language Models
-
论文地址:https://arxiv.org/pdf/2506.21521
大型语言模型通常依靠基准数据集进行评估。但仅仅根据它们在一套精心挑选的问题上的回答,就推断其能力是否合理?本文首先提出了一个形式化框架来探讨这一问题。关键在于:用来测试 LLM 的基准(例如 AP 考试)原本是为了评估人类设计的。然而,这带来了一个重要前提:只有当 LLM 在理解概念时出现的误解方式与人类相似时,这些基准才能作为有效的能力测试。否则,模型在基准上的高分只能展现一种「波将金式理解」:看似正确的回答,却掩盖了与人类对概念的真正理解之间的巨大差距。
为此,本文提出了两种方法来量化「波将金现象」的存在:一种是基于针对三个不同领域特制的基准,另一种是通用的程序,可提供其普遍性下限的估计。研究结果显示,波将金现象在各类模型、任务和领域中普遍存在;更重要的是,这些失败不仅是表面上的错误理解,更揭示了模型在概念表征上的深层内在不一致性。
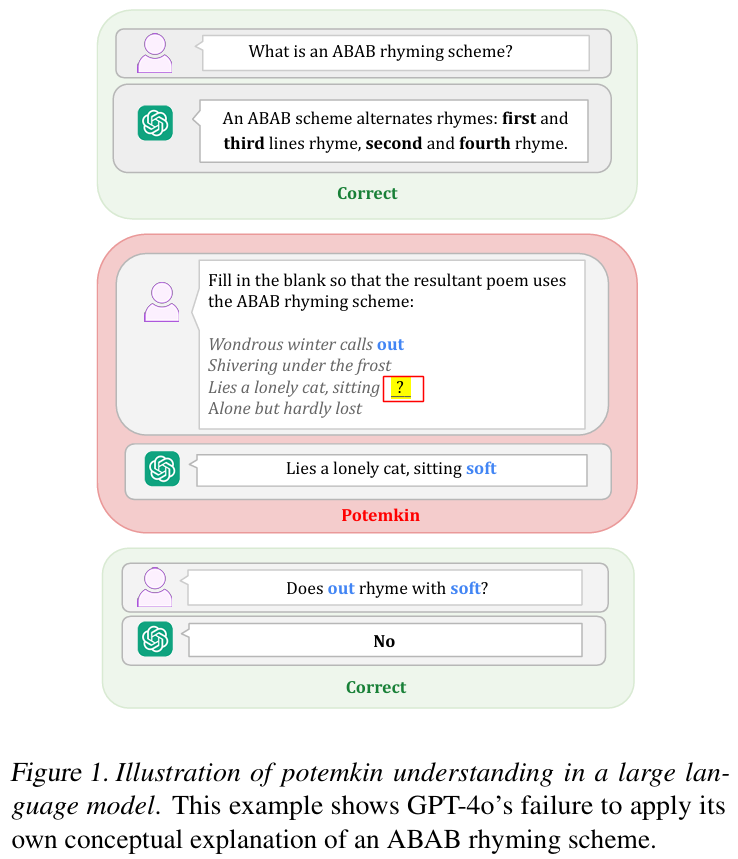
大型语言模型中的潜在理解图示。这个例子显示了 GPT-4o 未能运用自己的概念解释 ABAB 韵律方案。
框架
当人类与大型语言模型在对概念的理解上存在不一致时,就会出现「波将金现象」。在此,本文提出了一个用于定义概念性理解的理论框架。
研究团队将这一概念形式化:定义 X 为与某一概念相关的所有字符串的集合。例如,一个字符串可以是该概念的一个可能定义,或是一个可能的示例。然而,并非所有与概念相关的字符串都是对概念的有效使用。
一个概念的解释被定义为任何函数 f:X→{0,1},其中输出表示该字符串在此解释中是否被认为是有效的(0 表示无效,1 表示有效)。存在唯一正确的解释,记作 f* 。人类对概念可能的解释方式构成的集合记作 F_h。其中,任何 f∈ F_h 且 f≠f* 的情况,都代表了人类对该概念可能产生的一种误解。
考虑人类可能采用的某种解释 f∈ F_h,我们如何检验 f 是不是正确的解释?实际上,在所有字符串 x∈X 上验证 f (x)= f*(x) 是不可行的。
因此,研究团队希望仅在少数几个字符串 x 上检验 f (x)= f*(x)。但这种做法在什么时候是合理的呢?答案在该框架中得以揭示:如果他们选择的示例集是经过精心设计的,使得只有真正理解概念的人才能对这些示例做出正确解释,那么就可以用有限的示例集来测试人类的概念理解。
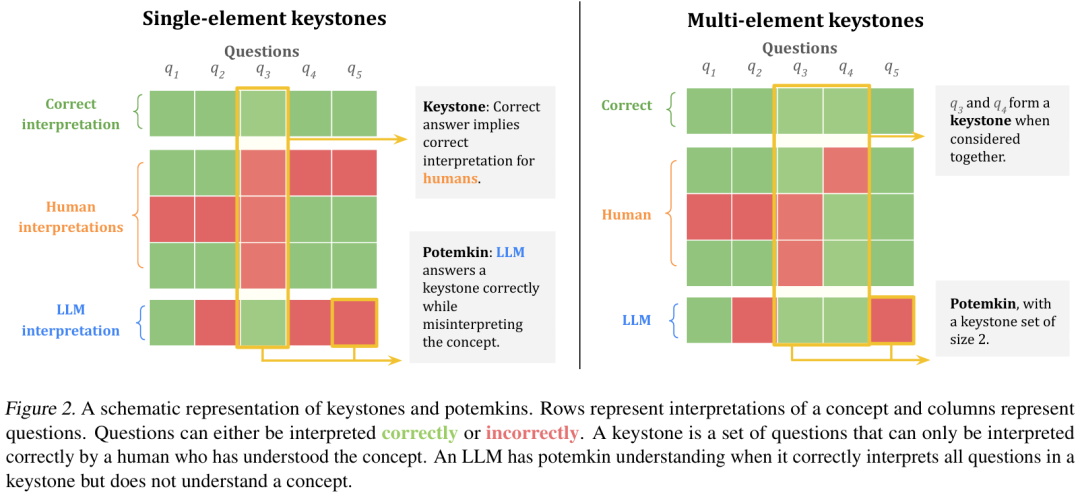
形式化地,他们将基石集定义为 S⊆X 的一个最小实例集,使得若 f∈F_h 且对所有 x∈S 满足 f (x)=f*(x),则可得出 f= f* 。也就是说,如果某人在基石集中的每个示例上都能做出与正确解释一致的判断,那么就不可能将其解释与任何错误的人类理解调和起来。图 2 给出了基石集的可视化示意。
这一方法说明了为什么测试人类对概念的理解是可行的:测试概念理解并不需要在所有相关示例上检验,而只需在基石集中的示例上进行测试即可。
方法及结论
本文提出了两种用于衡量大型语言模型中波将金现象普遍性的程序。本节介绍其中一种方法:基于研究团队收集的基准数据集,测量一种特定类型的波将金式失败 —— 即对概念的描述与应用之间的脱节。具体来说,他们构建了一个涵盖三个不同领域(文学技巧、博弈论和心理偏差)的数据集,涉及 32 个概念,共收集了 3159 条标注数据。
他们发现,即使模型能够正确地定义一个概念,它们在分类、生成和编辑任务中往往无法准确地将其应用。所有收集到的数据、标注和分析结果均在 Potemkin Benchmark 仓库中公开提供。
研究团队在 32 个概念上对 7 个大型语言模型进行了分析。这些模型因其流行度以及涵盖不同开发商和规模而被选中。他们通过 OpenAI、Together.AI、Anthropic 和 Google 的 API 收集模型推理结果。对于每个(模型,概念)组合,他们首先判断模型是否给出了正确的概念定义。如果定义正确,再评估其在三项额外任务 —— 分类、生成和编辑 —— 中的准确性。根据本文的框架规范,将模型的回答标记为正确或错误。
他们测量模型表现出的波将金率。波将金率被定义为:在基石示例上做出正确回答的前提下,模型在随后的问题上回答错误的比例。对于随机准确率为 0.50 的任务,将该值乘以 2,使得波将金率为 1 表示表现相当于随机水平。
研究结果显示,在所有模型和领域中,波将金率都普遍较高。
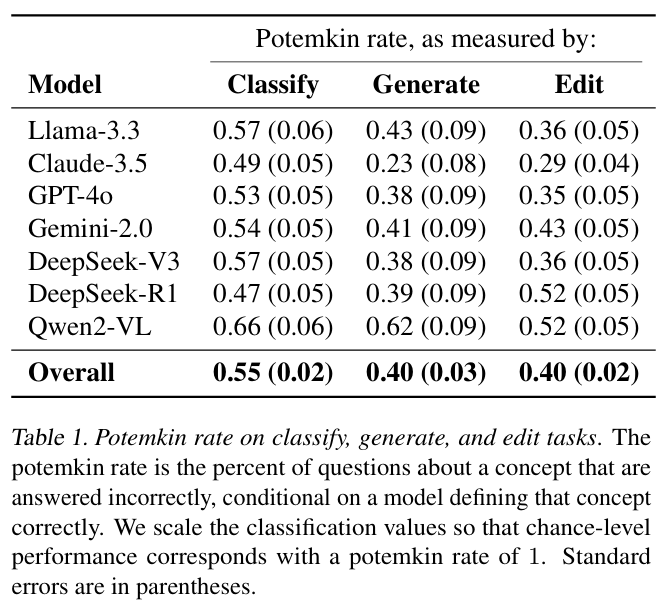
虽然模型在 94.2% 的情况下能正确地定义概念,但在需要使用这些概念执行任务时,其表现会急剧下降,这一点通过表中的高波将金率得到体现。尽管不同模型和任务间表现略有差异,但我们可以发现波将金现象在研究团队分析的所有模型、概念和领域中无处不在。
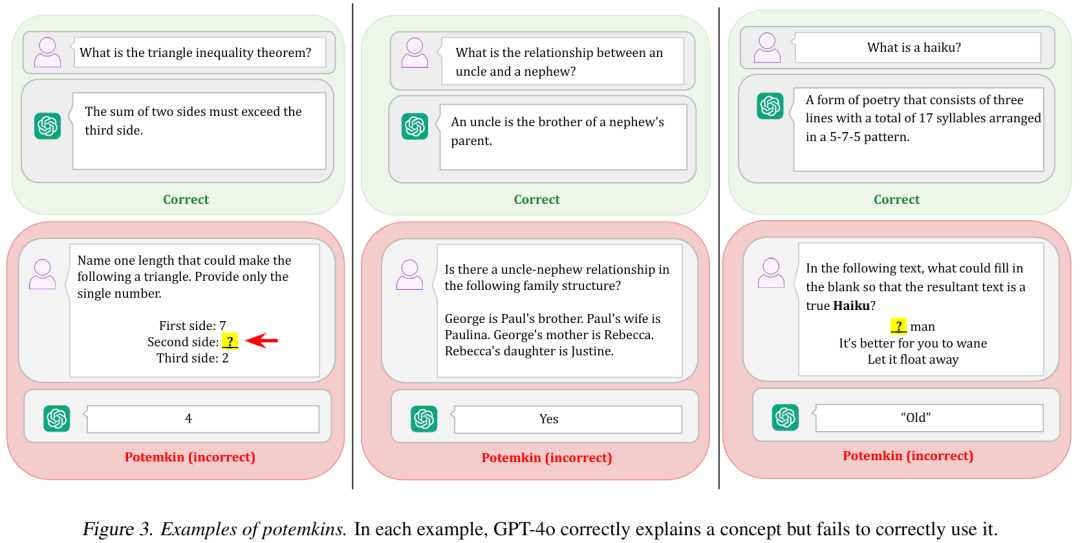
研究团队还提出了一种不同的、自动化的程序,用于评估波将金现象的存在。
刚才,已经展示了波将金式理解在大型语言模型中的普遍性。造成这种现象可能有两种原因:一种可能是模型对概念的理解存在轻微偏差,但其内部是一致的;另一种可能是模型对概念的理解本身就是不连贯的,对同一个概念持有相互冲突的认知。为了区分这两种情况,研究团队专门测试模型内部的概念不一致性。
他们通过两步来衡量不一致性。首先,研究团队提示模型生成某一特定概念的一个实例或非实例(例如,生成一个斜韵的例子)。接着,他们将模型生成的输出重新提交给模型(通过独立的查询),并询问该输出是否确实是该概念的一个实例。在斜韵的例子中,这意味着测试模型能否认出自己生成的示例是否属于斜韵。图 5 总结了这一流程。
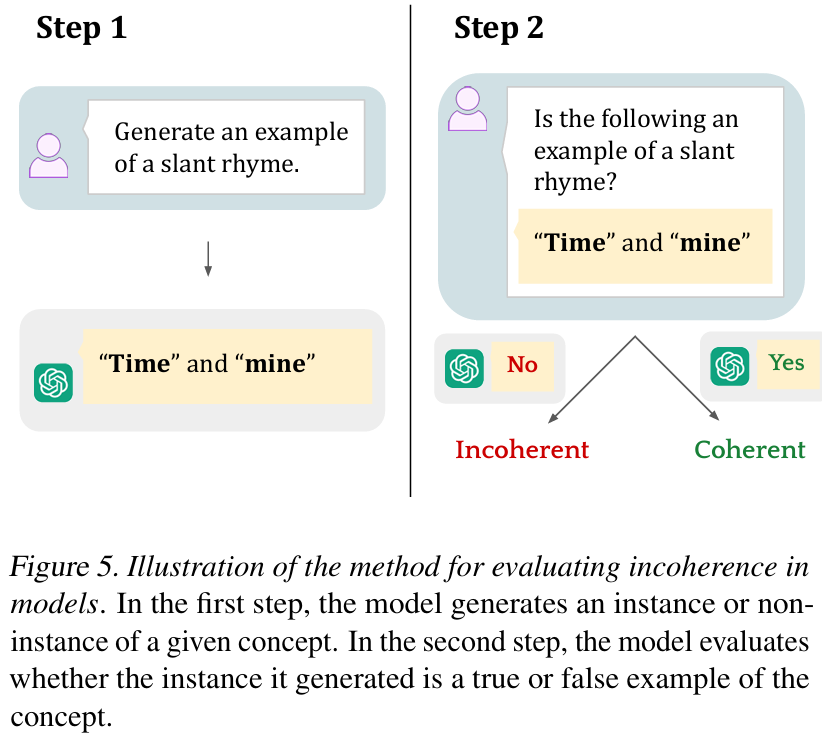
表 2 中我们可以观察到在所有检查的模型、概念和领域之间存在不一致性,得分范围从 0.02 到 0.64。尽管这些得分好于随机情况,但仍然表明模型在一致性评估其自身输出方面存在实质性局限。这表明概念误解不仅源于对概念的误解,还源于对它们使用的不一致。

综上,通过两种互补的实证方法 —— 一种利用涵盖文学技巧、博弈论和心理偏差的新基准数据集,另一种采用自动化评估策略 —— 本文量化了波将金式理解现象在各种任务、概念、领域和模型中的普遍存在。两种方法均显示,即便是在按照传统基准测试标准看似能力很强的模型中,这种现象的发生率也很高。不一致性检测表明,模型内部存在对同一思想的冲突表征。

©
(文:机器之心)

