研究方向 | 大语言模型与推荐系统
近年来,类似于 OpenAI 的 o1 等慢思考(slow-thinking)推理系统在解决复杂推理任务方面展现了卓越的能力。这些系统在回答查询之前,经过较长时间的思考与推理,能够生成更加全面、准确且有理有据的解决方案。
然而,这些系统主要由工业界开发和维护,其核心技术尚未公开披露。因此,越来越多的研究工作开始致力于探索这些强大推理系统背后的技术基础。在此背景下,我们的团队致力于实现类似于 o1 的推理系统,希望开发一个技术开放的慢思考推理模型。
本文介绍了我们在复现 o1 类推理系统方面的研究进展,提出了一个“模仿、探索和自我提升”的框架,作为训练推理模型的主要技术手段。在本工作中,我们仅使用 1100 条蒸馏的长思维链数据作为种子数据,通过自我探索与改进就能够取得不错的效果: 在非常困难的数学奥林匹克数据集 AIME 达到了 46.7 的评分,在 MATH-OAI 上也达到了 87.4 的评分,在跨学科 GPQA 上也取得了 53.0 的评分。
 Imitate, Explore, and Self-Improve: A Reproduction Report on Slow-thinking Reasoning Systems
Imitate, Explore, and Self-Improve: A Reproduction Report on Slow-thinking Reasoning Systems
论文链接:
https://arxiv.org/pdf/2412.09413
项目链接:
https://github.com/RUCAIBox/Slow_Thinking_with_LLMs

背景
慢思考推理系统通过在回答用户查询之前进行深入的内部推理,能够有效解决复杂的推理任务。这种方法不同于传统的链式思维(chain-of-thought)推理,它允许模型在更长的时间内进行深度思考,并利用更多的计算资源来推演,从而生成更为复杂和细致的推理步骤。此类能力在解决数学问题、编程挑战和逻辑推理等任务中尤为突出。
然而,由于工业界对这些系统的核心技术细节通常保密,学术界在再现这些系统时面临着诸多挑战。现有的研究大多局限于特定领域(如数学领域),或基于相对较弱的基础模型,导致所实现的系统在性能上与工业级系统相比存在明显差距。因此,开发一个技术开放的 o1 类推理系统,仍然是一项极具挑战性的任务。

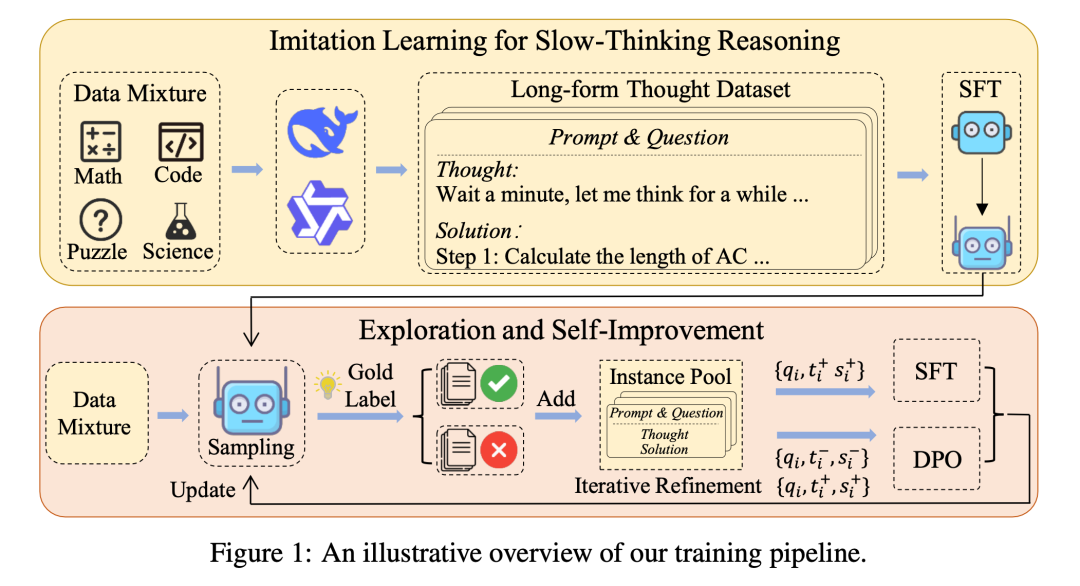
为了实现这一目标,我们提出了一个“模仿、探索与自我提升”的三阶段训练框架。该框架旨在通过训练模型模仿长思维链中的思考模式,鼓励模型在面对具有挑战性的问题时进行深入探索,并通过迭代改进训练数据,不断提升模型的推理能力。
2.1 模仿(Imitate)
在初始阶段,我们通过收集和整理长思维链数据,对模型进行微调,使其能够在回答问题之前,生成详细的内部推理步骤。这些思维过程包括规划、分而治之、自我修正、总结和回溯等复杂的推理行为。
为了构建这样的训练数据,我们采用了数据蒸馏的方法,从现有的 o1 类推理系统(如 和 )中提取关于Math,Code,Science,Puzzle领域的长思维链。这些数据经过预处理后,作为模型的训练数据,帮助模型学习如何按照指定的格式生成长思维链和最终的解决方案。

仅仅通过模仿,模型可能还不足以处理具有挑战性的问题。为此,我们鼓励模型在困难的问题上进行探索,生成多个可能的解答路径(称为“轨迹”)。通过生成多样化的解答,模型有更大的机会找到正确的解决方案。
在实践中,我们采用了简单的搜索策略,对每个问题生成多个解答轨迹,直到找到包含正确答案的解答。随着生成的轨迹数量增加,我们可以收集到更多高质量的解答,这些解答也有助于进一步提升模型的能力。
最后,我们利用模型在探索过程中获得的正确轨迹,进一步强化其推理能力。通过不断将新的高质量解答融入训练数据,模型能够在每次迭代中改进自身,特别是在处理复杂任务时,表现出更为卓越的推理能力。
在这个阶段,我们采用了两种优化方法来进一步提升模型的推理能力。一是继续进行监督微调(SFT),利用模型生成的高质量解答作为训练数据,帮助模型不断优化其生成能力;二是采用直接偏好优化(DPO),通过比较高质量与低质量解答之间的差异,指导模型学习更加优越的生成策略,从而提高其解答质量和推理效果。

3.1 实验设置
为了验证我们方法的有效性,我们在三个具有挑战性的基准数据集上进行了广泛的实验:
1. MATH-OAI:包含500道数学竞赛题目,来源于 MATH 测试集。
2. AIME:由30道难度较高的数学问题组成,专为挑战顶尖高中生的解决问题能力而设计。
3. GPQA:包含198道生物、物理和化学领域的选择题。
由于 在多个评测中表现优异,能够提供出色的推理能力,我们选择了该模型作为基础模型。为了与工业级系统进行全面比较,我们将我们的模型与几款领先的 o1 类模型进行了对比,包括 、 和 。
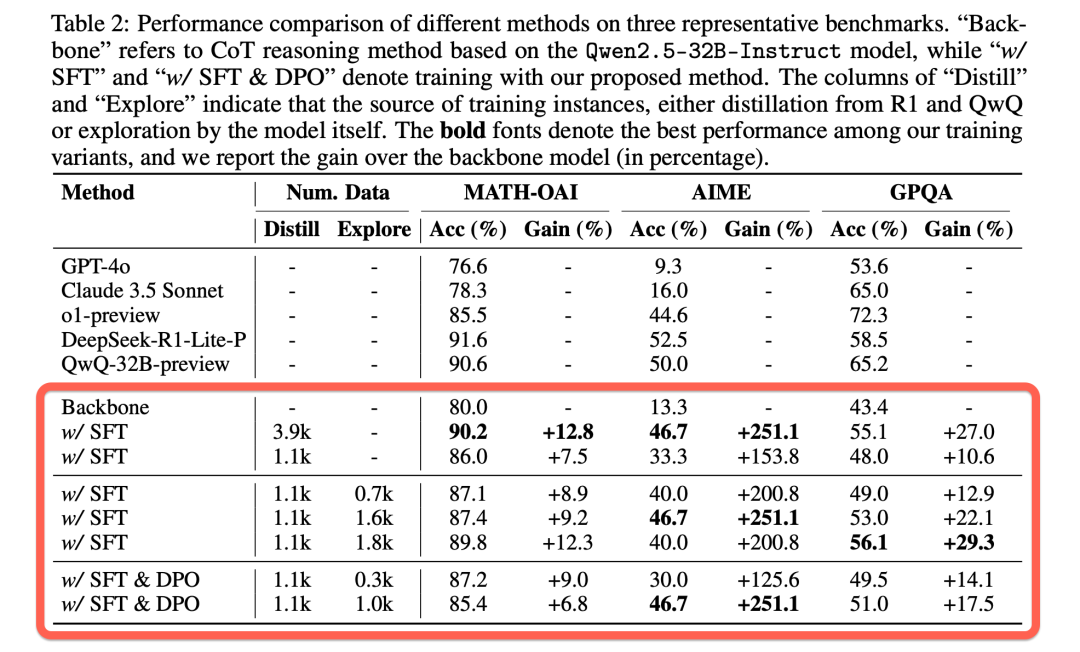 工业界慢思考推理系统在三个基准测试中都取得了优异的表现,尤其在最具挑战性的基准测试 AIME 上改进显著。总体而言,o1-preview 表现出更均衡的性能,而 和 在数学领域表现更好。这些结果表明慢思考在增强 LLM 的复杂推理能力方面的有效性。
使用经过预处理后从 和 获得的 3.9k 个蒸馏实例进行SFT后,我们的方法在 AIME 上实现了 46.7% 的准确率,在 MATH-OAI 上实现了 90.2% 的准确率(表2第二部分的第一组)。同时,训练数据从 1.1k 增加到 3.9k 带来的效果表明,增加高质量数据的数量可以有效提高模型性能(表2第二部分的第一组)。
我们方法的迭代训练变体(表2第二部分中的第二组和第三组)也可以在三个基准上取得令人满意的结果。使用带有 SFT 1.1k 的变体作为参考,我们观察到结合探索和自我改进可以有效提高性能,例如,MATH-OAI 的性能从 86.0% 提高到 89.8%,AIME 的性能从 33.3% 提高到 46.7%。
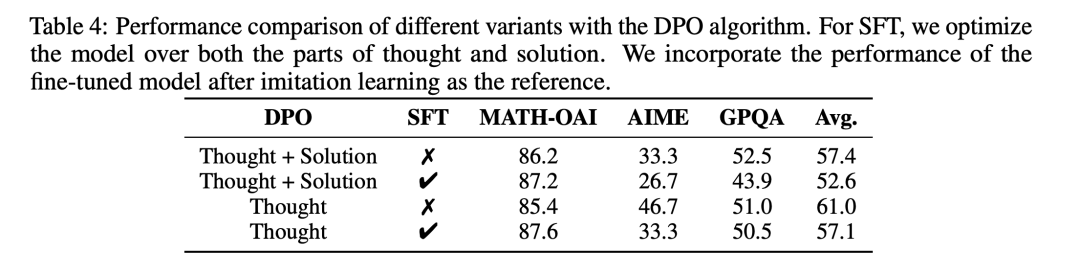
去除困难数学问题会显著降低模型的表现,特别是在 AIME 这一最具挑战性的基准上。这表明困难问题对于提升推理模型的能力至关重要,尤其是在需要较长思考过程的情况下。
仅使用数学数据(不包含其他领域数据)有助于提升 AIME 的性能,但对 MATH-OAI 和 GPQA 的性能有负面影响。
工业界慢思考推理系统在三个基准测试中都取得了优异的表现,尤其在最具挑战性的基准测试 AIME 上改进显著。总体而言,o1-preview 表现出更均衡的性能,而 和 在数学领域表现更好。这些结果表明慢思考在增强 LLM 的复杂推理能力方面的有效性。
使用经过预处理后从 和 获得的 3.9k 个蒸馏实例进行SFT后,我们的方法在 AIME 上实现了 46.7% 的准确率,在 MATH-OAI 上实现了 90.2% 的准确率(表2第二部分的第一组)。同时,训练数据从 1.1k 增加到 3.9k 带来的效果表明,增加高质量数据的数量可以有效提高模型性能(表2第二部分的第一组)。
我们方法的迭代训练变体(表2第二部分中的第二组和第三组)也可以在三个基准上取得令人满意的结果。使用带有 SFT 1.1k 的变体作为参考,我们观察到结合探索和自我改进可以有效提高性能,例如,MATH-OAI 的性能从 86.0% 提高到 89.8%,AIME 的性能从 33.3% 提高到 46.7%。
去除困难数学问题会显著降低模型的表现,特别是在 AIME 这一最具挑战性的基准上。这表明困难问题对于提升推理模型的能力至关重要,尤其是在需要较长思考过程的情况下。
仅使用数学数据(不包含其他领域数据)有助于提升 AIME 的性能,但对 MATH-OAI 和 GPQA 的性能有负面影响。
仅使用 Thought 的实验表现出较为积极的结果。可能的原因是思考过程是学习的核心部分,一旦思考过程得到很好的建立,LLM 能够容易地生成相应的解决方案。
当同时使用 Thought 和 Solution 时,SFT 损失对优化似乎没有正面影响,这可能是因为解决方案已经在 DPO 训练过程中得到了整合。

研究意义
4.1 核心贡献
我们提出了一个简单而有效的三阶段训练框架,通过“模仿、探索和自我提升”来训练模型,实现了类似 o1 的慢思考推理能力。
我们证明了长思维链在跨领域的可迁移性,即使只在数学领域进行训练,模型也能在科学和其他领域展示出色的推理能力。
我们给出了一个开放技术细节的类 o1 系统实现方法,在多个具有挑战性的基准数据集上取得了与工业级系统相当的性能。
4.2 研究意义
我们的研究表明,通过适当的训练策略和数据选择,大语言模型能够有效地生成长思维链,从而解决复杂的推理任务,这有助于推动开源社区的相关研究。
此外,我们的方法不依赖复杂的奖励模型或显式的树搜索算法,使得实现过程更加简单高效,这为未来在更多领域和更大规模上训练类似的推理系统提供了可行的途径。
扩展探索的规模:增加模型在探索阶段的规模,以更全面地提升模型能力。
丰富训练数据:通过引入更多领域和难度级别的高质量数据,进一步增强模型的泛化能力。

总结
本文介绍了我们在实现 o1 类慢思考推理系统方面的研究进展,提出了一个“模仿、探索和自我提升”的训练框架。通过实验验证,我们的方法在多个具有挑战性的基准数据集上取得了优异的性能,证明了其有效性和巨大潜力。我们的主要发现可以概括为以下几点:
通过使用少量高质量的演示数据,可以有效激发 LLM 进行慢思考的能力。一旦这种能力建立,它似乎能够自然地在不同领域之间泛化。
数学领域的演示数据尤其适合用于提升 LLM 的慢思考能力,且包含较长思考过程的数据在提升模型解决复杂问题的能力方面尤其有效。
与 LLM 在快速思考模式下生成的正式回复不同,慢思考过程通常以灵活、非正式的方式表达,帮助引导模型走向正确的解题路径。
慢思考能力可以通过探索和自我改进有效增强,而离线学习的方法带来的改进通常主要发生在初期迭代,尤其是在面对具有挑战性的任务时。
模型的慢思考示例
(文:PaperWeekly)