
极市导读
ARFlow是首个将自回归建模引入流模型,借助“因果有序噪声序列”与“chunk‑wise 混合线性注意力”,在ImageNet 128×128 上将 FID 从 14 降至约 4,既突破长程依赖瓶颈,又兼顾效率与生成质量。 >>加入极市CV技术交流群,走在计算机视觉的最前沿
本文目录
1 ARFlow:混合线性注意力的 Autoregressive Flow
(来自 UC Santa Cruz,MIT 等)
1.1 ARFlow 研究背景
1.2 Flow-based Model 和 Chunkwise 线性注意力简介
1.3 ARFlow 机制介绍
1.4 混合线性注意力
1.5 实验结果
太长不看版
结合了自回归建模方式的 Flow Model,搭配混合线性注意力机制。
本文把自回归建模与 Flow Model 结合到了一起。训练的时候,在每个 step,从一个语义类别中采样多个图像,添加不同程度的噪声,构建一个 causally-ordered 的序列。其中,噪声较强的图像在噪声较弱的图像之前。这个设计使得模型能够学习类别级别得变化,同时在 flow 过程中维持因果关系。生成的时候,模型从早期的 denoising step 中自回归地改变先前生成的图像,形成连贯的生成轨迹。此外,还设计了一种定制的混合线性注意机制,以提高计算效率。
1 ARFlow:混合线性注意力的 Autoregressive Flow
论文名称:ARFlow: Autoregressive Flow with Hybrid Linear Attention
论文地址:
https://arxiv.org/pdf/2501.16085
1.1 ARFlow 研究背景
与遵循曲线轨迹的 Diffusion Model 不同,Flow Model 通过直线路径连接数据和噪声分布,为生成建模提供了一种更直接的有效的方法。然而,目前 Flow-based 的方法的一个关键的问题是:很难捕获长期依赖关系。为什么会有这个问题呢?作者解释说是由于:在每个生成的步骤,只能访问到前序步骤损坏的图片,这就迫使模型把所有的历史信息压缩到单个噪声的中间状态。因此,这种约束可能会降低模型在整个生成过程中保持语义一致性以及结构连贯性的能力。也就是说,Flow Model 本质上受到它们的马尔可夫性质的限制:每个生成步骤只能访问来自直接上一步的信息,从而限制了它们保持远程一致性的能力。
与依赖马尔可夫假设的 Flow Model 相比,Autoregressive Model 通过 hidden state 自然地维护历史信息。在自回归建模中,每个 token 的预测明确地依赖于所有先前的 token。这种建模方式对于构建全局关系而言很有效果,哪怕是几百万个 token 组成的序列依然有效。那么,如果能够正确地将 Flow Model 和 Autoregressive Model 结合在一起,就会允许 Flow Model 直接优化生成轨迹之间的一致性,同时保持其计算量的优势。
1.2 Flow Model 和 Chunkwise 线性注意力简介
Flow Model
Flow Model 是一种利用连续时间随机过程,来做生成式建模的方法。Diffusion Model 遵循数据和噪声分布之间的曲线路径,Flow Model 与它不同,创建直线轨迹,来实现更高效的训练和采样。
Flow Model 通过精心设计的过程逐渐将标准高斯噪声 转换为图像 latent :

其中, 表示连续时间参数。调度函数 和 起着至关重要的作用:随着 的增加, 从 1 单调减小到 0 ,控制目标图像的贡献,而 从 0 增加到 1 ,逐渐引入噪声。常见的选择是线性调度,其中:

这在干净图像潜在噪声和纯噪声之间创建了一个平滑的插值,使得模型进行稳定的训练和生成。速度场中具有参数 的 Flow model 可以通过最小化下式来进行优化:
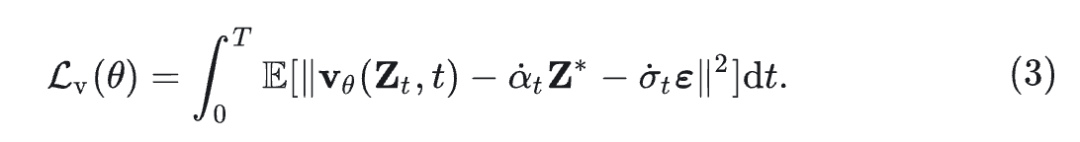
式中, 预测 的瞬时变化,目标确保该预测结果与 ground truth velocity 相匹配。这个目标确保了准确预测整个轨迹 latent representation 的瞬时变化,从而能够对生成过程进行精确控制。
Chunkwise 线性注意力
将 矩阵表示为 ,其中 是序列长度, 是头部维度,对于每个 head,线性注意力具有以下两个等效的循环和并行形式:
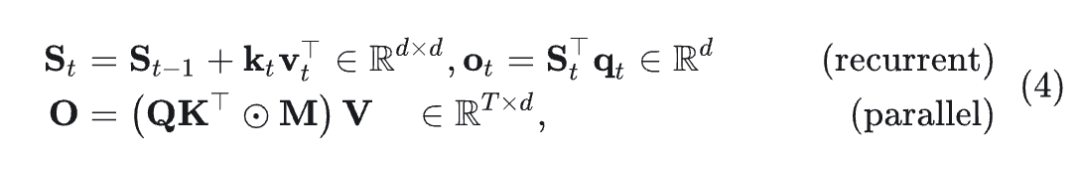
其中, 是 causal mask。另一个等效的 chunk-wise parallel form 在 parallel form 和 recurrent form 之间平衡,从而实现 subquadratic hardware-efficient training。
考虑一个输入序列 被分成不重叠的 chunk,其中 为单个 chunk的长度, 为 chunk 的数量。令 表示处理 个 chunk 之后的隐藏状态(即在时间步 之后)。
定义 作为第 个 chunk 的 Query 向量, 遵循类似的定义。那么 chunk-level recurrence 可以写成:
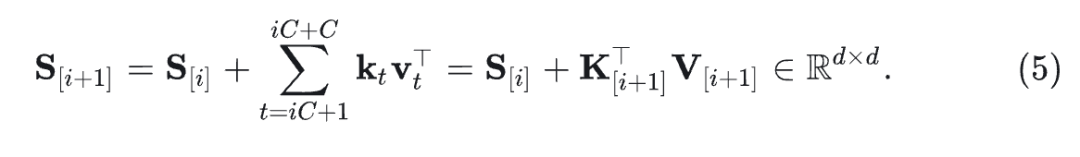
intra-chunk (parallel) 输出为:
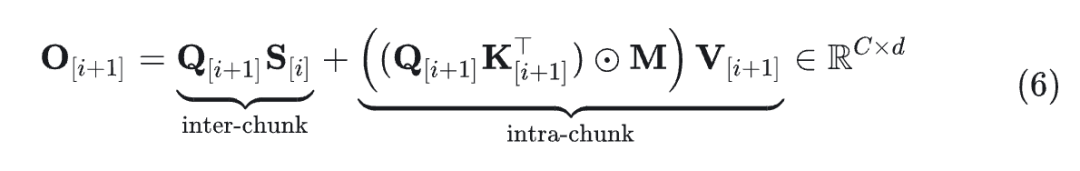
intra-chunk component \mathbf{O}^{\text{intra}}_{[i+1]} 需要的计算复杂度: O(C^2 d + C d^2) 。
inter-chunk component \mathbf{O}^{\text{inter}}_{[i+1]} 需要的计算复杂度: O( C d^2) 。
一旦 C 固定为一个小常数 (例如,实践中为 64 或 128),整体训练时间在序列长度 T 中是线性的。值得注意的是,输出计算是高度并行的,与循环形式相比,chunklevel recurrence 显著地减少了循环步骤,从而实现硬件高效的训练[1]。
1.3 ARFlow 机制介绍
ARFlow 把自回归集成到一个 Flow-based 架构中。
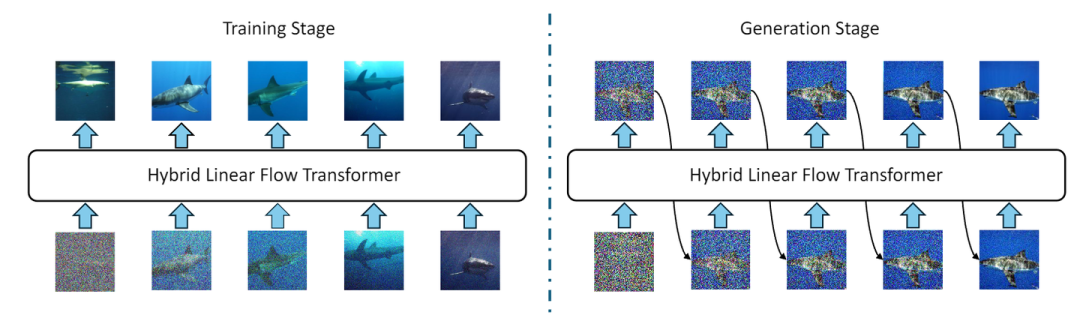
训练阶段: ARFlow 从同一语义类别中采样多个图像以形成序列。此外,与原始 Flow Model 不同,对这些采样图像应用了不同 level 的独立噪声,将它们排在一个序列中,其中更严重的损坏图像先于噪声较小的图像,以帮助在去噪过程中建立清晰的因果关系。
首先,从 condition 的相同语义类别中采样 个图像 ,以及 个独立采样的时间值 。这种采样策略确保了多样化的内容,同时保持每个序列中的语义一致性。
然后,通过 Encoder(式 1)将这些图像转换为 latent representation ,然后根据 Flow 过程施加独立采样的噪声 (式 2)。噪声样本的独立性进一步增强了学习信号的多样性。最后,根据 的时间顺序排列序列:
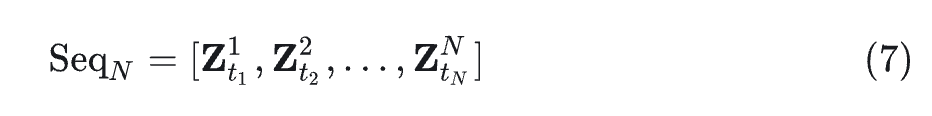
这种丰富的序列用来优化 Flow Model:
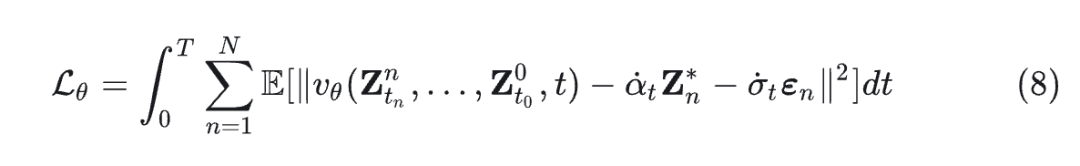
推理阶段: ARFlow 进行自回归操作:在每一步,模型以先前生成的图像的完整序列为 condition,同时遵循 Flow 来预测下一个图像。这种自回归的模式允许模型同时捕获到和局部的变化 (通过 Flow-based updates) 和长距离依赖 (通过过去状态的记忆),从而产生更连贯和更稳定的生成轨迹。
在生成阶段,每个自回归步骤对应于整个 latent 图像 Z 的一个完整的 Flow sampling step,而不是单个 token 。这种设计选择在保持自回归建模的好处的同时保持了效率。
1.4 混合线性注意力
此外,考虑到 ARFlow 被期待生成长序列图像 token,本文提出了一种混合线性注意力,确保该框架在计算上仍然可行且可扩展。
因为 ARFlow 中的自回归关系是在 image-level 而非 patch-level 建模的,本文提出了一种定制的混合线性注意机制:
-
把每张图片当作一个 chunk。 -
在 chunk 之内进行 full attention 来建模单个图像的生成,平行处理。 -
在 chunk 之间进行 causal attention 来建模 image-wise 的关系,顺序处理。
这种设计保留了 ARFlow 引入的必要因果关系,并实现了高效的并行处理。
具体来讲,为了得到一个序列,对每个 latent image ,将其分成 个 patch,得到 where ,其中,一般 ,当图像大小为 的时候。
然后,将其拼接成序列: 。与标准语言建模类似,应用 线性投影来获得 ,其中 。
但是在实践中, 可能非常大,这使得基于 Transformer 的自回归建模很昂贵,尤其是在由于 KV cache 大小较大而在推理过程中。为了解决这个问题,采用线性注意力来降低复杂性。
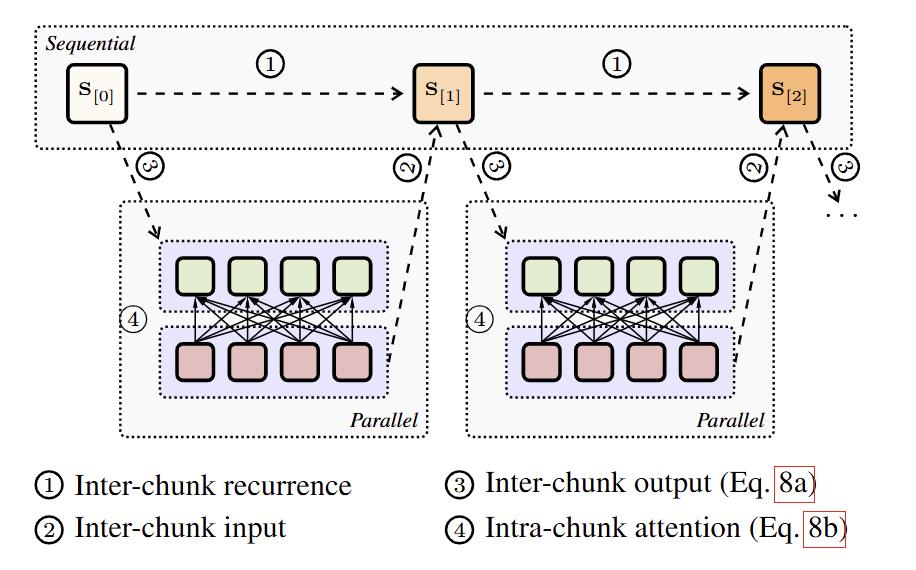
与语言建模不同,Flow Model 不需要在每个图像中强制 token (或者 patch) 之间的因果关系。相反,建模双向交互可以提高生成图像的连贯性和质量。为了利用这一点,ARFlow 使用混合线性注意机制,将序列划分为 chunk,每个 chunk 代表一个单独的图像,即 。
如图 2 所示,混合线性注意力通过 hidden states 保留顺序依赖关系,同时允许 chunk 内部的并行处理。与 next-token prediction 不同,Flow Model 专注于 next de-noising image prediction,支持 chunk 内部的 full attention,同时保留 chunk 之间的因果依赖关系。对于第 个 chunk,计算公式为:

其中,inter-chunk 组件通过 sequential hidden state \mathbf 保持因果关系,而 intra-chunk 组件在当前 chunk 内实现 full attention。
添加 gate 机制
Gate 机制常用于增强线性注意力。本文发现使用标量 decay term,可以在享受更快的训练速度的同时足以产生良好的性能。同时,本文令 gate 变为 data-dependent 的。
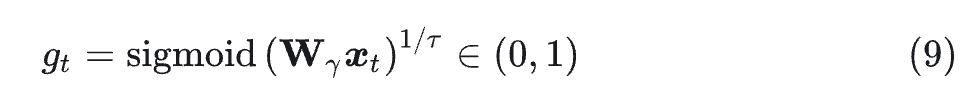
其中, 是每个步骤的输入。在 chunk 中,计算门控值的几何平均值以获得 chunk-level 的衰减:
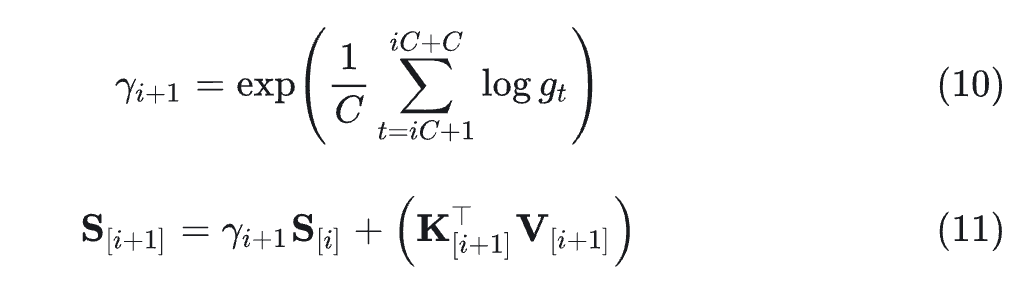
输出计算保持不变。
1.5 实验结果
Flow Setting
使用与 SiT 中相同的 Stable Diffusion 的预训练 VAE 模型来编码图像,为大小为 的输入图像生成维度为 的表征。 使用线性插值时间表,其中 和 。
生成过程中,SDE solver 使用 first-order Euler-Maruyama integrator,并将生成步数限制为 250,与 SiT 中使用的采样步骤一致。除非另有说明,否则所呈现的所有指标都是在 ImageNet 数据集上评估的 FID-50K 分数。
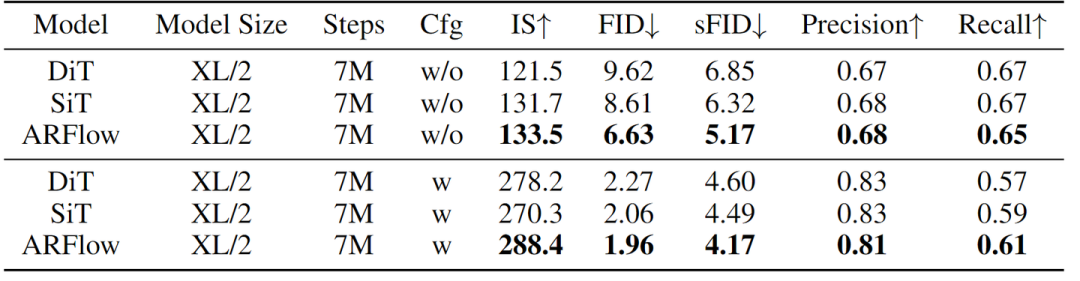
图 3 展示了在不同 CFG 条件下 ImageNet 256×256 数据集上的 ARFlow、SiT 和 DiT 模型的性能比较。
在没有 CFG 的情况下,ARFlow 始终优于 DiT 和 SiT。在 CFG 条件下,ARFlow 进一步扩展了其优势,展示了最高的 IS (288.4) 和最低的 FID (1.96) 和 sFID (4.17)。这些结果清楚地表明,与基线模型相比,ARFlow 在生成高质量的图像方面具有出色的能力。
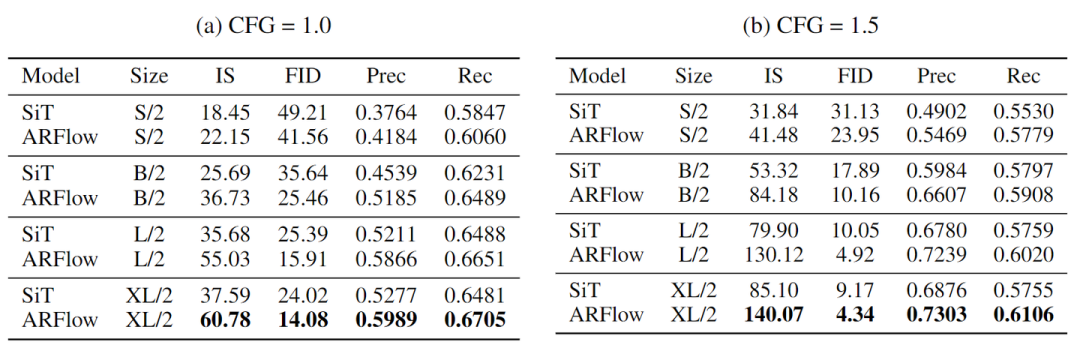
作者将 ARFlow 与 SiT 在不同模型尺度和 CFG 设置下在 ImageNet 128×128 上进行比较。ARFlow 在所有模型尺度和指标上都始终优于 SiT。
在不用 CFG (CFG=1.0) 的情况下,ARFlow-XL/2 实现了 14.08 的 FID 和 60.78 的 IS,大大改进了 SiT-XL/2 的 24.02 的 FID 和 37.59 的 IS。使用 CFG=1.5 的情况下,改进更为明显 – ARFlow-XL/2 达到 4.34 的 FID 和 140.07 的 IS,与 SiT-XL/2 相比,相对 FID 提高了 52.67%。增强的 Precision/Recall 指标展示了样本质量和多样性的改进。
可视化 ARFlow Scale
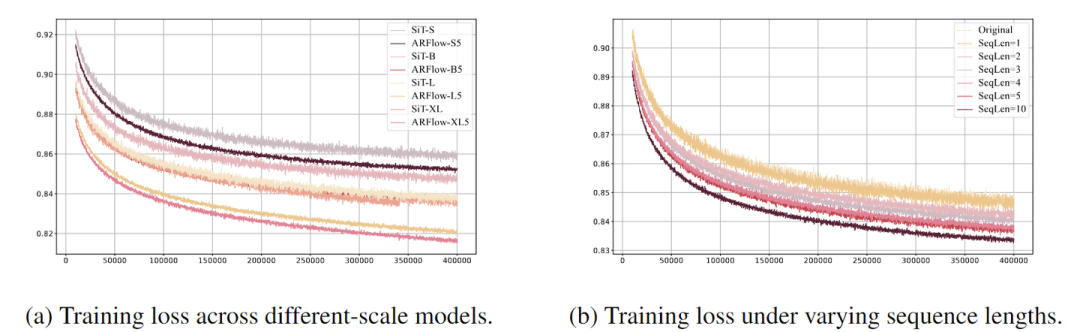
如图 5(a) 所示,我们可视化了不同尺度的 SIT 和 ARFlow 的训练损失,可以发现对于相同的模型大小,ARFlow 的损失低于原始 SiT,特别是 ARFlow-B5 的损失接近 SiT-XL 的损失。
可视化 Sequence Length
图 5(b) 说明了随着 ARFlow 的序列长度的增加,模型性能的逐步改进。
训练损失曲线展现出清晰的趋势:较长的序列长度始终导致较低的训练损失。从序列长度为 1 开始,与原始 SiT 模型具有相似的损失,序列长度的每个增加都会导致训练损失显着减少,序列长度为 10,达到最低损失。
作者还在图 6 中可视化了使用不同序列长度训练的 ARFlow 的样本。结果表明,随着序列长度的增加,模型的性能有所提高。

去除 Cache State
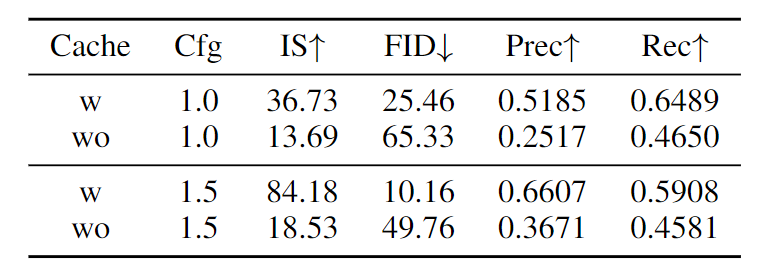
图 7 显示了一项消融实验,该研究检查了缓存状态在我们的混合线性注意力中的重要性。我们将我们的完整模型与删除块之间的隐藏状态转移的变体进行比较,有效地消除了时间记忆机制。结果清楚地表明缓存状态在保持生成质量方面的关键作用。
在 CFG=1.0 时,删除 cached states 会导致所有指标的性能显着下降。FID 从 25.46 增加到 65.33,而 IS 从 36.73 急剧下降到 13.69。当应用 CFG (CFG=1.5) 时,这种显着性能差距变得更加明显,完整模型实现了 10.16 的 FID,而没有 cached states 只有 49.76。Precision (0.607 到 0.3671) 和 Recall (0.5908 到 0.4581) 指标的严重退化表明缓存的状态机制对于生成质量和多样性都是必不可少的。还表明模型学习到了步骤间传递的语义信息。
参考
-
^Gated linear attention transformers with hardware-efficient training
(文:极市干货)

