
四个月前,我们发布了 Moonlight [1],在 16B 的 MoE 模型上验证了Muon优化器的有效性。在 Moonlight 中,我们确认了给 Muon 添加 Weight Decay 的必要性,同时提出了通过 Update RMS 对齐来迁移 Adam 超参的技巧,这使得 Muon 可以快速应用于 LLM 的训练。
然而,当我们尝试将 Muon 进一步拓展到千亿参数以上的模型时,遇到了新的“拦路虎”——MaxLogit 爆炸。
为了解决这个问题,我们提出了一种简单但极其有效的新方法,我们称之为“QK-Clip”。该方法从一个非常本质的角度去看待和解决 MaxLogit 现象,并且无损模型效果,这成为我们最新发布的万亿参数模型“Kimi K2”[2] 的关键训练技术之一。

问题描述
我们先来简单介绍一下 MaxLogit 爆炸现象。回顾 Attention 的定义:
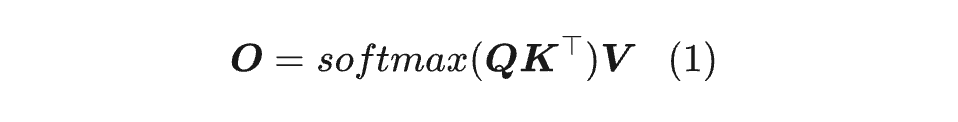
这里省略了缩放因子 ,因为它总可以吸收到 的定义中。“MaxLogit 爆炸”中的 Logit,指的是 Softmax 前的 Attention 矩阵,即 ,而 MaxLogit 指的是全体 Logit 的最大值,我们将它记为:
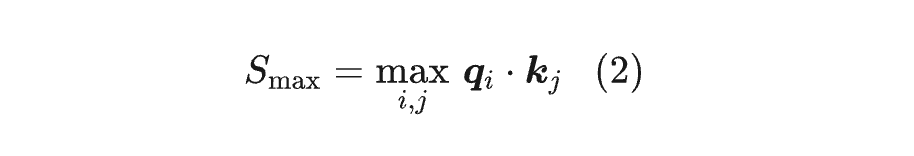
这里的 其实还要在 batch_size 维度上取,最终得到一个标量。而 MaxLogit 爆炸是指, 随着训练的推进一直往上涨,增长速度是线性甚至是超线性的,并且在相当长的时间内没有稳定的迹象。
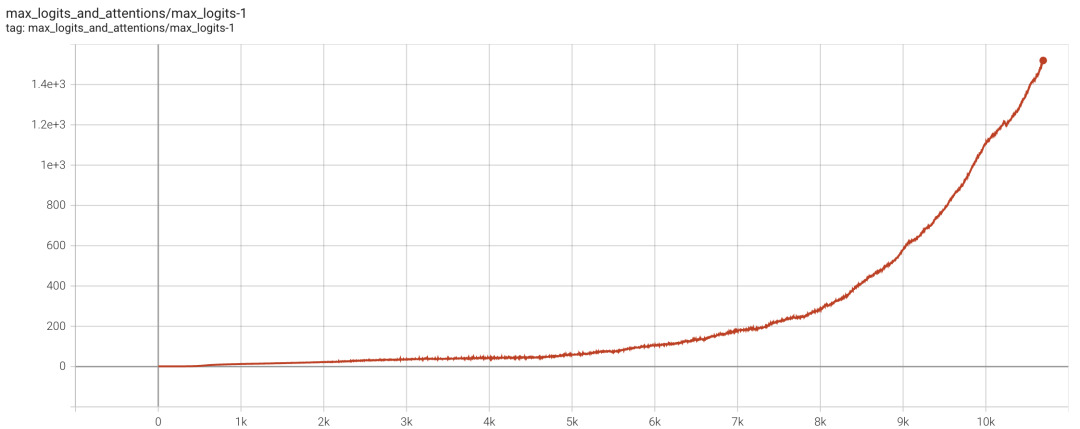
▲ MaxLogit爆炸现象
MaxLogit 本质上是一个异常值指标,它的爆炸意味着异常值超出了可控范围。具体来说,我们有:
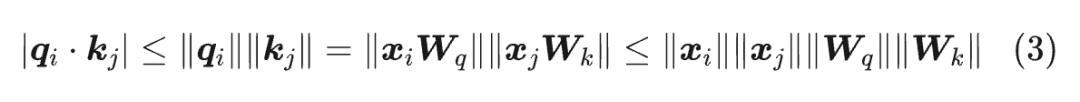
由于 通常会加 RMSNorm,所以一般情况下 是不会爆炸的,因此 MaxLogit 爆炸意味着谱范数 有往无穷大发展的风险,这显然不是一个好消息。
由于再大的数值经过 Softmax 后都变得小于 1,所以比较幸运的情况下,这个现象不会带来太严重的后果,顶多是浪费了一个 Attention Head,但比较糟糕的情况下,可能会引起 Grad Spike 甚至训练崩溃。因此,保险起见应当尽量避免 MaxLogit 爆炸的出现。

已有尝试
在《Muon续集:为什么我们选择尝试Muon?》[1] 中我们简单分析过,Weight Decay 能一定程度上预防 MaxLogit 爆炸,所以小模型出现 MaxLogit 爆炸的概率很小,即便像 Moonlight 这样的 16B 模型,MaxLogit 最多涨到 120 后就自动降下来了。
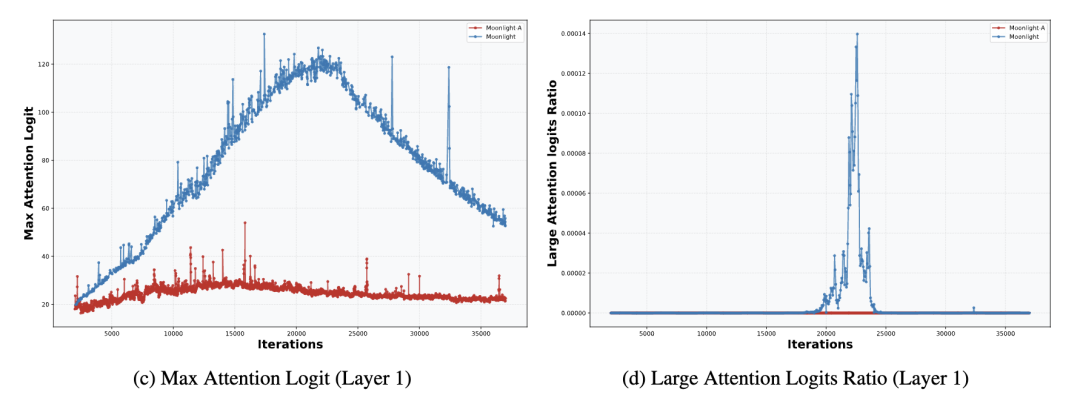
▲ Moonlight的MaxLogit自动降了下来
换句话说,MaxLogit 爆炸更多出现在非常大参数量的模型中,模型越大,训练的不稳定因素越多,Weight Decay 越难稳定训练。这时候增加 Weight Decay 自然也能加强控制,但同时也会带来明显的效果损失,所以此路不通。
另一个比较直接的思路是直接给 Logit 加 :

其中 ,由 Google 的 Gemma2 [3] 引入。由于 的有界性, 自然是能够保证 后的 Logit 有界的,但无法保证 前的 Logit 是有界的(亲测),所以 只是将一个问题转化为了另一个问题,实际上并没有解决问题。
也许 Google 自己都意识到了这一点,所以在后来的 Gemma3 [4] 中没有用 了,而改用“QK-Norm”:
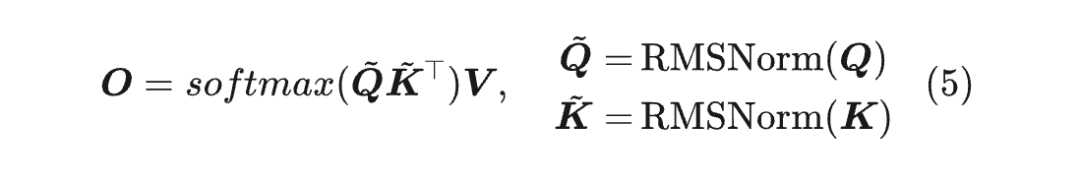
QK-Norm 确实是压制 MaxLogit 非常有效的方法,然而它只适用于 MHA、GQA 等,不适用于 MLA,因为 QK-Norm 需要把 给 Materialize 出来。
但对于 MLA 来说,它训练阶段跟 Decoding 阶段的 并不一样(如下式所示),在 Decoding 阶段我们没法完全 Materialize 训练阶段的 ,换言之,Decoding 阶段没法做 QK-Norm。

为什么要用 MLA?我们已经用文章《Transformer升级之路:MLA好在哪里?》讨论了这个问题,这里不再重复。总之,我们希望 MLA 也能有类似 QK-Norm 的能够保证压制 MaxLogit 的手段。

直击目标
期间我们还尝试了一些间接手段,比如单独降低 的学习率、单独增大它们的 Weight Decay 等,但都不奏效。
最接近成功的一次是 Partial QK-Norm,对于 MLA 来说,它的 分为 qr、qc、kr、kc 四个部分,其中前三部分在 Decoding 时都是可以 Materialize 的,所以我们给这三部分都加上 RMSNorm,结果是可以压制 MaxLogit,但长度激活效果非常糟糕。
在失败多次之后,我们不禁开始反思:前面我们的尝试其实都只是压制 MaxLogit 的“间接手段”,真正能保证解决 MaxLogit 爆炸的直接手段是什么?
从不等式(3)我们不难联想到可以对 做奇异值裁剪,但这本质上还是间接手段,而且奇异值裁剪的计算成本也不低。
但很明显,对 进行事后缩放理论上是可行的,问题是什么时候缩放、缩放多少。
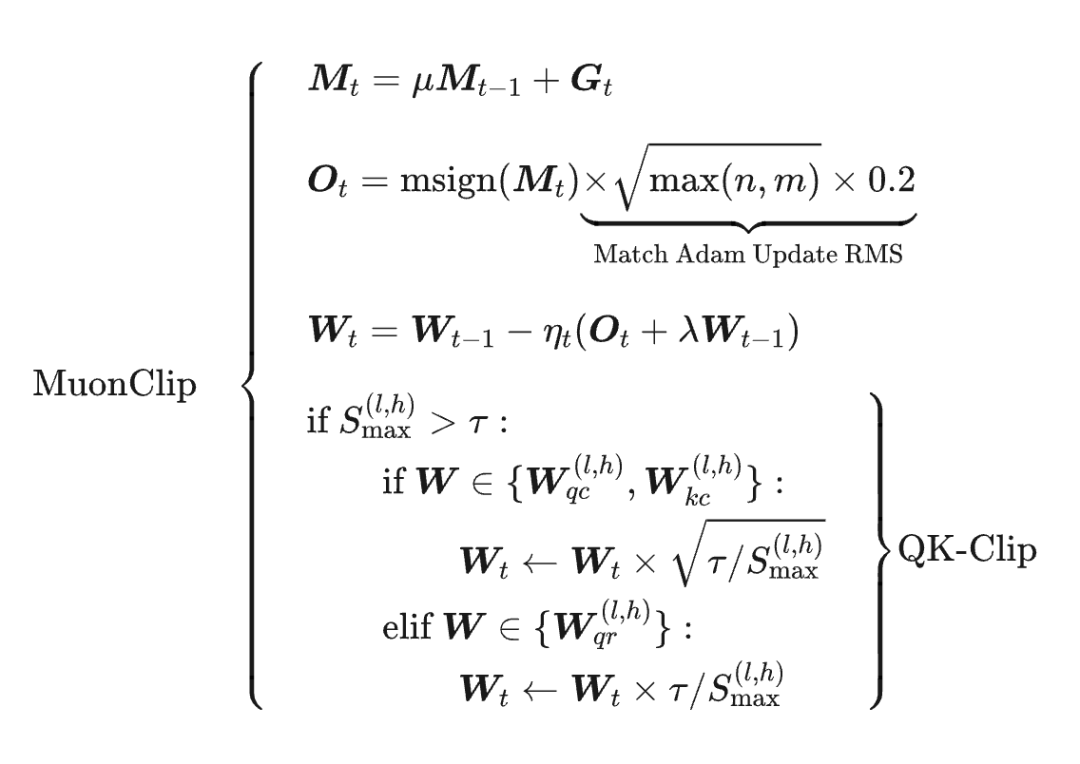
终于,某天福至心灵之下,笔者总算反应过来:MaxLogit 本身就是触发缩放的最直接信号!具体来说,当MaxLogit 超过期望阈值 时,我们直接给 乘上 ,那么新的 MaxLogit 肯定就不超过 了。
乘 的操作,我们可以分别吸收到权重 的权重上去,于是我们得到初版 QK-Clip:
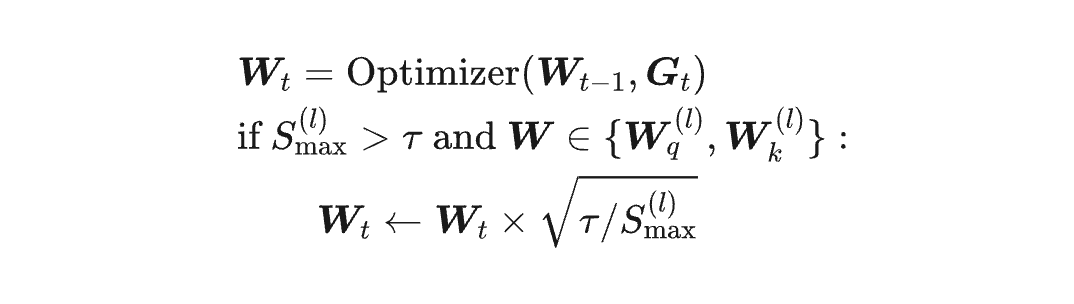
其中 是第 l 层 Attention 的 MaxLogit, 是它 的权重。
也就是说,在优化器更新之后,根据 的大小来决定是否对 的权重进行裁剪,裁剪的幅度直接由 与阈值 的比例来决定,直接保证裁剪后的矩阵不再 MaxLogit 爆炸。
同时,由于是直接对权重进行操作,所以不影响推理模式,自然也就兼容 MLA 了。

精细调整
初版 QK-Clip 确实已经能成功压制 MLA 的 MaxLogit,但经过仔细观察模型的“内科”后,我们发现它会出现“过度裁剪”的问题,修复该问题后就得到最终版 QK-Clip。
我们知道,不管哪种 Attention 变体都有多个 Head,一开始我们是每一层 Attention 只监控一个 MaxLogit 指标,所有 Head 的 Logit 是放在一起取 Max 的,这导致 QK-Clip 也是所有 Head 一起 Clip 的。
然而,当我们分别监控每个 Head 的 MaxLogit 后发现,实际上每层只有为数不多的 Head 会出现 MaxLogit 爆炸,如果所有 Head 按同一个比例来 Clip,那么大部份 Head 都是被“无辜受累”的了,这就是过度裁剪的含义。
简单来说,QK-Clip 的操作是乘以一个小于 1 的数,这个数对于 MaxLogit 爆炸的 Head 来说是刚刚好抵消增长趋势,但是对于其他 head 来说是单纯的缩小(它们没有增长趋势或者增长趋势很弱)。
由于长期无端被乘一个小于 1 的数,那么很容易出现就趋于零的现象,这是“过度裁剪”的表现。
所以,为了避免“殃及池鱼”,我们应该 Per-Head 地进行监控 MaxLogit 和 QK-Clip。
不过这里边又隐藏了另一个魔鬼细节:初版 QK-Clip 是将 Clip 因子平摊到 上的,但是 MLA 的 有 qr、qc、kr、kc 四部分,其中 kr 是所有 Head 共享的,如果对它 Clip,那么同样会有“殃及池鱼”的问题。
因此,对于 (qr, kr),我们应该只 Clip 到 qr 上去。
经过上述调整,最终版的 QK-Clip 为:
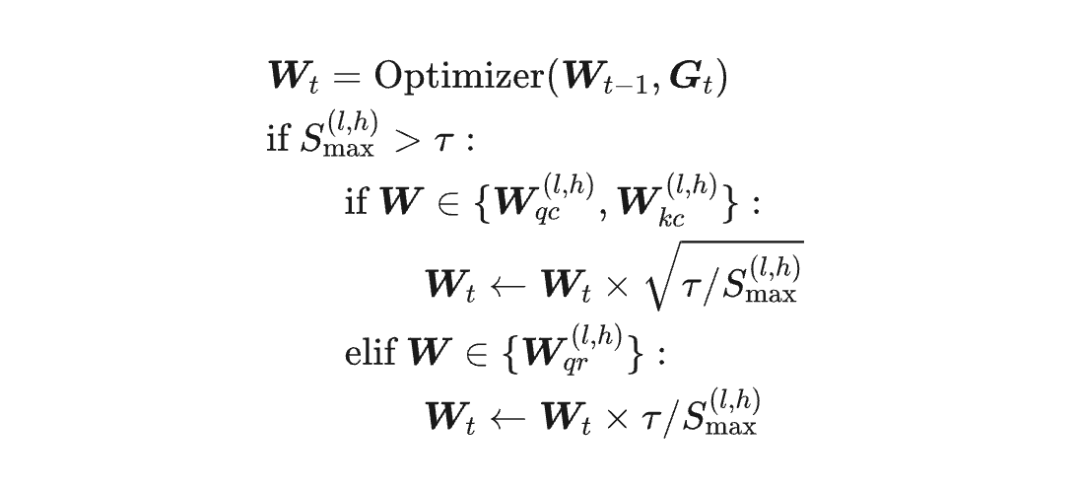
其中上标 表示第 l 层、第 h 个 Head。

扩展之路
至此,QK-Clip 的操作细节已经介绍完毕,它直接以我们期望的 MaxLogit 为信号,对 的权重进行尽可能小的改动,达到了将 MaxLogit 值控制在指定阈值内的效果。同时因为这是直接对权重进行修改的方法,所以它兼容性比 QK-Norm 更好,可以用于 MLA。
在 Kimi K2 的训练中,我们设置阈值 为 100,总训练步数约为 220k steps,从大致 7k steps 开始,就出现了 MaxLogit 超过 的 Head,此后在相当长的时间内,Muon Update 和 QK-Clip 都在“拉锯战”,即 Muon 想要增加 MaxLogit 而 QK-Clip 想要降低 MaxLogit,它们一直处于微妙的平衡状态。
有趣的是,70k steps 之后,所有 Head 的 MaxLogit 都主动降低到了 100 以下,QK-Clip 不再生效。
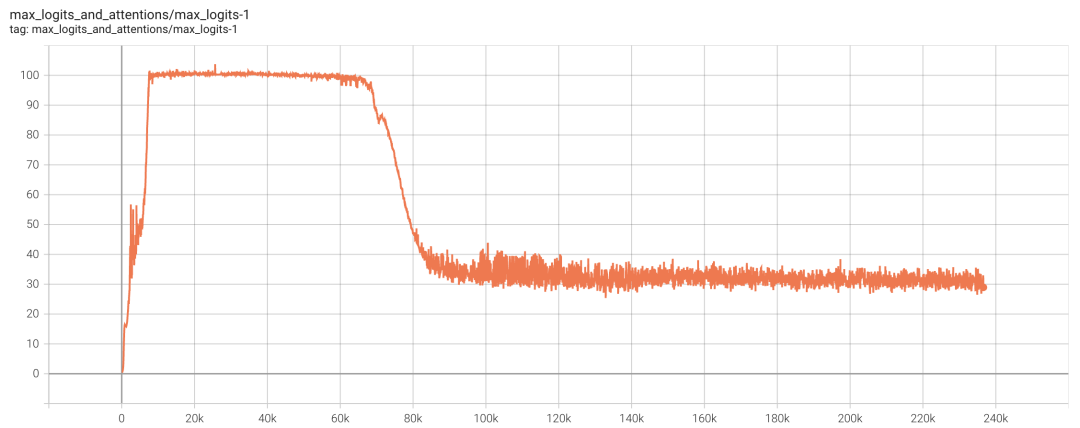
▲ 经过接近70k steps的Muon和QK-Clip拉锯战后,MaxLogit主动降了下来
这表明,在 Weight Decay 的作用下,只要我们能稳住训练,模型最后很可能都会主动将 MaxLogit 降下来,QK-Clip 的作用,正是帮助模型更平稳地度过训练初期。
可能有读者担心 QK-Clip 会有损效果,但我们在小模型上做了对比实验,即便通过 QK-Clip 将 MaxLogit 压得特别小(比如 30),也没有观察到效果有实质区别,再加上中后期模型会主动将 MaxLogit 降下来的这一现象,我们有理由相信 QK-Clip 对效果是无损的。
我们在实验中也观察到,Muon 普遍比 Adam 更容易 MaxLogit 爆炸,所以某种程度上来说,QK-Clip 是专门为 Muon 补充的更新规则,它是 Muon 在超大规模训练上的“通关秘笈”之一,这也是本文标题的含义。
为此,我们将我们 Moonlight 中所提的 Muon 改动跟 QK-Clip 组合起来,起了个“MuonClip”的名字():
注意,“Muon 普遍比 Adam 更容易 MaxLogit 爆炸”并不意味着只有 Muon 会 MaxLogit 爆炸,我们知道 DeepSeek-V3 是 Adam 训练的,而我们从 DeepSeek-V3 的开源模型中也观察到了 MaxLogit 爆炸现象,还有 Gemma2 用 防止 MaxLogit 爆炸,它也是 Adam 训的。
因此,虽然我们强调了 QK-Clip 对 Muon 的价值,但如果读者坚持用 Adam,那么它也是可以跟 Adam 结合成 AdamClip 的。

为什么 Muon 更容易导致 MaxLogit 爆炸呢?这一节笔者尝试给出一个理论角度的解释,供大家参考。
从不等式(3)可以看出,MaxLogit 爆炸往往意味着 或 的谱范数出现爆炸的迹象,实际上谱范数的定义中也包含了取 操作,两者本质上是相通的。
因此,问题可以转化为“为什么 Muon 更容易导致谱范数爆炸”。我们知道谱范数等于最大的奇异值,所以又可以进一步联想到“为什么 Muon 更倾向于增大奇异值”。
Muon 和 Adam 的区别是什么呢?
Muon 给出的更新量是经过 运算的,所有奇异值都相等,即它的有效秩是满秩;而一般情况下的矩阵,奇异值通常都是有大有小,并且以前面几个奇异值为主,从有效秩的角度看它们是低秩的,我们对 Adam 更新量的假设也是如此。这个假设并不新鲜,比如高阶 muP 同样假设了 Adam 更新量的低秩性。
用公式来说,我们设参数 的 SVD 为 ,Muon 更新量的 SVD 为 ,Adam 更新量 的SVD 为 ,那么:
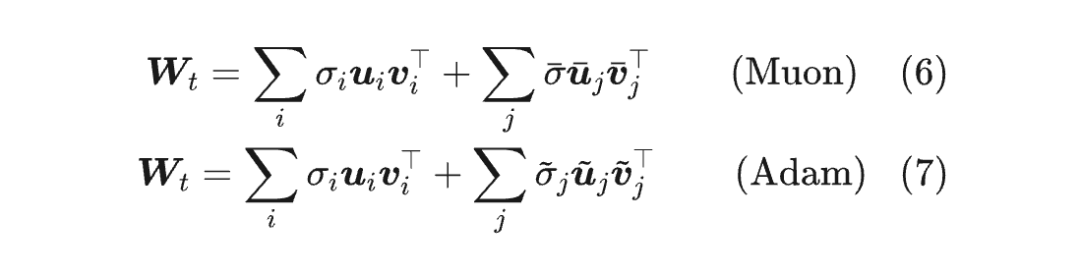
很明显,如果奇异向量对 跟某个 或 很接近,那它们将会直接叠加起来,从而增大 的奇异值。由于Muon的更新量是满秩的,所以它与 的“碰撞几率”会远大于Adam的,所以Muon更容易增大参数的奇异值。
当然,上述分析是通用的,不限于 的权重,实际上在Moonlight中我们已经验证过,Muon训出来的模型权重的奇异值熵普遍更高,这也佐证了上述猜测。
Attention Logit 的特殊之处在于,它是双线性形式 , 的连乘使得爆炸的风险更大,还容易导致“糟的更糟”的恶性循环,最终促成了 MaxLogit 爆炸。
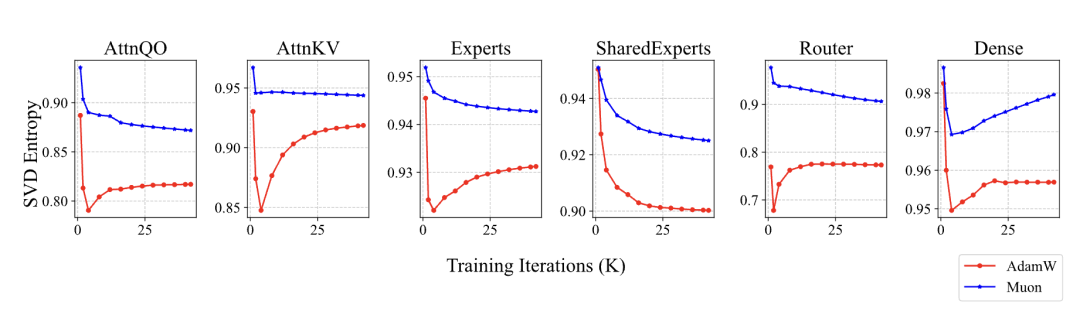
▲ Muon与Adam训练的模型权重奇异值熵(等价于有效秩)比较
最后就是“Muon 的碰撞几率远大于 Adam”是相对而言的,实际上奇异向量碰撞在一块还是小概率事件,这也就能解释为啥只有小部份 Attention Head 会有 MaxLogit 爆炸现象了。
这个视角还可以解释之前 Moonlight 的一个现象:用 Muon/Adam 预训练的模型,反过来用 Adam/Muon 微调,结果通常是次优的。
因为 Muon 的训练权重有效秩更高,而 Adam 的更新量是低秩的,一高一低之下,微调效率就变差了;反之,Adam 的训练权重有效秩更低,但 Muon 的更新量是满秩的,它有更大概率去干预那些小奇异值分量,让模型偏离预训练的低秩局部最优点,从而影响微调效率。

写到这里,关于 QK-Clip 比较重要计算和实验细节应该都讲清楚了。另外还需要提醒的是,QK-Clip 思想很简单,但由于需要 Per-Head 来 Clip,因此在分布式训练中写起来还是略微有点难度的,因为此时的参数矩阵往往被切分得“支离破碎”(在 Muon 基础上改起来不算难,在 Adam 基础上改则稍显复杂)。
对于笔者及其团队来说,QK-Clip 不单单是解决 MaxLogit 爆炸问题的一个具体方法,还是反复尝试通过间接手段来解决问题且失败后的一次”幡然醒悟“:
既然有了明确的度量指标,那么我们应该寻求能够保证解决问题的直接思路,而不是在降低 LR、增大 Weight Decay、部分 QK-Norm 等可能但不一定能解决问题的思路上浪费时间。
从方法上来看,QK-Clip 的思路也不限于解决 MaxLogit 爆炸,它可以说是解决很多训练不稳定问题的“抗生素”。
所谓抗生素,指的是它也许并不是解决问题最精妙的方法,但往往是解决问题最直接有效的方法之一,QK-Clip 正是具有这个特点,它可以一般地推广成“哪里不稳 Clip 哪里”。
比如,有些情况下模型会出现“MaxOutput 爆炸”的问题,这时候我们可以考虑根据 MaxOutput 的值来 Clip 权重 。
类比 QK-Clip 的 Per-Head 操作,这里我们也需要考虑 Per-Dim 操作,但 Per-Dim Clip 的成本显然太大,可能需要折中一下。总之,“哪里不稳 Clip 哪里”提供了统一的解决思路,但具体细节就要看大家发挥了。
最后,QK-Clip 这种根据某些信号手动制定更新规则的操作,一定程度上是受到了 DeepSeek 的 Loss-Free 负载均衡策略的启发而悟到的,这里再次致敬 DeepSeek!

本文提出了 QK-Clip,它是 MaxLogit 爆炸问题的一种新思路,跟 QK-Norm 不同,它是对 Q、K 权重的一种事后调整方案,并不改变模型的前向计算,因此适用性更广,它是“Muon + MLA”组合在超大规模训练上的重要稳定策略,也是我们最新发布的万亿模型 Kimi K2 的关键技术之一。
(文:PaperWeekly)


