简单介绍一下最近在Seed的工作,希望能够抛砖引玉.
https://arxiv.org/pdf/2505.19488 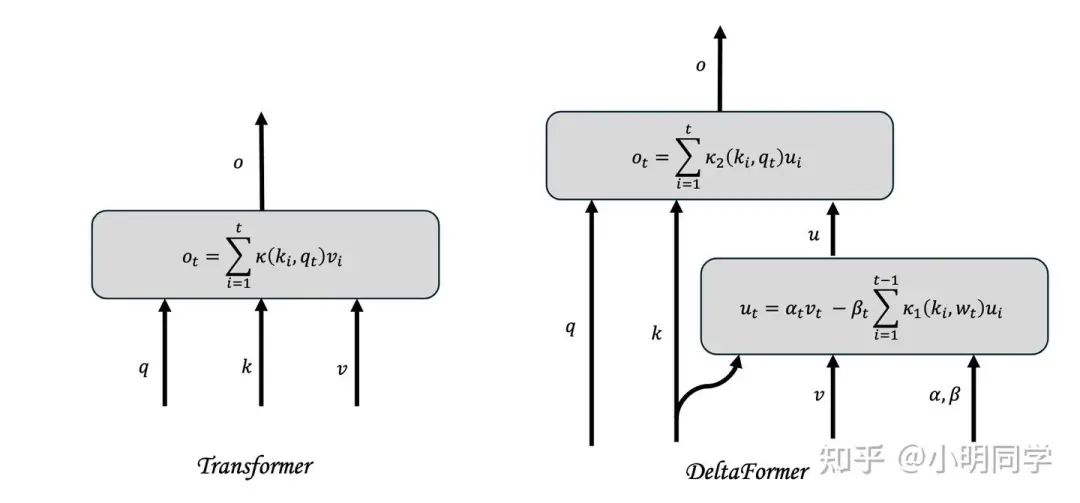
Motivation
表达性和不可并行性之间有本质矛盾
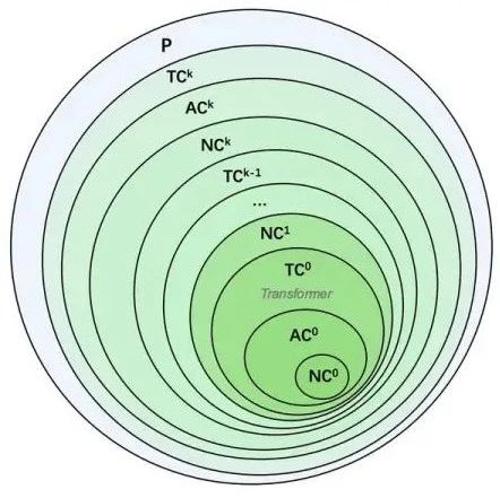
从high level的角度来说,表达性和可并行之间存在着不可调和的矛盾。一些问题的正确结果的输出,在客观上就需要一定的深度,通俗来讲,解题的时候,有些步骤是可以并行着做的,但有些关键步骤必须得一步一步来,而这些关键步骤的最大长度如果低于一个下界,那么也就不可能得到正确的答案。为此,上个世纪研究计算复杂度的科学家们,也开始关注到并行复杂度。他们在P类的问题中,根据单个节点允许的操作类型,单个节点允许的扇入和整个计算图的关键路径长度,在P问题中,划分出了若干类,譬如 .
LSTM和Transformer之间或许非常空旷大有作为
上个世纪末开始火的LSTM是一个本质不可并行的P模型。但最近十年。GPU重新定义了环境,让高并行的Transformer模型成为了现如今大模型领域最为流行的骨架。与此同时,并行性和表现力上的根本性矛盾也导致大模型的缺陷,譬如数数能力的缺陷,必须依赖Chain-of-thought才能解决复杂问题。
那么,难道没有一个依然可以高度可并行,只是并行程度比Transformer稍差一点,但表现力更高的架构吗?前人告诉我们在 和 之间还存在着大量的复杂度类,这给我们的遐想带来了空间。或许真的存在也能在GPU上高并行实现的,且比Trasnformer更有表现力的模型。
复杂度模型的复苏
相比于Transformer和Linear attention无视之前的状态,无脑写入或者append key和value的做法不同,Delta rule会考虑每次写入的时候,根据之前的状态进行修改。这个事情在上个世纪研究的还挺多的,包括Schmidhuber[1], Sutton[2]还有Hinton[3], 虽然那个时候的名称叫做fast weight programming,但内核是一致的。2021年Schimidbuber[4]还重提了一次。但在GPU的时代下,一个难以在GPU上高度并行的实现方式,是没法成为下一代模型,否则直接退回LSTM模型,不停加大hidden size就好了。2024年,Songlin Yang[5]等发现了Delta rule的并行潜力,将DeltaNet在GPU上并行起来,这也让Delta rule复苏了。而这一模型是一个能够达到 复杂度的模型,因此能在State tracking相关的任务上表现良好.
Transformer + Delta rule = Deltaformer
DeltaNet的受制于有限状态空间,其最基本的长文信息检索能力有限,而Transformer的长文信息检索能力则比较棒。将两者有机的融合,寻求一个完全超过Transformer架构的模型则是我们这个工作的目的。
Method
Deltaformer = Deltarule + Kernel trick
Kernel trick也是一个古老的方法,从SVM的时代中,Kernel SVM也就占据了一席之地。这种将特征隐式地拓展到无穷维的方法,或许是一个增加记忆容量的好方法。
引入Kernel: , 其中 是一个从有限维映射到无穷维的一个映射,我们一般不把它显式写出来。那么我们给Delta rule重写如下:
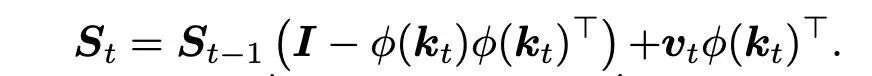
最大的问题在于这里面的 和 S 都是无穷维的,没法在计算机上运算。
好在经过一些推导,可以将 和 S 这些涉及到无穷的东西都给消去了,只保留了 。
写入方式为:
读出方式为:
当然也可以给里面做一些其他的事情,譬如上面和下面的 采用不一样的,以及加一些可学习的参数之类的。
我们使用softmax来当 ,那么我们也就得到了Transformer的Deltarule的升级版。
接下来则要回答两个问题:
-
• 1) 怎么在GPU上高效实现 -
• 2)怎么证明这样表达式能做 的任务
Chunk-wise algorithm
难的部分在于 的计算,而 的计算则正常使用Flash attention即可。
直接使用 在decode阶段可以这么做,但模型训练的时候,这样的递归算,还不如搞非线性RNN.
但我们也可以写成更加紧凑的形式: , 其中
那么有 ,直接搞这么大的矩阵求逆,虽然并行度高,但I/O支持不了.
c为下标表示是current chunk的对应变量,p为下标表示previous的变量,因此有:
故而:
利用这种方法可以逐chunk地计算 . 如果序列长度是 , chunk size是 ,head dim 是 ,用的是前代法求逆,那么总的Flops是
Can track the exchange of n elements.
我们理论证明这个模型架构的上限是能够到达 的。我们研究了追踪 n 个元素交换这一任务,这是一个 . 我们采用了构造性的方式进行了证明,具体证明可以参见原论文。结论是能够以 的head dim来追踪 个物体的交换。

Experiment
大规模的语言任务在scaling,以后有机会再更新。还是从个人更钟爱的Toy 任务来分享吧。
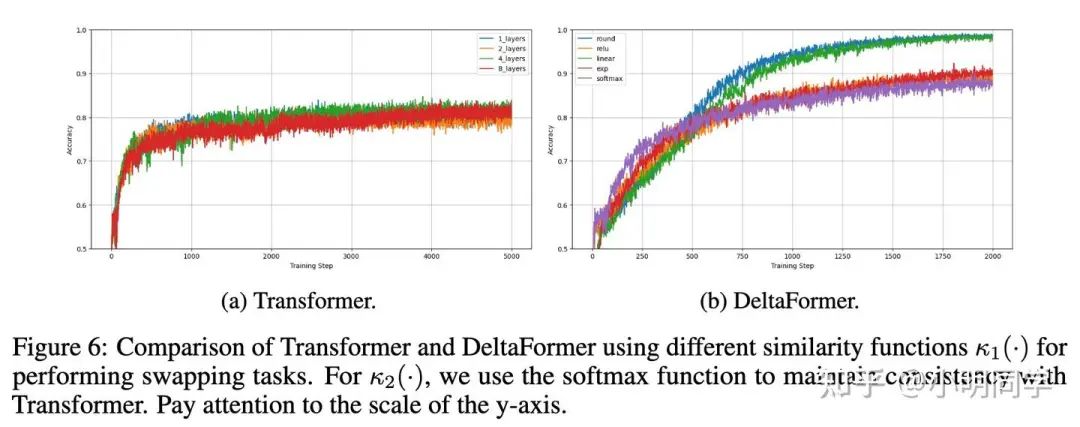
Deltaformer 可以追踪swap,但Transformer很难
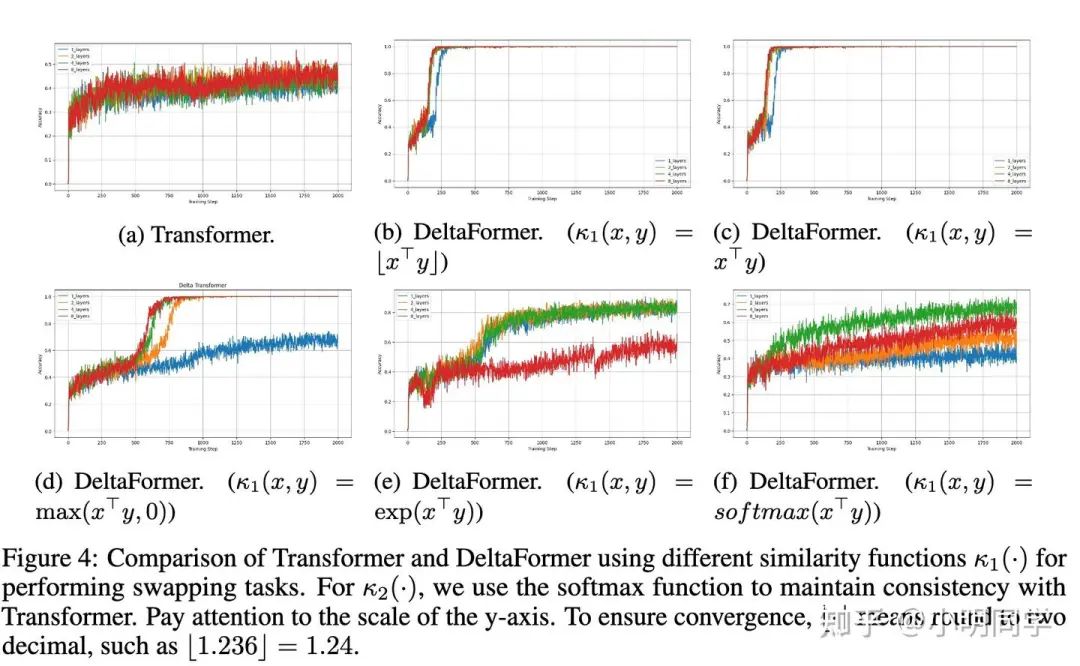
譬如我们可以发现Transfomer想要追踪5个元素的交换还是挺难的. 但核函数的选择对做 还是挺重要的.
Deltaformer 可以进行有向无环图的连通性判断
也挺合理的,因为Deltaformer里面的求逆操作 , 如果编码了i节点和j节点是否是相邻节点,那么也就编码了节点和节点是否是k步可达的。那么编码了i节点和j节点的是否连通的信息。(从另一个角度来说,也是因为求逆这一远超 的操作拓展了Transformer的表现力。
更多toy model的实验和有趣的现象可以参考我们的原论文.
Conclusion
我们提出了Deltaformer这一模型,它拥有了Transformer模型的记忆力和能够在GPU上高效训练的特性,同时还突破了Transformer的 表现力限制。希望可以为以后设计更高表现力的模型抛砖引玉。
引用链接
[1] Schmidhuber: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=2f0becffd2f44b198d28074d01722e4c7905dae2[2] Sutton: https://web.cs.umass.edu/publication/docs/1980/UM-CS-1980-018.pdf[3] Hinton: https://www.cs.toronto.edu/~fritz/absps/fastweights.pdf[4] Schimidbuber: https://proceedings.neurips.cc/paper_files/paper/2021/file/3f9e3767ef3b10a0de4c256d7ef9805d-Paper.pdf[5] Songlin Yang: https://arxiv.org/pdf/2406.06484
(文:机器学习算法与自然语言处理)