机器之心报道
编辑：Panda
在根据某个奖励微调生成式语言模型时，使用 KL 正则化的强化学习（KL-RL）来对齐生成式语言模型是一种常用框架。而 KL-RL 通常需要训练一个奖励模型，然后使用一个强化学习求解器。其它方法还包括直接偏好优化、奖励模型蒸馏、best-of-N 蒸馏的不同变体版本。
在度量 KL-RL 框架的效果时，常用的指标是已对齐模型相较于参照模型在给定任务上的胜率。
但是，在推理时间很少会使用已对齐的模型，而是会通过一个推理时间流程来完成任务，比如 best-of-N 采样、best-of-N 越狱、思维链推理、自我一致性。这样一来，推理时间解码过程与训练 KL-RL 目标之间就不匹配了。
于是，问题来了：给定一个已知的推理时间流程，我们可以对齐模型，从而优化相对于参照模型的推理时间胜率吗？其中，为了求取推理时间胜率，需要通过该推理时间流程获取每个模型的响应并统计每个模型的样本获胜次数。
Google DeepMind 和 Google Research 近日的一篇论文尝试解答了这个问题。他们发现，尽管很难直接优化推理时间胜率，但可通过一组优化目标来获取其最优解。该团队将这个框架称为 inference-aware alignment (InfAlign)，即推理感知型对齐。
-
论文标题：InfAlign: Inference-aware language model alignment -
论文地址：https://arxiv.org/abs/2412.19792
他们还进一步证明，对于被 δ 限定的语言模型（其中随着 δ → 0，所有输出都被 δ 限定了上限），可通过对奖励使用一个特定的变换来求解 KL-RL，从而得到这个最优解。
如此一来，针对推理时间胜率进行优化的难题就可以这样解决了：设计一个适合特定推理时间流程的奖励变换，然后使用 PPO 等已有的优化算法来求解 KL-RL。
使用奖励变换实现强化学习
为了解决以下定义 5 中的语言模型对齐问题，该团队提出了一个通用框架。
定义 5：令 T 为一个给定的推理时间流程，且 β > 0。那么，最大化推理时间胜率的优化问题就可以表述成
他们提出的新方法的基础是：基于奖励模型 r、推理时间流程 T、基础策略 π_ref 设计一个新的奖励函数 R；这样一来，解决带有已变换奖励 R 的 KL 正则化强化学习问题就基本上能得到一个最优解。更确切地说，已对齐策略就是以下优化问题的解：
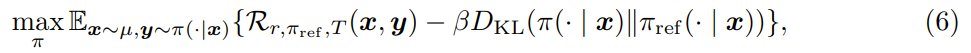
其中 R 是变换后的奖励函数。大致看的话，可能不太容易理解为什么 (6) 式可帮助求解 (5) 中的问题。但该团队会证明，对于任意给定的推理时间流程 T ，都存在一个可解决 (5) 的变换后奖励 R。
定理 1（InfAlign 解决方案的特征）假设 T 使得对于所有 x、y_1、y_2 都存在 ∂T (π)(y1 | x)/∂π(y_2 | x)，则就得到了最优转换奖励 R，并且 (5) 式中的最优策略 π∗ 必须满足以下耦合方程：∀x, y
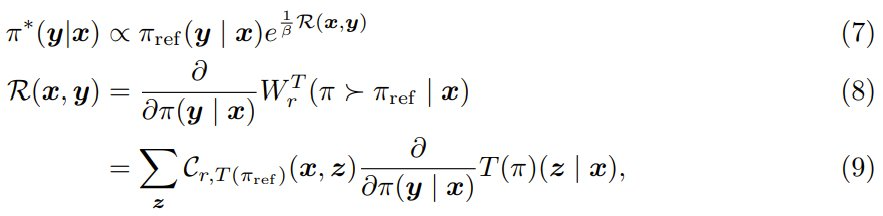
其中 
是该推理时间转换策略下已校准的奖励。
对该定理的证明请访问原论文。而基于该定理，可以自然地得到一个迭代 EM 式算法，其可以根据 (7) 式使用固定的 R 更新 π，并可以根据 (9) 式使用固定的 π 来更新 R，直到收敛。
然而，这种算法有两个缺点：首先，对于一般的语言模型，难以评估方程 (9) 或者评估效率很低，因为这需要在巨大甚至无限的输出空间上评估策略；其次，尚不清楚这种算法是否能得到最优解。
为了更高效地设计奖励变换，该团队研究了不执行推理时间流程的情况。在这种情况下，在这种情况下，T (π) = π 且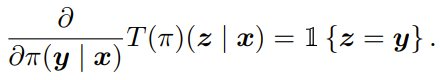 
(9) 式便可简化为 R (x, y) = C_{r,π_ref} (x, y)，即 π_ref 下的 CDF 或已校准奖励。
因此，定理 1 可以看作是这些结果与一般推理时间流程的泛化。这一观察促使该团队考虑基于此已校准奖励的一系列奖励变换，如下一节所述。我们将看到，对于这类已校准推理时间流程（定义 6），可以通过一个实验性语言模型有效地评估此系列中的不同变换，从而找到优良甚至最佳的变换。
解决 InfAlign
使用已校准奖励实现 KL-RL
对已校准奖励 C_{r,π_ref} 的性质的讨论请访问原论文。接下来看如何在 KL 正则化的强化学习中使用这个已校准奖励。
根据其性质，校准之后，基础策略的输出的奖励分布独立于奖励模型与基础策略本身。这样一来，便可以设计一个仅关注推理时间流程 T 的变换函数 Φ，并将其用于已校准奖励函数。
更确切地说，令 Φ : [0, 1] → ℝ 为一个变换函数，该团队提出了以下奖励函数：
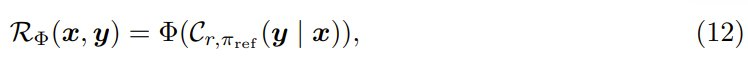
而我们希望已对齐策略是 KL-RL 问题的解。
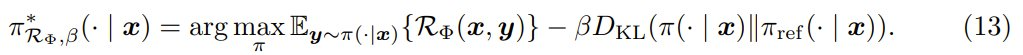
推理感知型奖励变换。对于给定的推理时间流程 T ，目标是推导或设计一个合适的变换 Φ，使得该解能在推理时间胜率 W^T 和与基础策略的 KL 散度之间实现良好甚至最佳的权衡。
标准胜率（无推理时间流程）。当不使用推理时间流程时（即 T 是恒等映射），W^T 会约简为标准胜率。将 Φ 设置为恒等变换能得到最佳的胜率与 KL 权衡曲线，注意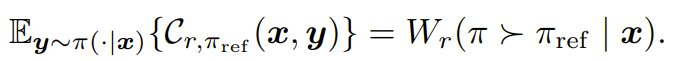 
该团队考虑了一系列仅依赖于输出的已校准奖励的推理时间流程，这被称为已校准流程（calibrated procedures）。然后他们探讨了如何为这一系列变换设计合适的 Φ。下面先定义已校准流程。
接下来的结果表明，对于已校准推理时间流程，求解 (13) 式的已对齐策略的胜率和 KL 散度独立于基础策略和奖励函数。
基于上述定理，便可以通过关注易于计算和模拟的简单连续语言模型来对变换 Φ 进行评估。下面，该团队使用了两个常用的推理时间流程 best-of-N 和 worst-of-N 为示例，展示了该定理可以如何有效地评估不同 Φ 函数的推理时间胜率与 KL 散度权衡曲线，这可用于在实际场景中找到合适的变换 Φ。
为 BoN 和 WoN 寻找更好的变换
这一节将主要关注以下两种推理时间流程：
-
best-of-N 推理时间流程 (BoN) -
worst-of-N 推理时间流程 (WoN)
定理 3 描述了 BoN 和 WoN 的性质。
通过调整式 (13) 中的 β，可以得到一条对齐曲线，该曲线绘制了不同对齐策略的推理时间胜率和 KL 散度偏差。这样，便能比较不同变换函数 Φ 的性能。
该团队还研究了不同的变换类型，并分析性地计算了使用定理 3 时通过调整 β 而得到的对齐曲线，即不同 β 下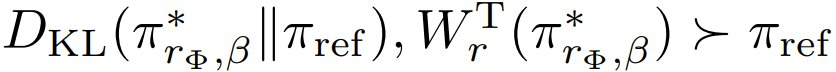 
的图。具体涉及的变换包括标准胜率的最优变换、指数函数和基于优化的变换。对这些变换的详细描述请参阅原论文。结果则见图 1。
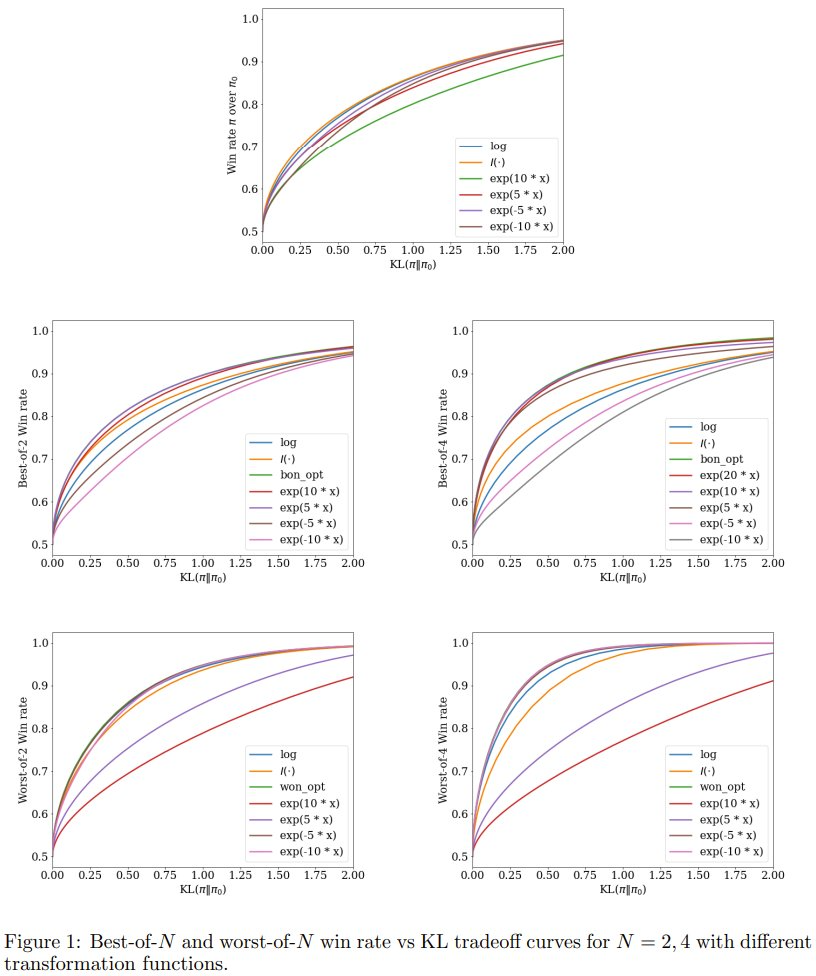
以上结果证明了在执行对齐时考虑推理时间过程的重要性。
该团队发现具有不同 t 的指数变换适用于不同的推理时间流程，这将是该团队在实验中的重点。接下来，该团队将研究在理想化的连续语言模型上找到的好变换是否可以泛化用于现实世界场景。
但在继续进行实验之前，还必需一种实用的算法来解决推理时间 KL-RL 优化问题。
CTRL：校准和变换式强化学习
该团队还提出了 Calibrate-and-Transform Reinforcement Learning（CTRL），即校准和变换式强化学习。这是一种用于推理时间胜率优化问题的求解器。
回想一下，新提出的解决方案可以分成三个阶段：奖励校准、奖励变换、标准的 KL-RL 求解器。前面已经重点介绍了奖励变换，下面将关注近似经验校准。再将其与奖励变换相结合，可得到最终的 CTRL 算法，见算法 1。
经验校准是这样的，首先对于强化学习训练数据中的每个提示词 x，从参照模型 π_ref 采样 K 个样本 z_1, z_2, …, z_K。然后将所有响应的奖励 {r (x, z_1), r (x, z_2), …r (x, z_K)} 排序，然后将 RLHF 训练期间提示词与响应对 (x, y) 的经验式已校准奖励分数配置为：
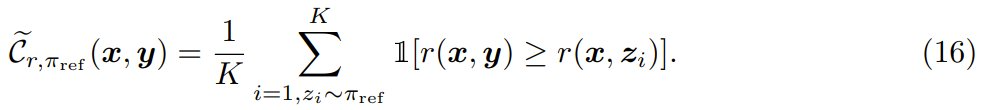
理想情况下，当 K → ∞ 时，经验的已校准奖励将收敛到真正的已校准奖励，并且可以通过 PPO 用于强化学习训练目标。但是，其成本可能很高，因为精确计算这个已校准奖励需要在 KL-RL 求解器中对每个提示词和每个 roll-out 进行采样并存储 K 个奖励分数。
于是，该团队提出了一种更为实用的方法，即通过在对数域中使用逐步函数来扩展校准曲线，进而近似求取该曲线。具体做法是，选取 p 个锚点 q_1, q_2, …，其中在每个分位数 q_i ∈ (0, 1) 处都取得零校准误差。算法 2 给出了简单情况（p = 1，中位数）的算法。更复杂的情况请访问原论文算法 3。
实验结果
这里略过具体的实验配置和过程，仅关注实验结果。
奖励模型通常没有正确校准
该团队首先测量了在 Anthropic helpfulness preference 数据集上训练的奖励模型的校准错误情况，具体做法是计算训练分割的数据中 10 个随机提示词的 100 个参照 – 策略响应的分数。
然后，该团队对这些分数进行排序，计算每个响应对应的排名，并将这些值绘制为散点图，如图 2（左）所示。如果模型经过完美校准，则每个提示词的点都将位于 y = x 线上。但是，请注意，对于大多数提示词，散点图与 y = x 线有显著偏差，并且这种偏差的程度因提示词而异。
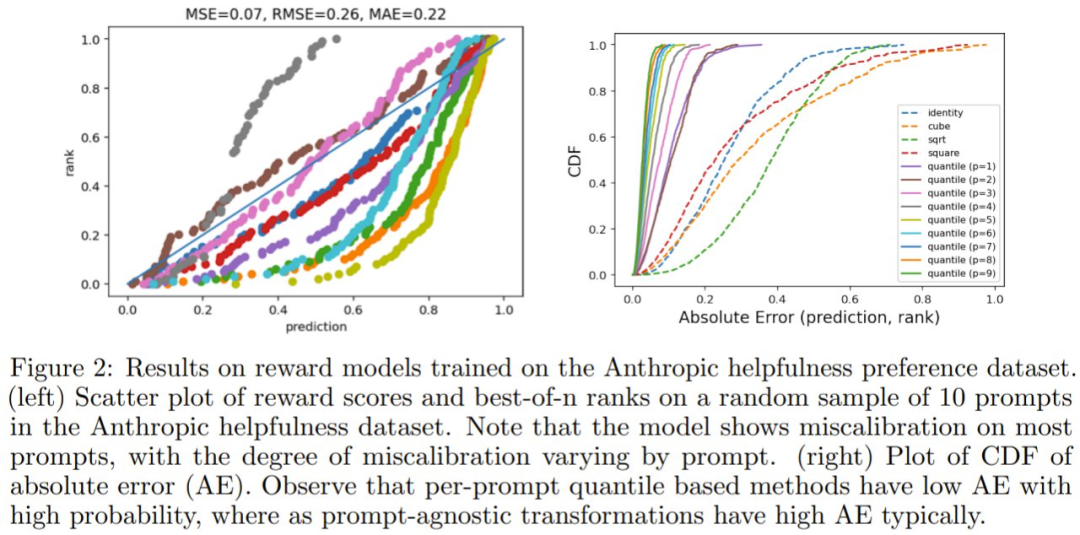
然后，该团队测量了奖励分数与其对应排名之间的绝对误差（AE），并在图 2（右）中绘制各种校准近似的 AE 的累积分布函数（CDF）。如果模型经过良好校准，则 AE 始终为零，因此 CDF 在零 AE 时达到一。
该团队发现奖励分数（identity）没有校准（平均 AE：0.22），并且使用固定奖励多项式变换函数（如平方根、立方、平方）不会降低校准误差（平均 AE > 0.15）。但是，使用基于分位数的奖励校准（quantile）可显著降低校准误差（平均 AE：0.02）。
已校准奖励可提升标准胜率
从图 3 的结果可以看到，相比于 IPO 和 BoNBoN，已校准奖励优化可以实现更好的胜率 – KL 权衡。
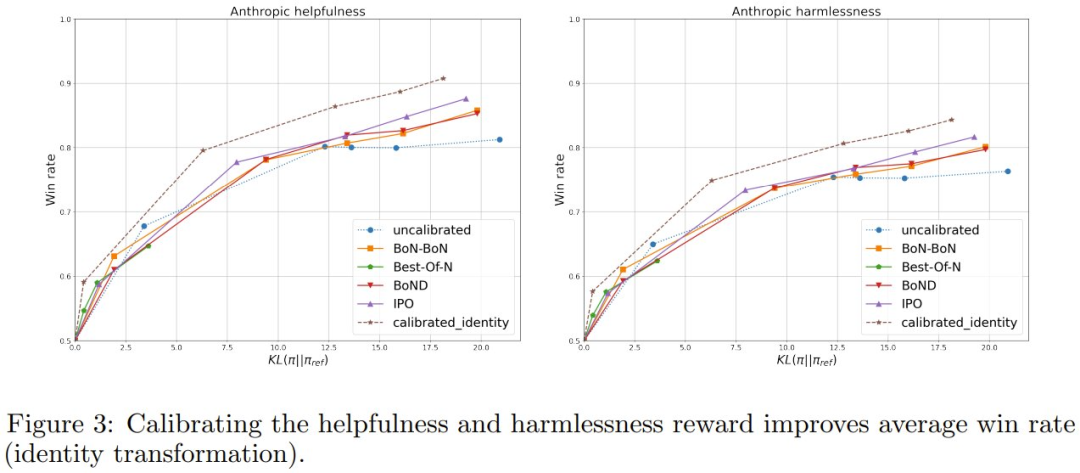
该团队将此增益归因于使用来自基础模型的 m 个样本能更高效地计算训练数据的胜率，而不是依赖 KL-RL 期间现有的成对比较数据。
CTRL 可提升 BoN
对于 Anthropic 对话数据集中的有用性目标，该团队的目标是通过已校准奖励的指数变换来优化已对齐模型的 Best-of-N 性能。
该团队测量了相对于基础策略模型的 Best-of-N（N =4）的胜率，见图 4。
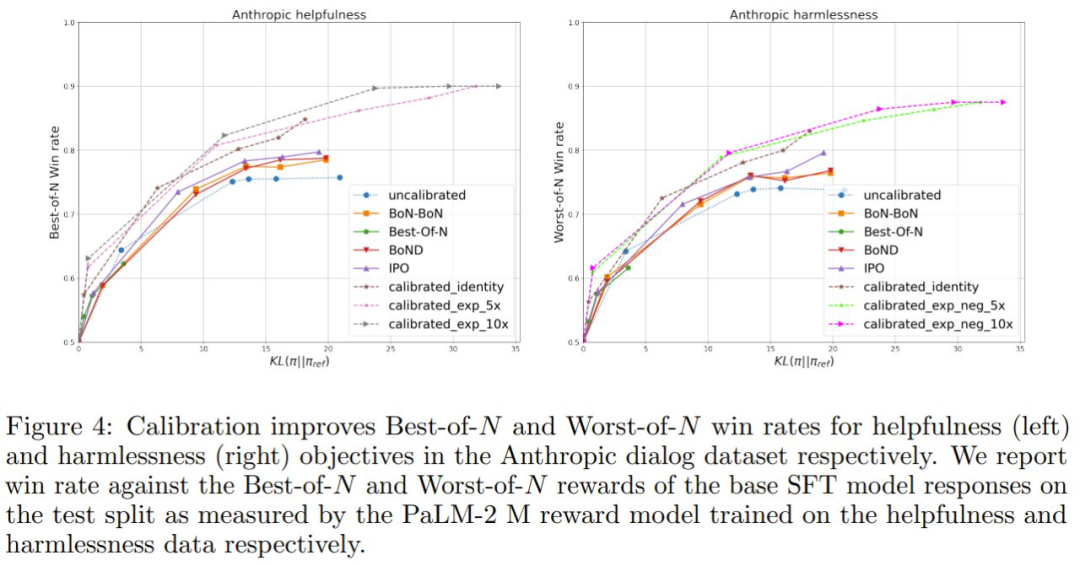
可以看到，与未在有用性目标上校准的模型相比，基于每个提示词的中位数奖励的校准实现了高 8-12% 的 Best-of-N 胜率。已校准奖励的指数变换优于其他。该团队发现，指数因子 t = 10 的效果最佳。此外，该团队表明 N 值不同时，也存在这些增益。
CTRL 可提升 WoN（BoN 越狱）
对于 Anthropic 对话数据集中的无害性目标，该团队的目标是提高已对齐策略模型的最差 Worst-of-N 性能，以提高面对对抗攻击的安全性。
在这里，该团队使用负指数变换 t < 0。从图 4 可以看到，与未校准的模型相比，基于每个提示词的中位数奖励的校准实现了高 4-9% 的 Worst-of-N 胜率。已校准奖励的负变换优于其它，其中 t = −10 表现最佳。
©
（文：机器之心）