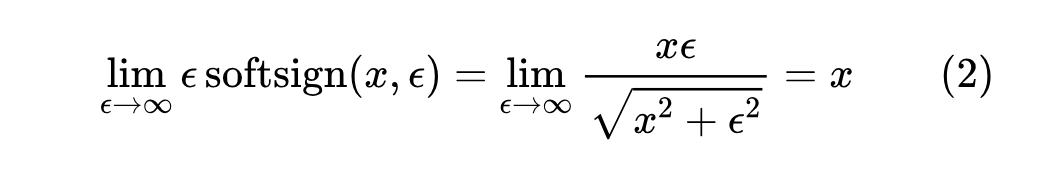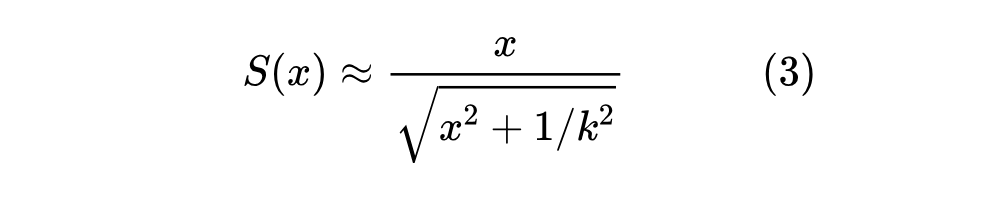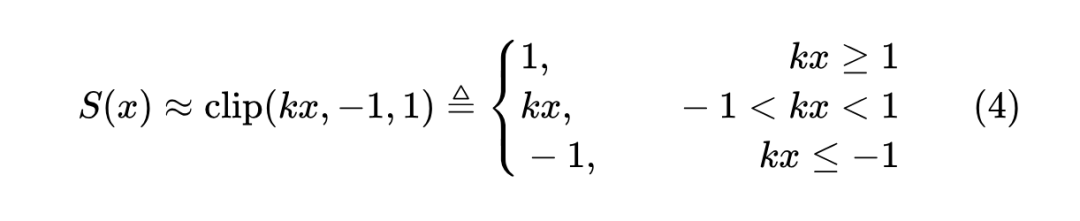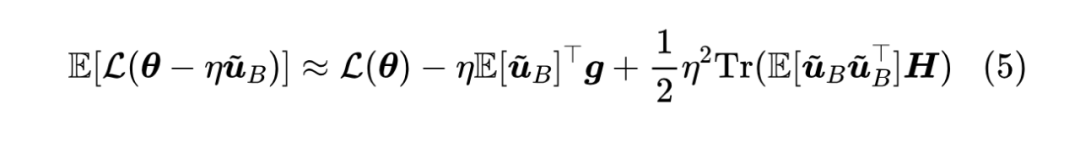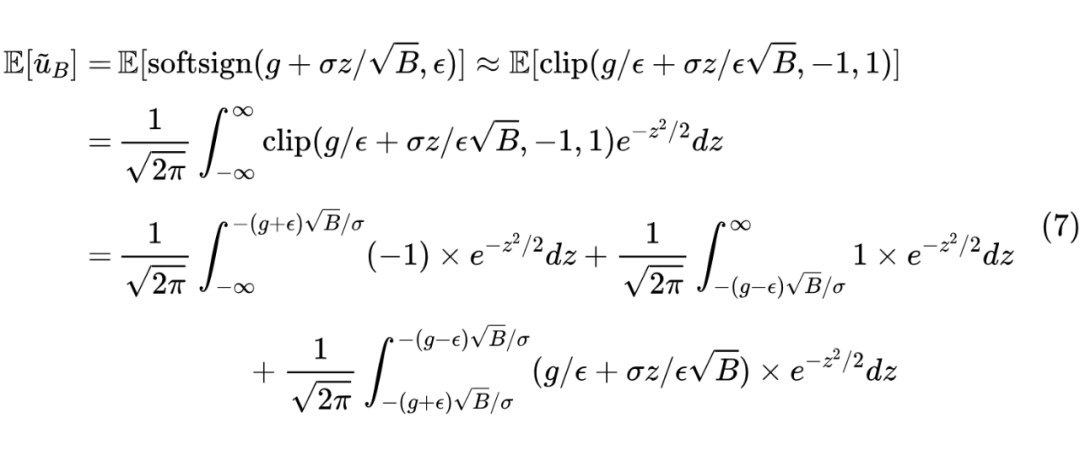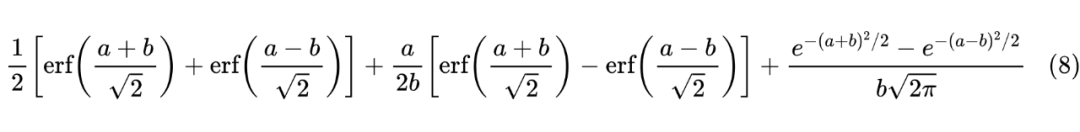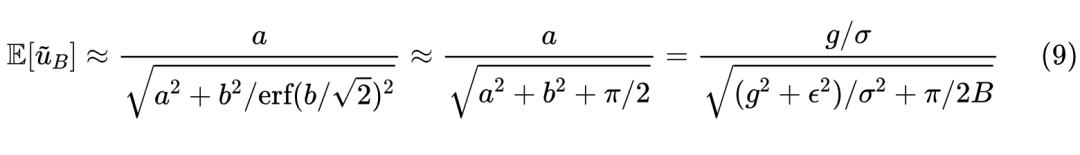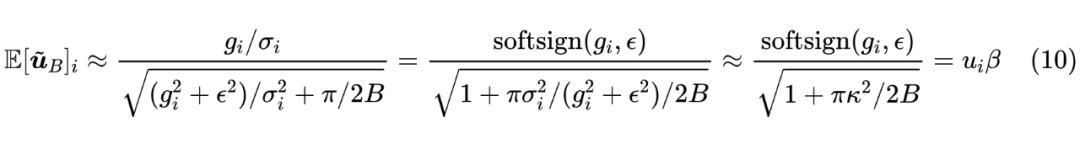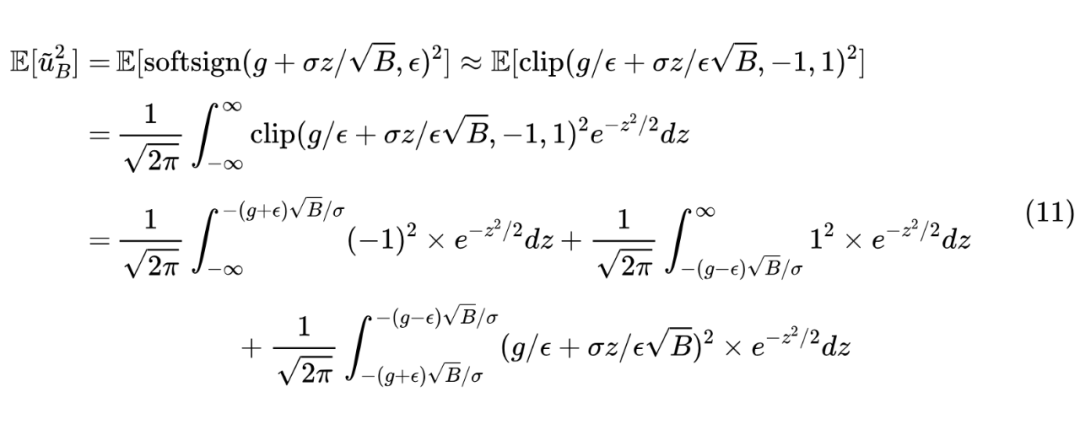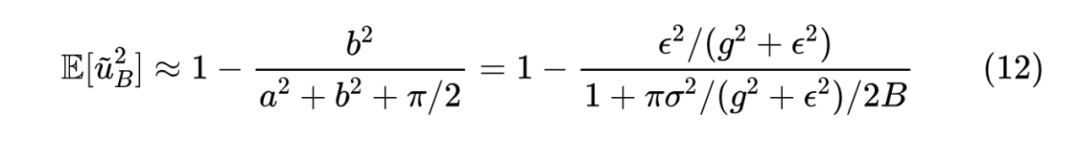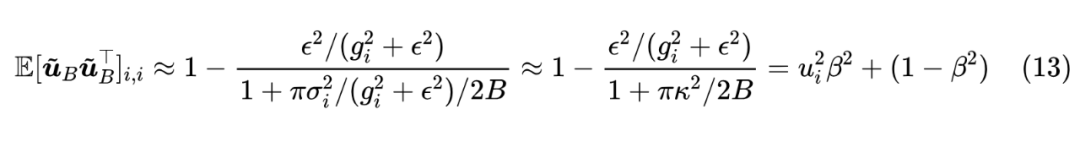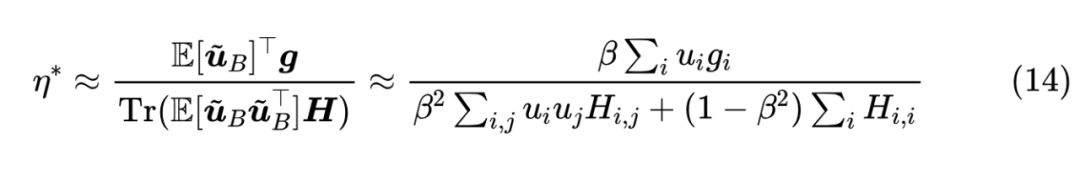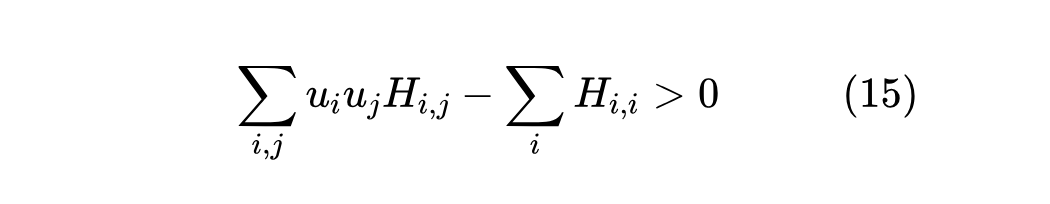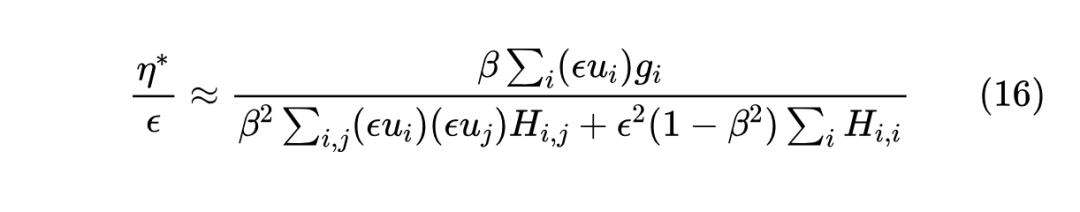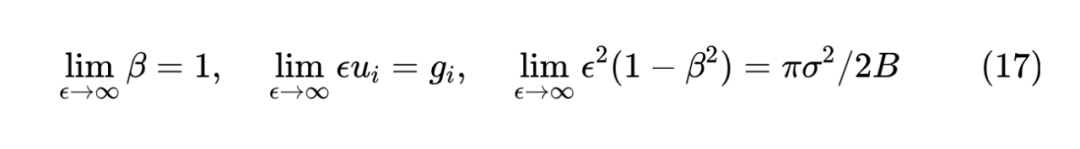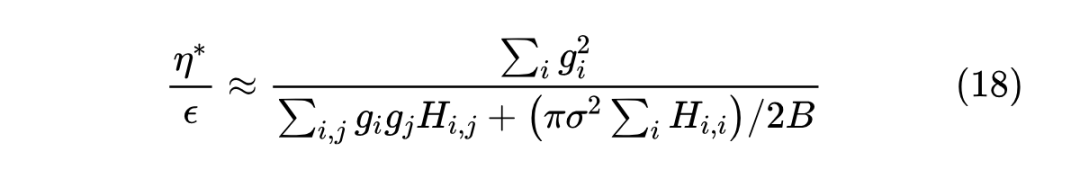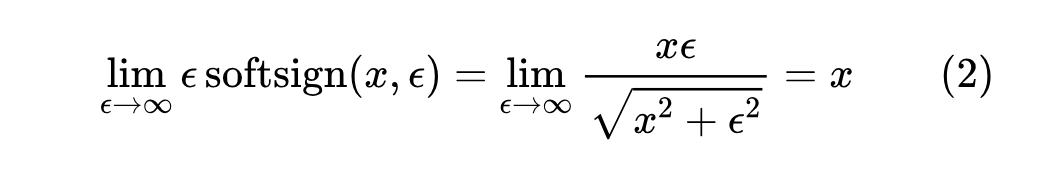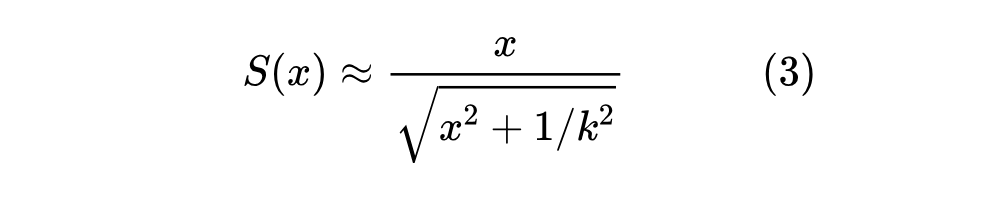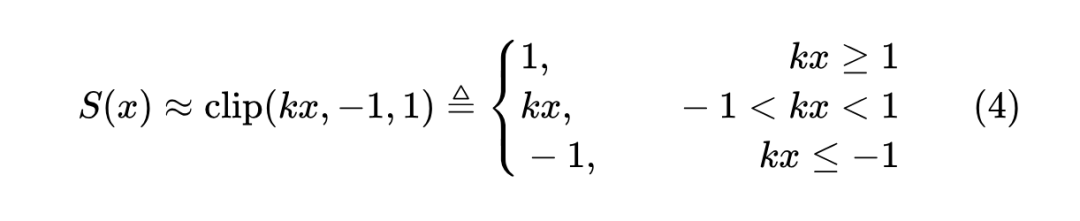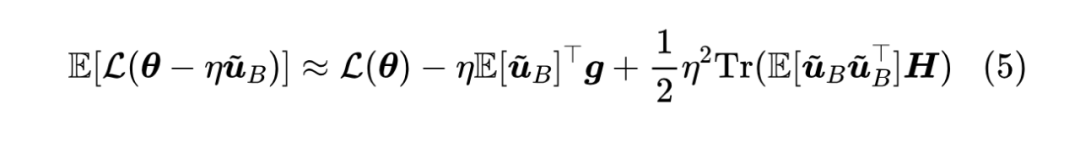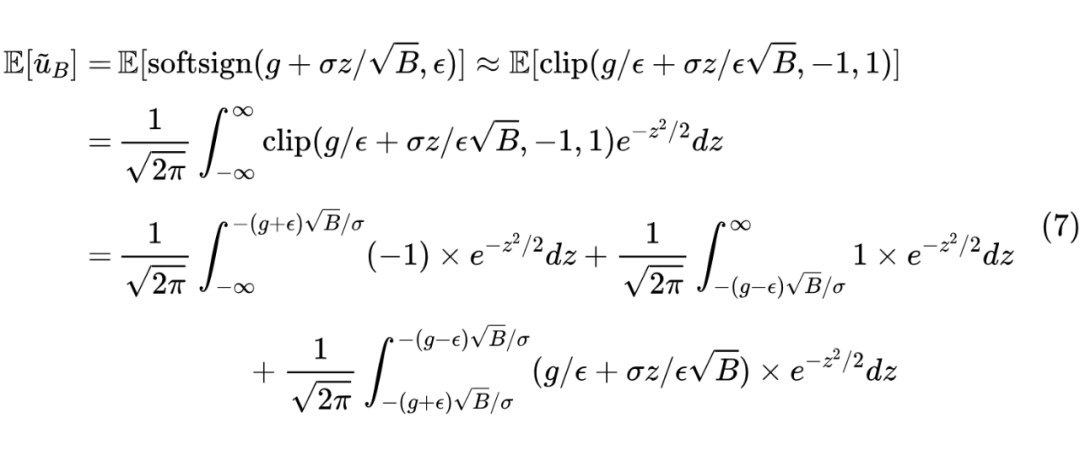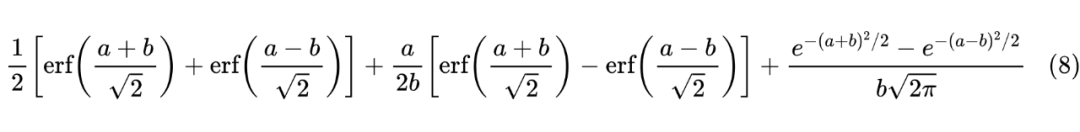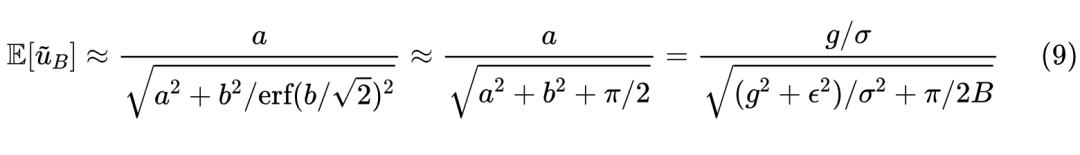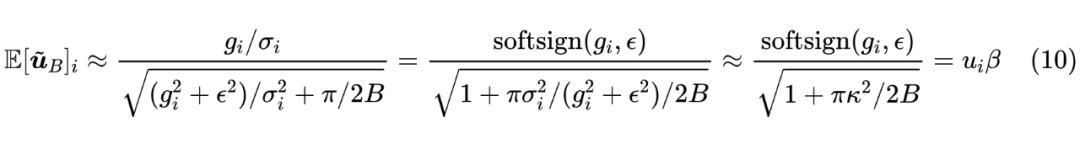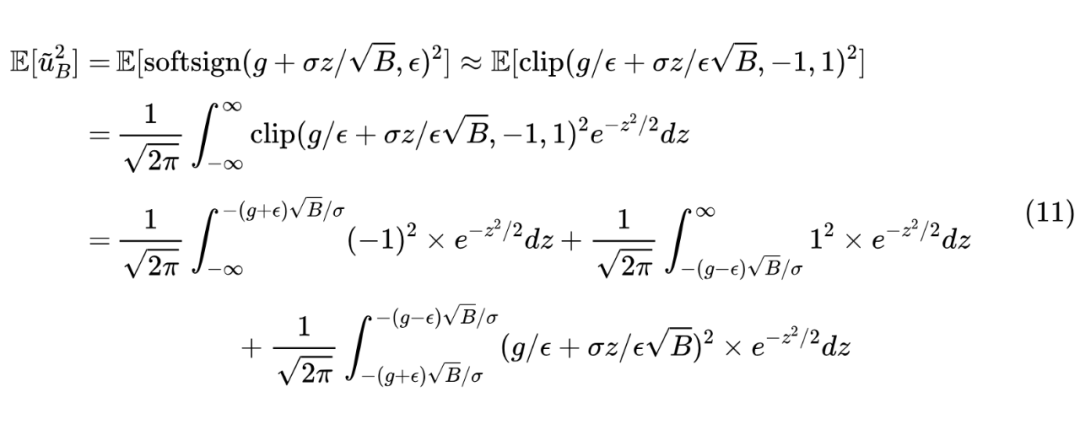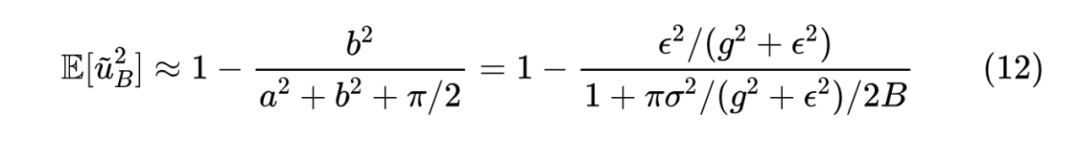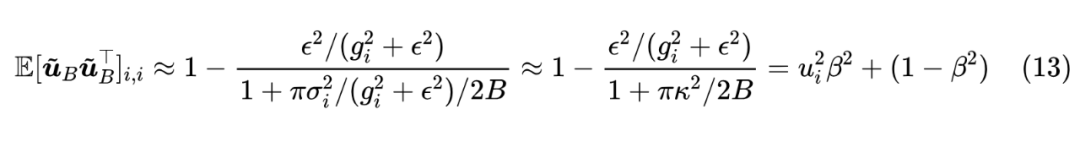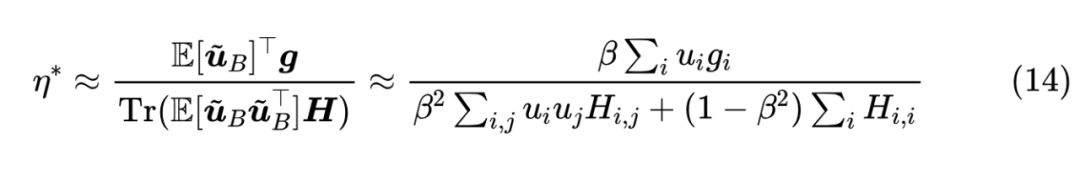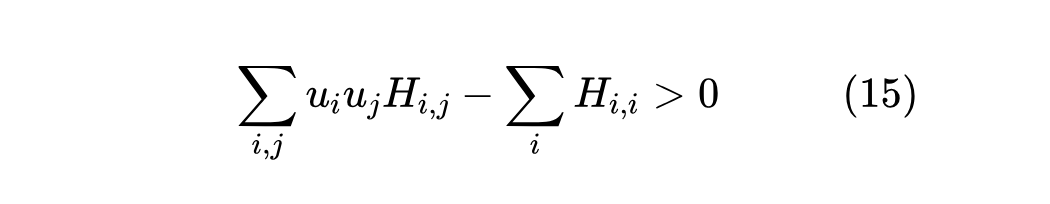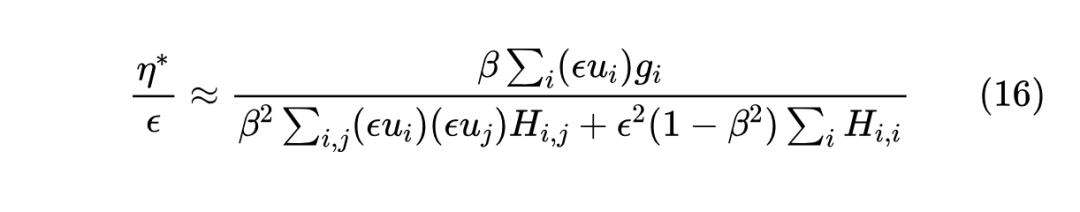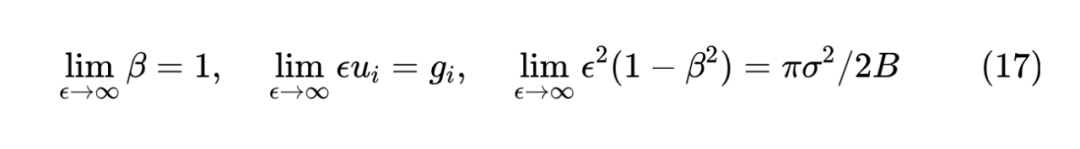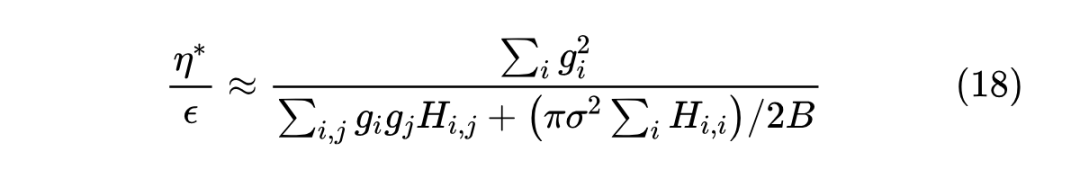Adam的epsilon如何影响学习率的Scaling Law？

作者
©PaperWeekly 原创 · 作者 | 苏剑林
单位 | 科学空间
研究方向 | NLP、神经网络
 
上一篇文章《当Batch Size增大时，学习率该如何随之变化？》我们从多个角度讨论了学习率与 Batch Size 之间的缩放规律，其中对于 Adam 优化器我们采用了 SignSGD 近似，这是分析 Adam 优化器常用的手段。那么一个很自然的问题就是：用 SignSGD 来近似 Adam 究竟有多科学呢？
我们知道，Adam 优化器的更新量分母会带有一个 ，初衷是预防除零错误，所以其值通常很接近于零，以至于我们做理论分析的时候通常选择忽略掉它。然而，当前 LLM 的训练尤其是低精度训练，我们往往会选择偏大的 ，这导致在训练的中、后期 往往已经超过梯度平方大小，所以 的存在事实上已经不可忽略。
因此，这篇文章我们试图探索 如何影响 Adam 的学习率与 Batch Size 的 Scaling Law，为相关问题提供一个参考的计算方案。

SoftSign

由于是接着上一篇文章介绍，所以就不再重复相关背景了。为了探究 的作用，我们从 SignSGD 换到 SoftSignSGD，即   变成 ，其中：

这个形式无疑更贴近更贴近 Adam。但在此之前，我们需要确认 是否真的不可忽略，才能确定是否有进一步研究的价值。
在 Keras 的 Adam 实现中， 的默认值是 ，在 Torch 中则是 ，这说明 的默认值是 级别，这时候梯度绝对值小于 几率还不算大；但在 LLM 中， 的普遍取值是 （比如 LLAMA2 [1]），这时候 的取值已经来到 级别，大概训练进入“正轨”后，梯度绝对值几乎普遍都小于 了，所以 的影响是显著的。
这个跟 LLM 的参数量也有一定关系。一个能稳定训练的模型，不管参数量多大，它的梯度模长大小大致都在同一数量级，这是反向传播的稳定性决定的（参考训练 1000 层的 Transformer 究竟有什么困难？）。因此，参数量越大的模型，平均下来每个参数的梯度绝度值就相对变小了，从而 的作用就更突出了。
值得指出的是， 的引入实际上提供了 Adam 与 SGD 之间的一个插值，这是因为当 时：
所以， 越大，Adam 表现越接近 SGD。
（注：本文 SoftSign 的概念，源于笔者跟 MSR 的刘力源老师、董城昱同学的一个 ongoing collaboration，经我们商量一致后先把这部分结果分享出来，更多后续结论敬请持续关注。）

S型近似

确认了引入 必要性后，我们着手开始分析。在分析过程中，我们将会反复遇到 S 型函数，所以还有一个准备工作是探究 S 型函数的简单近似。
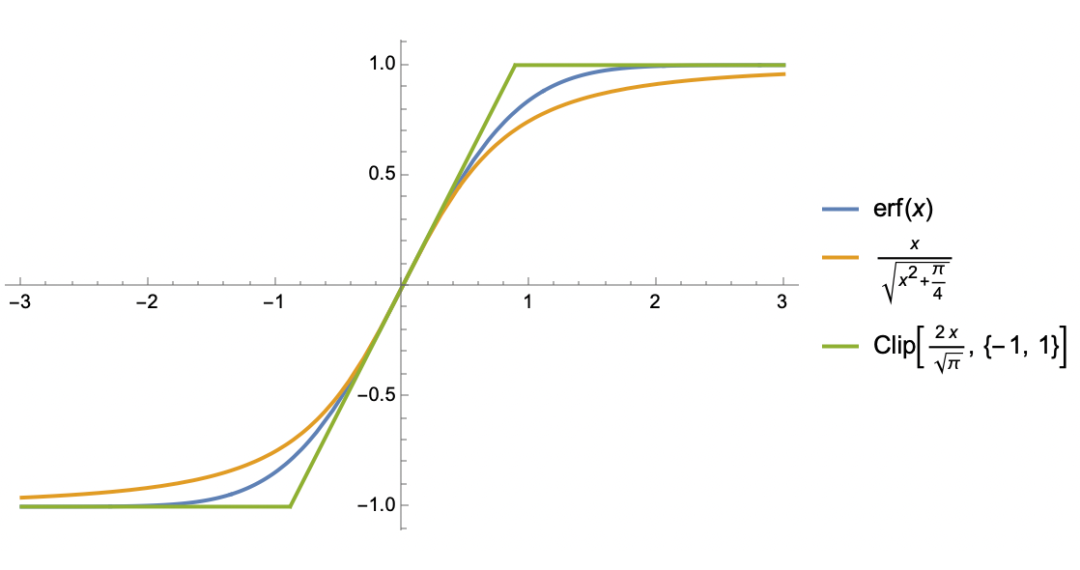
S 型函数相比大家已经见怪不怪，上一节引入的 函数本身就是之一，上一篇文章分析过程中的 函数也是一例，此外还有 、 等。接下来我们处理的是满足如下特性的 S 型函数 ：
1. 全局光滑且单调递增；
2. 奇函数，值域是 [-1,1]；
3. 在原点处斜率为 。
对于这类函数，我们考虑两种近似。第一种近似跟 类似：

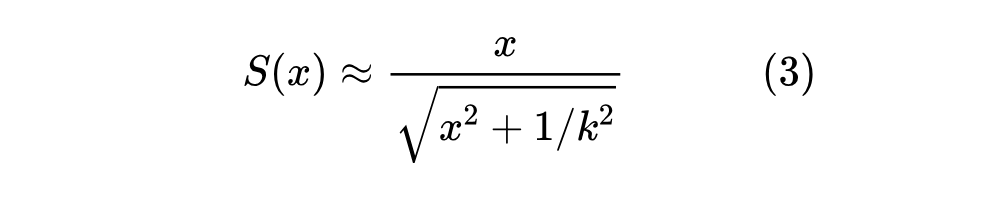
它大概是保留 如上 3 点性质的最简单函数了；第二种近似是基于 函数：
这本质上是一个分段线性函数，放弃了全局光滑的性质，但分段线性会使得积分算起来更容易，我们很快就会看到这一点。

▲ Erf 函数与它的两种近似

均值估计

事不宜迟，沿着上一篇文章的方法，出发点还是：

我们需要做的事情就是估计 和 。
这一节我们算的是 ，为此我们需要用 函数去近似 函数：
然后我们有：
积分形式很复杂，但用 Mathematica 算并不难，结果可以用 函数表达出来：

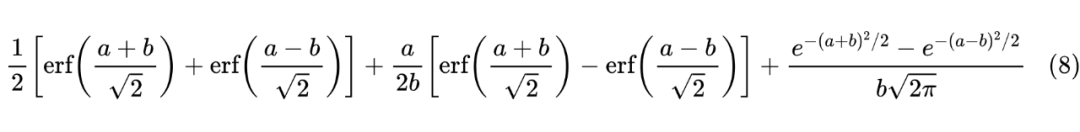
其中 。这个函数看起来比较复杂，但它刚好是 的 S 型函数，值域为 且在 处的斜率是 ，所以利用第一种近似形式
第二个约等号是利用近似 来处理分母中的 。可以说相当幸运，最终的形式并没有太复杂。接着我们有：

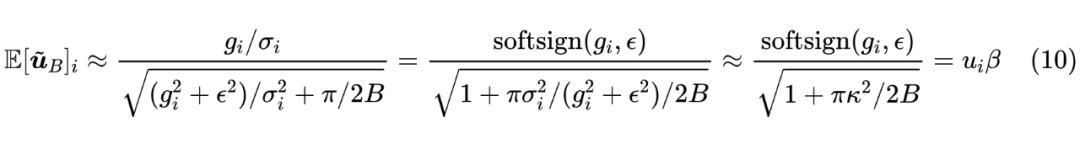
跟上一篇文章一样，最后一个约等号使用了平均场近似， 是全体 的某种平均，而 以及 。

方差估计

均值也就是一阶矩解决了，现在轮到二阶矩了：
结果同样可以用 函数表示，但更加冗长，这里就不写出来了，还是那句话，对 Mathematica 来说这都不是事。视为 的函数时，可以发现结果是一条倒钟形的曲线，关于 轴对称，上界是 1，最小值是则在 内。
参考 的近似式（9），我们选择如下近似：
有一说一，这个近似的精度并不高，主要是为了计算的方便，但它已经保留了倒钟形、 轴对称、上界为 1、 时结果为 1、 结果则为 0 等关键特性。接下来继续应用平均场近似：

 

所以 。其中 这一项就代表了 的协方差矩阵 ，它是一个对角阵，这是可以预料的，因为我们的假设之一是 各分量之间的独立性，所以协方差矩阵必然是对角阵。

结果初探

由此我们得到：
注意，除了 外，剩余的其他符号都不依赖于 ，所以上式已经给出 与 的依赖关系。注意为了保证极小值的存在性，我们都会假设 矩阵的正定性，而在此假设之下必然有 和 。
上一篇文章我们说 Adam 最重要的特性是可能会出现 “Surge 现象”，即 关于 不再是全局的单调递增函数。接下来我们将会证明， 的引入会降低 现象出现的几率，并且 时完全消失。这个证明并不难，很明显 Surge 现象出现的必要条件是：

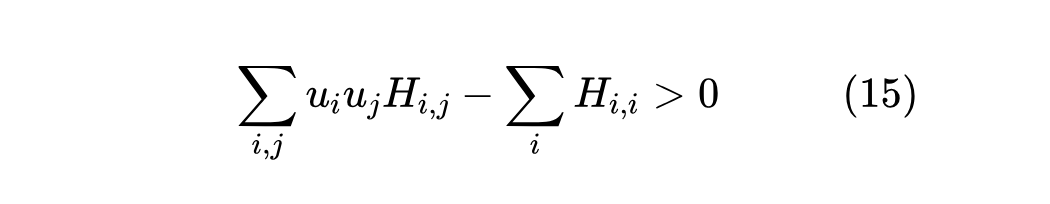
若否，整个 关于 便是单调递增的，而 关于 是单调递增的，所以整个 关于 单调递增，不存在 Surge 现象。
别忘了 是关于 的单调递减函数，所以当 增大时 会更小，从而上述不等式成立的可能性更低，并且 时 为零，上述不等式不可能再成立，因此 Surge 现象消失。
进一步，我们可以证明 时，结果跟 SGD 的一致，这只需要留意到：
我们有极限：
这里 是全体 的某种平均。于是我们得到当 足够大时有近似：
右端就是假设梯度协方差矩阵为 ( 时的 SGD 结果。

文章小结
本文延续了上一篇文章的方法，尝试分析了 Adam 的 对学习率与 Batch Size 之间的 Scaling Law 的影响，结果是一个介乎 SGD 与 SignSGD 之间的形式，当 越大，结果越接近 SGD，“Surge 现象”出现的概率就越低。总的来说，计算结果没有特别让人意外之处，但可以作为分析 作用的一个参考过程。

（文：PaperWeekly）

欢迎分享

发表评论