博客来源:https://leimao.github.io/blog/CUDA-Shared-Memory-Swizzling/ ,来自Lei Mao,已获得作者转载授权。后续会转载一些Lei Mao的CUDA相关Blog,也是一个完整的专栏,Blog会从稍早一些的CUDA架构到当前最新的CUDA架构,也会包含实用工程技巧,底层指令分析,Cutlass分析等等多个课题,是一个时间线十分明确的专栏。
CUDA 共享内存 Swizzling 技术
介绍
当我们编写使用共享内存的CUDAkernel 时,必须小心共享内存bank冲突(https://leimao.github.io/blog/CUDA-Shared-Memory-Bank/)。严重的共享内存bank冲突会带来显著的性能损失。
处理共享内存bank冲突的一种简单方法是使用填充(padding)。然而,填充会浪费共享内存并可能产生其他缺陷。
在这篇博客中,我想讨论如何使用swizzling技术来处理共享内存bank冲突。Swizzling是一种更复杂的技术,可以在不浪费共享内存的情况下避免共享内存bank冲突。
CUDA 共享内存 Swizzling
Swizzling 示例
当我们使用CUDA共享内存缓存数据而不使用填充时,warp对共享内存的读取或写入操作很常见会导致共享内存bank冲突。Swizzling是一种重新排列共享内存索引映射的技术,用于避免共享内存bank冲突。矩阵转置是一个完美的例子,如果实现不使用填充或swizzling,就会产生共享内存bank冲突。
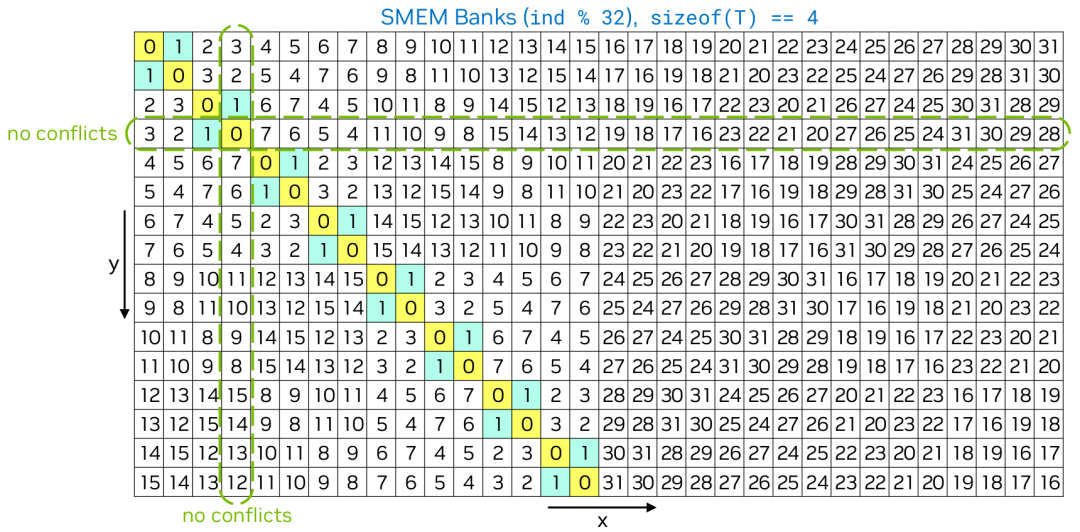
在上面的示例中,共享内存是一个大小为 的二维 float 数组。在矩阵转置的情况下,每个warp从全局内存读取一行32个值,并使用swizzling将它们写入共享内存。写入共享内存时不会产生共享内存bank冲突。为了执行矩阵转置,每个warp从共享内存读取两个经过swizzling的”列”的32个值,并将它们写入全局内存。例如,swizzling后的第0列和第1列分别用黄色和青色标记。这样,从共享内存读取时只会产生一个共享内存bank冲突。如果不使用swizzling,从共享内存读取时会产生16个(2路)共享内存bank冲突。当然,显然,如果共享内存是大小为 的二维 float 数组,那么写入和读取共享内存时都不会产生共享内存bank冲突。
Swizzling 公式
给定共享内存上的数组 T array[][NX],我们定义 。 的允许值是大于或等于32的2的幂,如32、64、128、256等。
给定 T array[][NX] 中的索引 [y][x],我们可以按如下方式计算swizzling后的索引 :
-
计算 字节段内 字节块的索引:
i_chunk = (y × NX + x) × sizeof(T) / sizeof(TC)
y_chunk = i / (SWIZZLE_SIZE / sizeof(TC))
x_chunk = i % (SWIZZLE_SIZE / sizeof(TC))
-
使用 运算计算 字节块的swizzling索引:
x_chunk_swz = y_chunk ^ x_chunk -
计算swizzling索引:
x_swz = x_chunk_swz × sizeof(TC) / sizeof(T) % NX + x % (sizeof(TC) / sizeof(T))
Swizzling 属性
这个swizzling公式具有以下属性:
-
swizzling前后的索引必须是一对一映射的。 -
NX必须是2的幂。 -
给定任意 和任意 ,唯一swizzling索引 的数量应该最大化。
属性1确保swizzling过程中不会有数据丢失。属性2确保swizzling前后的索引是一对一映射的。
这里我将展示从swizzling公式得出的属性的一些非正式数学证明。
证明
我们首先证明属性1。
看起来我们为 推导出了另一个等价公式。注意当 是2的幂时, 是一个位右移操作。
看起来我们也为 推导出了另一个等价公式。
注意 是按位异或运算。如果 或 中的任一个是常数,映射就是一对一映射。
这里的证明变得有点非正式。
因为连续的 个 值将映射到一个唯一的trunk索引 , 和 之间的映射是一对一映射,一个 值将映射到一个唯一的 值。为了创建swizzling索引 和原始索引 之间的一对一映射,添加了偏移量 。因此,swizzling前后的索引必须是一对一映射的。
属性2很容易证明。
给定以下 的表达式,属性3可能更容易理解。
给定任意 和任意 ,唯一swizzling索引 的数量是NX,这是最大化的。
示例
矩阵转置
在这个示例中,我们用三种不同的方式实现了使用共享内存的矩阵转置CUDAkernel :
-
有共享内存bank冲突的转置。 -
通过填充避免共享内存bank冲突的转置。 -
通过swizzling避免共享内存bank冲突的转置。
#include <algorithm>
#include <cassert>
#include <chrono>
#include <cstdio>
#include <functional>
#include <iomanip>
#include <iostream>
#include <random>
#include <vector>
#include <cuda_runtime.h>
// CUDA错误检查宏
#define CHECK_CUDA_ERROR(val) check((val), #val, __FILE__, __LINE__)
void check(cudaError_t err, char const* func, char const* file, int line)
{
if (err != cudaSuccess)
{
std::cerr << "CUDA Runtime Error at: " << file << ":" << line
<< std::endl;
std::cerr << cudaGetErrorString(err) << " " << func << std::endl;
std::exit(EXIT_FAILURE);
}
}
// 检查最后的CUDA错误
#define CHECK_LAST_CUDA_ERROR() check_last(__FILE__, __LINE__)
void check_last(char const* file, int line)
{
cudaError_t const err{cudaGetLastError()};
if (err != cudaSuccess)
{
std::cerr << "CUDA Runtime Error at: " << file << ":" << line
<< std::endl;
std::cerr << cudaGetErrorString(err) << std::endl;
std::exit(EXIT_FAILURE);
}
}
// 性能测量函数模板
template <class T>
float measure_performance(std::function<T(cudaStream_t)> bound_function,
cudaStream_t stream, size_t num_repeats = 10,
size_t num_warmups = 10)
{
cudaEvent_t start, stop;
float time;
CHECK_CUDA_ERROR(cudaEventCreate(&start));
CHECK_CUDA_ERROR(cudaEventCreate(&stop));
// 预热运行
for (size_t i{0}; i < num_warmups; ++i)
{
bound_function(stream);
}
CHECK_CUDA_ERROR(cudaStreamSynchronize(stream));
// 性能测量
CHECK_CUDA_ERROR(cudaEventRecord(start, stream));
for (size_t i{0}; i < num_repeats; ++i)
{
bound_function(stream);
}
CHECK_CUDA_ERROR(cudaEventRecord(stop, stream));
CHECK_CUDA_ERROR(cudaEventSynchronize(stop));
CHECK_LAST_CUDA_ERROR();
CHECK_CUDA_ERROR(cudaEventElapsedTime(&time, start, stop));
CHECK_CUDA_ERROR(cudaEventDestroy(start));
CHECK_CUDA_ERROR(cudaEventDestroy(stop));
floatconst latency{time / num_repeats};
return latency;
}
// 向上取整除法
constexpr size_t div_up(size_t a, size_t b) { return (a + b - 1) / b; }
// 矩阵转置kernel (带有填充选项以避免bank冲突)
template <typename T, size_t BLOCK_TILE_SIZE_X = 32,
size_t BLOCK_TILE_SIZE_Y = 32, size_t BLOCK_TILE_SKEW_SIZE_X = 0>
__global__ void transpose(T* output_matrix, T const* input_matrix, size_t M,
size_t N)
{
// 如果BLOCK_TILE_SKEW_SIZE_X != 0,浪费一些共享内存来避免bank冲突
__shared__ T
shm[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_X + BLOCK_TILE_SKEW_SIZE_X];
// 在某些算法中,比如矩阵乘法,
// 一个warp的线程必须访问共享内存中2D矩阵的一列。
// 使用传统的索引映射,如果列大小不是warp大小的倍数,就会产生bank冲突。
size_tconst input_matrix_from_idx_x{threadIdx.x + blockIdx.x * blockDim.x};
size_tconst input_matrix_from_idx_y{threadIdx.y + blockIdx.y * blockDim.y};
size_tconst input_matrix_from_idx{input_matrix_from_idx_x +
input_matrix_from_idx_y * N};
size_tconst shm_to_idx_x{threadIdx.x};
size_tconst shm_to_idx_y{threadIdx.y};
if ((input_matrix_from_idx_y < M) && (input_matrix_from_idx_x < N))
{
// 合并的全局内存访问
// 无共享内存bank冲突
shm[shm_to_idx_y][shm_to_idx_x] = input_matrix[input_matrix_from_idx];
}
// 确保块内的缓冲区被填满
__syncthreads();
// 计算读取共享内存时的索引
size_tconst block_thread_idx{threadIdx.x + threadIdx.y * blockDim.x};
size_tconst shm_from_idx_x{block_thread_idx / BLOCK_TILE_SIZE_Y};
size_tconst shm_from_idx_y{block_thread_idx % BLOCK_TILE_SIZE_Y};
size_tconst output_matrix_to_idx_x{shm_from_idx_y +
blockIdx.y * blockDim.y};
size_tconst output_matrix_to_idx_y{shm_from_idx_x +
blockIdx.x * blockDim.x};
size_tconst output_matrix_to_idx{output_matrix_to_idx_x +
output_matrix_to_idx_y * M};
if ((output_matrix_to_idx_y < N) && (output_matrix_to_idx_x < M))
{
// 合并的全局内存访问
// 如果BLOCK_TILE_SKEW_SIZE_X = 1,则无共享内存bank冲突
output_matrix[output_matrix_to_idx] =
shm[shm_from_idx_y][shm_from_idx_x];
}
}
// 使用swizzling技术的矩阵转置kernel
template <typename T, size_t BLOCK_TILE_SIZE_X = 32,
size_t BLOCK_TILE_SIZE_Y = 32>
__global__ void transpose_swizzling(T* output_matrix, T const* input_matrix,
size_t M, size_t N)
{
__shared__ T shm[BLOCK_TILE_SIZE_Y][BLOCK_TILE_SIZE_X];
// 在某些算法中,比如矩阵乘法,
// 一个warp的线程必须访问共享内存中2D矩阵的一列。
// 使用传统的索引映射,如果列大小不是warp大小的倍数,就会产生bank冲突。
size_tconst input_matrix_from_idx_x{threadIdx.x + blockIdx.x * blockDim.x};
size_tconst input_matrix_from_idx_y{threadIdx.y + blockIdx.y * blockDim.y};
size_tconst input_matrix_from_idx{input_matrix_from_idx_x +
input_matrix_from_idx_y * N};
size_tconst shm_to_idx_x{threadIdx.x};
size_tconst shm_to_idx_y{threadIdx.y};
// 使用XOR操作计算swizzling后的x索引
size_tconst shm_to_idx_x_swizzled{(shm_to_idx_x ^ shm_to_idx_y) %
BLOCK_TILE_SIZE_X};
if ((input_matrix_from_idx_y < M) && (input_matrix_from_idx_x < N))
{
// 合并的全局内存访问
// 无共享内存bank冲突
shm[shm_to_idx_y][shm_to_idx_x_swizzled] =
input_matrix[input_matrix_from_idx];
}
// 确保块内的缓冲区被填满
__syncthreads();
// 计算读取共享内存时的索引
size_tconst block_thread_idx{threadIdx.x + threadIdx.y * blockDim.x};
size_tconst shm_from_idx_x{block_thread_idx / BLOCK_TILE_SIZE_Y};
size_tconst shm_from_idx_y{block_thread_idx % BLOCK_TILE_SIZE_Y};
// 读取时也使用相同的swizzling索引
size_tconst shm_from_idx_x_swizzled{(shm_from_idx_x ^ shm_from_idx_y) %
BLOCK_TILE_SIZE_X};
size_tconst output_matrix_to_idx_x{shm_from_idx_y +
blockIdx.y * blockDim.y};
size_tconst output_matrix_to_idx_y{shm_from_idx_x +
blockIdx.x * blockDim.x};
size_tconst output_matrix_to_idx{output_matrix_to_idx_x +
output_matrix_to_idx_y * M};
if ((output_matrix_to_idx_y < N) && (output_matrix_to_idx_x < M))
{
// 合并的全局内存访问
// 无共享内存bank冲突
output_matrix[output_matrix_to_idx] =
shm[shm_from_idx_y][shm_from_idx_x_swizzled];
}
}
// 启动有共享内存bank冲突的转置kernel
template <typename T>
void launch_transpose_with_shm_bank_conflict(T* d_output_matrix,
T const* d_input_matrix, size_t M,
size_t N, cudaStream_t stream)
{
constexprsize_t BLOCK_TILE_SIZE_X{32};
constexprsize_t BLOCK_TILE_SIZE_Y{32};
constexprsize_t BLOCK_TILE_SKEW_SIZE_X{0}; // 不使用填充
dim3 const block_size{BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y};
dim3 const grid_size{static_cast<unsignedint>(div_up(N, block_size.x)),
static_cast<unsignedint>(div_up(M, block_size.y))};
transpose<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SKEW_SIZE_X>
<<<grid_size, block_size, 0, stream>>>(d_output_matrix, d_input_matrix,
M, N);
CHECK_LAST_CUDA_ERROR();
}
// 启动通过填充避免共享内存bank冲突的转置kernel
template <typename T>
void launch_transpose_without_shm_bank_conflict_via_padding(
T* d_output_matrix, T const* d_input_matrix, size_t M, size_t N,
cudaStream_t stream)
{
constexprsize_t BLOCK_TILE_SIZE_X{32};
constexprsize_t BLOCK_TILE_SIZE_Y{32};
constexprsize_t BLOCK_TILE_SKEW_SIZE_X{1}; // 使用1个元素的填充
dim3 const block_size{BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y};
dim3 const grid_size{static_cast<unsignedint>(div_up(N, block_size.x)),
static_cast<unsignedint>(div_up(M, block_size.y))};
transpose<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y, BLOCK_TILE_SKEW_SIZE_X>
<<<grid_size, block_size, 0, stream>>>(d_output_matrix, d_input_matrix,
M, N);
CHECK_LAST_CUDA_ERROR();
}
// 启动通过swizzling避免共享内存bank冲突的转置kernel
template <typename T>
void launch_transpose_without_shm_bank_conflict_via_swizzling(
T* d_output_matrix, T const* d_input_matrix, size_t M, size_t N,
cudaStream_t stream)
{
constexprsize_t BLOCK_TILE_SIZE_X{32};
constexprsize_t BLOCK_TILE_SIZE_Y{32};
dim3 const block_size{BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y};
dim3 const grid_size{static_cast<unsignedint>(div_up(N, block_size.x)),
static_cast<unsignedint>(div_up(M, block_size.y))};
transpose_swizzling<T, BLOCK_TILE_SIZE_X, BLOCK_TILE_SIZE_Y><<<grid_size, block_size, 0, stream>>>(
d_output_matrix, d_input_matrix, M, N);
CHECK_LAST_CUDA_ERROR();
}
// 比较两个数组是否相等
template <typename T>
bool is_equal(T const* data_1, T const* data_2, size_t size)
{
for (size_t i{0}; i < size; ++i)
{
if (data_1[i] != data_2[i])
{
returnfalse;
}
}
returntrue;
}
// 验证转置实现的正确性
template <typename T>
bool verify_transpose_implementation(
std::function<void(T*, T const*, size_t, size_t, cudaStream_t)>
transpose_function,
size_t M, size_t N)
{
// 固定随机种子以确保可重现性
std::mt19937 gen{0};
cudaStream_t stream;
size_tconst matrix_size{M * N};
std::vector<T> matrix(matrix_size, 0.0f);
std::vector<T> matrix_transposed(matrix_size, 1.0f);
std::vector<T> matrix_transposed_reference(matrix_size, 2.0f);
std::uniform_real_distribution<T> uniform_dist(-256, 256);
// 生成随机矩阵
for (size_t i{0}; i < matrix_size; ++i)
{
matrix[i] = uniform_dist(gen);
}
// 使用CPU创建参考转置矩阵
for (size_t i{0}; i < M; ++i)
{
for (size_t j{0}; j < N; ++j)
{
size_tconst from_idx{i * N + j};
size_tconst to_idx{j * M + i};
matrix_transposed_reference[to_idx] = matrix[from_idx];
}
}
// GPU内存分配和数据传输
T* d_matrix;
T* d_matrix_transposed;
CHECK_CUDA_ERROR(cudaMalloc(&d_matrix, matrix_size * sizeof(T)));
CHECK_CUDA_ERROR(cudaMalloc(&d_matrix_transposed, matrix_size * sizeof(T)));
CHECK_CUDA_ERROR(cudaStreamCreate(&stream));
CHECK_CUDA_ERROR(cudaMemcpy(d_matrix, matrix.data(),
matrix_size * sizeof(T),
cudaMemcpyHostToDevice));
// 执行转置
transpose_function(d_matrix_transposed, d_matrix, M, N, stream);
CHECK_CUDA_ERROR(cudaStreamSynchronize(stream));
CHECK_CUDA_ERROR(cudaMemcpy(matrix_transposed.data(), d_matrix_transposed,
matrix_size * sizeof(T),
cudaMemcpyDeviceToHost));
// 验证正确性
boolconst correctness{is_equal(matrix_transposed.data(),
matrix_transposed_reference.data(),
matrix_size)};
// 清理资源
CHECK_CUDA_ERROR(cudaFree(d_matrix));
CHECK_CUDA_ERROR(cudaFree(d_matrix_transposed));
CHECK_CUDA_ERROR(cudaStreamDestroy(stream));
return correctness;
}
// 性能测试函数
template <typename T>
float profile_transpose_implementation(
std::function<void(T*, T const*, size_t, size_t, cudaStream_t)>
transpose_function,
size_t M, size_t N)
{
constexprint num_repeats{100}; // 重复次数
constexprint num_warmups{10}; // 预热次数
cudaStream_t stream;
size_tconst matrix_size{M * N};
T* d_matrix;
T* d_matrix_transposed;
// GPU内存分配
CHECK_CUDA_ERROR(cudaMalloc(&d_matrix, matrix_size * sizeof(T)));
CHECK_CUDA_ERROR(cudaMalloc(&d_matrix_transposed, matrix_size * sizeof(T)));
CHECK_CUDA_ERROR(cudaStreamCreate(&stream));
// 绑定函数参数
std::function<void(cudaStream_t)> const transpose_function_wrapped{
std::bind(transpose_function, d_matrix_transposed, d_matrix, M, N,
std::placeholders::_1)};
// 测量性能
floatconst transpose_function_latency{measure_performance(
transpose_function_wrapped, stream, num_repeats, num_warmups)};
// 清理资源
CHECK_CUDA_ERROR(cudaFree(d_matrix));
CHECK_CUDA_ERROR(cudaFree(d_matrix_transposed));
CHECK_CUDA_ERROR(cudaStreamDestroy(stream));
return transpose_function_latency;
}
// 打印延迟信息
void print_latencty(std::string const& kernel_name, float latency)
{
std::cout << kernel_name << ": " << std::fixed << std::setprecision(2)
<< latency << " ms" << std::endl;
}
int main()
{
// 单元测试
std::cout << "正在运行单元测试..." << std::endl;
for (size_t m{1}; m <= 64; ++m)
{
for (size_t n{1}; n <= 64; ++n)
{
assert(verify_transpose_implementation<float>(
&launch_transpose_with_shm_bank_conflict<float>, m, n));
assert(verify_transpose_implementation<float>(
&launch_transpose_without_shm_bank_conflict_via_padding<float>,
m, n));
assert(verify_transpose_implementation<float>(
&launch_transpose_without_shm_bank_conflict_via_swizzling<
float>,
m, n));
}
}
std::cout << "所有单元测试通过!" << std::endl;
// 性能测试
// M: 行数
size_tconst M{8192};
// N: 列数
size_tconst N{8192};
std::cout << M << " x " << N << " 矩阵转置性能测试" << std::endl;
// 测试有bank冲突的版本
floatconst latency_with_shm_bank_conflict{
profile_transpose_implementation<float>(
&launch_transpose_with_shm_bank_conflict<float>, M, N)};
print_latencty("有共享内存Bank冲突的转置",
latency_with_shm_bank_conflict);
// 测试通过填充避免bank冲突的版本
floatconst latency_without_shm_bank_conflict_via_padding{
profile_transpose_implementation<float>(
&launch_transpose_without_shm_bank_conflict_via_padding<float>, M,
N)};
print_latencty("通过填充避免共享内存Bank冲突的转置",
latency_without_shm_bank_conflict_via_padding);
// 测试通过swizzling避免bank冲突的版本
floatconst latency_without_shm_bank_conflict_via_swizzling{
profile_transpose_implementation<float>(
&launch_transpose_without_shm_bank_conflict_via_swizzling<float>, M,
N)};
print_latencty(
"通过Swizzling避免共享内存Bank冲突的转置",
latency_without_shm_bank_conflict_via_swizzling);
return0;
}
程序在配备Intel i9-9900K CPU和NVIDIA RTX 3090 GPU的平台上构建和运行。
$ nvcc transpose.cu -o transpose
$ ./transpose
8192 x 8192 矩阵转置性能测试
有共享内存Bank冲突的转置: 1.10 ms
通过填充避免共享内存Bank冲突的转置: 0.92 ms
通过Swizzling避免共享内存Bank冲突的转置: 0.92 ms
我们可以看到,有共享内存bank冲突的转置kernel 延迟最高,而通过填充和swizzling避免共享内存bank冲突的转置kernel 具有相同的延迟,在这种情况下比有bank冲突的kernel 快20%。
注意这个实现达到了RTX 3090 GPU峰值内存带宽的约65%。如果实现假设矩阵总是填充的(通常使用cudaMallocPitch分配),使得每行继续满足合并要求,性能可以通过向量化内存访问进一步显著提升。
Swizzling vs 填充
Swizzling和填充是处理共享内存bank冲突的两种常见技术。
Swizzling的优点是不会浪费共享内存空间。缺点是实现和理解更复杂,因为索引映射不是线性的。
填充的优点是实现和理解简单。缺点是会浪费共享内存空间,如果填充大小选择不当,可能会破坏数据的地址对齐,特别是当我们使用reinterpret_cast通过大块访问数据时,这会导致未定义行为。这通常发生在对2D填充数组执行向量化内存访问时,意外破坏了数据的对齐。
参考文献
-
CUDA Coalesced Memory Access(https://leimao.github.io/blog/CUDA-Coalesced-Memory-Access/) -
CUDA Shared Memory Bank(https://leimao.github.io/blog/CUDA-Shared-Memory-Bank/) -
Swizzling – Wikipedia(https://en.wikipedia.org/wiki/Swizzling_(computer_graphics)) -
Advanced Performance Optimization in CUDA – NVIDIA GTC 2024(https://www.nvidia.com/en-us/on-demand/session/gtc24-s62192/) -
Using TMA to Transfer Multi-Dimensional Arrays – CUDA Programming Guide(https://docs.nvidia.com/cuda/cuda-c-programming-guide/index.html#using-tma-to-transfer-multi-dimensional-arrays) -
CUtensorMapSwizzle – CUDA Driver API(https://docs.nvidia.com/cuda/cuda-driver-api/group__CUDA__TYPES.html#group__CUDA__TYPES_1g0bc04417bd8ce2c64d204bc3cbc25b58)
(文:GiantPandaCV)

