机器之心报道
机器之心编辑部
如果给小模型更长的思考时间,它们性能可以超越更大规模的模型。
最近一段时间,业内对小模型的研究热情空前地高涨,通过一些「实用技巧」让它们在性能上超越更大规模的模型。
可以说,将目光放到提升较小模型的性能上来有其必然性。对于大语言模型而言,训练时计算(train-time compute)的扩展主导了它们的发展。尽管这种模式已被证明非常有效,但越来越大模型的预训练所需的资源却变得异常昂贵,数十亿美元的集群已经出现。
因此,这一趋势引发了人们对另外一种互补方法的极大兴趣,即测试时计算扩展(test-time compute scaling)。测试时方法不依赖于越来越大的预训练预算,而是使用动态推理策略,让模型在更难的问题上「思考更长时间」。一个突出的例子是 OpenAI 的 o1 模型,随着测试时计算量的增加,它在困难数学问题上表现出持续的进步。
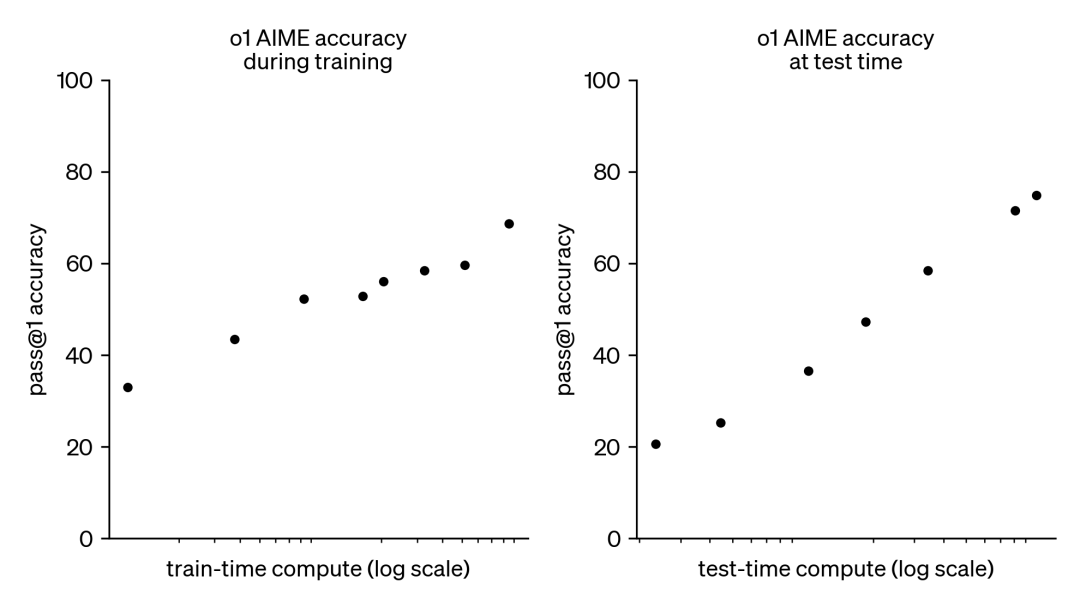
虽然我们不清楚 o1 是如何训练的,但 DeepMind 最近的研究表明,可以通过迭代自我改进或使用奖励模型在解决方案空间上进行搜索等策略来实现测试时计算的最佳扩展。通过自适应地按 prompt 分配测试时计算,较小的模型可以与较大、资源密集型模型相媲美,有时甚至超越它们。当内存受限且可用硬件不足以运行较大模型时,扩展时间时计算尤其有利。然而这种有前途的方法是用闭源模型演示的,没有发布任何实现细节或代码。
DeepMind 论文:https://arxiv.org/pdf/2408.03314
在过去几个月里,HuggingFace 一直在深入研究,试图对这些结果进行逆向工程并复现。他们在这篇博文将介绍:
-
计算最优扩展(compute-optimal scaling):通过实现 DeepMind 的技巧来提升测试时开放模型的数学能力。 -
多样性验证器树搜索 (DVTS):它是为验证器引导树搜索技术开发的扩展。这种简单高效的方法提高了多样性并提供了更好的性能,特别是在测试时计算预算较大的情况下。 -
搜索和学习:一个轻量级工具包,用于使用 LLM 实现搜索策略,并使用 vLLM 实现速度提升。
那么,计算最优扩展在实践中效果如何呢?在下图中,如果你给它们足够的「思考时间」,规模很小的 1B 和 3B Llama Instruct 模型在具有挑战性的 MATH-500 基准上,超越了比它们大得多的 8B、70B 模型。
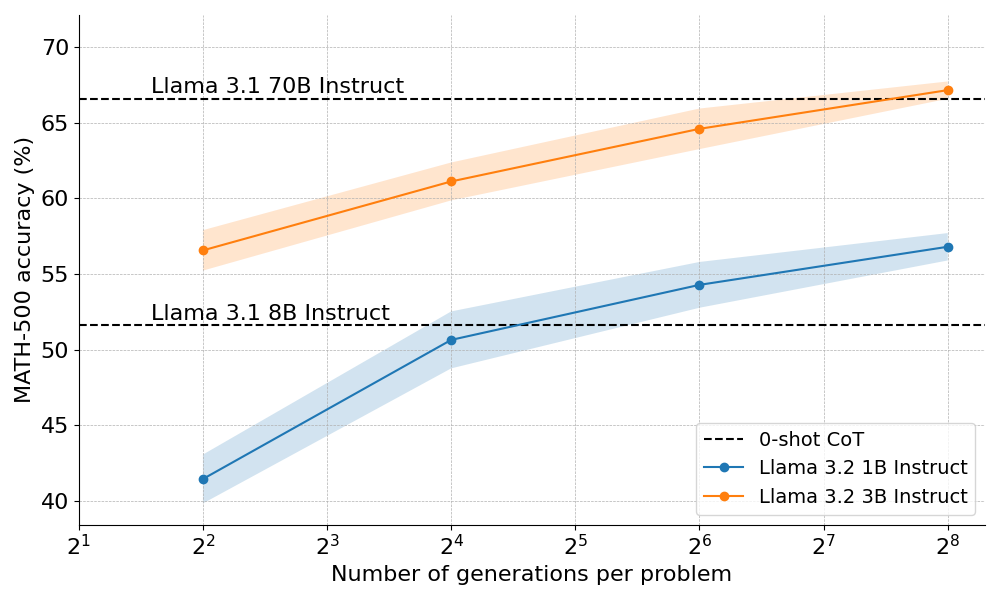
HuggingFace 联合创始人兼 CEO Clem Delangue 表示,在 OpenAI o1 公开亮相仅 10 天后,我们很高兴地揭晓了其成功背后的突破性技术的开源版本:扩展测试时计算。通过给模型更长的「思考时间」,1B 模型可以击败 8B、3B 模型可以击败 70B。当然,完整的技术配方是开源的。

各路网友看到这些结果也不淡定了,直呼不可思议,并认为这是小模型的胜利。
接下来,HuggingFace 深入探讨了产生上述结果背后的原因,并帮助读者了解实现测试时计算扩展的实用策略。
扩展测试时计算策略
扩展测试时计算主要有以下两种主要策略:
-
自我改进:模型通过在后续迭代中识别和纠错来迭代改进自己的输出或「想法」。虽然这种策略在某些任务上有效,但通常要求模型具有内置的自我改进机制,这可能会限制其适用性。 -
针对验证器进行搜索:这种方法侧重于生成多个候选答案并使用验证器选择最佳答案。验证器可以是基于硬编码的启发式方法,也可以是学得的奖励模型。本文将重点介绍学得的验证器,它包括了 Best-of-N 采样和树搜索等技术。这种搜索策略更灵活,可以适应问题的难度,不过它们的性能受到验证器质量的限制。
HuggingFace 专注于基于搜索的方法,它们是测试时计算优化的实用且可扩展的解决方案。下面是三种策略:
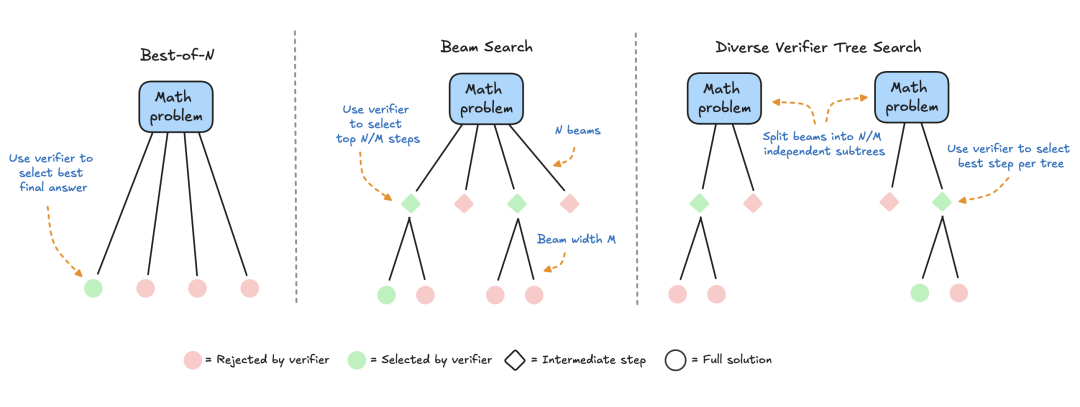
-
Best-of-N:通常使用奖励模型为每个问题生成多个响应并为每个候选答案分配分数,然后选择奖励最高的答案(或稍后讨论的加权变体)。这种方法强调答案质量而非频率。 -
集束搜索:一种探索解决方案空间的系统搜索方法,通常与过程奖励模型 (PRM) 结合使用,以优化问题解决中间步骤的采样和评估。与对最终答案产生单一分数的传统奖励模型不同,PRM 会提供一系列分数,其中推理过程的每个步骤都有一个分数。这种细粒度反馈能力使得 PRM 成为 LLM 搜索方法的自然选择。 -
多样性验证器树搜索 (DVTS):HuggingFace 开发的集束搜索扩展,将初始集束拆分为独立的子树,然后使用 PRM 贪婪地扩展这些子树。这种方法提高了解决方案的多样性和整体性能,尤其是在测试时计算预算较大的情况下。
实验设置
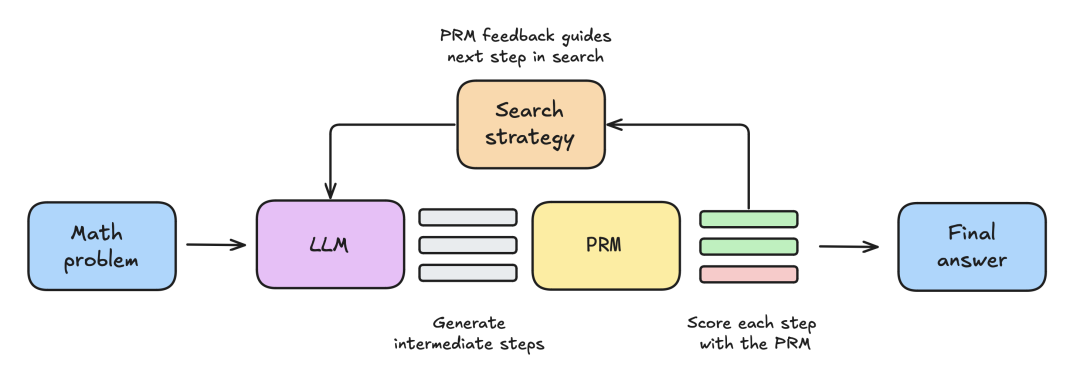
实验设置包括以下步骤:
-
首先给 LLM 提供一个数学问题,让其生成 N 个部分解,例如,推导过程中的中间步骤。 -
每个 step 都由 PRM 评分,PRM 估计每个步骤最终达到正确答案的概率。 -
一旦搜索策略结束,最终候选解决方案将由 PRM 排序以产生最终答案。
为了比较各种搜索策略,本文使用了以下开源模型和数据集:
-
模型:使用 meta-llama/Llama-3.2-1B-Instruct 为主要模型,用于扩展测试时计算; -
过程奖励模型 PRM:为了指导搜索策略,本文使用了 RLHFlow/Llama3.1-8B-PRM-Deepseek-Data,这是一个经过过程监督训练的 80 亿奖励模型。过程监督是一种训练方法,模型在推理过程的每一步都会收到反馈,而不仅仅是最终结果; -
数据集:本文在 MATH-500 子集上进行了评估,这是 OpenAI 作为过程监督研究的一部分发布的 MATH 基准数据集。这些数学问题涵盖了七个科目,对人类和大多数大语言模型来说都具有挑战性。
本文将从一个简单的基线开始,然后逐步结合其他技术来提高性能。
多数投票
多数投票是聚合 LLM 输出的最直接方法。对于给定的数学问题,会生成 N 个候选解,然后选择出现频率最高的答案。在所有的实验中,本文采样了多达 N=256 个候选解,温度参数 T=0.8,并为每个问题生成了最多 2048 个 token。
以下是多数投票应用于 Llama 3.2 1B Instruct 时的表现:
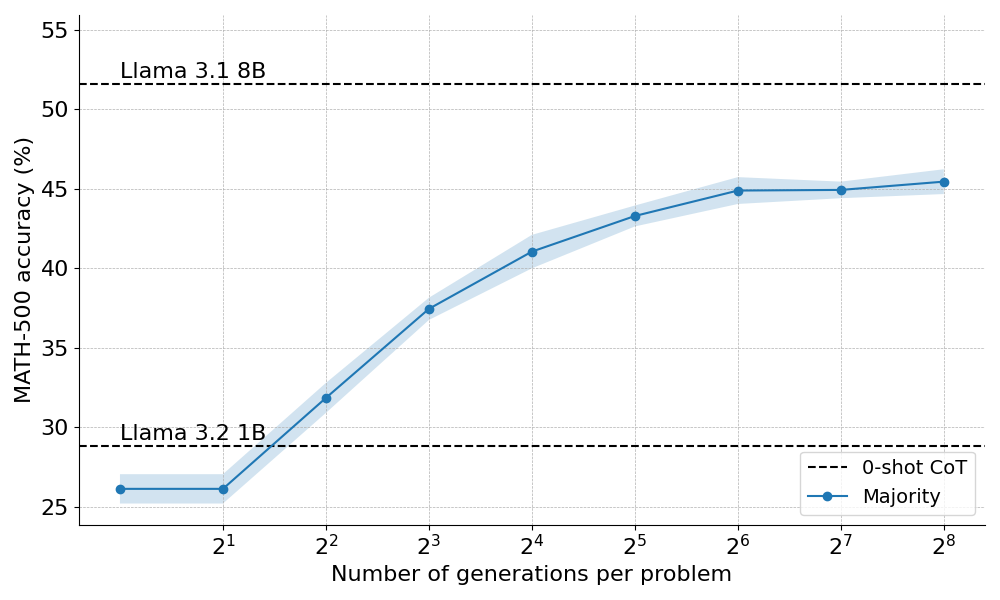
结果表明,多数投票比贪婪解码基线有显著的改进,但其收益在大约 N=64 generation 后开始趋于平稳。这种限制的出现是因为多数投票难以解决需要细致推理的问题。
基于多数投票的局限性,让我们看看如何结合奖励模型来提高性能。
超越多数:Best-of-N
Best-of-N 是多数投票算法的简单且有效的扩展,它使用奖励模型来确定最合理的答案。该方法有两种主要变体:
普通的 Best-of-N:生成 N 个独立响应,选择 RM 奖励最高的一个作为最终回答。这确保了选择置信度最高的响应,但它并没有考虑到回答之间的一致性。
加权 Best-of-N:汇总所有相同响应的得分,并选择总奖励最高的回答。这种方法通过重复出现来提高分数,从而优先考虑高质量的回答。从数学上讲,回答的权重 a_i:
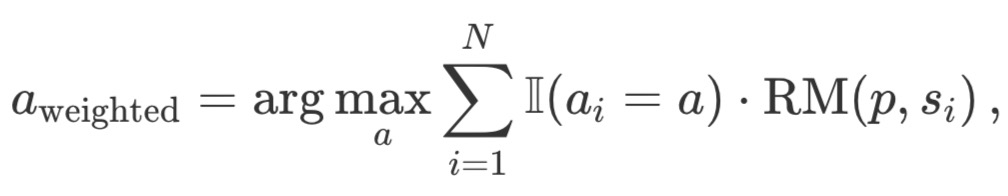
其中,RM (p,s_i) 是对于问题 p 的第 i 个解决方案 s_i 的奖励模型分数。
通常,人们使用结果奖励模型 (ORM) 来获得单个解决方案级别的分数。但为了与其他搜索策略进行公平比较,使用相同的 PRM 对 Best-of-N 的解决方案进行评分。如下图所示,PRM 为每个解决方案生成一个累积的步骤级分数序列,因此需要对步骤进行规约(reduction)以获得单个解决方案级分数:
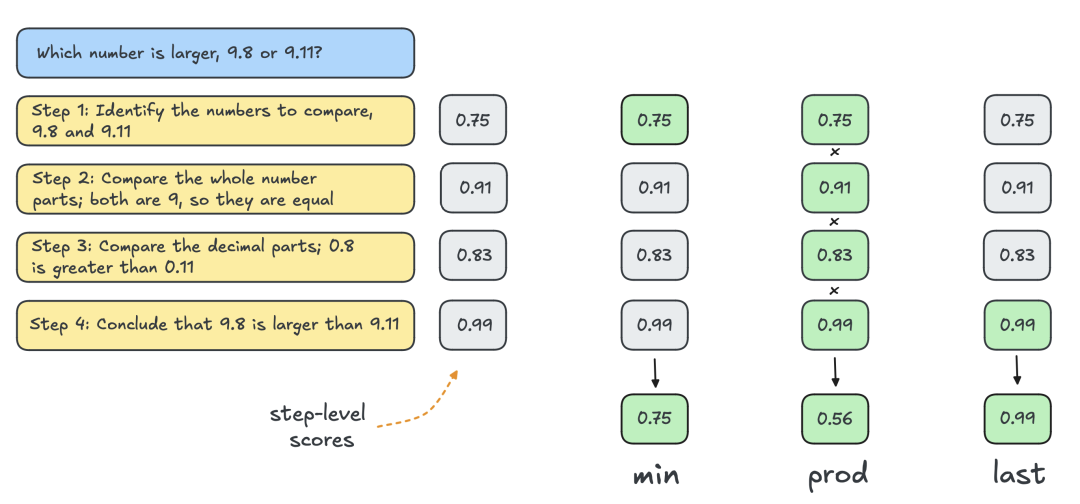
最常见的规约如下:
-
Min:使用所有步骤中的最低分数。
-
Prod:使用阶梯分数的乘积。
-
Last:使用步骤中的最终分数。该分数包含所有先前步骤的累积信息,因此将 PRM 有效地视为能够对部分解决方案进行评分的 ORM。
以下是应用 Best-of-N 的两种变体得到的结果:
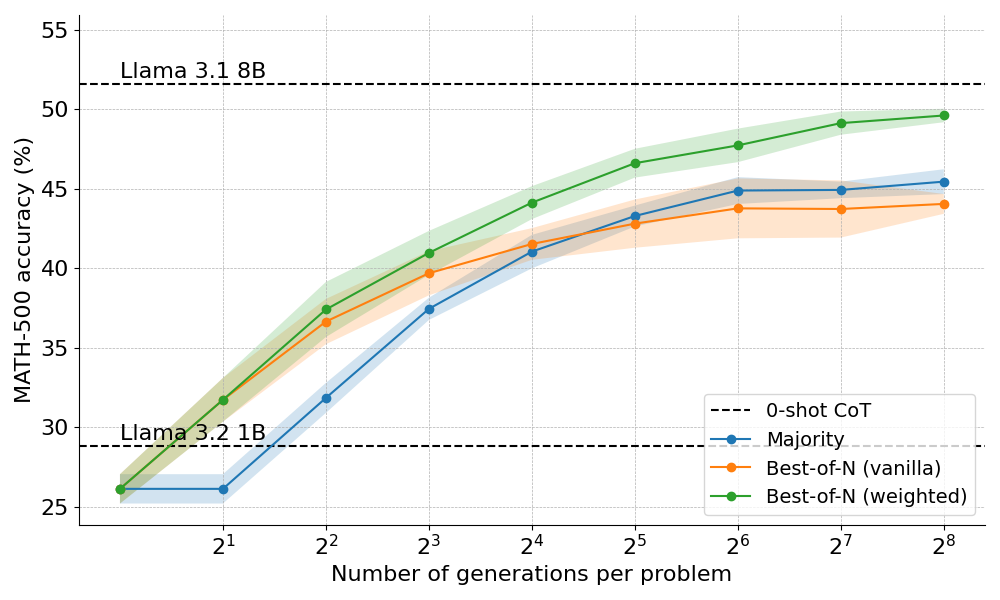
结果揭示了一个明显的优势:加权的 Best-of-N 始终优于普通的 Best-of-N,特别是在发电预算较大的情况下。它能够汇总相同答案的分数,确保即使频率较低但质量较高的答案也能得到有效的优先处理。
然而,尽管有这些改进,仍然达不到 Llama 8B 模型所达到的性能,并且在 N=256 时 Best-of-N 方法开始趋于稳定。
可以通过逐步监督搜索过程来进一步突破界限吗?
使用 PRM 的集束搜索
作为一种结构化搜索方法,集束搜索可以系统地探索解决方案空间,使其成为在测试时改进模型输出的强大工具。与 PRM 结合使用时,集束搜索可以优化问题解决中中间步骤的生成和评估。集束搜索的工作方式如下:
-
通过保持固定数量的「集束」或活动路径 N ,迭代生成多个候选解决方案。 -
在第一次迭代中,从温度为 T 的 LLM 中抽取 N 个独立步骤,以引入响应的多样性。这些步骤通常由停止标准定义,例如终止于新行 \n 或双新行 \n\n。 -
使用 PRM 对每个步骤进行评分,并选择前 N/M 个步骤作为下一轮生成的候选。这里 M 表示给定活动路径的「集束宽度」。与 Best-of-N 一样,使用「最后」的规约来对每次迭代的部分解决方案进行评分。 -
通过在解决方案中采样 M 个后续步骤来扩展在步骤 (3) 中选择的步骤。 -
重复步骤 (3) 和 (4),直到达到 EOS token 或超过最大搜索深度。
通过允许 PRM 评估中间步骤的正确性,集束搜索可以在流程早期识别并优先考虑有希望的路径。这种逐步评估策略对于数学等复杂的推理任务特别有用,这是因为验证部分解决方案可以显著改善最终结果。
实现细节
在实验中,HuggingFace 遵循 DeepMind 的超参数选择,并按照以下方式运行集束搜索:
-
计算扩展为 4、16、64、256 时的 N 个集束 -
固定集束宽度 M=4 -
在温度 T=0.8 时采样 -
最多 40 次迭代,即最大深度为 40 步的树
如下图所示,结果令人震惊:在 N=4 的测试时预算下,集束搜索实现了与 N=16 时 Best-of-N 相同的准确率,即计算效率提高了 4 倍!此外,集束搜索的性能与 Llama 3.1 8B 相当,每个问题仅需 N=32 解决方案。计算机科学博士生在数学方面的平均表现约为 40%,因此对于 1B 模型来说,接近 55% 已经很不错了!
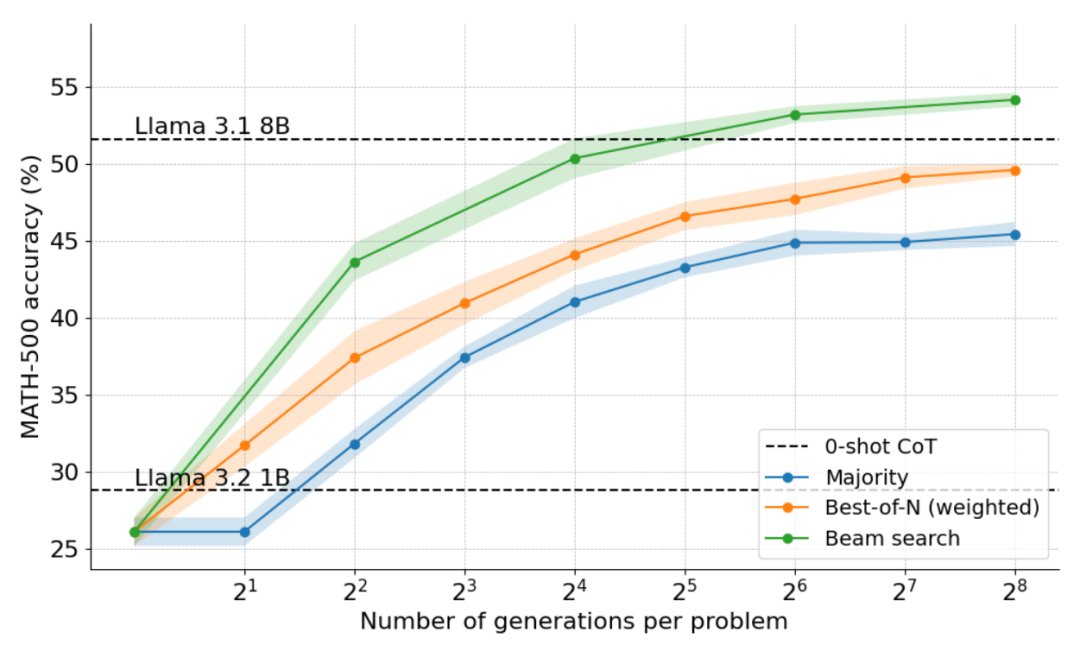
哪些问题集束搜索解决得最好
虽然总体上很明显,集束搜索是一种比 Best-of-N 或多数投票更好的搜索策略,但 DeepMind 的论文表明,每种策略都有权衡,这取决于问题的难度和测试时计算预算。
为了了解哪些问题最适合哪种策略,DeepMind 计算了估计问题难度的分布,并将结果分成五等分。换句话说,每个问题被分配到 5 个级别之一,其中级别 1 表示较容易的问题,级别 5 表示最难的问题。为了估计问题难度,DeepMind 为每个问题生成了 2048 个候选解决方案,并进行了标准采样,然后提出了以下启发式方法:
-
Oracle:使用基本事实标签估计每个问题的 pass@1 分数,对 pass@1 分数的分布进行分类以确定五分位数。 -
模型:使用每个问题的平均 PRM 分数分布来确定五分位数。这里的直觉是:更难的问题分数会更低。
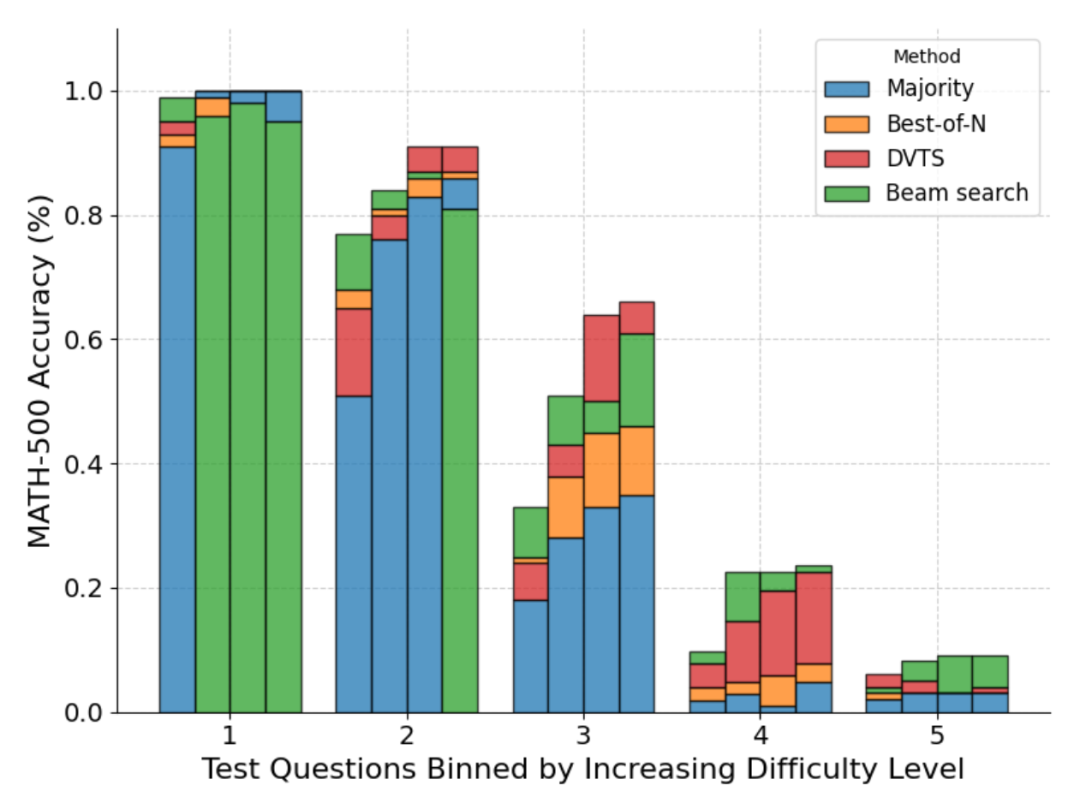
下图是根据 pass@1 分数和四个测试时计算预算 N=[4,16,64,256] 对各种方法的细分:
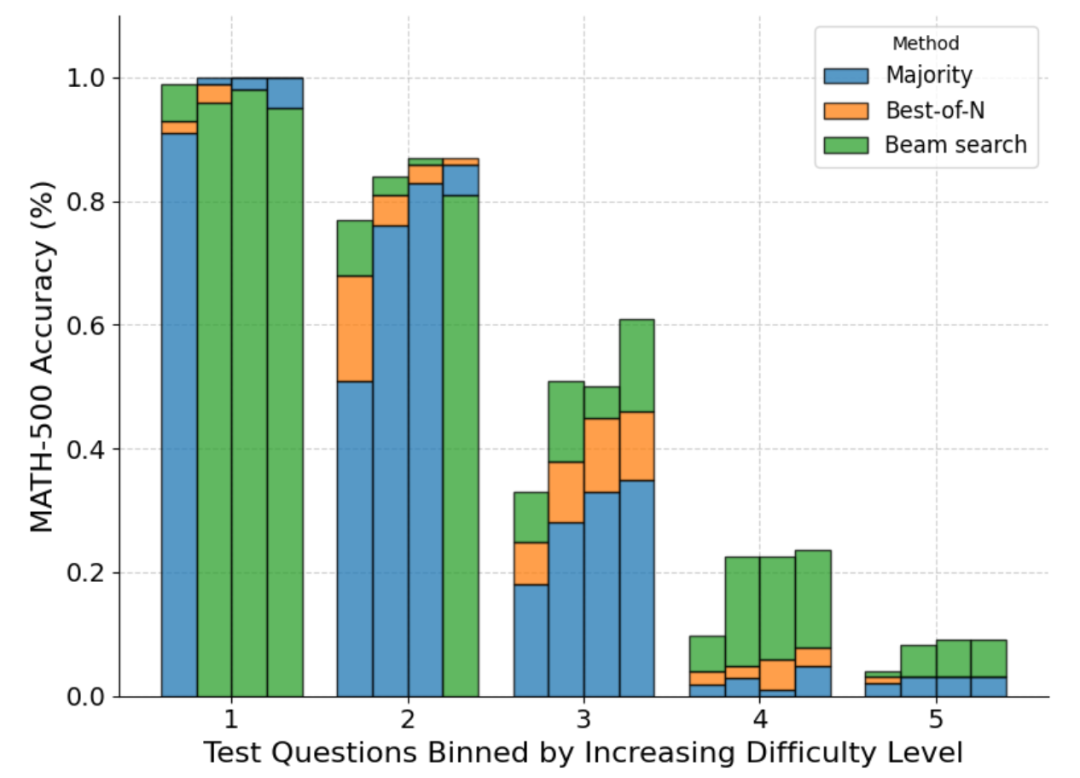
可以看到,每个条形表示测试时计算预算,并且在每个条形内显示每种方法的相对准确度。例如在难度等级 2 的四个条形中:
多数投票是所有计算预算中表现最差的方法,除了 N=256(集束搜索表现最差)。
集束搜索最适合 N=[4,16,64],但 Best-of-N 最适合 N=256。
应该说,集束搜索在中等难度和困难难度问题(3-5 级)中取得了持续的进展,但在较简单问题上,尤其是在计算预算较大的情况下,它的表现往往比 Best-of-N(甚至多数投票)更差。
通过观察集束搜索生成的结果树,HuggingFace 意识到,如果单个步骤被分配了高奖励,那么整棵树就在该轨迹上崩溃,从而影响多样性。这促使他们探索一种最大化多样性的集束搜索扩展。
DVTS:通过多样性提升性能
正如上面所看到的,集束搜索比 Best-of-N 具有更好的性能,但在处理简单问题和测试时计算预算较大时往往表现不佳。
为了解决这个问题,HuggingFace 开发了一个扩展,称之为「多样性验证器树搜索」(DVTS),旨在最大限度地提高 N 较大时的多样性。
DVTS 的工作方式与集束搜索类似,但有以下修改:
-
对于给定的 N 和 M,将初始集束扩展为 N/M 个独立子树。 -
对于每个子树,选择具有最高 PRM 分数的步骤。 -
从步骤 (2) 中选择的节点生成 M 个新步骤,并选择具有最高 PRM 分数的步骤。 -
重复步骤 (3),直到达到 EOS token 或最大树深度。
下图是将 DVTS 应用于 Llama 1B 的结果:
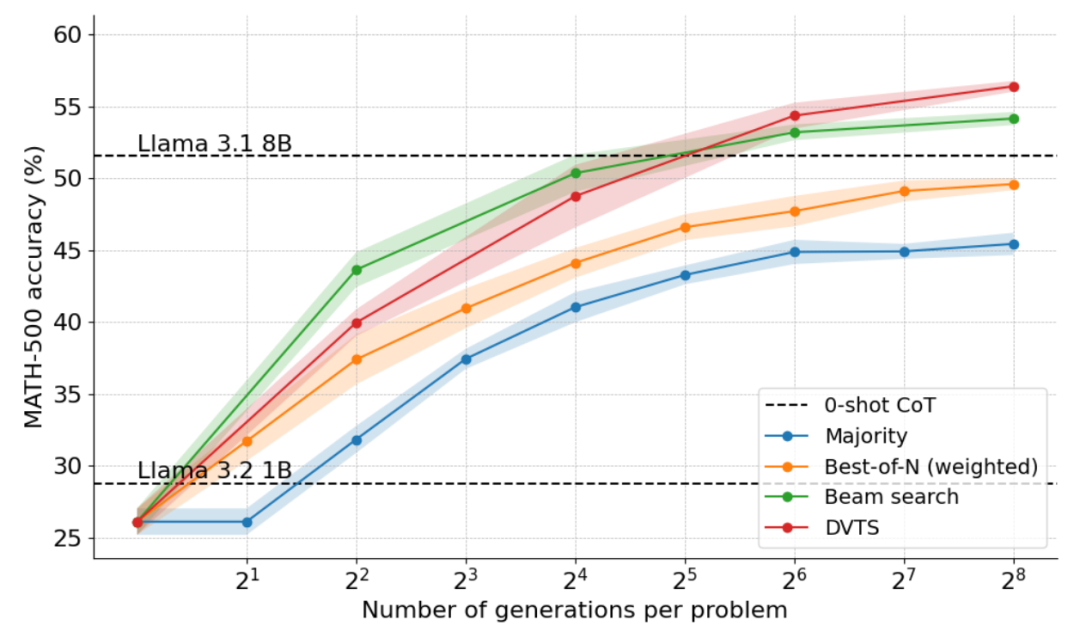
可以看到,DVTS 为集束搜索提供了一种补充策略:在 N 较小时,集束搜索更有效地找到正确的解决方案;但在 N 较大时,DVTS 候选的多样性开始发挥作用,可以获得更好的性能。
此外在问题难度细分中,DVTS 在 N 较大时提高了简单 / 中等问题的性能,而集束搜索在 N 较小时表现最佳。
计算 – 最优扩展(compute-optimal scaling)
有了各种各样的搜索策略,一个自然的问题是哪一个是最好的?在 DeepMind 的论文中(可参考《Scaling LLM Test-Time Compute Optimally can be More Effective than Scaling Model Parameters 》),他们提出了一种计算 – 最优扩展策略,该策略可以选择搜索方法和超参数 θ,以便在给定的计算预算 N 下达到最佳性能:
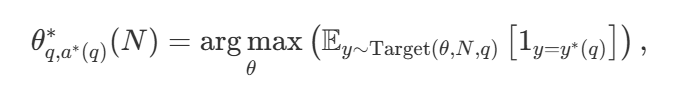
其中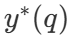 是问题 q 的正确答案。
是问题 q 的正确答案。 表示计算 – 最优的扩展策略。由于直接计算
表示计算 – 最优的扩展策略。由于直接计算 有些棘手,DeepMind 提出了一种基于问题难度的近似方法,即根据哪种搜索策略在给定难度级别上达到最佳性能来分配测试时的计算资源。
有些棘手,DeepMind 提出了一种基于问题难度的近似方法,即根据哪种搜索策略在给定难度级别上达到最佳性能来分配测试时的计算资源。
例如,对于较简单的问题和较低的计算预算,最好使用 Best-of-N 等策略,而对于较难的问题,集 shu 搜索是更好的选择。下图为计算 – 最优曲线!
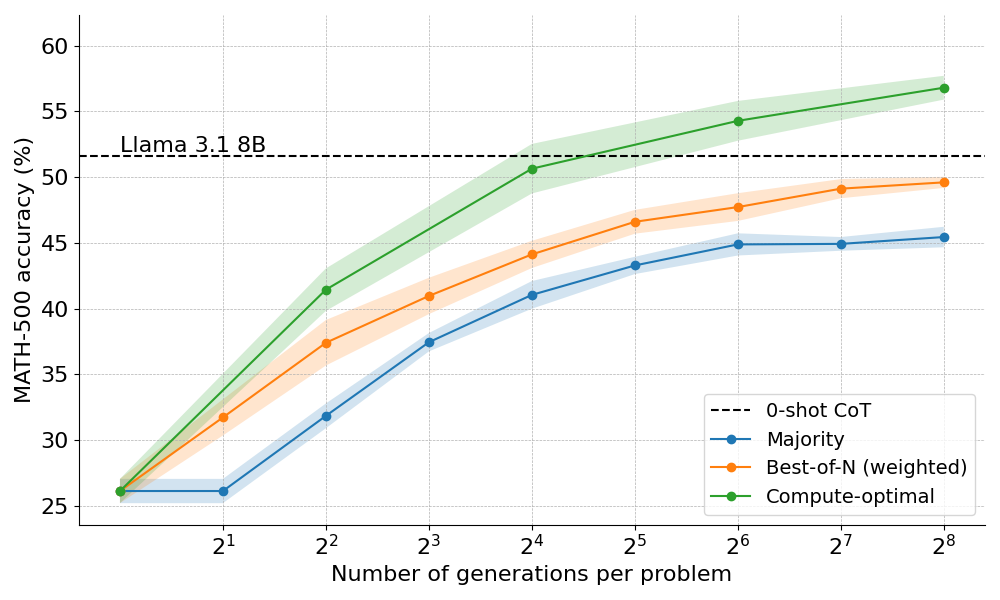
扩展到更大的模型
本文还探索了将计算 – 最优(compute-optimal)的方法扩展到 Llama 3.2 3B Instruct 模型,以观察 PRM 在与策略自身容量相比时在哪个点开始减弱。结果显示,计算 – 最优的扩展效果非常好,3B 模型的性能超过了 Llama 3.1 70B Instruct(后者是前者大小的 22 倍!)。
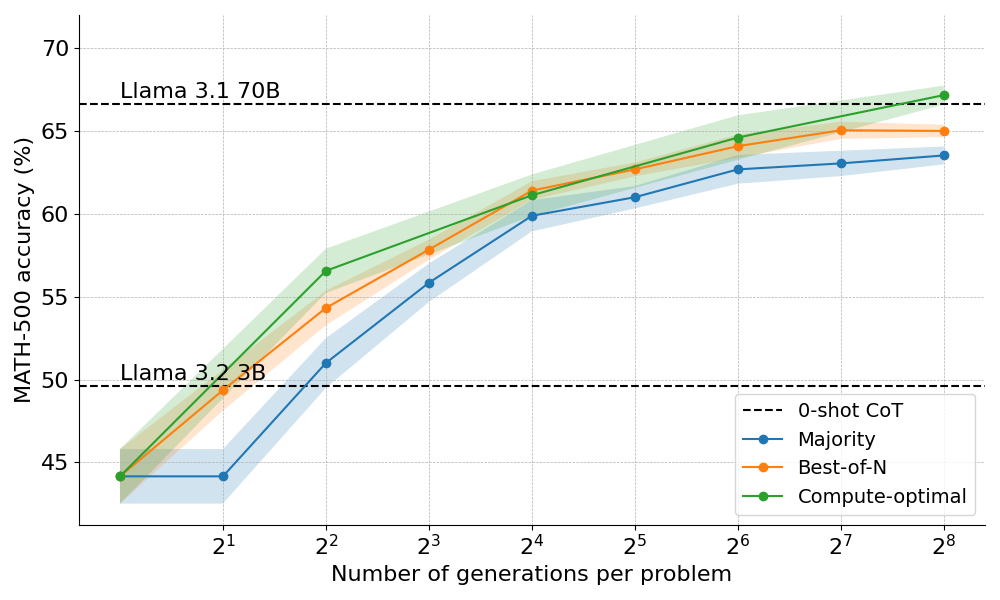
接下来该怎么办?
对测试时计算扩展的探索揭示了利用基于搜索的方法的潜力和挑战。展望未来,本文提出了几个令人兴奋的方向:
-
强验证器:强验证器在提高性能方面发挥着关键作用,提高验证器的稳健性和通用性对于推进这些方法至关重要; -
自我验证:最终目标是实现自我验证,即模型可以自主验证自己的输出。这种方法似乎是 o1 等模型正在做的事情,但在实践中仍然难以实现。与标准监督微调 (SFT) 不同,自我验证需要更细致的策略; -
将思维融入过程:在生成过程中融入明确的中间步骤或思维可以进一步增强推理和决策能力。通过将结构化推理融入搜索过程,可以在复杂任务上实现更好的表现; -
搜索作为数据生成工具:该方法还可以充当强大的数据生成过程,创建高质量的训练数据集。例如,根据搜索产生的正确轨迹对 Llama 1B 等模型进行微调可以带来显著的收益。这种基于策略的方法类似于 ReST 或 V-StaR 等技术,但具有搜索的额外优势,为迭代改进提供了一个有希望的方向; -
调用更多的 PRM:PRM 相对较少,限制了其更广泛的应用。为不同领域开发和共享更多 PRM 是社区可以做出重大贡献的关键领域。
(文:机器之心)
