
近日,中山大学计算机学院与腾讯微信搜索团队联合提出 Q-RM(Q-function Reward Model),在 ICML 2025 正式发表。
这一方法专注于构建更精确的 token-level 奖励信号,是对齐训练中一个关键突破,显著提升了大语言模型的训练效率和效果。该研究由中山大学计算机学院与腾讯微信搜索团队共同完成。

论文标题:
Discriminative Policy Optimization for Token-Level Reward Models
论文地址:
https://arxiv.org/abs/2505.23363
开源地址:
https://github.com/homzer/Q-RM

背景和挑战:过程监督太粗,DPO-RM奖励不准
结果级奖励模型(Outcome Reward Model, ORM):仅对完整回答打分,反馈过于稀疏,难以指导多步推理;
过程级奖励模型(Process Reward Model, PRM):逐步评分但粒度仍粗,通常以句子为单位,并依赖人工标注;
DPO-RM 模型:结合 DPO(Direct Preference Optimization)与偏好数据,提供 token-level 奖励,但存在两大缺陷:① 奖励与语言模型的生成概率强耦合,可能导致“高置信错答”;② 奖励计算依赖参考模型 ,引入额外计算与偏差。

判别式策略模型(Discriminative Policy)
为了解决 DPO-RM 的上述问题,论文提出了基于判别式策略(Discriminative Policy)的奖励模型 Q-RM,把奖励建模和语言生成彻底“拆开”。判别式模型的表达式为:

其中 为 logits。判别式策略模型 和以往的策略模型 不同, 只需要输入当前状态 ,再给出动作 的概率; 需要同时输入当前状态 和动作 ,再去衡量动作 的概率。
Q-RM 不像 DPO-RM 那样保留语言生成的能力,而是专注于对每个 token 及其上下文进行评分,以提供更准确的 token-level 奖励信号。
在 DPO 中奖励信号的表达式为:
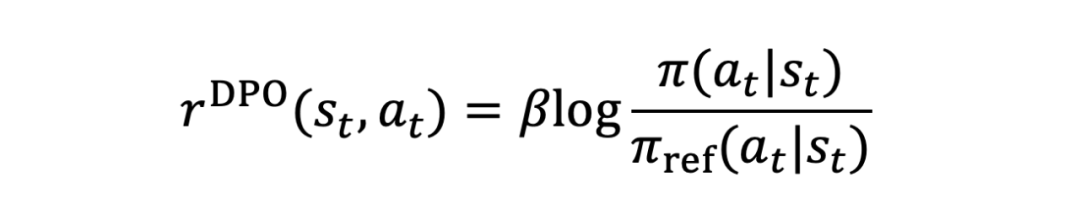
而在 Q-RM 中奖励信号的表达式为:
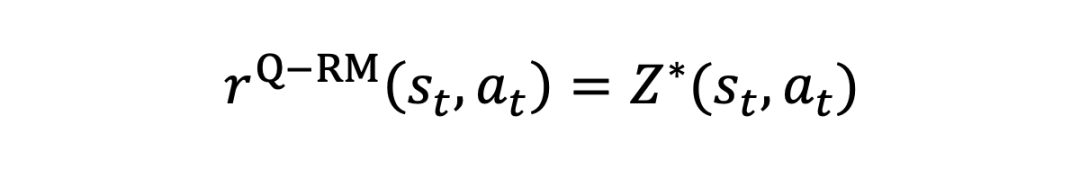
其中 为 logits,由 LLM 主干网络最后一层隐藏层输出的(sequence-length,hidden-size)张量,经一个(hidden-size,1)的线性层映射后,得到(sequence-length,1)的结果。其训练方法为:
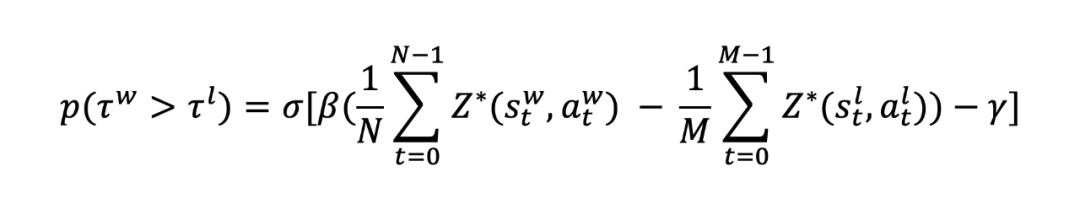
其中 来自偏好数据集,N 和 M 分别是序列的长度, 和 分别是超参数。论文中发现 和 有着等价的关系(只差一个常数项的差异),完整证明过程请参考原文。
这中奖励建模方式做彻底解耦奖励建模和语言生成,奖励模型不再直接依赖 的生成概率,避免了高置信度但错误的 token 被高奖励“误导”,消除了对参考模型的依赖,从而显著提高奖励分配的准确性和训练稳定性。
例如下面的例子中:DPO-RM 高分集中在 “\n” 换行等无关 token,正确答案中真正关键数字 “0.05”“133” 得分并不突出,同时错位答案中的 “$135” 只给出中性甚至偏高分。
与之相反,Q-RM 明确把高分给 “0.05”“133”等关键的正确推导步骤 token,对换行等符号给分接近 0,对错误 token “$135” 等显著扣分,对中性 token 不做过多惩罚。
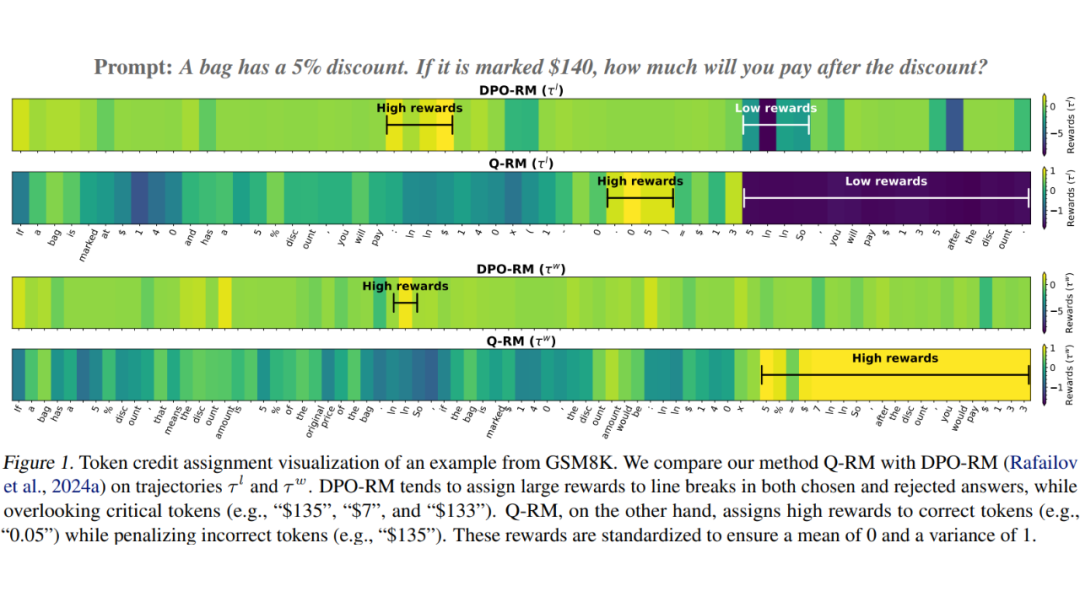

Q-RM 中 Q 的由来
论文提出了 Q-function as Reward Model(Q-RM),其中 Q-function 就是强化学习中的 Q 函数。论文在 Proposition 3.4 中说明了 Q-RM 的奖励信号 和 具有如下线性关系:
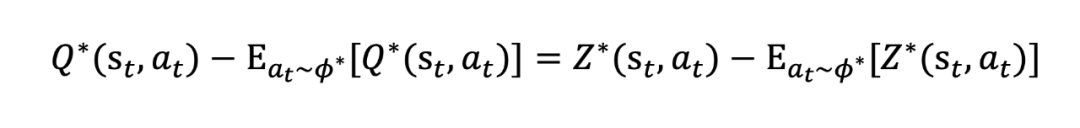
即最优 Q 函数和最优 logits 之间仅存在一个常数量级的误差。此外,在该等式的左边即为优势函数 A 的定义。该公式说明了使用 计算优势函数与 Q 函数计算优势函数完全等价。以下给出这条公式的简要推导过程(详细过程请参照论文附录 C)。根据论文公式 6:
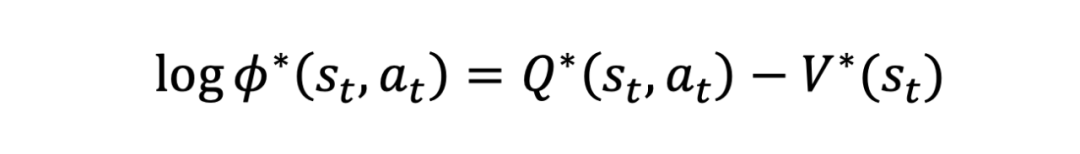
其中 为最大熵理论下的价值函数,其表达式为:
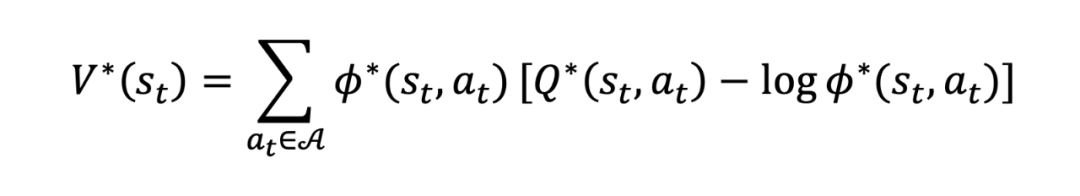
为最优判别式策略模型,其表达式为:
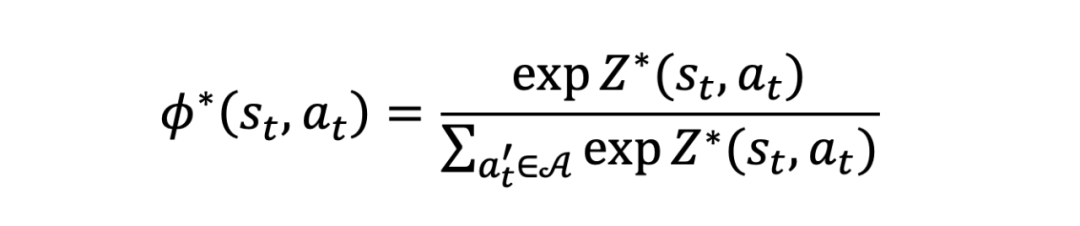
将上述两个式子代入到公式 6 并进行简单移项就得到(公式 36):
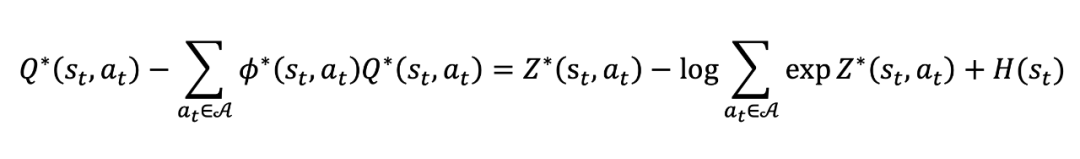
其中 为熵。对公式 36 两边取期望就得到(公式 38):
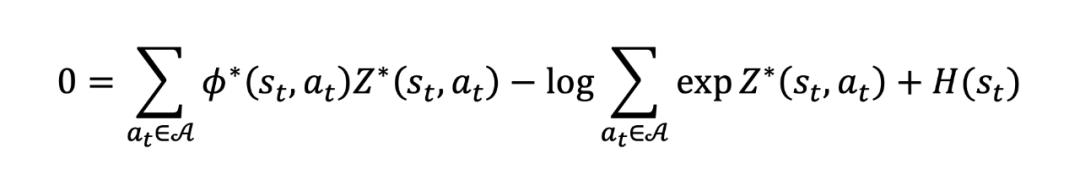
将公式 38 代回到公式 36 就得到:
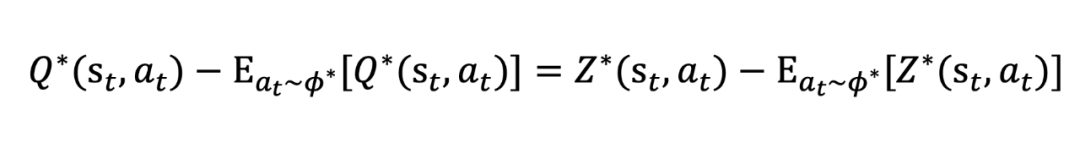

Q-RM 算法流程
Q-RM 的输出结果 与 存在等价的关系,可以容易地得到优势函数,无缝衔接到目前已有的强化学习算法中;(例如 PPO 和 Reinforce)。


值得注意的是:Q-RM 给出的 已经是一种 token-level Q 值,无需再滚动累积后续奖励(如);直接计算 就足够精准。去除了 、 两个手动超参,提升训练稳定性。

实验验证
主实验
论文在数学任务(GSM8K、MATH)和通用问答任务(QA-Feedback、AlpacaEval2.0)上进行测试,结果如下:
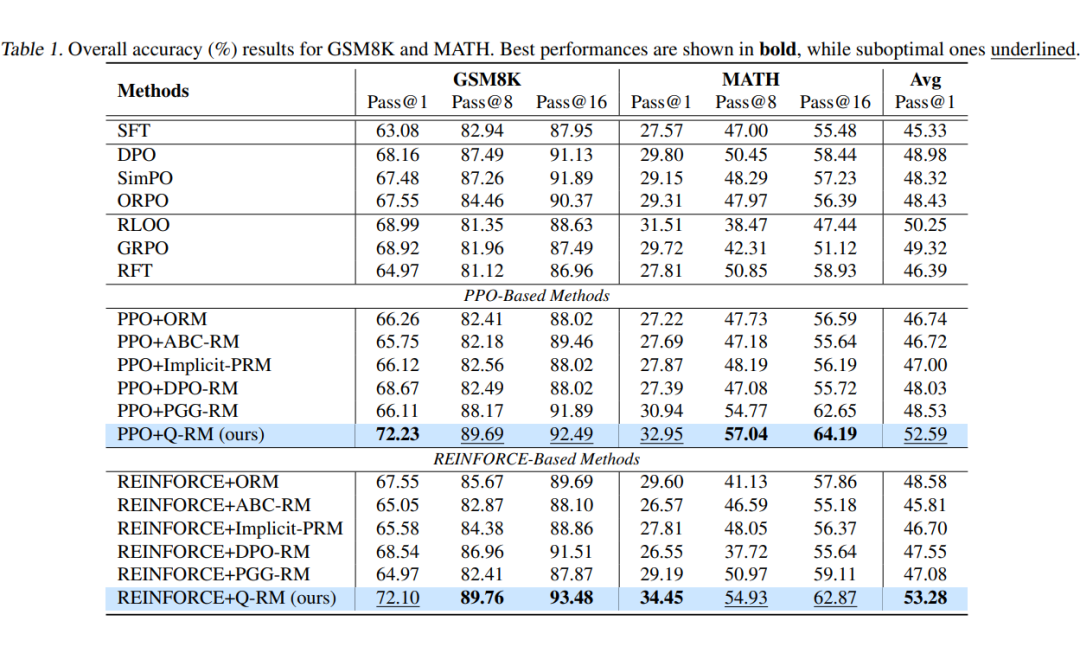
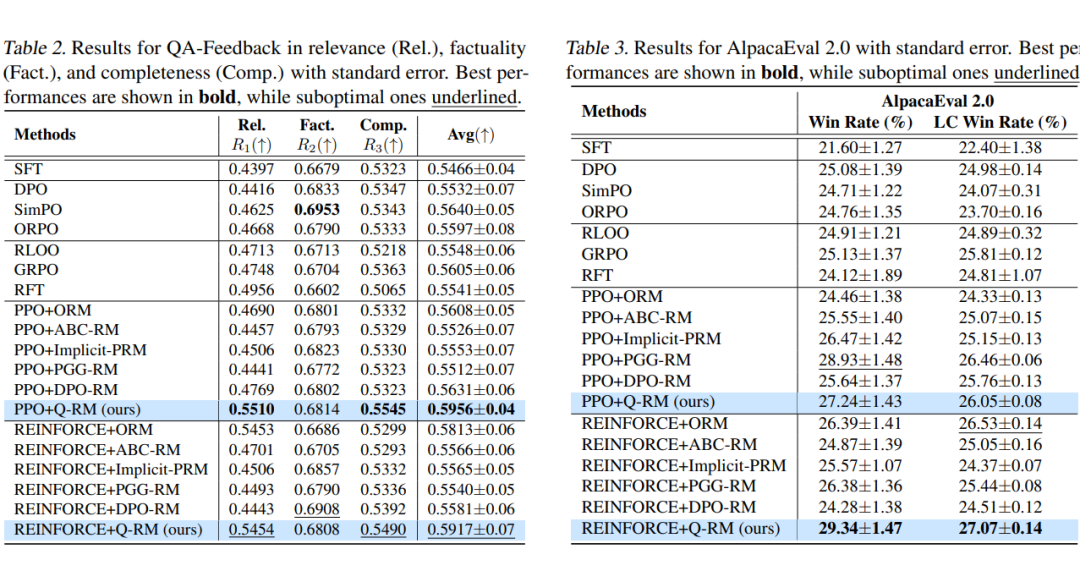
Q-RM 引导的 RL 训练在多项基准任务上都取得了最好的效果。
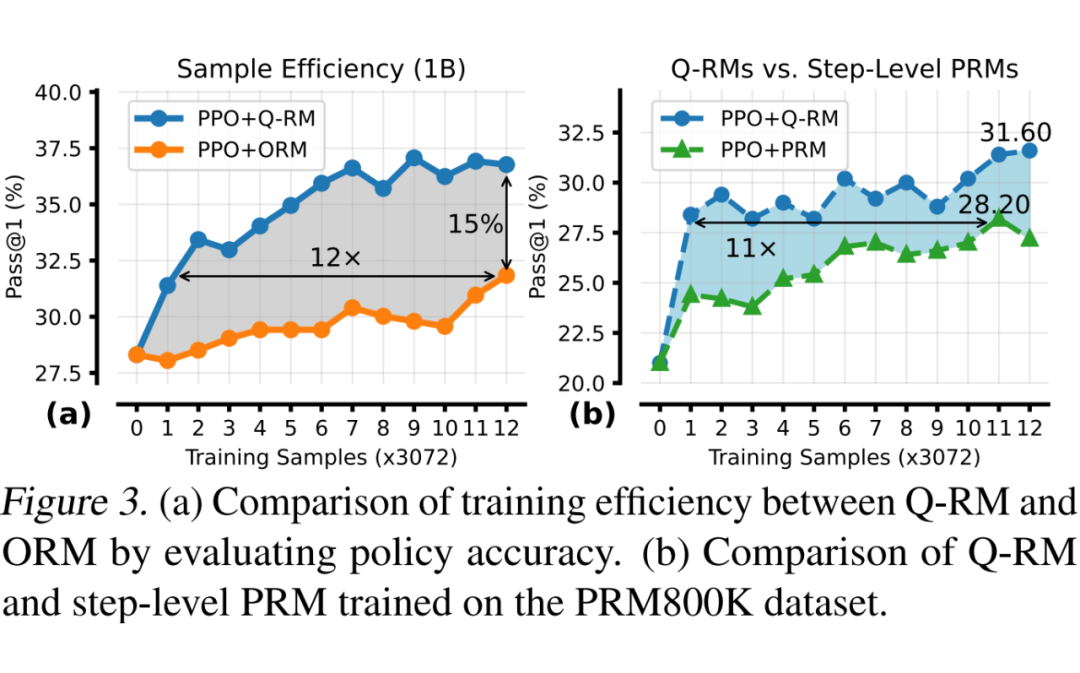
与传统的 step-Level PRM 和 ORM 相比,Q-RM 取得了更高的训练效率(1/12~1/11 的训练样本就取得了相同的 pass@1),以及训练后更好的 pass@1。

总结
论文基于最大熵框架,从理论上证明了最优 logits 和最优 Q 函数之间存在常数量级的线性关系,简化了 token-level 优势函数的计算。并基于该理论提出了 Q-RM 细粒度奖励模型。Q-RM 无需细粒度标注标签,仅需要常见的偏好数据集就能够训练出 token-level 的 Q 函数。
(文:PaperWeekly)

