截止到目前，包括hf在内已有很多组织尝试完整复现R1-Zero，但目前开源的一些项目主要还是聚焦到简单场景和小size模型上（以qwen-7b系列为主）

完整复现出R1-Zero的test scaling曲线并不是一件容易的事，需要高质量的数据，较大size的模型。本文尝试总结与记录我们完整复现R1-Zero的过程。

已有的开源项目参考

• https://github.com/huggingface/open-r1
• https://github.com/hkust-nlp/simpleRL-reason?tab=readme-ov-file
• https://oatllm.notion.site/oat-zero
• https://github.com/Jiayi-Pan/TinyZero

从7b出发

复现simple RL

tinyZero的任务场景过于简单，因此我们尝试先从simpleRL的复现入手。选择simpleRL的理由，是因为其所用的训练数据相对简单，模型7b很好训练，能很快获取一个数据和算法认知，以便更好地帮助我们在32b以及72b模型上训练。

训练数据

math training 3-5levelsimpleRL的训练数据使用的是chat格式：

<|im_start|>system\nPlease reason step by step, and put your final answer within \\boxed{}.<|im_end|>\n<|im_start|>user\nLet $a$ and $b$ be the two real values of $x$ forwhich\\[\\sqrt[3]{x} + \\sqrt[3]{20 - x} = 2\\]The smaller of the two values can be expressed as $p - \\sqrt{q}$, where$p$ and $q$ are integers. Compute $p + q$.<|im_end|>\n<|im_start|>assistant

我们同时基于R1提供的prompt制作了以下格式数据：

A conversation between User and Assistant. The user asks a question, and the Assistant solves it. The assistant first thinks about the reasoning process in the mind and then provides the user with the answer, ensuring that the final result in the answer is enclosed in \\boxed{{}}. The reasoning process and answer are enclosed within '<think>''</think>' and '<answer>''</answer>' tags, respectively, i.e., <think> reasoning process here </think> <answer> answer here </answer>. User: Let $a$ and $b$ be the two real values of $x$ forwhich\\[\\sqrt[3]{x} + \\sqrt[3]{20 - x} = 2\\]The smaller of the two values can be expressed as $p - \\sqrt{q}$, where$p$ and $q$ are integers. Compute $p + q$. Assistant:

注意这里第二种格式的情况，eos需要用</answer>来表示，那么就有两种做法，prompt中明确提示用</answer>结尾或者修改generation配置，两者测试下来差异并不会很大，但会影响resps lens的观测

评测

math500 && AIME24

reward

针对第一种prompt，format的判定为respsonse中是否出现\\boxed字段

第二种prompt的话，format的判定为response是否满足<think> reasoning process here </think> <answer> answer here </answer>的格式要求并且出现\\boxed字段

奖励分成三种情况：

• 不满足format：-1
• 满足format，answer错误：0
• 满足format，answer正确：1

判断函数使用math-verifiy和qwen-eval

基座与算法

分别对比了qwen-7b base与qwen-7b math base的效果

并对比了GRPO和PPO的效果差异

实验结论

1. qwen-7b ppo上测试两种prompt的区别，resps lens上第二种prompt会出现先下降后增加（快速拟合pattern并学习eos），第一种则是很快增加后基本不变，但是二者的eval效果接近。为什么lens先下降后上升，因为我们并没有去以</answer>做为结束的标志，而是通过提示让模型自己生成eos，但模型前期并不稳定，eos学的不好，所以前期通过format的约束会出现lens迅速下降去拟合正确结束的格式，然后在后期慢慢变长。

两个prompt的区别是第二种prompt更适合pretrain model，本身是个续写任务，而第一种则是chat格式，更适合sft（因为qwen做过cpt，所以有这个chat格式的qa数据，也不用担心special token没有训练过）。但整体上来讲第二种prompt更有利于涌现long cot，一个是格式pattern会收缩探索空间（减少极端负例），另一个是这种续写出来的答案更自然。

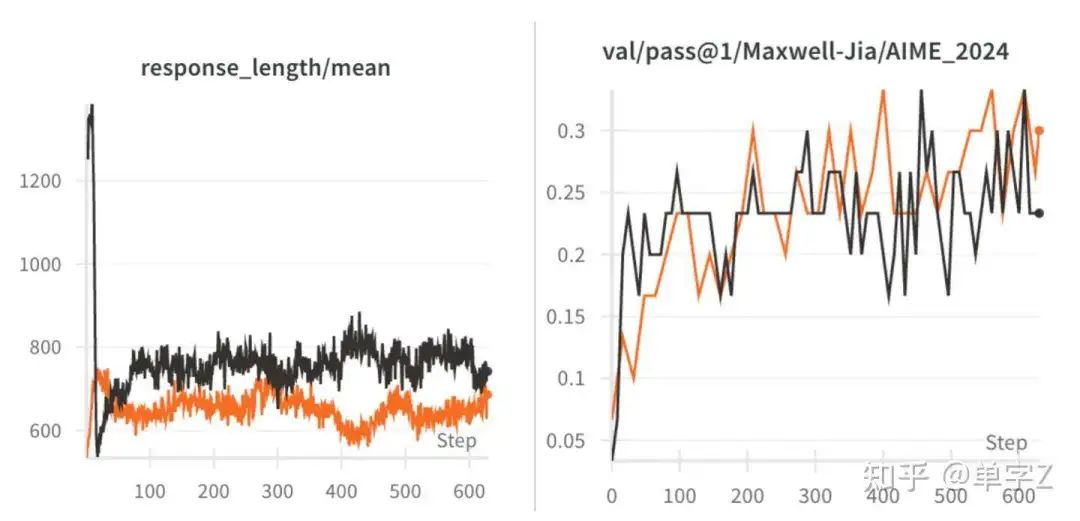
2. qwen 7b上为什么没有明显观测到cot变长的现象？

我们后续又增加了几组实验验证了，cot变长可能和两个因素有关系，训练的步数和query的难度，simpleRL所用的math数据在后期train acc已经收敛到90以上，所以无法在该训练集上进一步出现cot变长的现象。但当切换到另一个较难数据集上时，在1k步能明显观测到cot变长至1.2k tokens，但限于7b的能力，train acc也只能收敛到0.25，继续训练意义不大

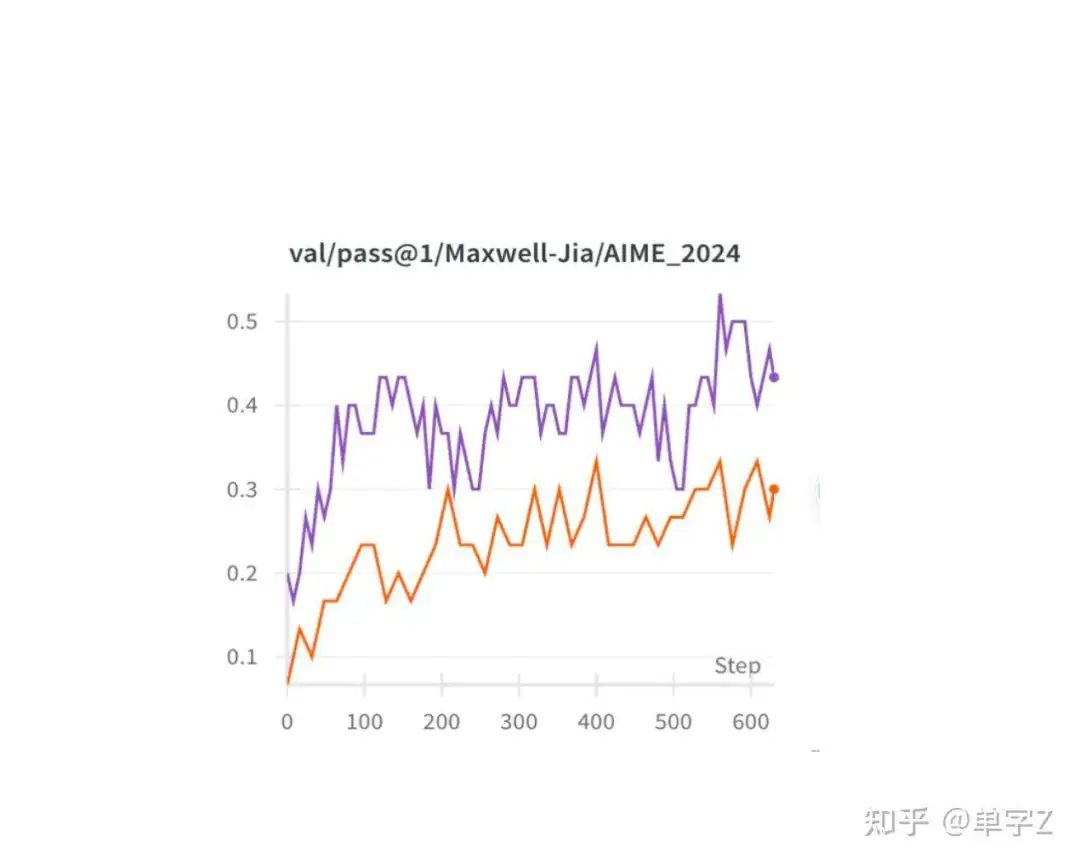
3. ppo上测试结果表明qwen math-7b更优于qwen-7b，AIME24最后可以到0.5（在线测的数据是这个Maxwell-Jia/AIME_2024)，实际上离线用qwen的包跑测和simpleRL的结果一致为0.37，AIME的数据还不一样？），math 0.77

这个是和cpt有直接关系的，所以如果像拿到较高的zero效果，cpt应该也是重要的一个环节

4. ppo和grpo的效果基本持平

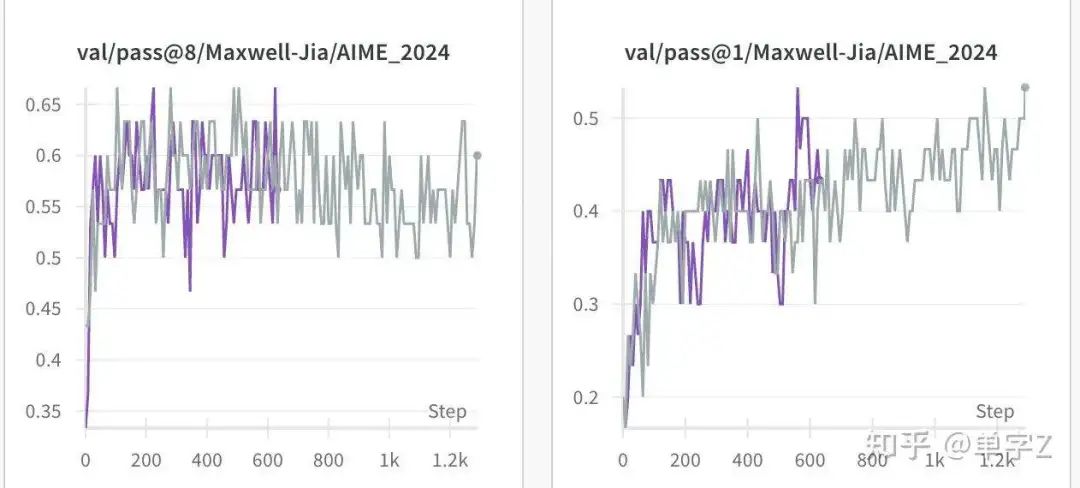
其他的一些takeaway：

1. 不使用fomat reward的话，eval的效果会低一些，response lens也不能观测到增长的趋势，这个可能和模型大小有关，也和探索空间过大有关
2. 一个ppo epoch的mini-batch切分不能太多次更新，太offpolicy的话会导致训练缓慢甚至训崩，ppo对这个很敏感，我们尝试用simpleRL的超参发现并不好用
3. GRPO在效果和效率上与PPO差别不大，而且超参更好调，scaling的话grpo会更好
4. qwen-7bmath的反思行为在初始阶段就会多于qwen-7b，这和math的cpt应该是有比较大的关系
5. qwen-7bmath并没观测到resps lens明显变长，可能是和训练集数量比较少有关，但是观察输出发现7bmath会吐很多代码等无关信息，所以后续大size不选用math系列
6. 可以用pass8或者16描述模型上限，这对后续指标观察意义比较大，pass1应该随着训练逼近pass8，如果pass1，pass8，train acc都不涨了那就说明算法应该出问题了

迈向32b

通过7b的实验我们能够很清晰的认识到，复现zero需要的条件：

• 正确的prompt
• 相对较难的query
• 较长的训练步数，long cot涌现是个缓慢过程
• size更大的模型

训练数据

整合开源和内部数据，准备了较高质量的3w+条，qwen7b math的准确率在这份数据集上只有20%，保证了难度覆盖。同时prompt形式采用了第二种，即r1的提供的prompt格式

算法

采用GRPO，一个是方便训练，另一个是调参相对简单

实验

1.更大size的模型更容易涌现long cot，下图是resps len的对比图

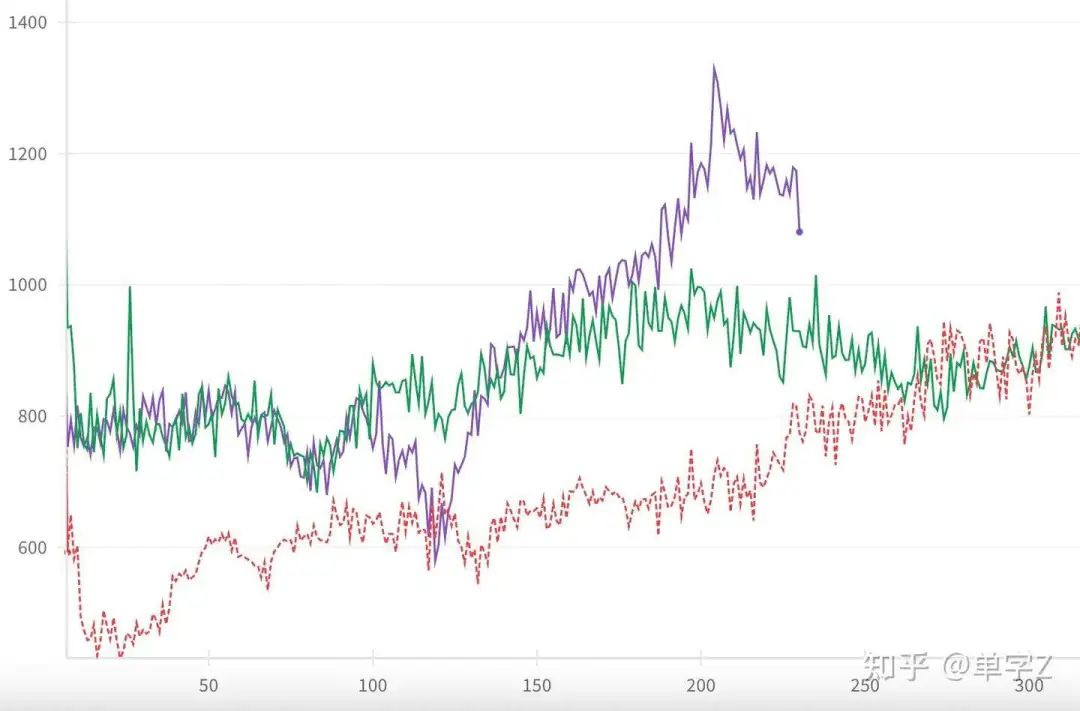
2.反思与正确反思是逐步增加的（这个在7b模型上的增速缓慢），lens也随之增加，eval的效果也在逐渐变好

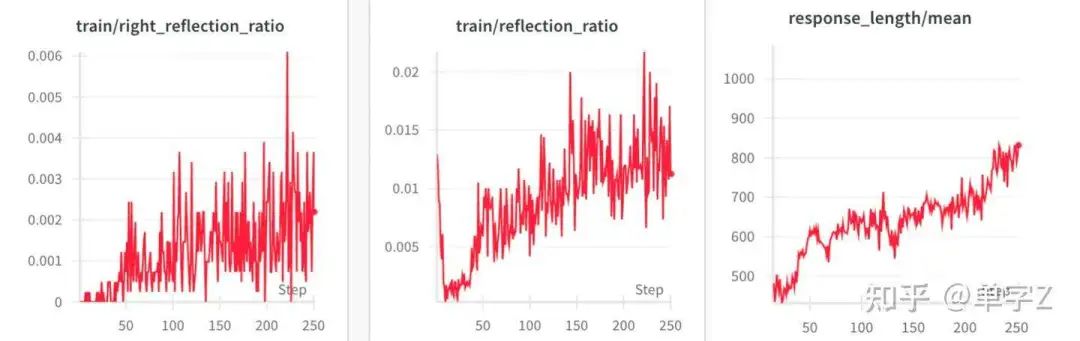
3.大temperature更有助于反思出现，与反思行为的进一步增加，模型的行为是先出现大量无效反思的探索，然后逐渐通过rl学习到有效反思

4.gbz调大是必须的

5.课程学习会有较大收益

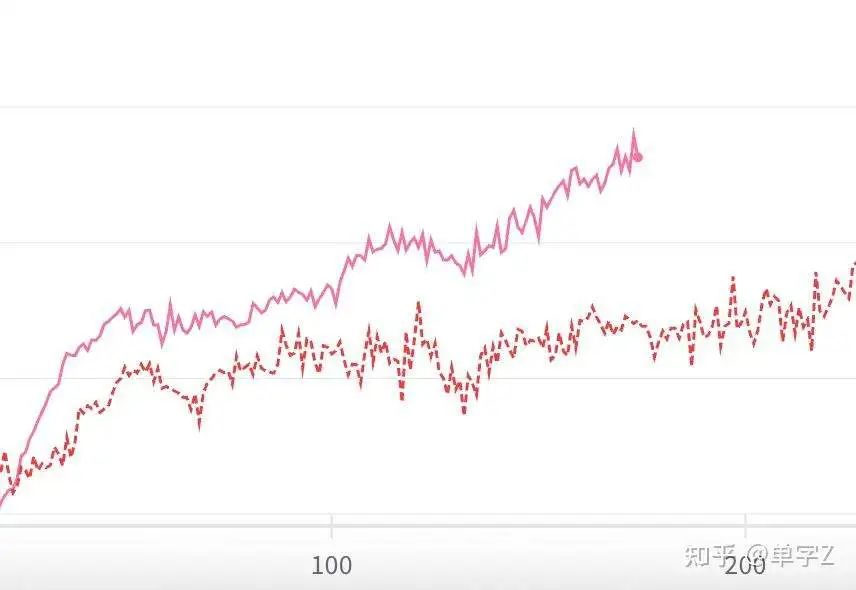
最终的scaling 曲线

待更新，训练比较慢，慢慢等，框架还有许多可以优化的点

目测结论会和r1中的一样，rl zero不如纯蒸馏