

论文题目:Soft Reasoning: Navigating Solution Spaces in Large Language Models through Controlled Embedding Exploration
论文链接:https://arxiv.org/pdf/2505.24688
代码链接:https://github.com/alickzhu/Soft-Reasoning/
本文被ICML 2025收录为spotlight,作者祝清麟为伦敦国王学院(King’s College London)在读博士生
研究背景与核心问题
大型语言模型(LLMs)在多种推理任务中表现优异,但在处理复杂推理任务(例如数学推理)时仍面临显著挑战。现有方法通常通过增加采样的多样性或引入启发式策略来提升推理能力,但这些方法往往难以有效平衡“探索”与“利用”,导致推理效率低或结果不够精确。
本文从一个关键现象出发:即推理过程极大程度上受到首个 token 的影响。我们认为,传统仅依赖从候选词表中选择 token 的方式,未能充分挖掘大模型中庞大参数所蕴含的表达多样性。因此,使用具有大范数(Norm)的连续向量来替代首个离散 Token的词嵌入。由于后续生成过程采用贪心搜索,每个不同的连续向量将对应唯一的生成文本和验证结果,从而在连续向量、生成文本与验证结果之间建立了可优化的一一对应关系。我们进一步将验证结果作为奖励信号,直接优化首个 token 对应的连续向量,以生成奖励更高的文本,从而显著提升推理性能。
该方法的核心优势在于:相比传统基于温度的采样策略,我们能够高效地重复采样那些生成概率虽低、但验证结果奖励较高的答案。在传统温度采样中,此类答案往往需要大量随机尝试才能捕获;而在本方法中,一旦定位到此类解,其在优化过程中将被频繁采样并持续贡献,显著提高优化效率与推理质量。
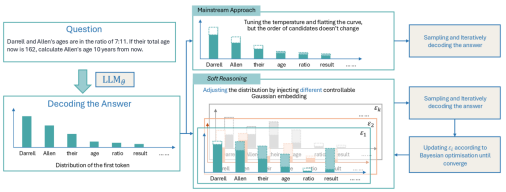
传统温度缩放 vs 嵌入扰动的概率分布对比
具体来说,传统方法(如温度缩放、多路径采样)存在两大缺陷:
盲目性:温度缩放(Temperature Scaling)均匀提升低概率token权重,经常引入噪声而非有效探索。
低效性:基于提示的搜索(如Tree of Thoughts)依赖语言描述,未直接优化内部隐藏层表示,经常导致低效的搜索。
为了应对这些挑战,我们提出了软推理(Soft Reasoning),一种基于词嵌入的搜索框架,通过优化首个生成Token的词嵌入来引导推理生成,该方法的特点是
1.词嵌入扰动:通过对首个生成Token的词嵌入叠加一个可控高斯噪音,从而调整生成token的概率分布,使得生成过程更为灵活,且比温度调节更具可控性,可以直接生成那些低概率的答案。
2.贝叶斯优化:将贝叶斯优化应用于受控扰动的嵌入,以验证器反馈为依据,通过期望改善(Expected Improvement)引导搜索,优化推理路径的选择。
3.无需额外验证器:该方法无需外部验证器,通过内在优化即可提高生成质量,具有计算开销小且无须特定模型参数的优势。
与传统的温度调节或启发式方法不同,我们的方法通过优化首个Token的词嵌入,精确地控制推理过程的方向,避免了盲目增加多样性所带来的噪声和低效问题。
方法
Soft Reasoning框架包含三个主要模块,包括嵌入扰动(Embedding Perturbation),验证器引导的目标函数(Verifier-Guided Objective),以及嵌入空间中的贝叶斯优化流程
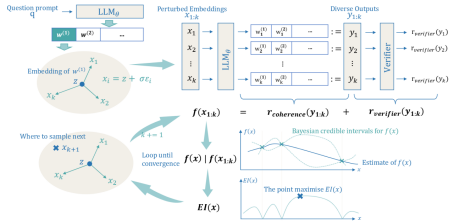
Soft Reasoning 算法流程图
1. 嵌入扰动(Embedding Perturbation)
核心思想:通过高斯噪声扰动首个生成token的词嵌入,生成多样化候选解。
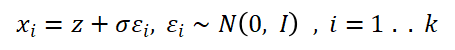
关键步骤:
a.初始嵌入:z为模型生成的首个Token的原始词嵌入
b.可控扰动:通过标准差σ控制噪声强度,生成k个候选嵌入{x_i};这里我们设置的默认标准差是1,这个标准差显著高于大多数语言模型的token标准差。也就是说整个噪声强度将极大改变第一个token的范数,从而起到显著影响结果的作用。
c.确定性生成:对每个x_i,使用贪婪解码生成完整序列y_i,确保x_i和y_i一一映射。
这一策略的优势在于(对比温度缩放):避免全局概率分布扁平化,定向调整低概率词元
2. 验证器引导的目标函数(Verifier-Guided Objective)
目标函数设计:
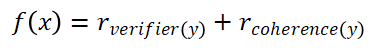
组件解析:
1.验证器得分r_verifier(y):使用同模型作为验证器,判断生成答案y是否与验证器答案y_v一致。
2.连贯性得分r_coherence(y):计算生成序列的token对数概率之和,评估语义流畅性。
这一策略的出发点在于:在上一步的扰动生成过程中,有可能过多的聚焦于低概率词的解码。为了平衡这种倾向性对于语义连贯性的破坏,我们引入的了不同的打分指标来保留高概率区域更连贯的解码结果。并且,同时考虑估计代价(r_verifier(y))和实际代价(r_coherence(y)),也更符合启发式搜索的直觉。
3. 嵌入空间中的贝叶斯优化流程
在本工作中,我们将目标函数视为一个黑盒模型,不对其内部参数进行显式分析或建模,仅将其看作一个能够输出分数,但是具体表达式未知的函数。在问答任务(QA)中,我们将每一个问题都视为一个独立的黑盒,其输出的验证得分会随着我们插入的向量不同而发生变化。借助我们构建的一一映射机制,我们可以在每个问题对应的搜索空间中,寻找一组最优向量,使其生成的答案在验证器中获得最高得分。
为实现这一目标,我们采用了贝叶斯优化算法。选择该方法的主要原因在于:贝叶斯优化是一种专用于黑盒函数极值求解的高效算法,适用于目标函数形式未知、梯度不可用的场景。该方法通过对已有一组采样点的函数值进行建模,利用高斯过程回归预测任意输入处函数值的概率分布。随后,依据该分布构造采集函数,用于衡量每个候选点的探索价值。通过最大化采集函数,我们确定下一个最优采样点,并在多次迭代后,最终返回在所有采样点中获得的最优值,作为目标函数的极大值近似解。
具体操作如下
a.我们将目标函数f(·)视为一个黑盒,并使用高斯过程(Gaussian Process, GP)作为其代理模型,初始化观测批次{(x_i,f(x_i))}_i=1^k
b.在第 t 轮迭代中,根据当前代理模型,使用期望改进(Expected Improvement, EI)作为采集函数,选择下一个查询点:
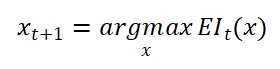
EI 函数能够权衡“探索”(不确定区域)与“利用”(高分区域),自动引导搜索过程向潜在最优区域靠近。
c.对选出的采样点 进行实际评估,获取其真实目标函数值,并将该点加入观测集合。代理模型随之更新,以更准确地反映当前函数走势。
d.重复步骤 2 与步骤 3,直到满足终止条件。终止条件包括当前轮次的 EI 值低于预设阈值(表示模型已收敛),或达到最大迭代轮数。
e.在具体操作过程中,我们选择随机投影策略将高维嵌入降至低维,以缓解高维优化难题。
相比于传统的调整温度进行采样的方法,基于贝叶斯优化的采样中,每次轮采样的结果都会借鉴之前轮次的结果,有针对性的调整相关的参数,使得整个采样过程更加可控且高效
实验验证与关键结果
(1)性能全面提升
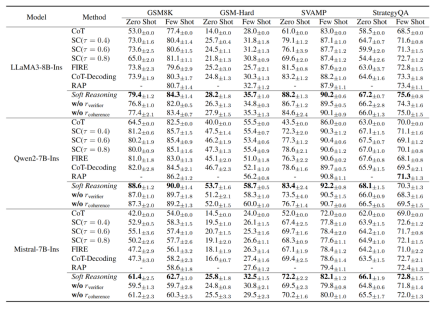
(2) 机制有效性分析:在分析相关实验结果的过程中,我们可以观察到以下现象:
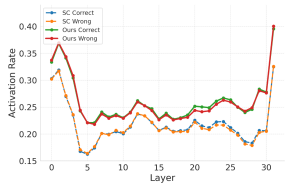
Transformer各层的MLP激活率(采样200次,取生成答案的前五个token)
1.神经元激活多样性:Soft Reasoning使Transformer MLP层激活率提升3-4%,触发更多关键推理路径;
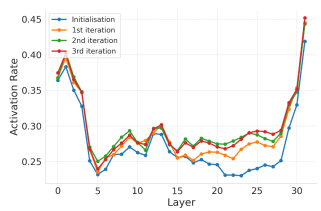
并且,关键神经元激活率随优化轮次逐渐提升
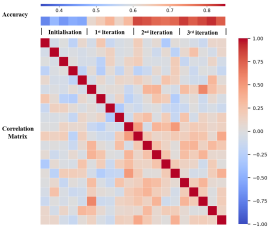
2.贝叶斯优化过程中,随着迭代轮次增加,可控嵌入相关性不断增加,性能不断提升
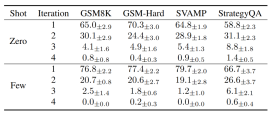
在第 n 次迭代终止的测试样本占比
3.收敛效率:大多任务在前两轮收敛
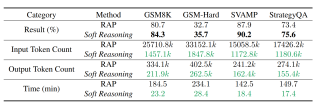
Soft Reasoning与RAP在性能和token消耗方面的对比
4.推理成本:与基于MCTS搜索树的基线RAP相比,提升了推理性能的同时大大降低了推理成本
(文:机器学习算法与自然语言处理)

