©PaperWeekly 原创 · 作者 | 苏剑林
单位 | 科学空间
研究方向 | NLP、神经网络
众所周知,完整训练一次大型 LLM 的成本是昂贵的,这就决定了我们不可能直接在大型 LLM 上反复测试超参数。一个很自然的想法是希望可以在同结构的小模型上仔细搜索超参数,找到最优组合后直接迁移到大模型上。
尽管这个想法很朴素,但要实现它并不平凡,它需要我们了解常见的超参数与模型尺度之间的缩放规律,而 muP 正是这个想法的一个实践。
muP,有时也写 ,全名是 Maximal Update Parametrization,出自论文《Tensor Programs V: Tuning Large Neural Networks via Zero-Shot Hyperparameter Transfer》[1],随着 LLM 训练的普及,它逐渐已经成为了科学炼丹的事实标配之一。

方法大意
在接入主题之前,必须先吐槽一下 muP 原论文写得实在太过晦涩,并且结论的表达也不够清晰,平白增加了不少理解难度,所以接下来笔者尽量以一种(自认为)简明扼要的方式来复现 muP 的结论。
先说结论,muP 主要研究超参数跨模型尺度的迁移规律。这里有几个关键词:
1. 超参数,目前主要指学习率;
2. 模型尺度,目前主要是模型宽度;
3. 这里的核心是“迁移”。
请注意,muP 不研究什么是最优的超参数,只研究最优超参数随着模型尺度的变化规律,所以我们需要在某个小模型上搜索最优的超参数组合,然后迁移到大模型上,这就是 muP 的使用场景和使用方法。
推导 muP 的原理是让模型的前向传播、反向传播、损失增量和特征变化都不随模型尺度的变化而发生明显变化:
1. 具体做法是分析初始化的数量级,然后认为结论可以代表后续优化的规律;
2. 说白了就是假设做好初始化,后面就会自动沿着正确的轨迹走(好的开始是成功的一大半?);
3. 当然也可以给这个假设讲大数定律或中心极限定理的故事,但个人认为非必须。

前向传播
我们从前向传播开始讨论,因为这是相对简单且成熟的部分。首先,考虑线性层 ,其中 。我们用RMS(Root Mean Square)来作为矩阵尺度的指标,例如
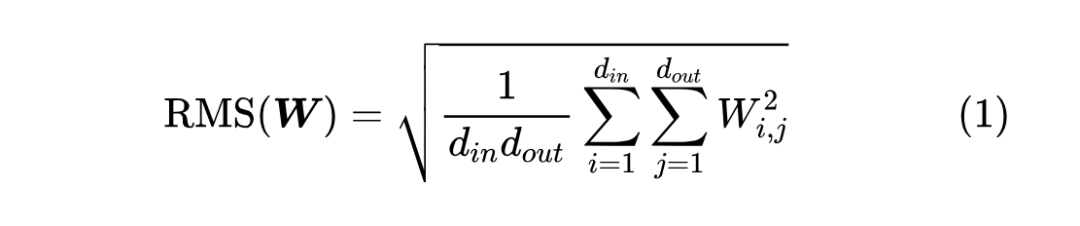
我们知道,要让初始化阶段 的 RMS 跟 的 RMS 大致相等(简称“稳定”),那么 要用:
LeCun 初始化:“均值为 0、方差为 ”的随机初始化。
这已经算是深度学习的基础结论之一,所以不再展开推导,还不大了解的读者可以参考以往的《从几何视角来理解模型参数的初始化策略》[2]、《浅谈Transformer的初始化、参数化与标准化》[3] 等文章。
接着,我们考虑非线性层 ,其中 是 Element-wise 的激活函数。如果还是要维持 的 RMS 跟 的 RMS 近似相等,那么结果会稍有不同,比如 激活时我们得到
Kaiming 初始化:“均值为 0、方差为 ”的随机初始化。
容易看出,Kaiming 初始化跟 LeCun 初始化相比,只是方差相差一个(跟模型尺度无关的)常数 2,可以证明其他激活函数的结果也类似。所以我们可以下一个结论:
fan_in 初始化:要保证前向传播的稳定性,那么应该要用“均值为 0、方差正比于 ”的随机初始化。
这个结论也可以理解为“激活函数的影响是模型尺度无关的”,所以如果我们只想分析模型尺度的效应,那么可以忽略(Element-wise 的)激活函数的存在,由 LeCun 初始化直接得到缩放规律 。

反向传播
现在我们继续分析反向传播(梯度),注意这里约定变量及其梯度具有相同的 shape,那么可以算得
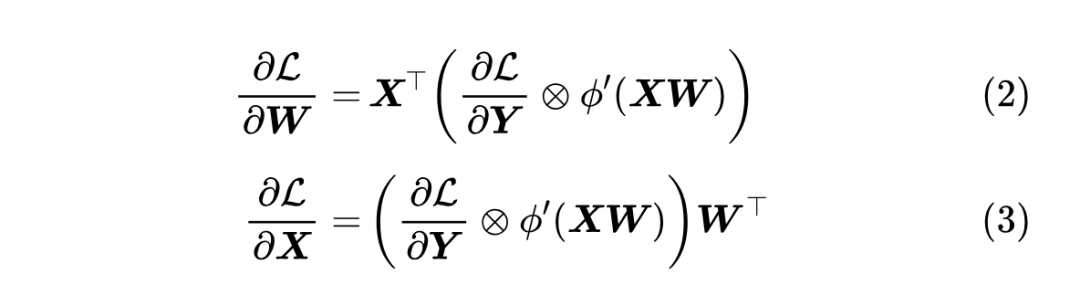
第一个公式是当前层内参数的梯度,第二个公式则是该层往前传播的梯度, 是 Hadamard 积, 是 的导函数。
注意到一个事实:我们常用的激活函数,其导数都可以被一个(尺度无关的)常数给 Bound 住,所以至少在数量级上我们可以写出
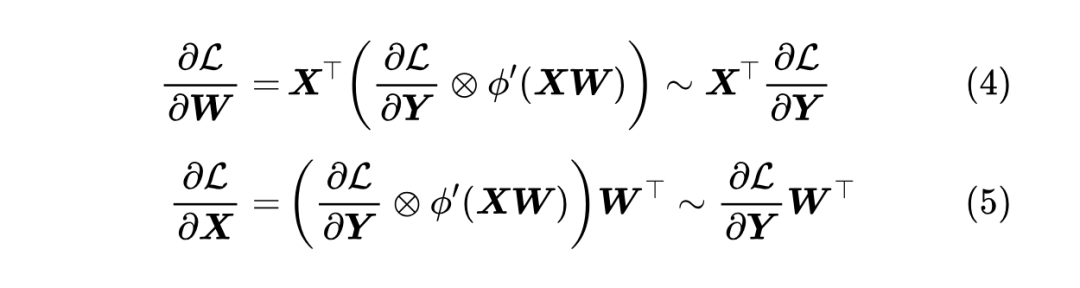
我们先来看第二个公式,跟 相比,它右端乘的矩阵变成了 ,那么按照上一节的结论,如果要保持反向传播的 RMS 稳定性,那么 的初始化就应该是:
fan_out 初始化:“均值为 0、方差为 ”的随机初始化。
当 时,前向传播和反向传播的要求就出现冲突,这时候有人提了一个折中策略:
Xavier 初始化:“均值为 0、方差为 ”的随机初始化。
这也叫“fan_avg 初始化”,因为就是将 和 简单代数平均了一下,其他平均方式也可以考虑,参考《初始化方法中非方阵的维度平均策略思考》[4]。Xavier 初始化看上去同时兼顾了前向和反向,但也可以说两者都没兼顾,更好的办法是设计模型让大部分参数都是方阵,如后面讨论的模型簇(8)。

损失增量
有了前向传播和反向传播的铺垫,我们就可以尝试分析损失函数的增量了。考虑 时损失函数的变化量
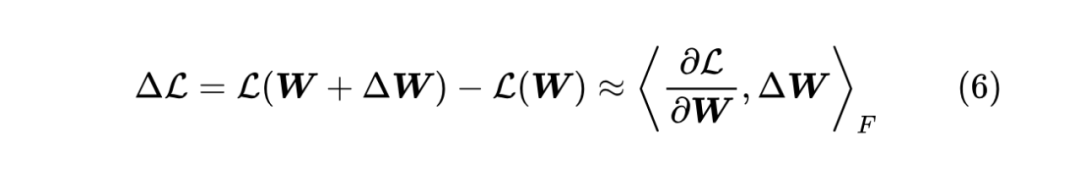
这里的 是 Frobenius 内积,即把矩阵展平成向量后算向量内积。考虑梯度下降 ,这里 自然是学习率,结合式(4),我们有
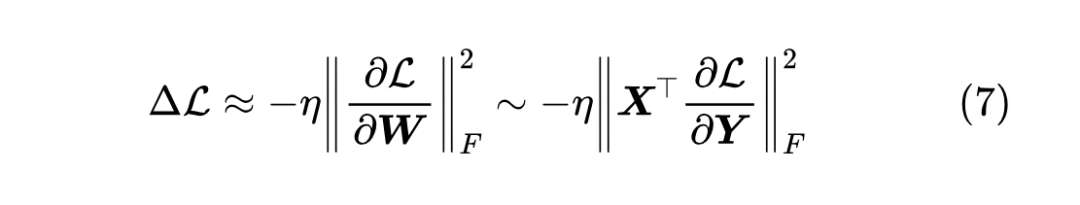
事实上,这个式子已经告诉了我们同一个学习率 不能跨模型尺度使用的原因:
1. 是一个 的矩阵;
2. 是 个数的平方和;
3. 正好是前向和反向的乘积;
4. 如果前向和反向都稳定,那么 每个元素都是 ;
5. 所以 就是 。
第 4 点可能要多加评述一下。 是一个 矩阵, 是一个 矩阵,两者相乘就是 个 维向量对做内积,内积是 项求和,而损失 通常是对样本求平均(即包含了除以 操作),所以如果 和 都是尺度无关的,那么它们乘起来基本也是尺度无关的【即 RMS 都是 】。
最后的结论表明,如果我们直接将小模型的学习率用于大模型,那么对于足够大的模型,它的每一步损失增量就会随着参数尺度(即 )的变大而爆炸,这意味着没法复制小模型的收敛过程,甚至可能因为步子迈得太大导致无法收敛。
此时大家可能想到的一个做法是让 来缩放 ,事实上这个想法已经跟上了 muP 的思路,但实际场景中由于前面说的前向和反向的不兼容性,导致第 4 点“如果前向和反向都稳定,那么 每个元素就是 ”不能总是成立,所以实际情况更为复杂一些。

模型假设
现在让我们考虑一个更接近实践的场景。我们的任务是训练一个 的模型,其中 是数据决定的,不可改变。开头我们就说了,muP 旨在研究超参数随着模型尺度的缩放规律,所以一切固定不变的量,都相当于是常数或者说 ,比如初始化方差为 ,等价于说初始化方差为 。
我们可以改变的是模型的架构、参数量等部分,但 muP 主要考虑宽度的规律,所以我们把模型的架构定一下。这里主要考虑的模型簇是:
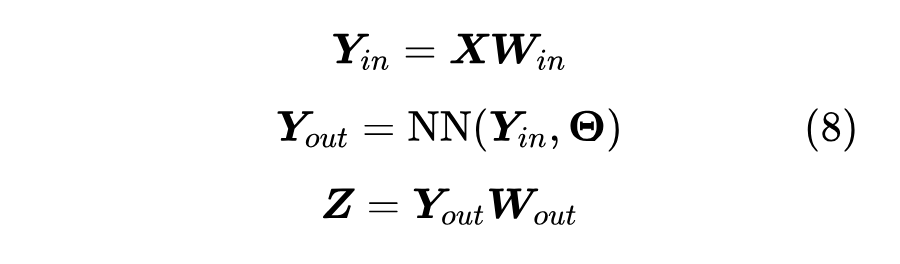
其中:
1. (带上了 batch size);
2. ;
3. 是任意 的神经网络;
4. 这里 其实就是我们常说的 hidden size;
5. 我们可以随意调大 ,来提升模型的参数量和潜力;
6. muP 就是想研究超参数关于 的变化规律。
更具体一点,这里我们考虑的 是 K 层 MLP:
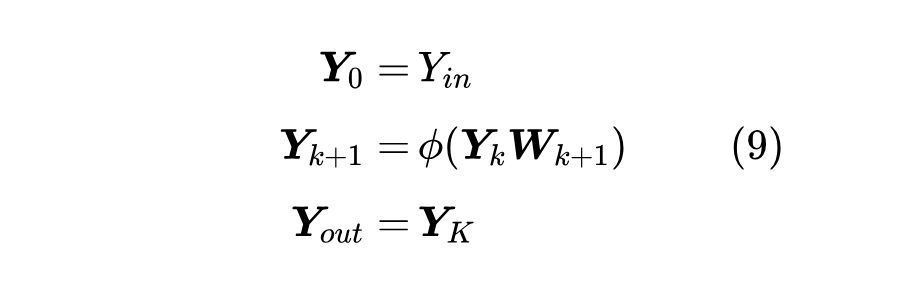
这里 ,,即都是 的方阵,全都用 fan_in 初始化(等价地,也是 fan_out 初始化)。
补充一下,这里约定所有参数矩阵都是 方阵,纯粹是为了简化分析,并不是强制要求。因为这里真正的目的是假设 的参数里没有尺度无关的形状,比如不允许 这样的形状,因为 64 是一个常数,但 这样的形状是允许的,因为你不管 fan_in、fan_out 或 fan_avg 初始化,方差都是正比于 。

组装起来
确立后具体模型后,我们就可以把前面的结论都组装起来了。要更新的参数分为 三部分,分别求梯度:
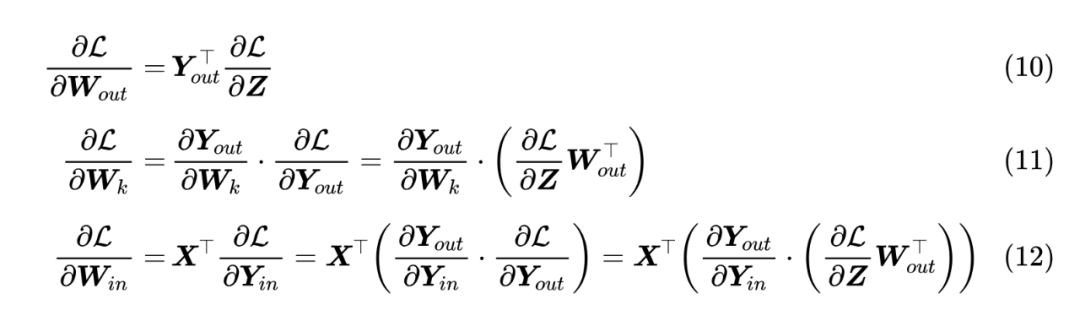
这里的 运算需要稍微解释一下: 都是一个矩阵,所以 原则上是一个四阶张量,链式法则 实际是高阶张量的乘法,但这里不打算展开介绍了,所以简单用一个 代替,读者只需要知道它是矩阵乘法的一般推广就行。
现在来观察规律:
1. 三个式子都有 ;
2. 后两式都有 ;
3. 里都是方阵, 和 都是稳定的【RMS 是 】;
4. 如果 也用 fan_in 初始化,那么 也是稳定的;
5. 要想 稳定,那么初始化方差是 ,但 是尺度无关的,相当于常数。
这样一来:
1. 的 RMS 是 , 是 个数平方和,所以大小是 ,别忘了 是常数,所以实际上就是 ,于是为了得到 的 ,它的学习率要满足 ;
2. 是 个数求和, 和 的 RMS 都是 ,我们直接将 的初始化方差设为 ,那么 的 RMS 就是 ,平方求和后就正好是 ,因此学习率不用变化;
3. 此时 的 RMS 也是 ,但 只是 个数平方和,所以结果是 的,为了得到 的 ,学习率反而需要放大 倍来抵消这个影响,即 。

特征变化
以上结果是没有问题的,但仔细思考我们会发现推导过程的一个问题:上面的第 2、3 点,都建立在“我们直接将 的初始化方差设为 ”这个设置上,然而这个设置目前来说并没有直接的依据。如果不对此进一步解释,那么推导过程还是不够完备的。
事实上,单看 这个要求的话,确实是无法排除其他选择的可能性的,比如 的初始化方差设为 ,此时 的 RMS 是 ,平方求和后是 ,那么只要学习率 同样可以实现 。因此,为了解释 “ 的初始化方差设为 ”的必要性,那么就需要引入新的条件。
损失函数 是模型的一个宏观指标,或者说外部指标,单看它的变化已经不足以解释全部结果了,那么就需要细化到模型内部了。具体来说,我们希望模型每一层的输出(通常也称为特征,有时也称激活值)变化量也具有尺度不变性。比如线性层 ,参数 带来的输出变化是
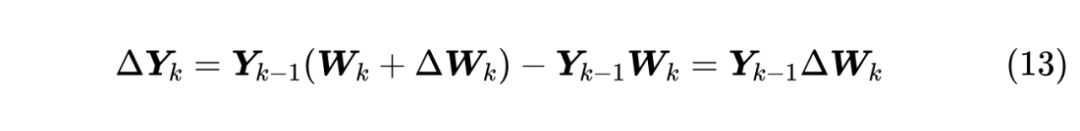
注意 ,所以 就是 个 维向量对的内积。
注意这里 是精心设计的更新量,它不大可能跟初始化那样跟 是独立的,所以“ 维向量对的内积”更有可能是 ( 维内积共有 项求和),因此如果 的 RMS 是 ,那么可以认为 的 RMS 将是 。
于是,为了让 的 RMS 是 ,我们得到了对 的一个额外要求:
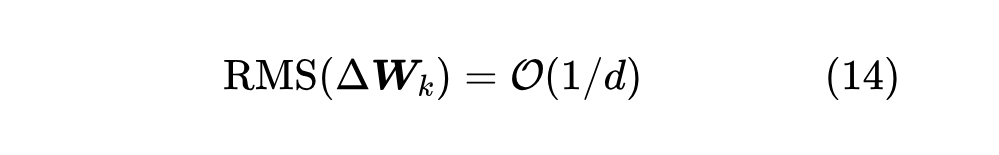
结合 和 ,我们就可以得到 “ 的初始化方差设为 ”的结果。
(注:这一节依赖于 @Chenyu Zheng 的指点,非常感谢!)

Adam 版本
以上就是 SGD 的 muP,对于 Adam,我们通常用 SignSGD 近似做数量级分析:
1. ;
2. ;
3. 这里的 指每个元素取绝对值然后求和。
关于 SignSGD 近似本身,读者还可以参考《当Batch Size增大时,学习率该如何随之变化?》、《Adam的epsilon如何影响学习率的Scaling Law?》等文章,这里也不展开讨论了。总而言之,SignSGD 是分析 Adam 相关缩放规律时一个常用的近似方式。
现在可以模仿 SGD 的过程进行分析:
1. 的 RMS 是 , 是 个数求和,大小是 ,所以它的学习率要满足 来抵消尺度影响;
2. 是 个数求和, 和 的 RMS 都是 ,我们将 的初始方差设为 ,那么 的 RMS 就是 , 个数求和后是 ,所以学习率按照 变换来抵消尺度影响;
3. 此时 的 RMS 也是 ,但 只是 个数求和,所以它已经是 ,从而学习率不用随尺度改变。
(注:读者可以自行检查一下式(14)是满足的。)

Muon 版本
接下来自然少不了 Muon 的分析。对于 Muon 本身,我们已经在《Muon优化器赏析:从向量到矩阵的本质跨越》、《Muon续集:为什么我们选择尝试Muon?》[5] 做了详细介绍,这里不再重复。跟 Adam 用 SignSGD 类似,我们用 MSignSGD 来近似 Muon:
1. ;
2. (证明见《Muon优化器赏析:从向量到矩阵的本质跨越》);
3. 这里的 指 Nuclear 范数 [6],是矩阵的所有奇异值之和;
4. Nuclear 范数并不好算,但 F 范数好算,它等于矩阵的所有奇异值的平方和的平方根;
5. 我们用 范数作为 Nuclear 范数近似,因此 ;
6. 范数又等于矩阵的所有元素的平方和的平方根。
那么可以开始分析过程:
1. 的 RMS 是 ,所以 大小是 ,要消除尺度的影响,那么它的学习率要满足 ;
2. 是 个数的平方和的平方根, 和 的 RMS 都是 ,我们将 的初始方差设为 ,那么 的 RMS 就是 ,平方和后再平方根,结果是 ,所以学习率不用变;
3. 此时 的 RMS 也是 ,但 只是 个数的平方和平方根,所以它是 的,学习率反而需要放大 倍来抵消这个影响,即 。
(注:这里 Muon 的结论是对的,但它不满足条件(14),因为式(14)要细说的话还依赖于一个更新量是 Element-wise 的假设,而 Muon 不符合这个假设,所以实际上不可用。这里没有仔细展开相关讨论,而是直接沿用了“ 的初始化方差设为 ”的结论,回避了式(14)。)

结论汇总
将上述结论汇总在一起是:
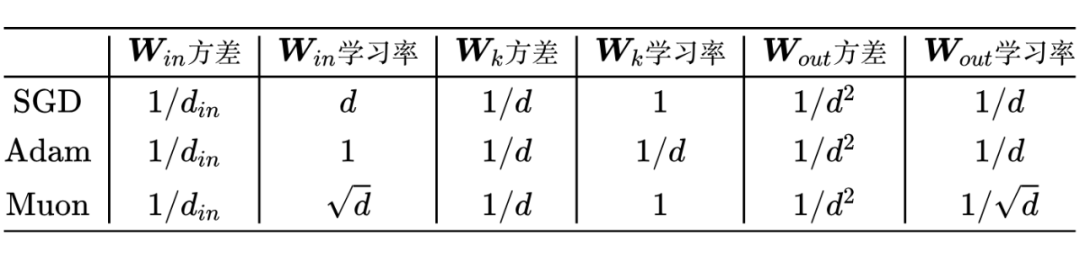
这里的 指的是除 外的所有参数,还有要强调的是,这里的关系都是“正比于”而不是“等于”。另外实践中可以根据具体需求稍作变化,比如实际我们用 Muon 时, 和 的优化通常不用 Muon 而是用 Adam,这将导致两个变化:
1. ;
2. 不变。
如果结合我们在《Muon is Scalable for LLM Training》[7] 所提的 Adujst LR 的话,那么学习率要多乘一个 , 是参数矩阵的形状,我们已经假设了 部分的参数总等比例缩放,所以 。因此,如果要抵消 Adujst LR 带来的尺度影响,那么就需要
3. 。

文章小结
本文以尽可能简明清晰的方式介绍了 muP(Maximal Update Parametrization),这是旨在研究超参数跨模型尺度的迁移规律的工作。基于 muP,我们可以在小模型上以相对较小的成本仔细搜索超参数(这里主要是学习率和初始化),然后迁移到大模型上,降低大模型的炼丹成本。
客观来讲,这里的介绍和分析还比较初步,比如没有考虑 Bias 项、没有评估结论在 MLP 以外架构的通用性、也没有仔细考虑 Normalization 和残差的作用等。
没有考虑 Bias 项这个单纯是偷懒,权当留给读者的习题了;至于不同架构下的 muP,一般分析起来比较麻烦,但由于神经网络的相似性,结论大致上是相同的,我们可以不加证明地用着。
个人认为比较关键的改进点是 Normalization 和残差的影响,尤其是 Normalization,它使得不依赖特殊的初始化就可以稳定前向传播,带来了更大的自由度和可能性。
当然,这些都留给后续分析了。
(文:PaperWeekly)