强化学习基于奖励最大化假设,所有的算法都是建立在得到一个最大的期望奖励的基础上。
首先来明晰两个概念:
On-Policy: 训练数据由需要训练的策略本身通过与环境的互动产生,用自己产生的数据来进行训练(可以理解为需要实时互动)
Off-Policy: 训练数据预先收集好(人工或者其它策略产生),策略直接通过这些数据进行学习。
PPO, GRPO,DAPO都是On-Policy的策略。这些On-Policy的策略一般由四个关键组件组成训练的pipeline:
-
• Actor: 产生动作的策略 -
• Critic: 评估动作或状态的价值的网络 -
• Reward Model:对状态转移给出即时的奖励的模型或者函数 -
• Reference Model: 参考策略,这是为了防止在训练过程中,策略网络在不断的更新后,相对于原始策略偏移地太远。(避免它训歪了)
从PPO出发,捋清强化学习训练的思路
Policy gradient optimization
基于奖励假设,我们希望得到一个能够最大化奖励期望的策略,这个目标可以写成:
而奖励来自于轨迹上的每一个动作的即时奖励,于是,这个目标可以写成:
这里的 代表一系列的动作状态轨迹,也就是所谓的sasa。
而
这里的状态转移由当前状态和选择的动作决定,也就是:
那么,一条轨迹的整体概率分布可以写成:
对于policy gradient的方法来说,我们希望通过梯度上升的方式最大化轨迹得到的奖励,也就是最大化我们的目标函数。梯度上升的更新公式可以写为:
那么问题来了,如何计算目标函数的梯度呢,这个目标函数涉及一轮迭代中轨迹上的所有点,直接去计算或者估算都具有很大的困难,而且还有由环境和策略共同决定的状态转移项,这么多项揉在一起似乎无法求解。但是呢,要不说数学家是天才呢,它可以由一系列简单的变换变为只与策略有关的项。先来对这个目标函数的梯度进行一个简单的推导:
那么上述目标函数的梯度转变为了一个对轨迹转移与奖励函数的积分,采用log函数的导数变换技巧,上式可以变成:
由于 代表路径,所以这里的这个积分可以再写回成为一个期望:
由于我们知道 ,那么对这个方程取log对 求导,可以得到:
这个变换很巧妙,如果不取log的话,就要处理这里的连乘状态转移,而这个往往是一个跟环境有关的不定项。
那么目标函数的导数变成:
那么现在就得到了一个只与策略和奖励有关的式子,我们可以对此进行计算,但是显然不可能对能够采样所有轨迹来进行梯度计算,在很多场景下要不轨迹无限要不穷举所需算力太大,所以我们只能对它进行估算。而进行采样估算,就要请出大名鼎鼎的蒙特卡洛算法了。蒙特卡洛算法其实就是通过局部采样来估计整体的方法,那么我们可以采样一部分轨迹,得到
那么这个 就可以用来做期望的估计值,也就是策略梯度的估计值。
Reinforce 算法
根据上面的策略梯度优化的推导基础,我们可以开始介绍经典的Reinforce算法,这个算法就是简单的梯度策略优化的应用。
那么现在有一个需要优化的策略网络 ,它会根据当前状态 输出一个动作概率分布 ,用于指导当前应该采用怎样的动作。
有了策略网络以后就可以开始在环境中采集动作轨迹 ,这些动作轨迹用于计算策略更新的梯度(上述蒙特卡洛法)。
当收集到了足够多的轨迹以后,采用这个蒙特卡洛估计法来计算策略梯度:
然后根据梯度进行策略更新:
反复进行采样然后计算梯度然后更新网络,直到你的策略网络拟合。
这就是经典的Reinforce算法。
评估一下这个算法:
这是一个Model-free的算法,因为只涉及对策略网络本身输出采样,而不涉及由环境决定的状态转移过程。
但是呢,由于需要进行采样估计,虽然蒙特卡洛法是策略梯度的无偏估计,但是如果样本太少的话,得到的方差可能就会很大,这不利于训练的稳定性。其实这也是策略梯度优化方法的固有缺陷,如果要学习的行为足够复杂(采样的轨迹太长)或者策略网络过大,那么要进行的采样和计算量也是非常大的,不然梯度估计的方差就会变得很大。
那么有没有减小方差的方法呢?有的兄弟,包有的
Focus only on the future
回顾一下我们目前介绍的梯度策略优化算法,每一步的估计都乘上了从轨迹开始到结束的所有奖励,想一想真的需要吗?我第10步的时候去做下一步决策的时候,过去9步的奖励还应该被考虑进来吗?什么?你说不需要,我也说不需要,从因果的角度来看压根不需要之前的奖励!那么我们可以改写一下策略梯度的数学表达式,变为:
这样计算每一个轨迹点上的梯度时,就把过去的奖励给过滤掉了,一定程度上减小了方差。这里的 一般称为rewards-to-go,或者称为状态-动作价值(对应DQN算法中的Q值)
引入一个奖励基线
引入一个基线可以有效减小方差(例如数据在基线上下跳动,那么对所有的数据减去这个基线的话,数据整体的方差就会有效减小,大概想象一下就可以)
这里的b就是引入的基线,这个基线常常是用一个价值模型评估当前状态的价值,即
优势函数
引入了rewards-to-go和奖励基线以后, 这一项我们称为优势函数,它的意义是当前状态下选择某个动作的价值相较于这个状态下的平均价值的好坏。通常前一项称为Q-function,后一项是vaule-estimate. 那么把这一项可以定义为:
那么现在的策略梯度估计可以改写为:
从rewards-to-go到优势函数,目前做的一系列工作都是为了减少方差。接下来开始介绍PPO算法了
Generalized Advantage estimation(GAE)
对于价值函数,我们有
那么优势函数可以写为:
同样的,如果再迭代一步,可以得到
重复迭代可以得到
我们定义每一步的TD error为: ,为了便于观察,可以再写一项
那么我们把它代入回多步估计优势函数的式子中去,可以发现:
以上都是通过采样去对优势函数进行估计的可行公式。
那么GAE就是对多步估计优势函数的求和:
这里求和对于每一项还添加了一项衰减因子
把它展开来,就可以得到:
如果我们采集K步的话,那么通过等比数列求和公式,我们得到:
当 ,上式实际上变为
那么
把 作为GAE, 那么就得到
这个式子也可以写成一个递归的形式,即:
以上的所有推导过程中,都有
可以取边界值对这个衰减因子进行一个简单的分析:
时
Proximal Policy Optimization
接下来就是著名的PPO算法啦。PPO需要训练两个模型,一个是策略网络,一个是价值网络(标准的Actor-critic结构)
我们从它的目标函数来分析,首先对于策略网络
这里 就是前文提到的GAE,这里还有一个clip项,是为了防止策略更新过大。
对于价值模型:
这就是很简单的平方损失。
然后还有一个所谓的熵损失,这是用来鼓励探索的
那么总体损失就是:
当然,这里的损失其实完全可以自己设计,但是一般遵循这里的clip原则,因为ppo的核心就是不能让模型训练参数更新过大,否则就会越训练越偏。这里还有个与ref model的KL散度项,也是为了维持模型不要偏太远,即在目标函数中添加上 。
举个例子
公式太多不想看?那就从例子出发来捋一下强化学习的过程
例如使用PPO去训练一个大语言模型:
训练过程中会策略会有两个状态,一个是用于产生采样轨迹的 ,它在产生token prediction的过程中,参数保持不变,而另外一个就是 ,它用于梯度更新。而每轮轮采样结束并更新完梯度以后,
一步一步来的话,就是:
-
• 准备prompt,把它投喂给 -
• 根据prompt生成回答,每个回答包含多个token,而我们训练就是作用在这些token生成的过程中。 -
• 在生成过程中,对于每个生成的token,都记录: (这个语境下就是模型生成当前token前的context), (这个语境下就是模型生成的toekn,以及生成它的log 概率) , 以及对应的 ,这部分用于计算优势
一般来说,强化学习训练llm时,都是用奖励模型或者奖励函数对模型生成的整体回答给一个奖励,然后把这个奖励复制或者平分给每个token,然后用它来计算优势值
然后根据ppo的目标函数来计算梯度啦,计算完一个批次的数据的梯度以后就可以用来更新网络,直到它拟合。
这里插一下DPO
DPO(Direct Preference Optimization)
从PPO的目标函数出发,
这个最大化目标可以改写成最小化目标:
这个目标接着可以写成
最后得到
那么对于分母,可以把它构造成一个概率分布,
其中
那么上面的目标函数可以写为:
即
由于 与 无关,计算梯度的时候用不上,所以可以直接忽略
即
我们知道KL散度总是非负的,而且只有当两个分布完全一样时,它才能达到最小值0,也就是说,PPO的优化目标可以等效于让模型的输出分布 趋近与 一样。
而 ,如果奖励模型的参数保持不变,那它就是我们需要的最优解。
也就是说,我们训练出一个最优奖励模型的时候,实际上它已经给出最优的策略网络。那么也就是说,训练奖励模型和训练策略网络实际上是等价的。那这就告诉我们,像之前的先训练奖励模型,然后通过奖励模型再来训练策略模型的这个范式,实际上并不需要先显式训练出一个奖励模型,而是可以直接用策略模型代替奖励模型去进行训练,从而得到我们最终需要的对齐模型。这两种方法在数学上是完全等价的。所以DPO就绕过了online强化学习,直接用策略网络代替奖励模型去进行训练,从而达到同样的目的。
从上面的最优解变换可以得到:
就有
这里奖励模型就完全可以用策略模型进行替代。
那么来看一下我们一般是如何来训练reward model的,一般来说,训练reward model有两种方法。第一种是采集LLM的两个回答,构造偏好对,来训练奖励模型给正样本更高的分数,负样本更低的分数。它的数据组织形式是: 。
第二种是采集多个回答 ,
两两配对的模式被称为BT model(Bradley-Terry)
BT模型定义的对于两两匹配训练目标是: ,这里 可以理解为y的得分,
那么把它代入我们的奖励模型的目标函数中有:
这里的D就是采集的偏好数据集。之前推导DPO的时候,我们有
那么它代入奖励模型的目标函数中去有:
那么这里就成功把训练奖励模型,改成了直接训练策略模型,从而绕过了训练奖励模型的过程,那么后面的online 强化学习过程也就不需要了,这就是所谓的直接偏好训练。
其实DPO弯弯绕绕这么多,实际上执行起来很简单,几乎就是SFT,以上的公式推导,是为了说明DPO的训练目标在数学上等价于PPO的强化学习训练目标,从而说明PPO可以做成的事,DPO按道理也应该可以做成。
(这里给一些大白话的insight,DPO首先给出了PPO训练最优状态下策略网络与奖励网络的关系,也就是说如果满足了这个关系,PPO的强化学习这一步都不用训练了。那么我们现在假定它满足这个关系了,那么我们还差一个问题,就是奖励模型哪里来的?它是经过reward model的训练过程得来的。而如果满足这个关系,我们不再需要把奖励模型显式地训练出来,而是直接把策略网络代入奖励模型的训练过程。那么这个过程中,奖励模型的目标通过策略网络得到了实现,也就是说,训练奖励模型的过程,使得了这个关系得到了拟合式成立,从而不再需要真正的强化学习训练。)
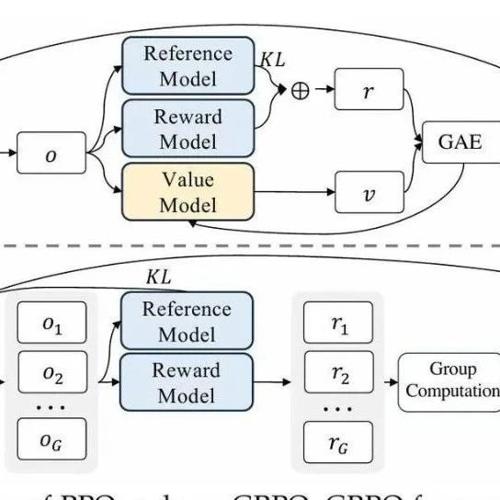
GRPO
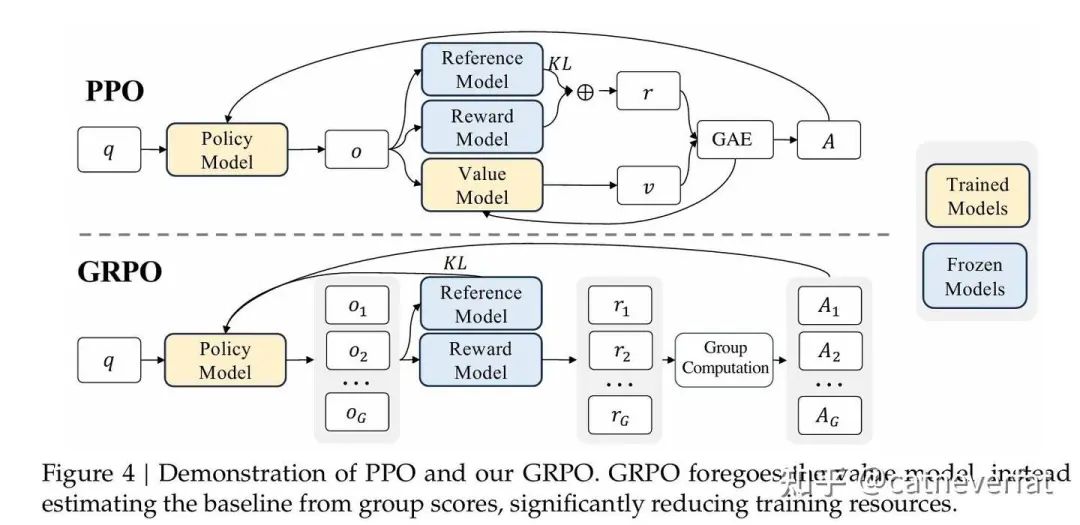
GRPO的目标函数为:
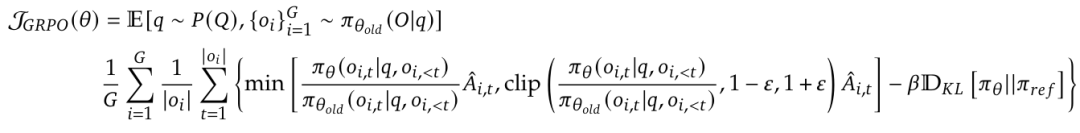
其实主要的就是把GAE Advantage估计改为了组间相对优势估计,
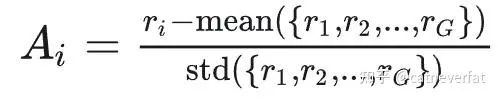
那么这样一改,就不需要value model了,从而减少了训练开销。
GRPO的训练伪代码为:

DAPO
DAPO的目标函数是:

这是字节新发布的基于GRPO优化的一个算法,主要做了以下四个优化:

它第一个clip higher呢意思是对clip的两个边界分别设置不同的 来控制,分别指代为:来控制。而在这里设置为一个相对较大的值。出发点呢是希望鼓励探索,因为概率较小的token预测和概率较大的token预测所受到的clip的影响是不同的,比如等于0.01和0.9时,如果,那么更新的最大允许概率就会是0.012和1.08,那么实际上低概率的token就会长时间难以得到选择。所以对上界给一个更大的来鼓励探索。而下界 保持一个较小值,不然的话可能很多token更新着更新着概率选择就变成0了。
第二个动态采样,更像是一种训练上的工程技巧,说的是在训练过程中,模型可能对很多问题都回答的很好,那么这样一来,对同一个批次中的很多问题,模型采样一组回答,可能都会获得最好的奖励,比如1,那么这样一来,每个回答的组间优势都变成了0,那么这样的数据就无法提供有效的梯度供模型训练。所以在训练目标中,加入了这一项
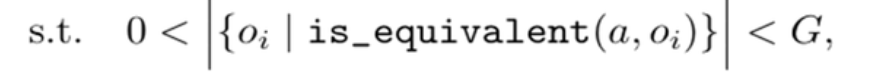
也就是说对于输入的样本持续采样,直到满足这个条件才把这一批数据拿去训练。
第三个是所谓的token level的损失计算。由于GRPO是先对每一条回答基于回答的长度做了一个平均,再对G个回答做一个平均。即:
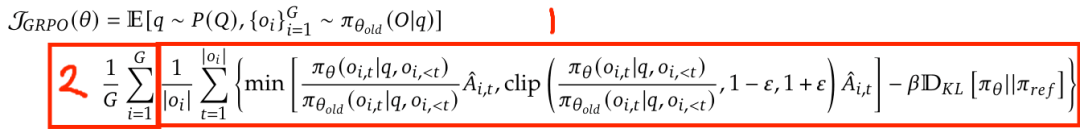
而由于每个回答的长度不一致,这就会导致实际上对多个回答的每个token的loss除以了一个不一样的因子,这会导致一些很长的回答对loss的贡献减小。而在long-COT的训练过程中,我们希望学习到有效的长回答,所以希望对长回答也给相应更大的loss。DAPO把GRPO的这种loss计算方式称为sample-level loss。而DAPO把这个范式改成了:
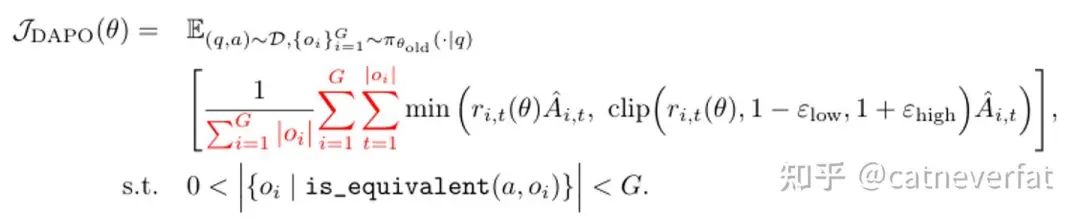
也就是所有的token的loss都施加同样的平均因子,这样对于长回答整体上就给了一个相对更大的loss。
最后一个是说之前训练模型的时候,如果模型生成的回答太长了,超过了限定值,就会被直接阶段。而对于这些被阶段的回答,会施加一个惩罚性的奖励。而这种惩罚性的信号可能又会引入训练噪声,因为可能虽然回答很长,但是却是逻辑上非常正确的回答,那模型就会不知道这个回答到底是好的还是不好的。那DAPO在这里实施了一个跟长度有关的线性奖励:
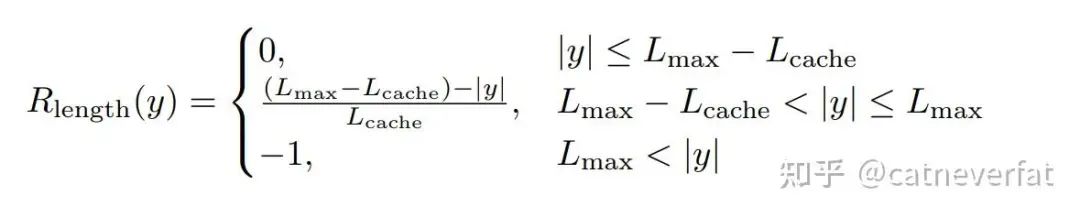
除了上面四个优化技巧以外,DAPO还把KL散度约束给去掉了,理由是:
“However, during training the long-CoT reasoning model, the model distribution can diverge significantly from the initial model, thus this restriction is not necessary. Therefore, we will exclude the KL term from our proposed algorithm. ”就是说long-COT训练过程中,模型本来就是要在较大程度上偏离原始的状态,所以干脆省了用于约束模型更新的KL散度。
DAPO的训练流程伪代码为:

主要参考
https://huggingface.co/blog/NormalUhr/rlhf-pipeline#navigating-the-rlhf-landscape-from-policy-gradients-to-ppo-gae-and-dpo-for-llm-alignment
https://doi.org/10.48550/arXiv.2503.14476
(文:机器学习算法与自然语言处理)