0x0. 前言
最近在SGlang仓库下做了一段时间的开发和学习,对SGLang的一些比较新的Feature也开始有一些了解。这篇文章就是尝试来梳理一下SGLang中Expert Parallel的实现,据我所知SGlang应该是开源推理框架中率先实现Expert Parallel的。我们可以学习一下它是如何实现的,以及它相比于普通的EP主要优化点在哪。SGLang在 https://github.com/sgl-project/sglang/pull/2371 中实现了Expert Parallel,我们从这里看就行。如果对MoE EP不熟悉可以参考 https://zhuanlan.zhihu.com/p/681154742 这篇文章或者阅读 DeepSeek 相关的资料。
0x1. 上层的接口
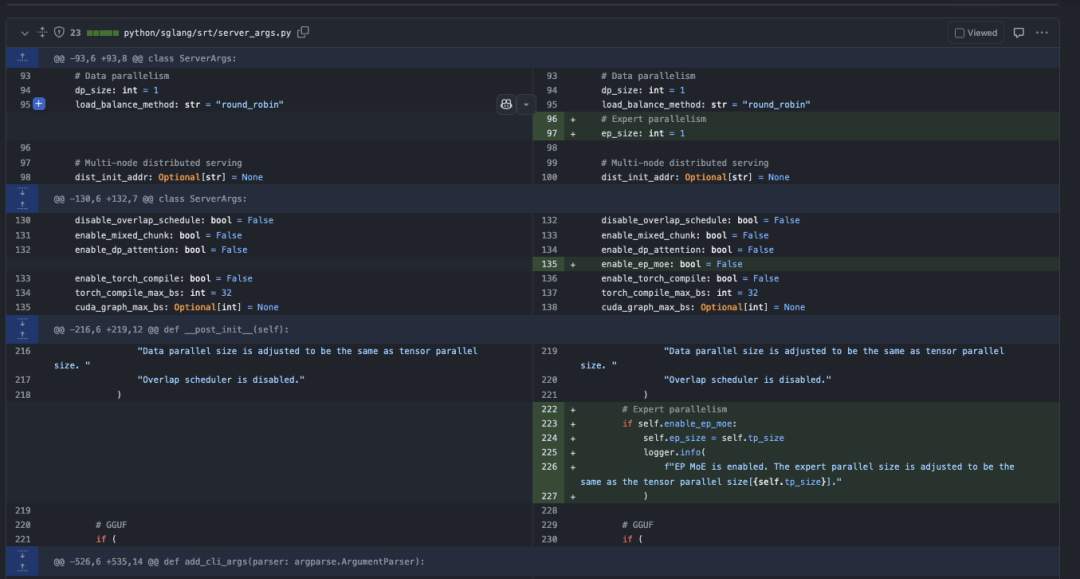
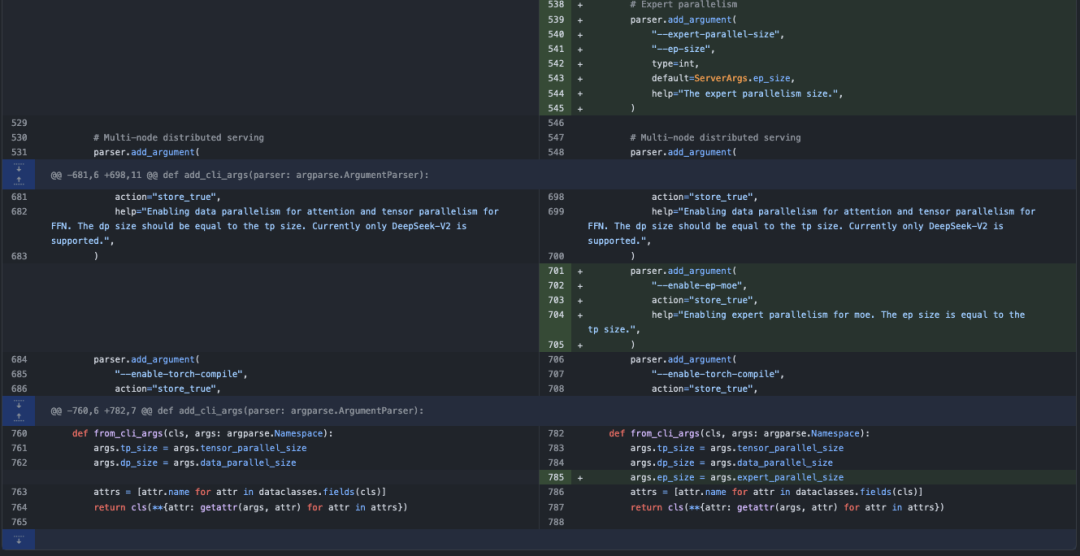
首先我们可以看到server_args.py中的改动,Expert Parallel接管了Tensor Parallel的位置,以Deepseek V3为例子,有256个Expert,现在打开Expert Parallel并且把expert_parallel_size设置为8的话,那么每张卡上分得完整的32个Expert。另外可以看到在初始化参数的时候,如果开启了Expert Paralle会先把expert_parallel_size设置为TP的大小。
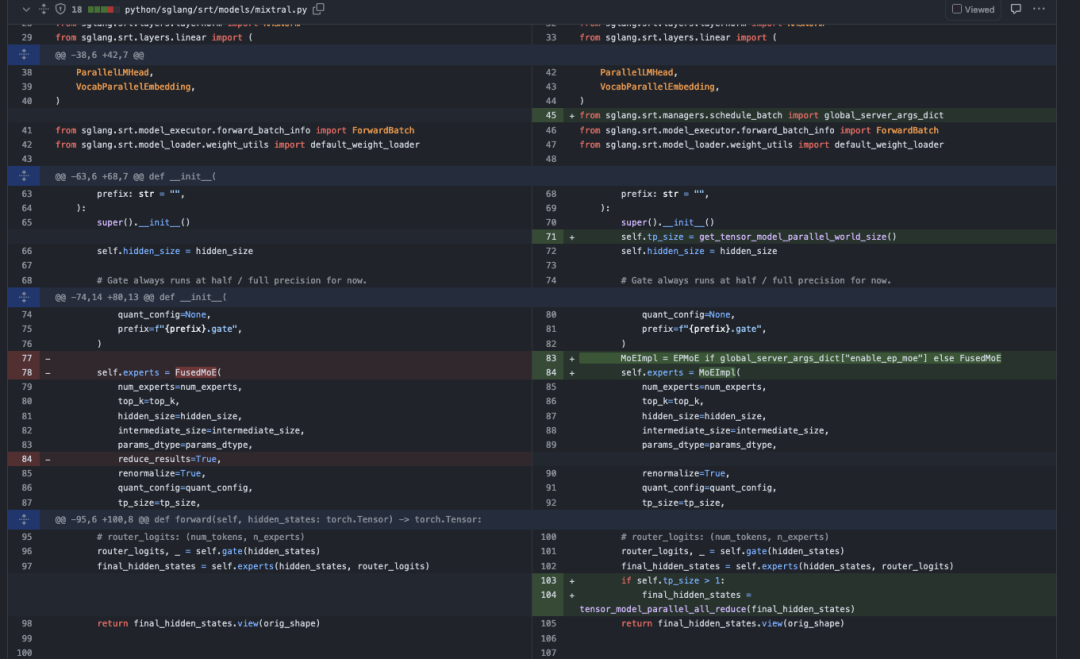
接着看一下Mixtral模型实现上的修改,值得注意的是在调用EPMoE接口的时候没有reduce_results=True,这个参数了,但是在EPMoE计算完成之后对结果调用了tensor_model_parallel_all_reduce 。去掉reduce_results=True,参数比较好理解,在EP中我们没有对Expert的参数做切分,只需要把token分到对应的expert上,做的矩阵乘都是完整的,所以获得的结果也是完整的。为什么要对结果使用tensor_model_parallel_all_reduce?继续读一下代码寻找答案,我在之后的0x4节给出了原因。
上层接口差不多看到这里就可以了,核心实现分成两部分,一部分是EP MoE Layer,一部分是EP MoE的kernel。需要耐心点看这两个。
0x2. SGLang EP MoE Layer实现
文件位置:https://github.com/sgl-project/sglang/blob/main/python/sglang/srt/layers/moe/ep_moe/layer.py
0x2.1 GroupedGemmRunner
首先看到一个用于执行Group GEMM的工具类,首先简单解析一下这个类,降低后续理解的负担。我先添加一下注释:
# 用于执行分组矩阵乘法的Runner类
class GroupedGemmRunner(torch.nn.Module):
# flashinfer的gemm包装器,用于加速计算
flashinfer_gemm_warpper = None
def __init__(self, device, use_flashinfer: bool = False):
"""
初始化GroupedGemmRunner
Args:
device: 运行设备
use_flashinfer: 是否使用flashinfer加速
"""
super().__init__()
self.device = device
self.use_flashinfer = use_flashinfer
if self.use_flashinfer and GroupedGemmRunner.flashinfer_gemm_warpper is None:
GroupedGemmRunner._init_flashinfer_wrapper(device)
@classmethod
def _init_flashinfer_wrapper(cls, device):
"""
初始化flashinfer的gemm包装器
Args:
device: 运行设备
"""
from flashinfer import SegmentGEMMWrapper
# 创建工作空间缓冲区
workspace_buffer = torch.empty(
128 * 1024 * 1024, dtype=torch.int8, device=device
)
cls.flashinfer_gemm_warpper = SegmentGEMMWrapper(workspace_buffer)
# c = a * b
def forward(
self,
a: torch.Tensor, # 输入矩阵a
b: torch.Tensor, # 输入矩阵b
c: torch.Tensor, # 输出矩阵c
batch_size: int, # batch大小
weight_column_major: bool, # 权重是否为列主序
seg_indptr: Optional[torch.Tensor] = None, # 分段指针
weight_indices: Optional[torch.Tensor] = None, # 权重索引
use_fp8_w8a8: bool = False, # 是否使用fp8量化
scale_a: torch.Tensor = None, # a的缩放因子
scale_b: torch.Tensor = None, # b的缩放因子
):
"""执行分组矩阵乘法"""
if self.use_flashinfer:
# TODO: flashinfer
assert False
assert GroupedGemmRunner.flashinfer_gemm_warpper is not None
c = GroupedGemmRunner.flashinfer_gemm_warpper.run(
x=a,
weights=b,
batch_size=batch_size,
weight_column_major=weight_column_major,
seg_indptr=seg_indptr,
weight_indices=weight_indices,
)
else:
# 使用triton实现的分组矩阵乘法
assert weight_column_major == True
c = grouped_gemm_triton(
a,
b,
c,
batch_size,
weight_column_major,
seg_indptr,
weight_indices,
use_fp8_w8a8,
scale_a,
scale_b,
)
return c
总的来说,这个类把两种做Group GEMM的方法抽象了一下,我们可以选择使用CUDA实现的FlashInfer,也可以选择Triton的实现。
0x2.2 EPMoE类
这个类是连接上层的模型实现和底层的EPMoE Kernel的关键组件,我们需要先理解一下这个类的实现。
EPMoE类的定义
class EPMoE(torch.nn.Module):
"""
MoE专家并行实现
Args:
num_experts: 专家总数
top_k: 每个token选择的专家数量
hidden_size: 隐藏层大小
intermediate_size: 中间层大小
params_dtype: 参数数据类型,默认为None使用系统默认类型
renormalize: 是否重新归一化,默认True
use_grouped_topk: 是否使用分组topk,默认False
num_expert_group: 专家组数量,仅在use_grouped_topk=True时使用
topk_group: 每组选择的专家数量,仅在use_grouped_topk=True时使用
quant_config: 量化配置,默认None
tp_size: 张量并行大小,默认None
prefix: 前缀,默认空字符串
correction_bias: 修正偏置,默认None
"""
def __init__(
self,
num_experts: int,
top_k: int,
hidden_size: int,
intermediate_size: int,
params_dtype: Optional[torch.dtype] = None,
renormalize: bool = True,
use_grouped_topk: bool = False,
num_expert_group: Optional[int] = None,
topk_group: Optional[int] = None,
quant_config: Optional[QuantizationConfig] = None,
tp_size: Optional[int] = None,
prefix: str = "",
correction_bias: Optional[torch.Tensor] = None,
):
super().__init__()
# 如果未指定参数类型,使用系统默认类型
if params_dtype is None:
params_dtype = torch.get_default_dtype()
# 设置张量并行相关参数
self.tp_size = (
tp_size if tp_size is not None else get_tensor_model_parallel_world_size()
)
self.tp_rank = get_tensor_model_parallel_rank()
# 设置专家相关参数
self.num_experts = num_experts
assert self.num_experts % self.tp_size == 0 # 确保专家数可以被tp_size整除
self.num_experts_per_partition = self.num_experts // self.tp_size # 每个分区的专家数
self.start_expert_id = self.tp_rank * self.num_experts_per_partition # 当前分区起始专家ID
self.end_expert_id = self.start_expert_id + self.num_experts_per_partition - 1 # 当前分区结束专家ID
# 设置其他参数
self.top_k = top_k
self.intermediate_size = intermediate_size
self.renormalize = renormalize
self.use_grouped_topk = use_grouped_topk
if self.use_grouped_topk:
assert num_expert_group is not None and topk_group is not None
self.num_expert_group = num_expert_group
self.topk_group = topk_group
self.correction_bias = correction_bias
# 设置量化方法
if quant_config is None:
self.quant_method: Optional[QuantizeMethodBase] = UnquantizedEPMoEMethod()
self.use_fp8_w8a8 = False
self.activation_scheme = None
else:
self.quant_method: Optional[QuantizeMethodBase] = Fp8EPMoEMethod(
quant_config
)
self.use_fp8_w8a8 = True
self.fp8_dtype = torch.float8_e4m3fn
self.activation_scheme = quant_config.activation_scheme
# 创建权重
self.quant_method.create_weights(
layer=self,
num_experts_per_partition=self.num_experts_per_partition,
hidden_size=hidden_size,
intermediate_size=self.intermediate_size,
params_dtype=params_dtype,
weight_loader=self.weight_loader,
)
# 初始化分组矩阵乘法运行器
self.grouped_gemm_runner = None
这个类定义中我们可以看到它主要是做一些准备工作,同时EPMoE复用了Tensor Parallel的进程组,所以也是直接在Tensor Parallel进程组上获取当前Rank需要处理的是哪些Expert ID。
EPMoE 类的 Forward
简单添加几行注释:
def forward(self, hidden_states: torch.Tensor, router_logits: torch.Tensor):
"""前向传播函数
Args:
hidden_states: 输入的隐藏状态张量
router_logits: 路由器输出的logits张量
Returns:
output: 经过MoE层处理后的输出张量
"""
assert self.quant_method is not None
# 初始化分组矩阵乘法运行器
if self.grouped_gemm_runner is None:
self.grouped_gemm_runner = GroupedGemmRunner(
hidden_states.device, use_flashinfer=False # TODO: use flashinfer
)
# 选择专家,获取topk权重和ID
topk_weights, topk_ids = select_experts(
hidden_states=hidden_states,
router_logits=router_logits,
top_k=self.top_k,
use_grouped_topk=self.use_grouped_topk,
renormalize=self.renormalize,
topk_group=self.topk_group,
num_expert_group=self.num_expert_group,
correction_bias=self.correction_bias,
)
# 预处理topk ID,获取重排序信息
reorder_topk_ids, src2dst, seg_indptr = run_moe_ep_preproess(
topk_ids, self.num_experts
)
# 初始化门控输入张量
gateup_input = torch.empty(
(int(hidden_states.shape[0] * self.top_k), hidden_states.shape[1]),
device=hidden_states.device,
dtype=self.fp8_dtype if self.use_fp8_w8a8 else hidden_states.dtype,
)
# 动态量化时计算输入缩放因子
if self.activation_scheme == "dynamic":
max_value = (
torch.max(hidden_states)
.repeat(self.num_experts_per_partition)
.to(torch.float32)
)
self.w13_input_scale = max_value / torch.finfo(self.fp8_dtype).max
# 预重排序,重新排列输入数据
pre_reorder_triton_kernel[(hidden_states.shape[0],)](
hidden_states,
gateup_input,
src2dst,
topk_ids,
self.w13_input_scale,
self.start_expert_id,
self.end_expert_id,
self.top_k,
hidden_states.shape[1],
BLOCK_SIZE=512,
)
# 获取当前rank的分段指针和权重索引
seg_indptr_cur_rank = seg_indptr[self.start_expert_id : self.end_expert_id + 2]
weight_indices_cur_rank = torch.arange(
0,
self.num_experts_per_partition,
device=hidden_states.device,
dtype=torch.int64,
)
# 第一次分组矩阵乘法
gateup_output = torch.empty(
gateup_input.shape[0],
self.w13_weight.shape[1],
device=hidden_states.device,
dtype=hidden_states.dtype,
)
gateup_output = self.grouped_gemm_runner(
a=gateup_input,
b=self.w13_weight,
c=gateup_output,
batch_size=self.num_experts_per_partition,
weight_column_major=True,
seg_indptr=seg_indptr_cur_rank,
weight_indices=weight_indices_cur_rank,
use_fp8_w8a8=self.use_fp8_w8a8,
scale_a=self.w13_input_scale,
scale_b=self.w13_weight_scale,
)
# 激活函数处理
down_input = torch.empty(
gateup_output.shape[0],
gateup_output.shape[1] // 2,
device=gateup_output.device,
dtype=self.fp8_dtype if self.use_fp8_w8a8 else hidden_states.dtype,
)
if self.w2_input_scale is None:
self.w2_input_scale = torch.ones(
self.num_experts_per_partition,
dtype=torch.float32,
device=hidden_states.device,
)
silu_and_mul_triton_kernel[(gateup_output.shape[0],)](
gateup_output,
down_input,
gateup_output.shape[1],
reorder_topk_ids,
self.w2_input_scale,
self.start_expert_id,
self.end_expert_id,
BLOCK_SIZE=512,
)
# 第二次分组矩阵乘法
down_output = torch.empty(
down_input.shape[0],
self.w2_weight.shape[1],
device=hidden_states.device,
dtype=hidden_states.dtype,
)
down_output = self.grouped_gemm_runner(
a=down_input,
b=self.w2_weight,
c=down_output,
batch_size=self.num_experts_per_partition,
weight_column_major=True,
seg_indptr=seg_indptr_cur_rank,
weight_indices=weight_indices_cur_rank,
use_fp8_w8a8=self.use_fp8_w8a8,
scale_a=self.w2_input_scale,
scale_b=self.w2_weight_scale,
)
# 后重排序,生成最终输出
output = torch.empty_like(hidden_states)
post_reorder_triton_kernel[(hidden_states.size(0),)](
down_output,
output,
src2dst,
topk_ids,
topk_weights,
self.start_expert_id,
self.end_expert_id,
self.top_k,
hidden_states.size(1),
BLOCK_SIZE=512,
)
return output
这个forward函数的流程还是比较清晰的:
-
首先根据router_logits选择每个token要使用的top-k个专家及其权重 -
对输入数据进行预处理和重排序,将相同专家的数据分组在一起以便后续批量计算 -
执行第一次分组矩阵乘法(grouped gemm),将输入与gate和up投影权重(w13_weight)相乘 -
对第一次矩阵乘法的结果应用SiLU激活函数并进行处理 -
执行第二次分组矩阵乘法,将激活后的结果与down投影权重(w2_weight)相乘 -
最后进行后重排序,将各个专家的输出按原始token顺序重组,并根据专家权重进行加权组合得到最终输出
这个过程基本上和EP MoE训练时的步骤一致,其中第二步和最后一步就对应了EP中的两次All2All。
权重加载逻辑
笔者注:对于本篇文章的主题来说,可以不用在意这几个工具函数。
EPMoE类中还有3个和权重加载相关的函数,这里也顺便添加了注释。
@classmethod
def make_expert_params_mapping(
cls,
ckpt_gate_proj_name: str,
ckpt_down_proj_name: str,
ckpt_up_proj_name: str,
num_experts: int,
) -> List[Tuple[str, str, int, str]]:
"""生成专家参数映射关系
Args:
ckpt_gate_proj_name: 检查点中gate投影层的名称
ckpt_down_proj_name: 检查点中down投影层的名称
ckpt_up_proj_name: 检查点中up投影层的名称
num_experts: 专家总数
Returns:
List[Tuple[str, str, int, str]]: 返回参数映射列表,每个元素为元组:
- param_name: 参数名称前缀(w13或w2)
- weight_name: 权重完整名称
- expert_id: 专家ID
- shard_id: 分片ID(w1/w2/w3)
"""
return [
# (param_name, weight_name, expert_id, shard_id)
(
(
"experts.w13_"
if weight_name in [ckpt_gate_proj_name, ckpt_up_proj_name]
else "experts.w2_"
),
f"experts.{expert_id}.{weight_name}.",
expert_id,
shard_id,
)
for expert_id in range(num_experts)
for shard_id, weight_name in [
("w1", ckpt_gate_proj_name),
("w2", ckpt_down_proj_name),
("w3", ckpt_up_proj_name),
]
]
def weight_loader(
self,
param: torch.nn.Parameter,
loaded_weight: torch.Tensor,
weight_name: str,
shard_id: str,
expert_id: int,
) -> None:
"""加载权重参数
Args:
param: 目标参数
loaded_weight: 加载的权重张量
weight_name: 权重名称
shard_id: 分片ID(w1/w2/w3)
expert_id: 专家ID
Raises:
ValueError: 当shard_id不合法时抛出异常
"""
if expert_id < self.start_expert_id or expert_id > self.end_expert_id:
return
expert_id = expert_id - self.start_expert_id
if shard_id not in ("w1", "w2", "w3"):
raise ValueError(
f"shard_id must be ['w1','w2','w3'] but " f"got {shard_id}."
)
# 处理FP8缩放因子的特殊情况
if "scale" in weight_name:
self._load_fp8_scale(
param.data, loaded_weight, weight_name, shard_id, expert_id
)
return
expert_data = param.data[expert_id]
if shard_id == "w2":
param.data[expert_id] = loaded_weight
elif shard_id == "w1":
param.data[expert_id][: self.intermediate_size, :] = loaded_weight
elif shard_id == "w3":
param.data[expert_id][self.intermediate_size :, :] = loaded_weight
else:
raise ValueError(f"Expected shard_id w1,w2 or w3 but got {shard_id}")
def _load_fp8_scale(
self,
param: torch.nn.Parameter,
loaded_weight: torch.Tensor,
weight_name: str,
shard_id: str,
expert_id: int,
) -> None:
"""加载FP8量化的缩放因子
Args:
param: 目标参数
loaded_weight: 加载的权重张量
weight_name: 权重名称
shard_id: 分片ID(w1/w2/w3)
expert_id: 专家ID
Raises:
ValueError: 当输入缩放因子不相等时抛出异常
"""
param_data = param.data
# 输入缩放因子可以直接加载,且必须相等
if "input_scale" in weight_name:
if (
param_data[expert_id] != 1
and (param_data[expert_id] - loaded_weight).abs() > 1e-5
):
raise ValueError(
"input_scales of w1 and w3 of a layer "
f"must be equal. But got {param_data[expert_id]} "
f"vs. {loaded_weight}"
)
param_data[expert_id] = loaded_weight
# 权重缩放因子
elif "weight_scale" in weight_name:
# 合并列的情况(gate_up_proj)
if shard_id in ("w1", "w3"):
# 需要保留w1和w3的权重缩放因子,因为加载权重后需要重新量化
idx = 0 if shard_id == "w1" else 1
param_data[expert_id][idx] = loaded_weight
# 行并行的情况(down_proj)
else:
param_data[expert_id] = loaded_weight
这几个权重加载相关的工具函数会在模型实现中的load_weights方法中被调用,本文就不继续关注这部分了,感兴趣的读者可以查看一下VLLM和SGLang是如何优雅的做模型权重加载工作的。
解析到这里就可以了,我们把握住EPMoE类的forward的整体逻辑就行。
0x3. SGLang EP MoE Kernel实现
代码位置:https://github.com/sgl-project/sglang/blob/main/python/sglang/srt/layers/moe/ep_moe/kernels.py
再复述一次EPMoE Layer实现中的forward的主要流程,和本节要解析的kernel可以对应起来。EPMoE Layer的 forward主要流程为:
-
首先根据router_logits选择每个token要使用的top-k个专家及其权重 -
对输入数据进行预处理和重排序,将相同专家的数据分组在一起以便后续批量计算 -
执行第一次分组矩阵乘法(grouped gemm),将输入与gate和up投影权重(w13_weight)相乘 -
对第一次矩阵乘法的结果应用SiLU激活函数并进行处理 -
执行第二次分组矩阵乘法,将激活后的结果与down投影权重(w2_weight)相乘 -
最后进行后重排序,将各个专家的输出按原始token顺序重组,并根据专家权重进行加权组合得到最终输出
Token按照Expert重排index信息预处理
在 forward 函数中获得了topk_ids之后首先进行了预处理topk ID,获取重排序信息:
reorder_topk_ids, src2dst, seg_indptr = run_moe_ep_preproess(topk_ids, self.num_experts)
对应的Triton Kernel添加注释:
@triton.jit
def compute_seg_indptr_triton_kernel(reorder_topk_ids, seg_indptr, num_toks):
"""计算每个专家对应token段的起始位置
Args:
reorder_topk_ids: 排序后的专家ID
seg_indptr: 分段指针数组
num_toks: token总数
"""
# 获取当前专家ID
expert = tl.program_id(0)
# 二分查找当前专家对应的token段位置
low = 0
high = num_toks - 1
target_location = -1
while low <= high:
mid = (low + high) // 2
# 如果中间位置的专家ID大于当前专家ID,在左半部分继续查找
if tl.load(reorder_topk_ids + mid) > expert:
high = mid - 1
# 否则在右半部分继续查找,并更新目标位置
else:
low = mid + 1
target_location = mid
# 存储当前专家对应token段的结束位置
tl.store(seg_indptr + expert + 1, target_location + 1)
@triton.jit
def compute_src2dst_triton_kernel(
reorder_ids, src2dst, num_toks, BLOCK_SIZE: tl.constexpr
):
"""计算源索引到目标索引的映射
Args:
reorder_ids: 重排序后的索引
src2dst: 源索引到目标索引的映射数组
num_toks: token总数
BLOCK_SIZE: 每个线程块处理的token数量
"""
# 获取当前程序块ID
pid = tl.program_id(axis=0)
# 计算当前块内的目标索引
dst_id = pid * BLOCK_SIZE + tl.arange(0, BLOCK_SIZE)
# 生成有效token的掩码
mask = dst_id < num_toks
# 加载源索引
src_id = tl.load(reorder_ids + dst_id, mask=mask)
# 存储源索引到目标索引的映射
tl.store(src2dst + src_id, dst_id, mask=mask)
def run_moe_ep_preproess(topk_ids: torch.Tensor, num_experts: int):
"""预处理MoE专家并行的topk ID,生成重排序信息
Args:
topk_ids: 每个token选择的专家ID张量
num_experts: 专家总数
Returns:
reorder_topk_ids: 排序后的专家ID
src2dst: 源索引到目标索引的映射
seg_indptr: 每个专家对应的token段的起始位置
"""
# 对专家ID进行稳定排序
reorder_topk_ids, reorder_ids = torch.sort(topk_ids.view(-1), stable=True)
# 初始化分段指针和源目标映射数组
seg_indptr = torch.zeros(num_experts + 1, device=topk_ids.device, dtype=torch.int64)
src2dst = torch.empty(topk_ids.numel(), device=topk_ids.device, dtype=torch.int32)
# 计算每个专家对应token段的起始位置
compute_seg_indptr_triton_kernel[(num_experts,)](
reorder_topk_ids, seg_indptr, topk_ids.numel()
)
# 计算源索引到目标索引的映射
BLOCK_SIZE = 512
grid = (triton.cdiv(topk_ids.numel(), BLOCK_SIZE),)
compute_src2dst_triton_kernel[grid](
reorder_ids, src2dst, topk_ids.numel(), BLOCK_SIZE
)
return reorder_topk_ids, src2dst, seg_indptr
这段代码实际上还是比较好理解的,我这里举个例子来说明一下。
假设有10个token,4个专家(expert_id: 0,1,2,3),每个token选择的专家分配如下:
# 原始的token到专家的分配 (topk_ids)
token_idx: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
expert_ids: [1, 3, 2, 1, 0, 2, 3, 1, 2, 0]
上面代码处理后会得到:
-
排序后的专家ID (reorder_topk_ids):
[0, 0, 1, 1, 1, 2, 2, 2, 3, 3]
-
每个专家负责的token段位置 (seg_indptr):
expert_id: [0, 1, 2, 3, 4]
seg_indptr: [0, 2, 5, 8, 10]
# 含义:
# - expert 0 处理索引 0-1 的token
# - expert 1 处理索引 2-4 的token
# - expert 2 处理索引 5-7 的token
# - expert 3 处理索引 8-9 的token
-
原始位置到重排序后位置的映射 (src2dst):
原始位置: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
重排序后位置: [4, 9, 2, 3, 7, 5, 8, 6, 0, 1]
这样重排序后,相同专家要处理的token就被组织在了一起
重排序后位置: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
专家ID: [0, 0, 1, 1, 1, 2, 2, 2, 3, 3]
执行真正的Token按照Expert重排(等价于第一次All2All)
对应 EPMoE Layer forward 的下面一行代码:
pre_reorder_triton_kernel[(hidden_states.shape[0],)](
hidden_states,
gateup_input,
src2dst,
topk_ids,
self.w13_input_scale,
self.start_expert_id,
self.end_expert_id,
self.top_k,
hidden_states.shape[1],
BLOCK_SIZE=512,
)
我们看一下Triton的实现:
@triton.jit
def pre_reorder_triton_kernel(
input_ptr, # 输入张量指针
gateup_input_ptr, # 门控输入张量指针
src2dst_ptr, # 源到目标索引映射指针
topk_ids_ptr, # topk专家ID指针
a1_scales_ptr, # 输入缩放因子指针
start_expert_id, # 当前rank起始专家ID
end_expert_id, # 当前rank结束专家ID
topk, # 每个token选择的专家数量
hidden_size, # 隐藏层大小
BLOCK_SIZE: tl.constexpr, # 计算块大小
):
"""预重排序kernel,将输入数据重新排列并应用缩放
该kernel将输入数据按照专家分配重新排列,并对分配到当前rank的专家数据进行缩放处理。
对于每个输入token,遍历其选择的topk个专家,如果专家属于当前rank,则将该token的数据
拷贝到对应位置并应用缩放因子。
"""
# 获取输出数据类型
OutDtype = gateup_input_ptr.dtype.element_ty
# 获取当前处理的输入token索引
src_idx = tl.program_id(0)
# 计算当前token的src2dst和topk_ids指针位置
src2dst_ptr = src2dst_ptr + src_idx * topk
topk_ids_ptr = topk_ids_ptr + src_idx * topk
# 计算输入数据指针位置
src_ptr = input_ptr + src_idx * hidden_size
# 遍历当前token选择的topk个专家
for idx in range(topk):
# 加载专家ID
expert_id = tl.load(topk_ids_ptr + idx)
# 检查专家是否属于当前rank
if expert_id >= start_expert_id and expert_id <= end_expert_id:
# 计算缩放因子
if a1_scales_ptr is not None:
scale = 1.0 / tl.load(a1_scales_ptr + expert_id - start_expert_id)
else:
scale = 1.0
# 获取目标位置索引和指针
dst_idx = tl.load(src2dst_ptr + idx)
dst_ptr = gateup_input_ptr + dst_idx * hidden_size
# 按块处理hidden_size维度的数据
for start_offset in tl.range(0, hidden_size, BLOCK_SIZE):
offset = start_offset + tl.arange(0, BLOCK_SIZE)
mask = offset < hidden_size
# 加载输入数据并转换为float32
in_data = tl.load(src_ptr + offset, mask=mask).to(tl.float32)
# 应用缩放并转换为输出类型
out_data = (in_data * scale).to(OutDtype)
# 存储到目标位置
tl.store(dst_ptr + offset, out_data, mask=mask)
这个kernel就是根据我们上一步获得的重排信息来执行真正的重排。
Group GEMM和激活函数
接下来就是执行gateup和down的Group GEMM以及夹在它们中间的silu_and_mul激活操作。在EPMoE Forward对应的函数为:
# 获取当前rank的分段指针和权重索引
seg_indptr_cur_rank = seg_indptr[self.start_expert_id : self.end_expert_id + 2]
weight_indices_cur_rank = torch.arange(
0,
self.num_experts_per_partition,
device=hidden_states.device,
dtype=torch.int64,
)
# 第一次分组矩阵乘法
gateup_output = torch.empty(
gateup_input.shape[0],
self.w13_weight.shape[1],
device=hidden_states.device,
dtype=hidden_states.dtype,
)
gateup_output = self.grouped_gemm_runner(
a=gateup_input,
b=self.w13_weight,
c=gateup_output,
batch_size=self.num_experts_per_partition,
weight_column_major=True,
seg_indptr=seg_indptr_cur_rank,
weight_indices=weight_indices_cur_rank,
use_fp8_w8a8=self.use_fp8_w8a8,
scale_a=self.w13_input_scale,
scale_b=self.w13_weight_scale,
)
# 激活函数处理
down_input = torch.empty(
gateup_output.shape[0],
gateup_output.shape[1] // 2,
device=gateup_output.device,
dtype=self.fp8_dtype if self.use_fp8_w8a8 else hidden_states.dtype,
)
if self.w2_input_scale is None:
self.w2_input_scale = torch.ones(
self.num_experts_per_partition,
dtype=torch.float32,
device=hidden_states.device,
)
silu_and_mul_triton_kernel[(gateup_output.shape[0],)](
gateup_output,
down_input,
gateup_output.shape[1],
reorder_topk_ids,
self.w2_input_scale,
self.start_expert_id,
self.end_expert_id,
BLOCK_SIZE=512,
)
# 第二次分组矩阵乘法
down_output = torch.empty(
down_input.shape[0],
self.w2_weight.shape[1],
device=hidden_states.device,
dtype=hidden_states.dtype,
)
down_output = self.grouped_gemm_runner(
a=down_input,
b=self.w2_weight,
c=down_output,
batch_size=self.num_experts_per_partition,
weight_column_major=True,
seg_indptr=seg_indptr_cur_rank,
weight_indices=weight_indices_cur_rank,
use_fp8_w8a8=self.use_fp8_w8a8,
scale_a=self.w2_input_scale,
scale_b=self.w2_weight_scale,
)
Group GEMM和激活函数都是比较常规的,这里就不解析这两个比较长的Triton实现了,使用Triton来实现这两个操作也是相当不高效的。
后重排序(等价于第二次All2All),生成最终输出
对应了EPMoE的最后2行代码:
output = torch.empty_like(hidden_states)
post_reorder_triton_kernel[(hidden_states.size(0),)](
down_output,
output,
src2dst,
topk_ids,
topk_weights,
self.start_expert_id,
self.end_expert_id,
self.top_k,
hidden_states.size(1),
BLOCK_SIZE=512,
)
Triton Kernel代码如下:
@triton.jit
def post_reorder_triton_kernel(
down_output_ptr # 存储专家处理后的输出
output_ptr # 最终输出结果的存储位置
src2dst_ptr # 重排序映射关系
topk_ids_ptr # 每个token对应的专家ID
topk_weights_ptr # 每个token对应的专家权重
start_expert_id, # 起始专家ID
end_expert_id, # 结束专家ID
topk, # topk值
hidden_size, # 隐藏层大小
BLOCK_SIZE: tl.constexpr, # 块大小常量
):
"""后重排序triton核函数
该函数将专家输出重新排序并加权求和,生成最终输出。
主要步骤:
1. 获取输入数据类型和程序ID
2. 计算各指针偏移量
3. 对每个block:
- 创建零向量用于累加
- 对每个topk专家:
* 如果专家ID在范围内,加载并累加其输出
4. 如果没有计算过的专家,输出全零向量
"""
# 获取输入数据类型
InDtype = down_output_ptr.dtype.element_ty
# 获取当前程序ID作为源索引
src_idx = tl.program_id(0)
# 计算各指针的实际位置
src2dst_ptr = src2dst_ptr + src_idx * topk
topk_ids_ptr = topk_ids_ptr + src_idx * topk
topk_weights_ptr = topk_weights_ptr + src_idx * topk
# 标记是否有专家参与计算
computed = False
# 计算存储位置
store_ptr = output_ptr + src_idx * hidden_size
# 按block大小遍历hidden_size
for start_offset in tl.range(0, hidden_size, BLOCK_SIZE):
offset = start_offset + tl.arange(0, BLOCK_SIZE)
mask = offset < hidden_size
# 创建零向量用于累加
sum_vec = tl.zeros([BLOCK_SIZE], dtype=InDtype)
# 遍历topk个专家
for idx in range(topk):
expert_id = tl.load(topk_ids_ptr + idx)
# 检查专家ID是否在有效范围内
if expert_id >= start_expert_id and expert_id <= end_expert_id:
computed = True
# 加载目标索引和权重
dst_idx = tl.load(src2dst_ptr + idx)
weigh_scale = tl.load(topk_weights_ptr + idx).to(InDtype)
# 计算加载位置并加载数据
load_ptr = down_output_ptr + dst_idx * hidden_size
in_data = tl.load(load_ptr + offset, mask=mask)
# 加权累加
sum_vec += in_data * weigh_scale
# 存储累加结果
tl.store(store_ptr + offset, sum_vec, mask=mask)
# 如果没有专家参与计算,输出全零
if computed == False:
for start_offset in tl.range(0, hidden_size, BLOCK_SIZE):
offset = start_offset + tl.arange(0, BLOCK_SIZE)
mask = offset < hidden_size
tl.store(
store_ptr + offset, tl.zeros([BLOCK_SIZE], dtype=InDtype), mask=mask
)
只看这个代码可能还是有点抽象,我继续用上面的Token按照Expert重排index的例子来说明下,我新增一组expert_weights:
注意,每个token有topk个权重,也就是select_experts输出的topk_weights。
# 原始的token分配和权重
token_idx: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
expert_ids: [1, 3, 2, 1, 0, 2, 3, 1, 2, 0]
expert_weights: [0.6,0.8,0.7,0.5,0.9,0.6,0.7,0.4,0.8,0.5]
# 重排序后的顺序(之前例子的结果)
重排序位置: [0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
专家ID: [0, 0, 1, 1, 1, 2, 2, 2, 3, 3]
现在,post_reorder_triton_kernel kernel的工作流程是:
-
对每个原始token位置(通过src_idx = tl.program_id(0)获取):
# 比如处理原始token_idx=0的数据时:
expert_id = 1
weight = 0.6
# 需要从重排序后的位置2,3,4中找到对应的输出结果
也就是下面这行代码:
src2dst_ptr = src2dst_ptr + src_idx * topk
-
处理hidden_size维度的数据:
假设hidden_size=1024,BLOCK_SIZE=256,代码会将1024维的数据分成4个块来处理,每个块创建一个零向量用于累加结果
-
对每个token的专家输出进行加权组合:
# 以token_idx=0为例:
sum_vec = 0 # 初始化累加向量
expert_output = load_expert_output(expert_id=1) # 加载专家1的输出
sum_vec += expert_output * 0.6 # 应用权重0.6
-
如果当前token有专家处理(computed=True),存储加权后的结果,否则存储全零向量。
通过这个后重排序,我们就可以支持一个token被多个专家并行处理以及使用topk weights来控制不同专家的贡献程度。
0x4. SGLang EPMoE 和 MoE EP训练流程的区别
回收开头,EPMoE Layer forward的最后为什么要对结果使用tensor_model_parallel_all_reduce?
实际上从上面的EPMoE Forward的流程来看,我么们发现它是直接实现了几个Triton Kernel来等价原始的Expert Parallel中的2次All2All,并没有像训练那样调用通信源语来做All2All。然后从上面的post_reorder_triton_kernel中对每个token的累加过程来看,如果某个Rank上的当前token没有被这个Rank持有的Expert处理的话,它的输出会设置为0,但是如果在另外一个EP Rank上对当前这个token是会被它持有的Expert处理的话,我们最终就需要做一次allreduce把所有rank上的结果加起来。在推理的时候All2All几乎没有重叠机会,而All2All的速度是比较慢的,通过这里的对All2All流程的优化其实也可以降低通信的成本。
0x5. 总结
SGLang EPMoE目前这个实现整体上比较清晰,但笔者目前没有详细实测过这个Feature,所以不确定它和普通的TP的性能谁更好,此外这个EPMoE计算流程中最耗时的Group GEMM也暂时没有使用FalshInfer的优化版本,Triton的实现应该会比较慢。
(文:GiantPandaCV)

