摘要

我们提出了GVPO，优势:(1)唯一最优解恰好是KL约束的reward最大化最优解(2)支持多样化采样分布，避免on-policy和重要性采样带来的各种问题。

随着Deepseek的火爆，其中用到的强化学习算法GRPO也引起了广泛关注。GRPO通过对每一个prompt多次采样，避免了额外训练value model的开销。尽管如此，实践中复现GRPO经常表现出训练不稳定、效果表现不佳等症状。为此我们提出了GVPO(Group Variance Policy Optimization), 可以无缝适配现有GRPO框架并取得更好的表现、更稳定的训练并支持更丰富的数据来源。

动机

受到DPO的启发，我们也希望在GRPO场景(每个prompt多次采样)下利用KL约束的reward最大化

的解析解形式：

然而这里有一个问题在于公式里的Z(x)是对所有可能y的期望，在实践中难以计算。为此，我们发现当一个prompt内所有采样的梯度系数加和为0时，Z(x)可以被消掉。

即对于

当

GVPO

受此启发，我们提出了GVPO：

其中

我们证明GVPO具有非常好的物理性质。具体来说

第一步是因为  可以被消掉。第二步是因为  。第三步是因为  。

由此可见，GVPO居然本质是一个MSE loss！(喜）其中  是MSE的预测值，  是MSE的真实值。

理论保证

基于这个变形，我们很容易（注意到.jpg）证明GVPO的理论最优解恰好是KL约束的reward最大化的最优解，即  。

定理1

最小化  的唯一policy是  ，其中

这个定理保证了GVPO实践中的有效性和稳定性。

上式中 y 是依惯例从要对齐的policy  中采样，在实践中即 或 。我们接下来可以证明，GVPO支持从更广泛的分布中采样，且依然保持最优解性质。

定理2

最小化  的唯一policy是  ，其中

对于满足  的任意  都成立。

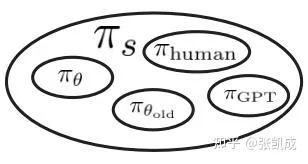
在实践中由softmax decoding的policy都满足这个定理的要求。这意味着，GVPO支持非常广泛的采样分布：

接下来我们正式展示GVPO的算法流程：

注意到GVPO的每个step中，  对齐的都是上一个step的policy  。我们还证明了，GVPO在n步结束后，依然能够对齐最初的policy:

定理3

使用  的n步算法——从  开始，在第t步更新时设置  ——最大化了如下目标

定理3可以保证GVPO的每一步更新都是稳定的（因为具有一个大约束  ），且最终优化可以“走得更远”（最终对齐的是  ）。

除此之外，文章中还证明了采样得到的loss是  的无偏一致估计量，进一步保证了算法的性能。

与DPO的比较

GVPO与DPO一样，都利用到了KL约束的reward最大化的解析解。DPO是利用BT模型，两两相减消去了不可计算的 Z(x) 。而GVPO则是利用了  的性质而适用于多response的情况。这两个算法利用解析解带来了两个好处：

• • 保证了算法优化过程的稳定性，  不会过分偏离 
• • 将一个同时有policy  和reward R 的复杂优化，简化成了只有reward R 和  的简单优化。

除此之外，GVPO和DPO相比还有一个重要的理论优势。DPO其实不一定具有唯一的最优解，换句话说KL约束的reward最大化的解可能只是DPO众多最优解中的一个。这源于DPO依赖的BT模型的内生缺陷。这个问题会导致，优化DPO目标不一定会随之优化我们真实想要的目标（即KL约束的reward最大化）。而GVPO则由定理1证明了其唯一解的性质。

与GRPO及Policy Gradient Methods比较

我们先比较GVPO与其余算法的结构相似性。为了简洁我们在这一节假设  。我们将  展开并稍作变换可以得到其在梯度上等价于

其中

可以发现GVPO的loss里一共有三项：

• •  鼓励了最大化advantage。这在GRPO里的对应是标准化分数后的rewards。
• •  限制了  不能过分偏离  ，对应于  。此外，在GVPO算法实现里设置了  ，实际上对应了PPO和TRPO的trust-region限制，这保证了policy在更新过程中的稳定性。
• •  平衡了探索exploration与利用exploitation。这一项对应于熵正则  。增加熵鼓励更多的探索性，分布会趋于均匀分布。但可能会限制高质量response的概率。反之，减少熵加速了收敛，但会在多样性上带来问题。因此，实践中如何决定熵正则的系数十分困难和敏感。而  先天的支持将低质量的response概率为0而高质量的response概率尽可能接近。即概率分布可以呈现蛋糕状(cake is not a lie!)。

我们进一步比较GVPO和Policy Gradient Methods更深层次的区别。实践中，Policy Gradient Methods为了保证更新的稳定性，会在最大化reward的过程中使用KL散度的惩罚限制  偏离  的程度，即：

这带来一个问题，即必须从当前的policy  中采样，带来低采样效率的问题。作为一种解决方式，可以引入重要性采样：

重要性采用使得可以从之前的policy  中采样。然而其中带来了重要性采样系数  ，当  和  差别较大时会带来梯度爆炸或者梯度消失等问题。PPO和GRPO等算法在实践中采用了clip技术，强制限制重要性采样系数不要过大或过小。但因此，clip会导致无偏性消失并带来各种各样的问题。

作为对比，GVPO就没有这些问题，因为GVPO从一开始就不需要on- policy采样。将上述Policy Gradient Methods内减去一个常数可以得到：

作为对比，GVPO的梯度是：

由此可见带KL约束的Policy Gradient Methods其实是GVPO当  的一种特例！这也体现出GVPO能将采样分布  解耦带来的优势：一方面避免了on-policy样本利用率低的缺点，另一方面也避免了现有off-policy方法的重要性采样带来的缺点。

总结

本文的封面概括了GVPO的核心内容：

• • 蓝色部分。我们从梯度权重 w 出发设计了GVPO loss，通过与policy gradient对比，体现了GVPO具有采样丰富性的优势。
• • 红色部分。GVPO可以表示成真实reward和隐式reward的MSE形式。从MSE形式可以进一步推导出GVPO理论唯一最优解的优良性质。
• • 黄色部分。通过拆解GVPO loss，可以从正则项的角度说明GVPO的稳定性。

此外，GVPO的实现十分简单，文章中展示了在verl框架下如何只修改几行代码实现GVPO。

论文：GVPO: Group Variance Policy Optimization for Large Language Model Post-Training
链接：https://arxiv.org/abs/2504.19599

感谢熊辉教授，洪定乾老师和各位合作者对本工作的支持。

欢迎讨论:-)